Основные тригонометрические тождества

1. Основные тригонометрические тождества Домашнее задание 1. знать определение всех функций, выучить тригонометрические тождества

2. в тетради решение 3 задач из
презентации (классная работа)
3. Формулы для вычисления
координат точки (выучить)
1

2.

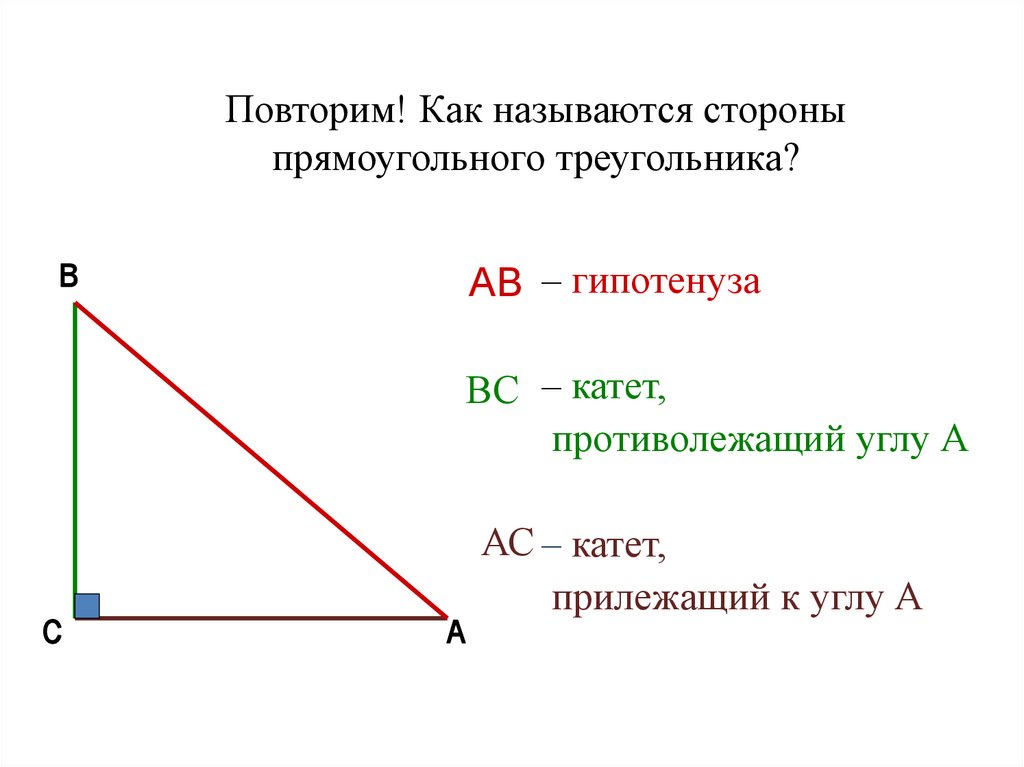
Повторим! Как называются стороны
прямоугольного треугольника?
В
AB – гипотенуза
ВС – катет,
противолежащий углу А
С
А
АС – катет,
прилежащий к углу А

3.

1.Синусом острого угла
прямоугольного треугольника
называется
-отношение противолежащего
катета к гипотенузе.
B
C
А

4.

2.Косинусом острого угла
прямоугольного треугольника
называется
-отношение прилежащего катета
к гипотенузе.
B
C
А

5.

B
3.Тангенсом острого угла
прямоугольного треугольника
называется
C
-отношение противолежащего катета
к прилежащему
А

6.

B
4.Котангенсом острого угла
прямоугольного треугольника
называется
C
- отношение прилежащего катета к
противолежащему катету
А

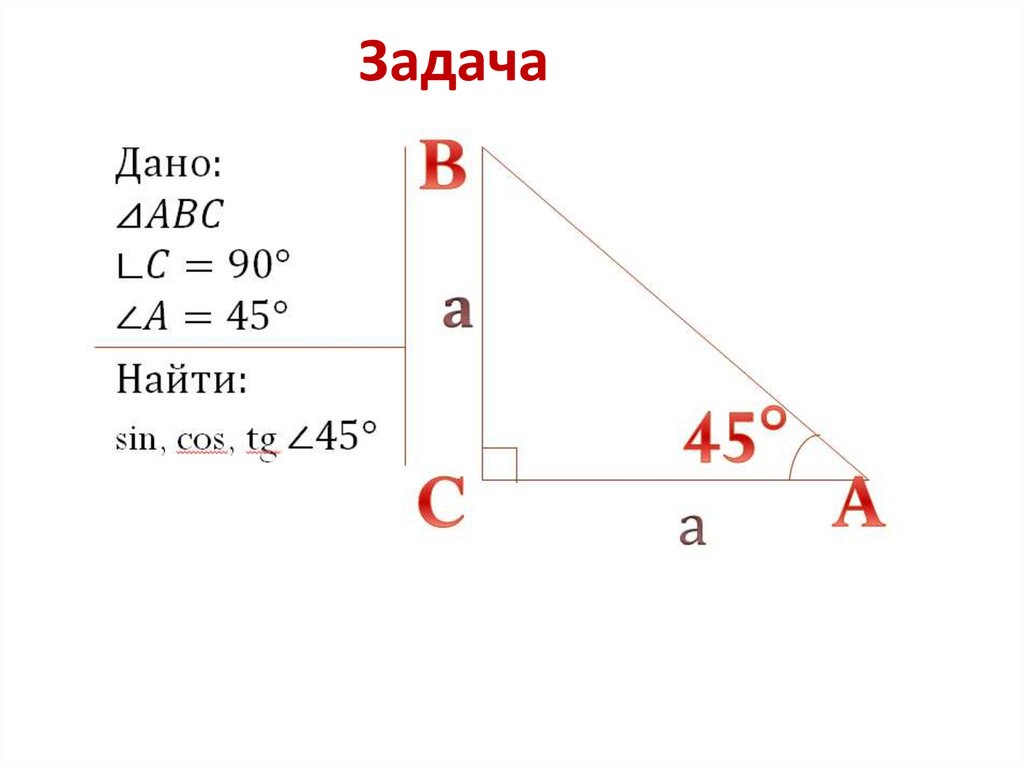
7. Задача

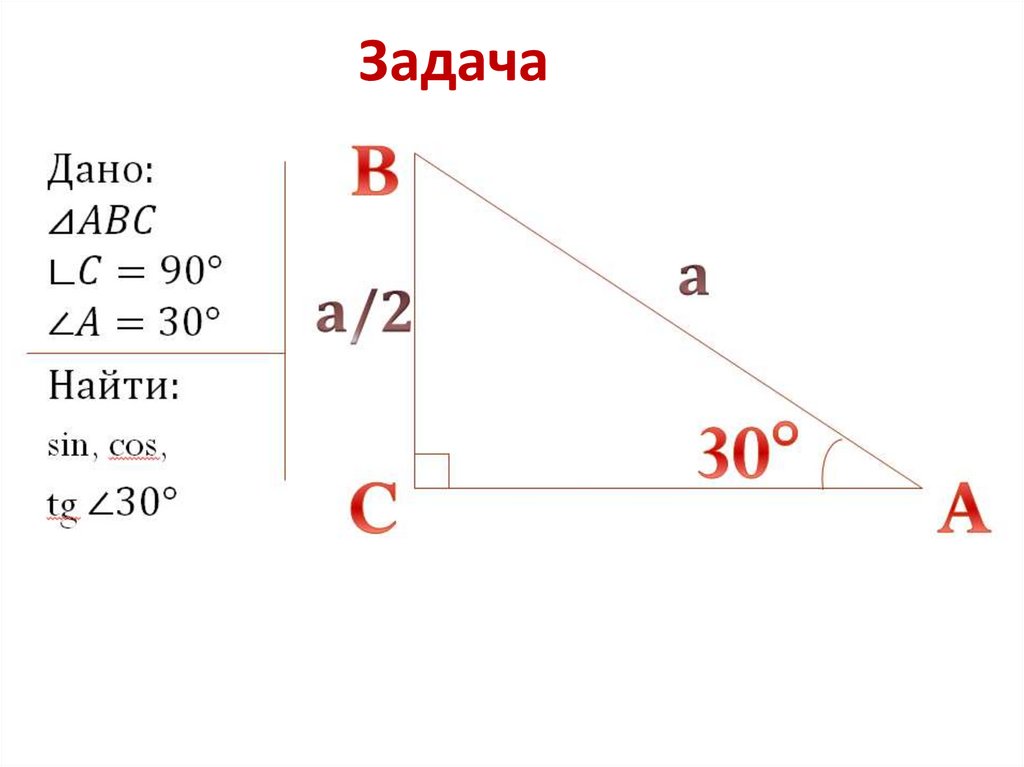
8. Задача

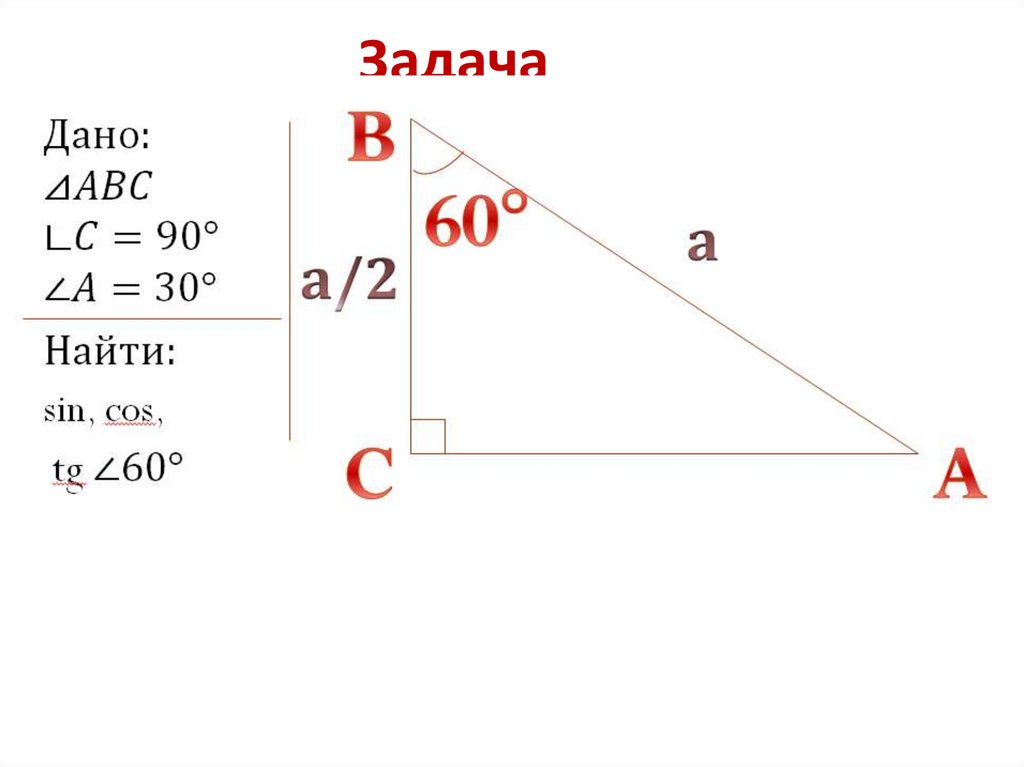
9. Задача

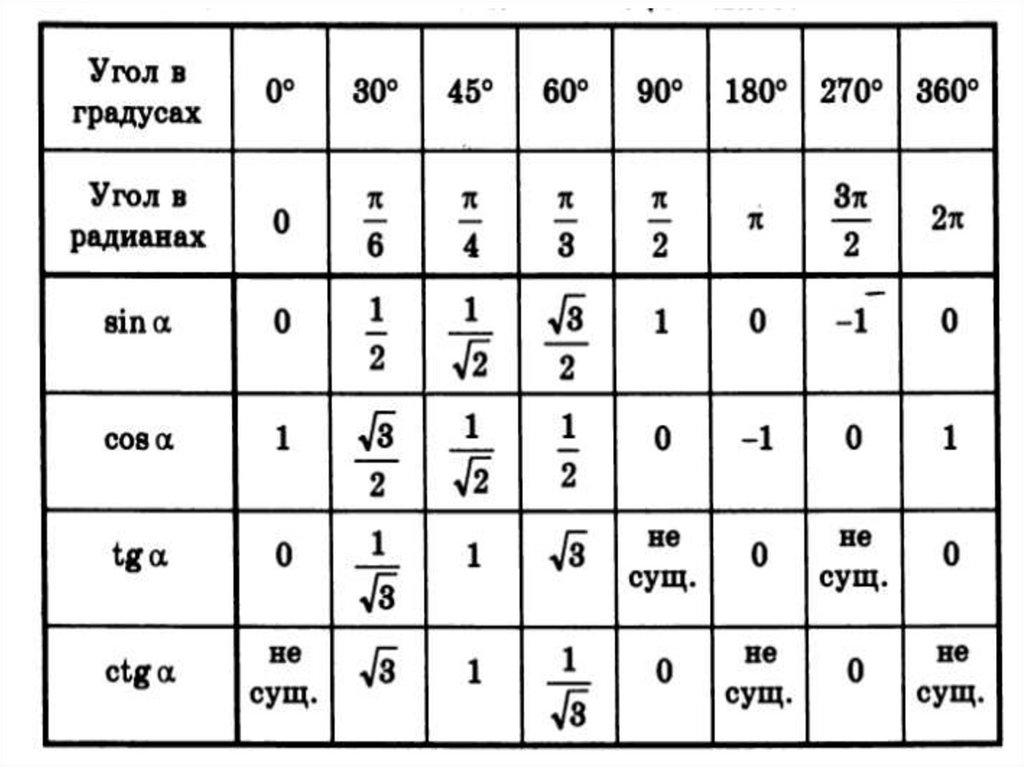
10.

11. Теорема о формулах приведения

12. Основные тригонометрические тождества

tga
sin a
cos a
сtga
cos a
sin a

13. Основные тригонометрические тождества

1
tg a 1
2
cos a
2
1
2
ctg a 1
2
sin a

14.

Равенство называется
основным тригонометрическим
тождеством
2
2
sin a cos a 1
14

15.

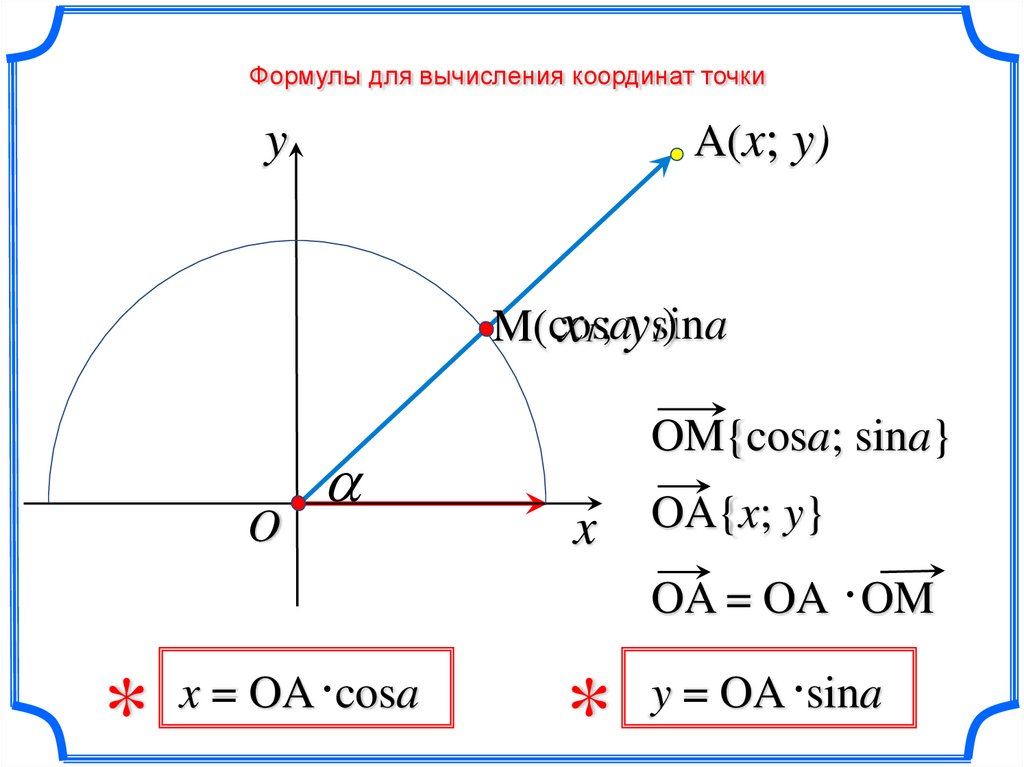
Формулы для вычисления координат точки
y
A(x; y)
)
M(cosa
x1 ; y1sina
O
*
x = OA cosa
OM{cosa; sina}
x
*
OA{x; y}
OA = OA OM
y = OA sina