Тригонометрические функции острого и тупого углов

1. Тригонометрические функции острого и тупого углов

Тригонометрические функции острого угла

2.

3. Определение

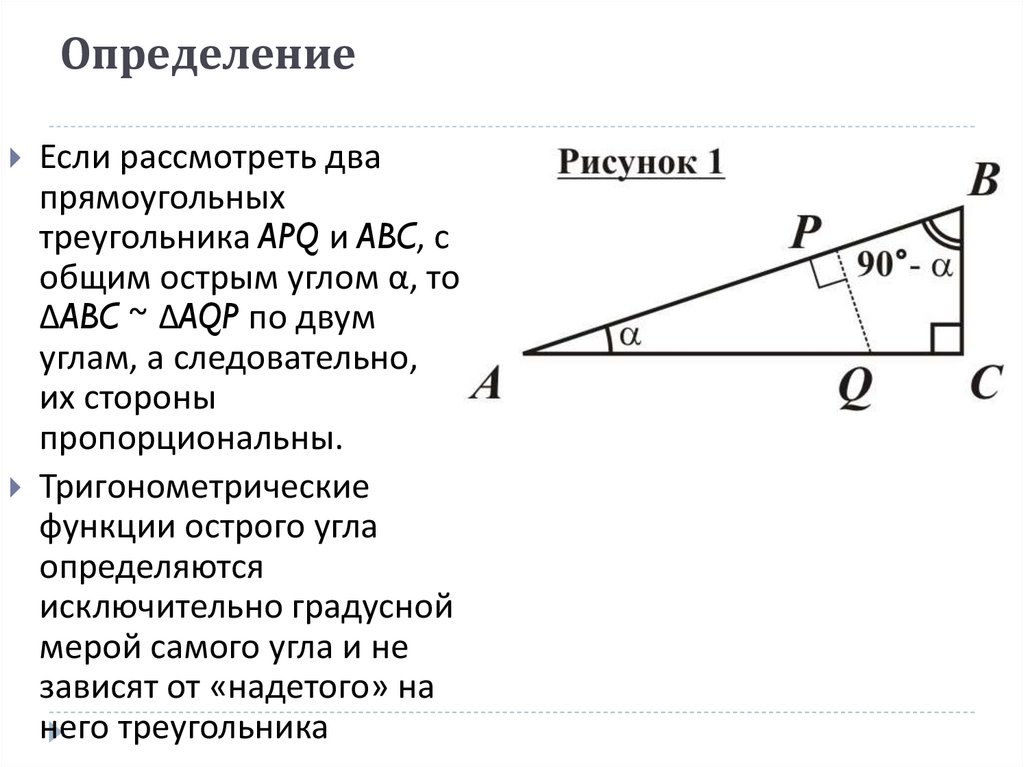
Если рассмотреть два
прямоугольных
треугольника APQ и ABC, с
общим острым углом α, то
ΔABC ~ ΔAQP по двум
углам, а следовательно,
их стороны
пропорциональны.
Тригонометрические
функции острого угла
определяются
исключительно градусной
мерой самого угла и не
зависят от «надетого» на
него треугольника

4. Определение

Синусом острого угла прямоугольного
треугольника ABC называется отношение
противолежащего катета к гипотенузе
BC
sin
AB
Косинусом острого угла прямоугольного
треугольника ABC называется отношение
прилежащего катета к гипотенузе
AC
cos
AB

5. Определение

Тангенсом острого угла прямоугольного
треугольника ABC называется отношение
противолежащего катета к прилежащему
BC
tg
AC
Котангенсом острого угла прямоугольного
треугольника ABC называется отношение
прилежащего катета к противолежащему
AC
ctg
BC

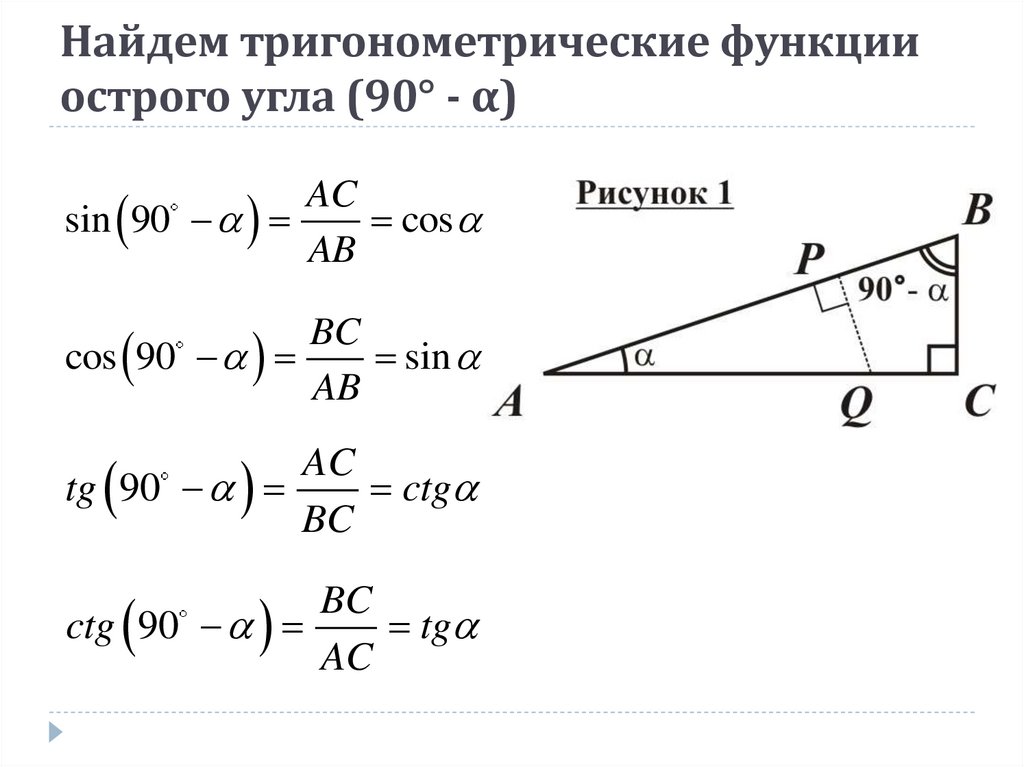
6. Найдем тригонометрические функции острого угла (90° ‑ α)

Найдем тригонометрические функции
острого угла (90° - α)
AC
sin 90
cos
AB
BC
cos 90
sin
AB
AC
tg 90
ctg
BC
BC
ctg 90
tg
AC

7. «СИНУС»

Слово встречается в индийских трудах IV-V вв.
Линия синуса называлась «джива» – тетива лука.
Позднее термин был переделан в «джаб». При
переводе с арабского на латынь употребили слово
sinus – дословный перевод слово «джайб».
Для обозначения синуса использовались
различные сокращения. Современное
обозначение sin закрепилось в 18 веке (Симпсон,
Эйлер, Д’аламбер, Лагранж), чему способствовал
авторитет Эйлера, который перенял обозначения
от И. Бернулли.

8.

«КОСИНУС». Сокращение выражения complementi sinus
– «дополнительный синус». В трудах арабских
математиков косинус рассматривался как синус
дополнения угла до 90° (18 в.).
«ТАНГЕНС». Тангенс и котангенс фигурировали в науке
о солнечных часах у арабских математиков. В работах
известного математика Ал-Хорезми (9 в.) приведены
таблицы тангенсов и котангенсов. «Тангенс»
происходит от латинского tangere – «касаться» (Финке,
1583)
«КОТАНГЕНС». Котангенсы появились раньше тангенсов
(арабские математики, 9 в.)

9. Тригонометрические тождества

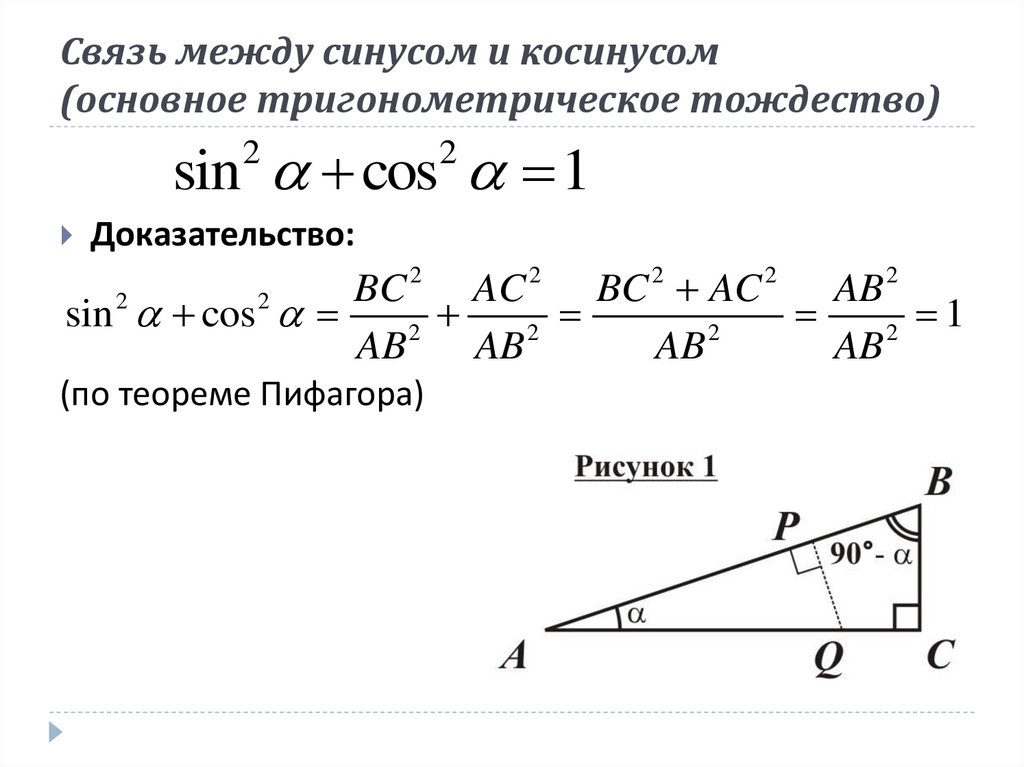
С доказательством

10. Связь между синусом и косинусом (основное тригонометрическое тождество)

sin cos 1
2
2
Доказательство:
BC
AC
BC AC
AB
sin cos
1
2
2
2
2
AB
AB
AB
AB
2
2
2
(по теореме Пифагора)
2
2
2
2

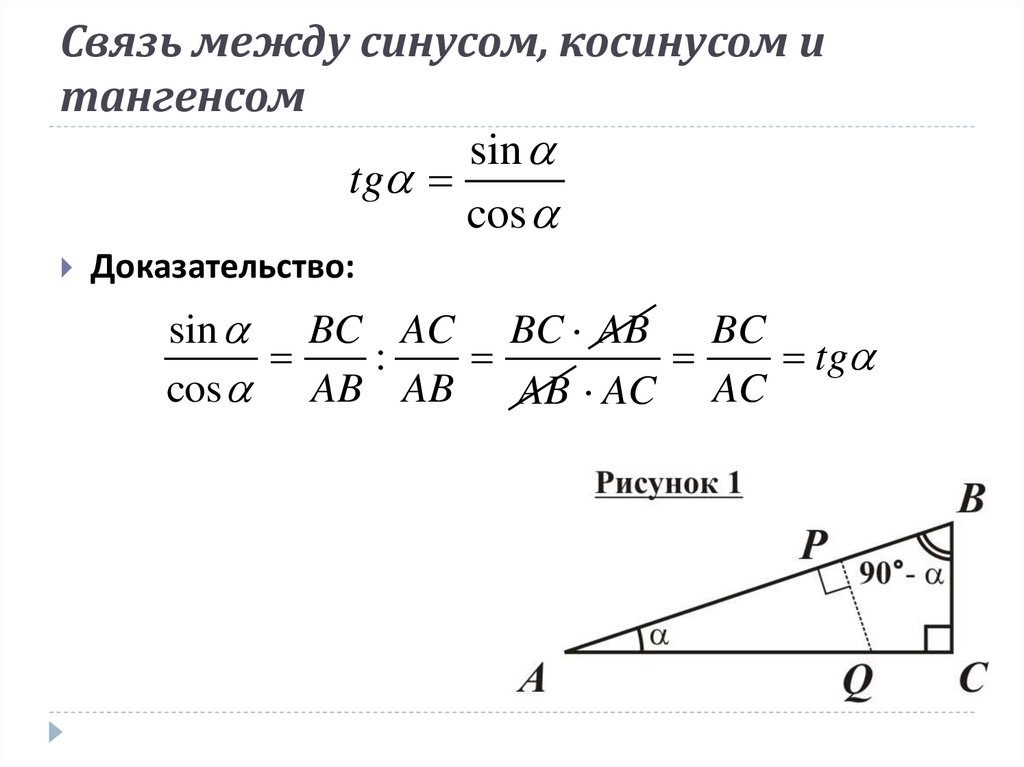
11. Связь между синусом, косинусом и тангенсом

sin
tg
cos
Доказательство:
sin BC AC BC AB BC
:
tg
cos AB AB
AB AC AC

12. Связь между синусом, косинусом и котангенсом

cos
ctg
sin
Доказательство:
cos AC BC AC AB AC
:
ctg
sin
AB AB
AB BC BC

13. Связь между тангенсом и котангенсом

tg ctg 1
Доказательство:
BC AC
tg ctg
1
AC BC

14. Связь между тангенсом и косинусом

1
1 tg
2
cos
2
Доказательство:
Разделим обе части основного тригонометрического
тождества на cos2 0
sin cos
sin cos 1 : cos 0
2
2
cos cos c
1
1
2
tg 1
2
2
cos
cos
2
2
2
2
2

15. Связь между котангенсом и синусом

1
1 ctg
2
sin
2
Доказательство:
Разделим обе части основного тригонометрического
тождества на sin 2 0
2
2
sin
cos
1
2
2
2
sin cos 1 : sin 0 2
2
2
sin sin sin
1
1 ctg
2
sin
2

16. Значения тригонометрических функций углов в 30°, 45° и 60°.

Рассмотрим прямоугольный треугольник с острыми
углами в 30° и 60° и меньшим катетом, равным 1.
По свойству прямоугольного треугольника с углом в
30°, AB = 2. Катет AC найдем по теореме Пифагора:
AC AB BC 4 1 3
2
2
Найдем тригонометрические функции углов в 30° и
60°:

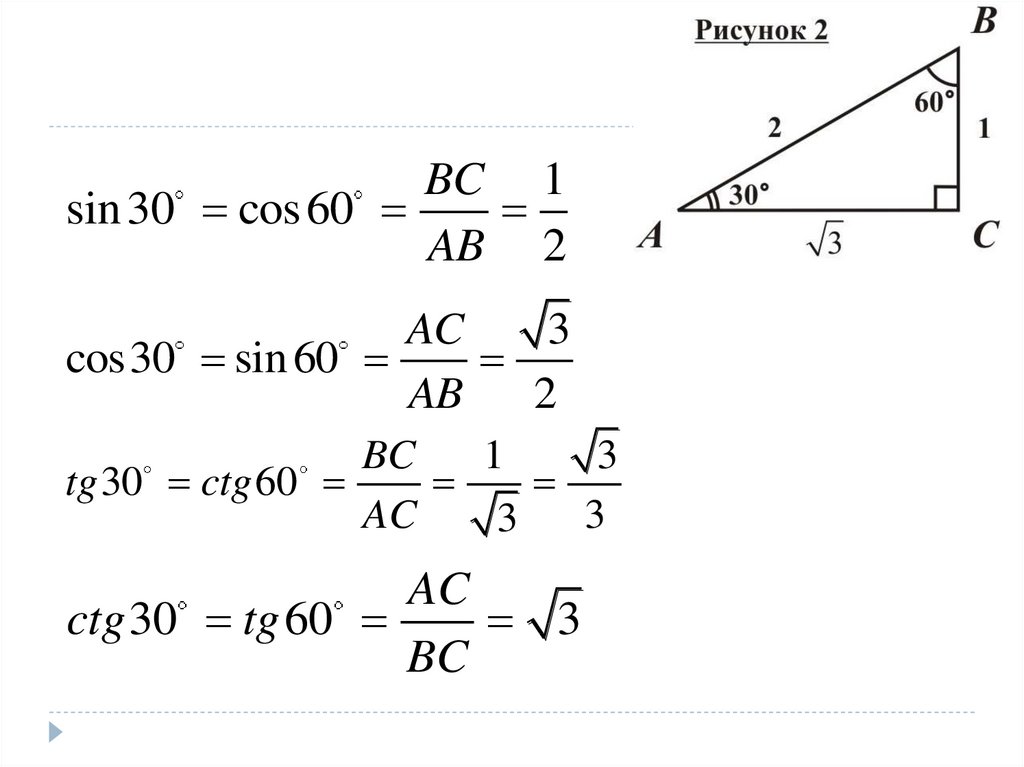
17.

BC 1
sin 30 cos 60
AB 2
AC
3
cos30 sin 60
AB
2
BC
1
3
tg 30 ctg 60
AC
3
3
AC
ctg 30 tg 60
3
BC

18.

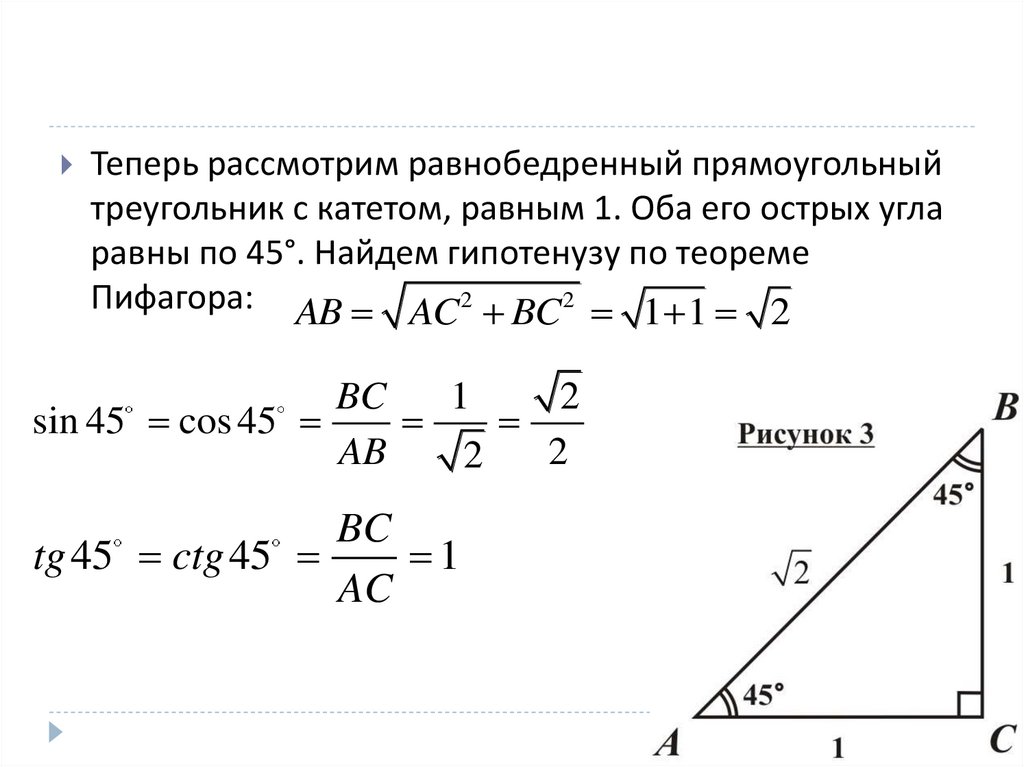
Теперь рассмотрим равнобедренный прямоугольный
треугольник с катетом, равным 1. Оба его острых угла
равны по 45°. Найдем гипотенузу по теореме
Пифагора: AB AC 2 BC 2 1 1 2
BC
1
2
sin 45 cos 45
AB
2
2
BC
tg 45 ctg 45
1
AC

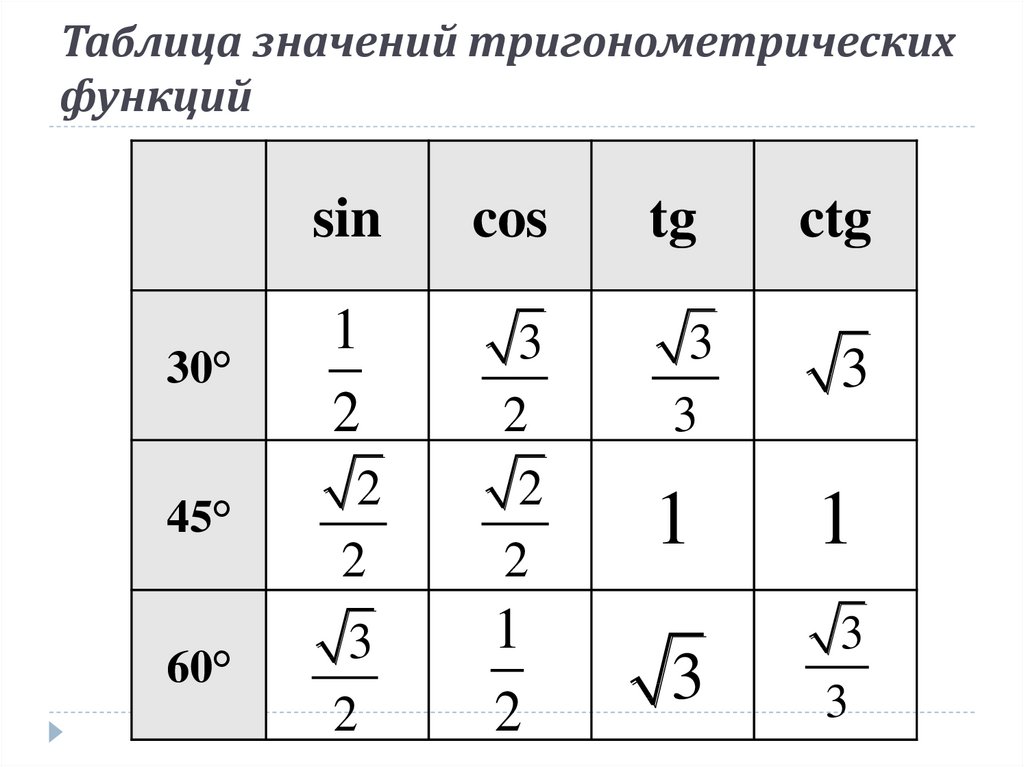
19. Таблица значений тригонометрических функций

sin
cos
30°
1
2
45°
2
2
3
2
2
2
60°
3
2
1
2
tg
3
3
ctg
3
1
1
3
3
3