Степенная функция

1.

12.03.2025

2.

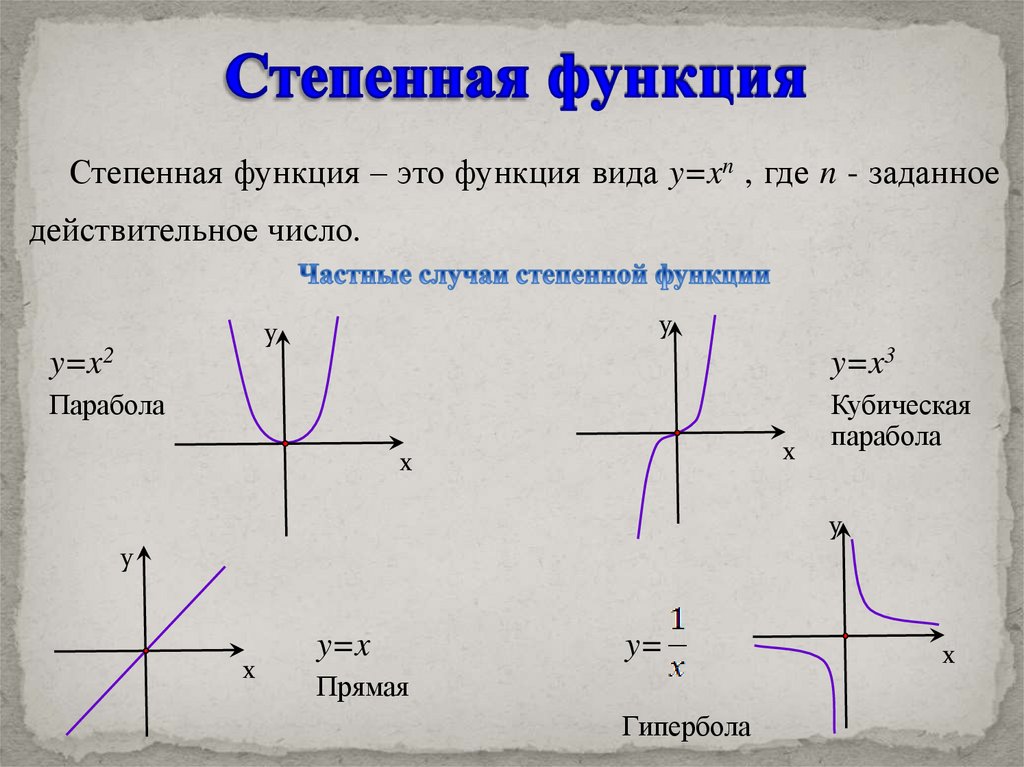
Степенная функция – это функция вида y=xn , где n - заданное
действительное число.
у
у
y=x2
y=x3
Парабола
Кубическая
парабола
х
х
у
у
х
y=x
y=
Прямая
Гипербола
х

3.

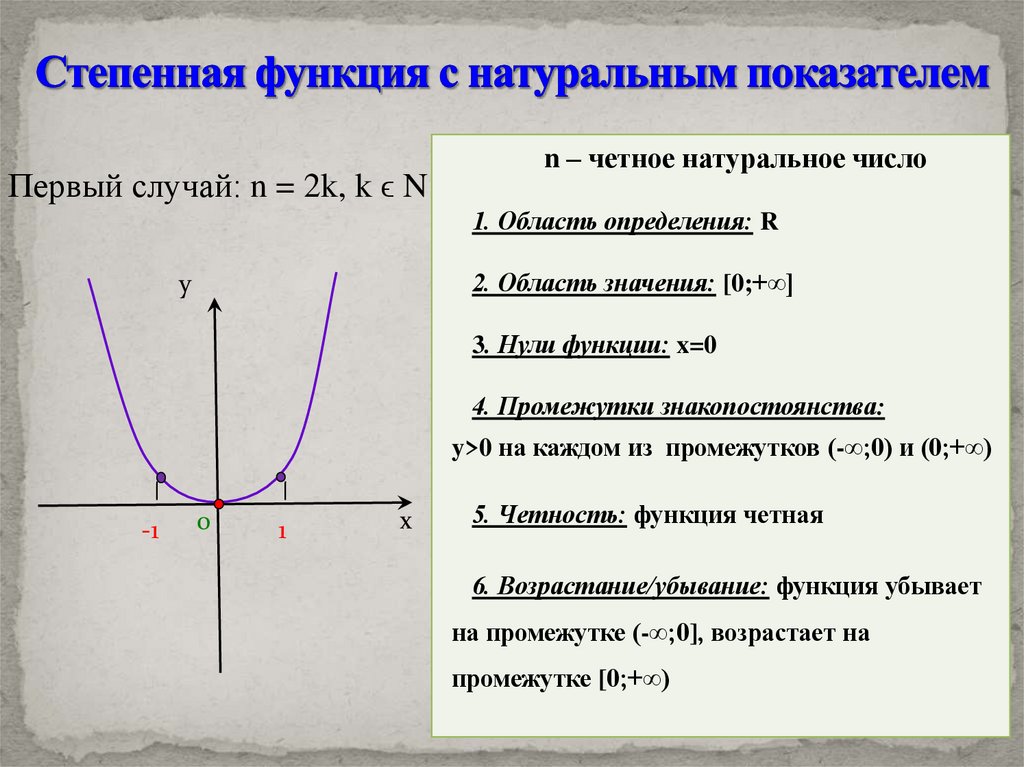
Первый случай: n = 2k, k ϵ N
n – четное натуральное число
1. Область определения: R
2. Область значения: [0;+∞]
у
3. Нули функции: x=0
4. Промежутки знакопостоянства:
y>0 на каждом из промежутков (-∞;0) и (0;+∞)
-1
0
1
х
5. Четность: функция четная
6. Возрастание/убывание: функция убывает
на промежутке (-∞;0], возрастает на
промежутке [0;+∞)

4.

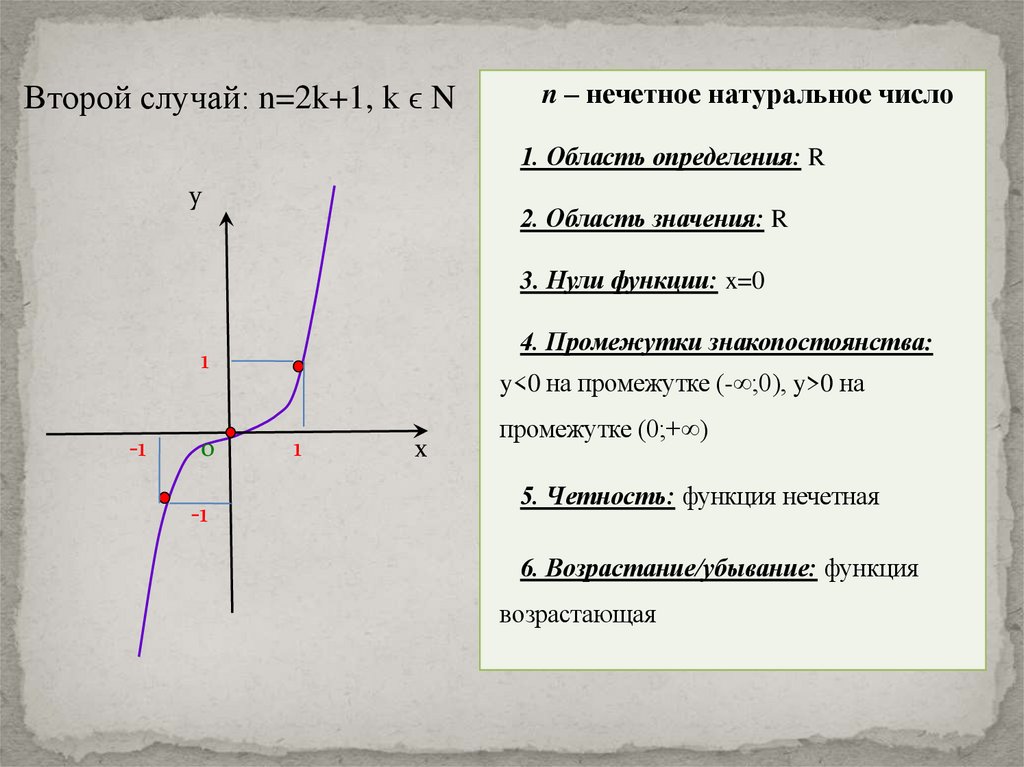
Второй случай: n=2k+1, k ϵ N
n – нечетное натуральное число
1. Область определения: R
у
2. Область значения: R
3. Нули функции: x=0
4. Промежутки знакопостоянства:
1
-1
0
-1
y<0 на промежутке (-∞;0), y>0 на
1
х
промежутке (0;+∞)
5. Четность: функция нечетная
6. Возрастание/убывание: функция
возрастающая

5.

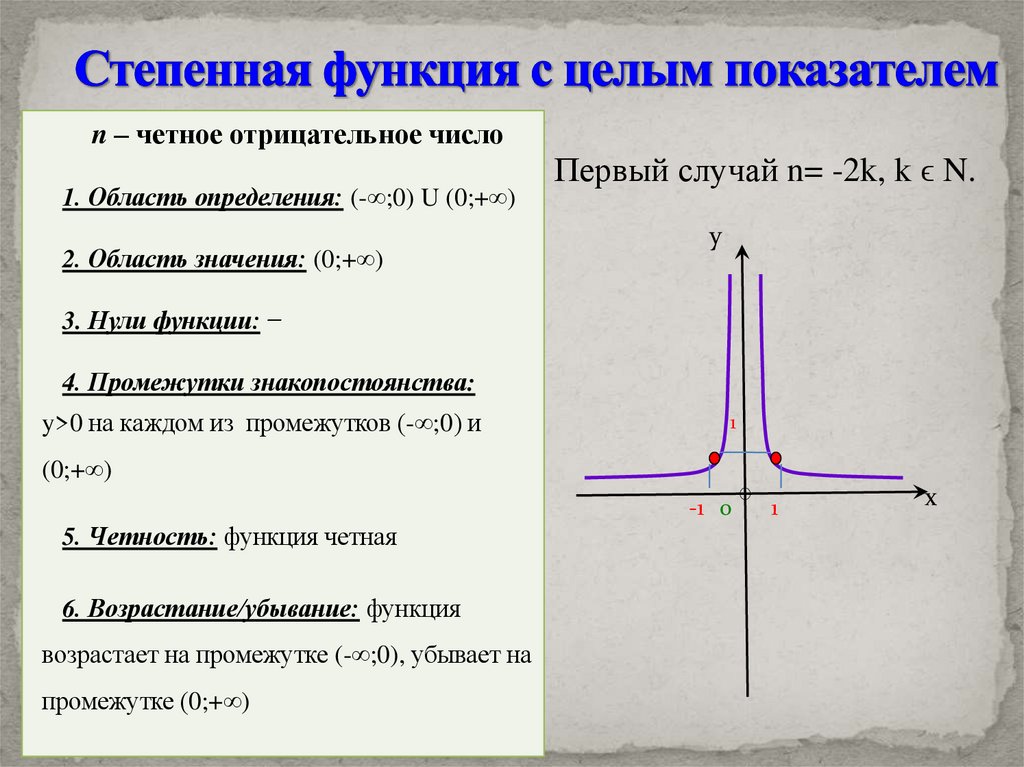
n – четное отрицательное число
1. Область определения: (-∞;0) U (0;+∞)
2. Область значения: (0;+∞)
Первый случай n= -2k, k ϵ N.
у
3. Нули функции: ̶
4. Промежутки знакопостоянства:
y>0 на каждом из промежутков (-∞;0) и
1
(0;+∞)
-1 0
5. Четность: функция четная
6. Возрастание/убывание: функция
возрастает на промежутке (-∞;0), убывает на
промежутке (0;+∞)
1
х

6.

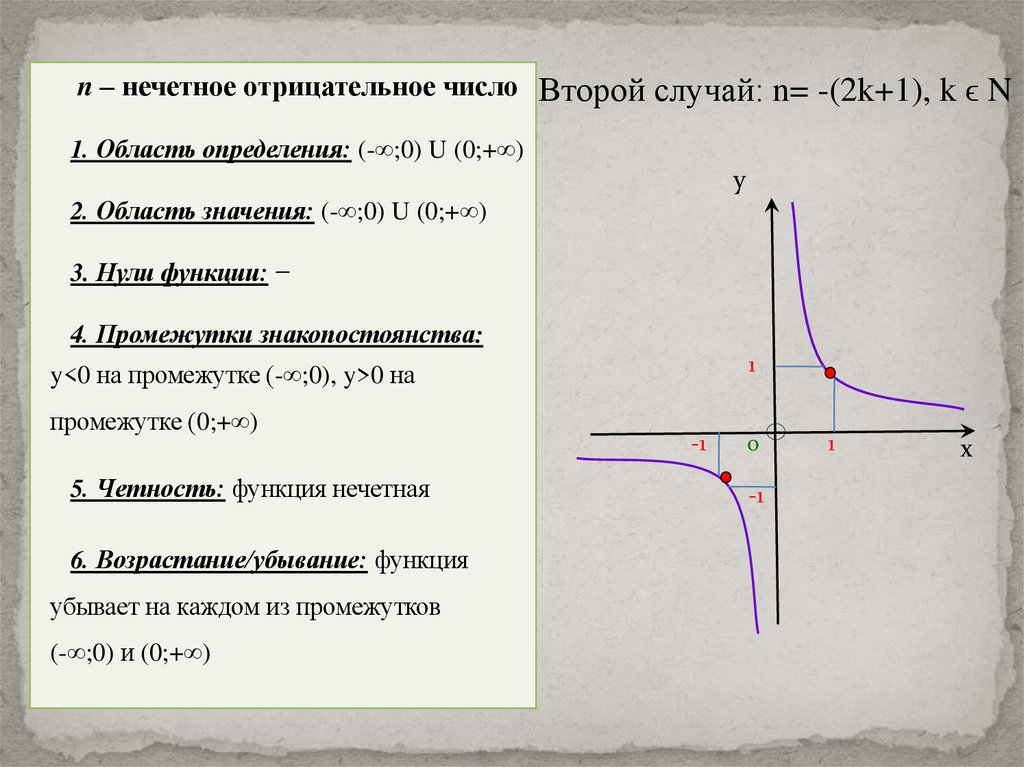
n – нечетное отрицательное число Второй случай: n= -(2k+1), k ϵ N
1. Область определения: (-∞;0) U (0;+∞)
у
2. Область значения: (-∞;0) U (0;+∞)
3. Нули функции: ̶
4. Промежутки знакопостоянства:
1
y<0 на промежутке (-∞;0), y>0 на
промежутке (0;+∞)
5. Четность: функция нечетная
6. Возрастание/убывание: функция
убывает на каждом из промежутков
(-∞;0) и (0;+∞)
-1
0
-1
1
х

7.

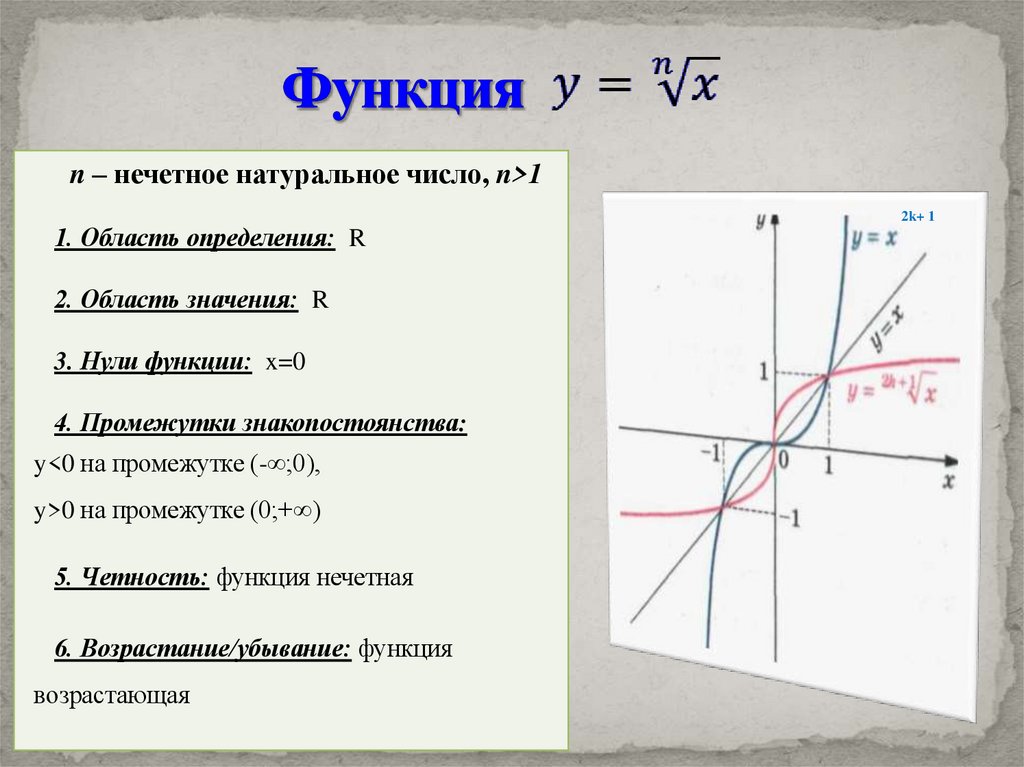
n – нечетное натуральное число, n>1
1. Область определения: R
2. Область значения: R
3. Нули функции: x=0
4. Промежутки знакопостоянства:
y<0 на промежутке (-∞;0),
y>0 на промежутке (0;+∞)
5. Четность: функция нечетная
6. Возрастание/убывание: функция
возрастающая
2k+ 1

8.

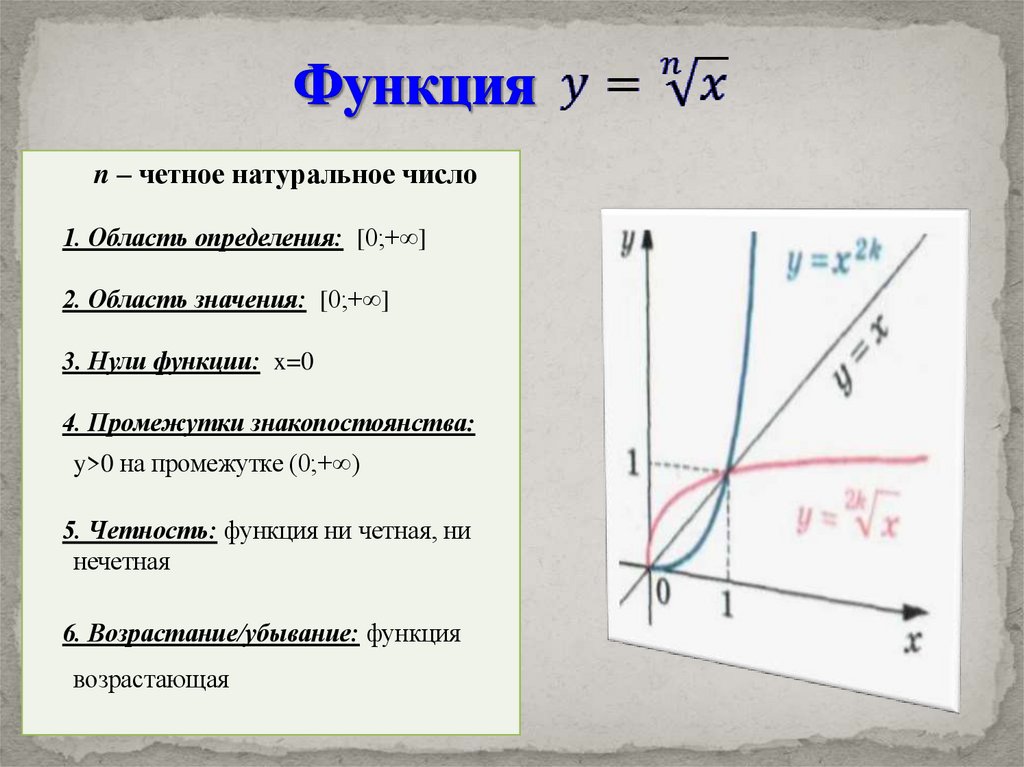
n – четное натуральное число
1. Область определения: [0;+∞]
2. Область значения: [0;+∞]
3. Нули функции: x=0
4. Промежутки знакопостоянства:
y>0 на промежутке (0;+∞)
5. Четность: функция ни четная, ни
нечетная
6. Возрастание/убывание: функция
возрастающая

9.

Определение: Степенью положительного числа а с
рациональным показателем r, поданным в виде , где m ϵ Z,
n ϵ N, n >1, называют число
, то есть
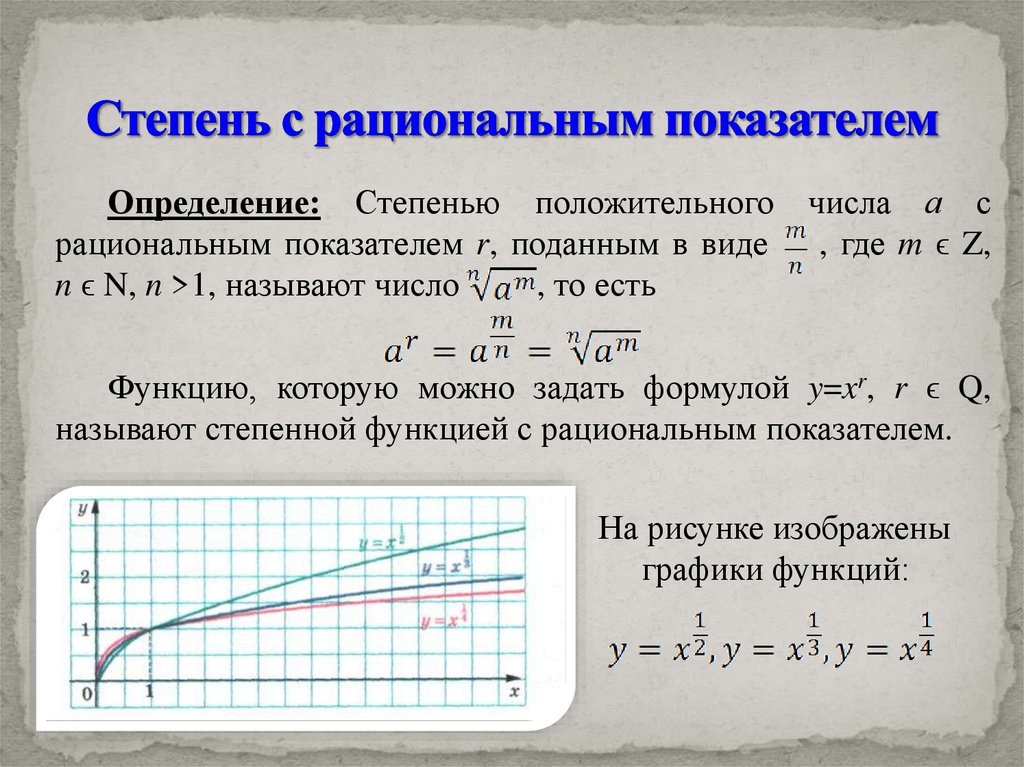
Функцию, которую можно задать формулой y=xr, r ϵ Q,
называют степенной функцией с рациональным показателем.
На рисунке изображены
графики функций:

10.

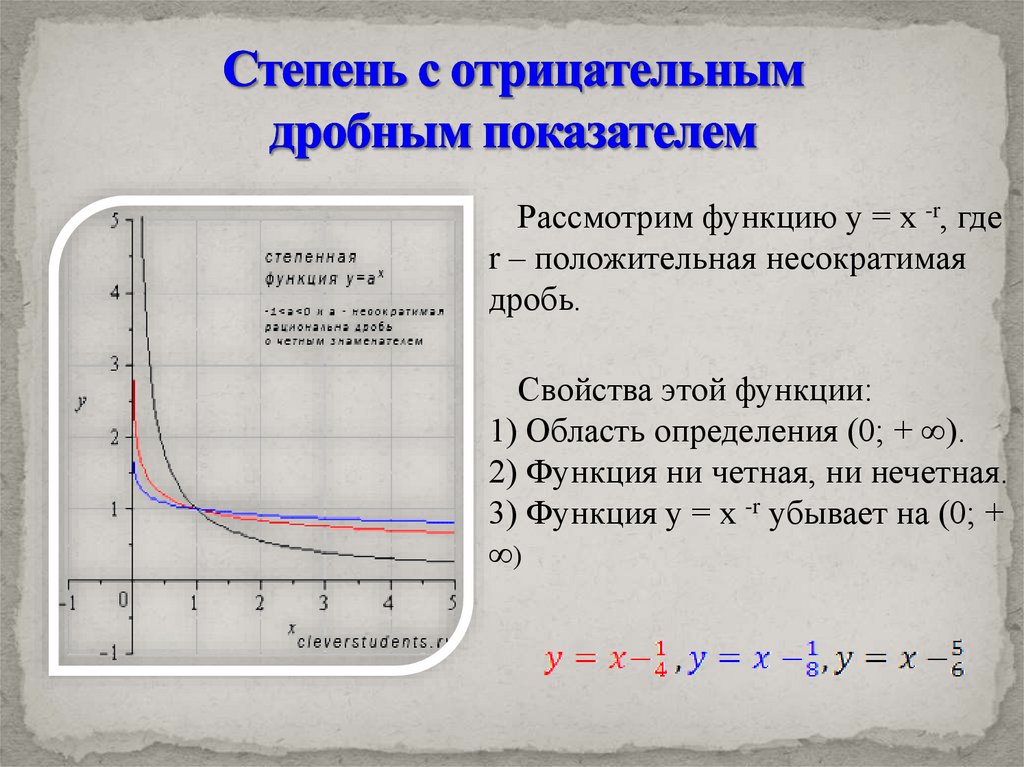
Рассмотрим функцию у = х -r, где
r – положительная несократимая
дробь.
Свойства этой функции:
1) Область определения (0; + ∞).
2) Функция ни четная, ни нечетная.
3) Функция у = х -r убывает на (0; +
∞)

11.

1.
Произведение
степеней.
Для
любого
а>0
и
любых
рациональных чисел p и q выполняется равенство:
Следствие. Для любого а>0 и любого рационального числа p
выполняется равенство
2. Частное степеней. Для любого а>0 и любых рациональных
чисел p и q выполняется равенство:

12.

3.
Степень степени. Для любого а>0 и любых рациональных
чисел p и q выполняется равенство:
4.
Степень произведения и степень дроби. Для любого а>0
и b >0 и любого рационального числа p выполняются
равенства

13.

Определение: Корнем n –ой степени из числа а, где n ϵ N,
n >1, называют такое число, n –ая степень которого равна а.
Примечание:
если n –четное натуральное число, то при а<0 корень n –ой
степени из числа а не существует; при а=0 корень n –ой степени
из числа а равен 0; при а>0 существуют два противоположные
числа, которые являются корнями n –ой степени из числа а.
если n –нечетное натуральное число, больше 1, то корень n –ой
степени из любого числа существует, при чем только один.

14.

Определение: Арифметическим корнем n –ой степени из
неотрицательного числа а, где n ϵ N, n >1, называют такое
неотрицательное число, n –ая степень которого равна а.
Примечание:
Для любого неотрицательного числа
а имеет место следующее:
выполняется равенство
n
a 0 и

15.

1. Корень из степени. Для любого а ϵ R и k ϵ N выполняются
равенства:
2. Корень из произведения. Если а≥0 и b≥0, n ϵ N, n>1, то
n
a b a b
n
n

16.

3. Корень из дроби. Если а≥0 и b>0, n ϵ N, n>1, то
n
a
a
n
n
b
b
4. Степень корня. Если а≥0, n ϵ N, k ϵ N n>1, то
n
a
k
a
k
n
5. Корень из корня. Если а≥0, n ϵ N, k ϵ N n>1, k>1 то
n k
a
nk
a
6. Если а≥0, n ϵ N, k ϵ N n>1, то
n k
a n a
k

17.

1. Найдем значение выражения
2. Найдем значение выражения
3. Найдем значение выражения

18.

1. Упростим выражение:
3
3
6
6 2 3 6 6 6
2. Упростим выражение: 3
3
3.
2 3 2 2 6 2
Упростим выражение:
4 3
2
4 3
3 4 3 3 12 3
3

19.

1. Упростим выражение:
4
81
625
3
10
2
27
4
81
81 3
4
4
625
625 5
2. Упростим выражение:
3
10
64
64 4
1
3 2
3
3
1
27
27
3
27 3

20.

1. Упростим выражение: 3 2
3
2
2 3
22 2 3
2
3
2
6 2
2. Упростим выражение: 6 7 4
6
4
7
3 2
4
7
3
2
7
3 49
3
2