Similar presentations:
Функции, их свойства и графики
1.
Функции,их свойства и графики
Коломина Н.Н.
2.
Немного историиСлово "функция" (от латинского functio —
совершение, выполнение) впервые употребил
в 1673 г. немецкий математик Лейбниц.
Коломина Н.Н.
В главном математическом труде
"Геометрия" (1637) Рене Декарта
впервые введено понятие переменной
величины, создан метод координат, введены
значки для переменных величин (x, y, z, ...)
Определения функции «Функция
переменного количества есть
аналитическое выражение,
cоставленное каким-либо образом из
этого количества и чисел или
постоянных количеств» сделал в 1748 г.
немецкий и российский математик
Леонард Эйлер
3.
Определение.«Зависимость переменной y от
переменной x, при которой каждому
значению переменной х
соответствует единственное
значение переменной у, называют
функцией».
у
6
5
4
3
2
1
х
-6
-5
-4
-3
-2
-1
0 1
-1
2
3
-2
Символически функциональная
зависимость между переменной у
(функцией) и переменной х
(аргументом) записывается с помощью
равенства y f ( x )
-3
-4
-5
-6
Способы задания функций: табличный (таблица),
графический(график), аналитический (формула).
Коломина Н.Н.
4
5
6
4.
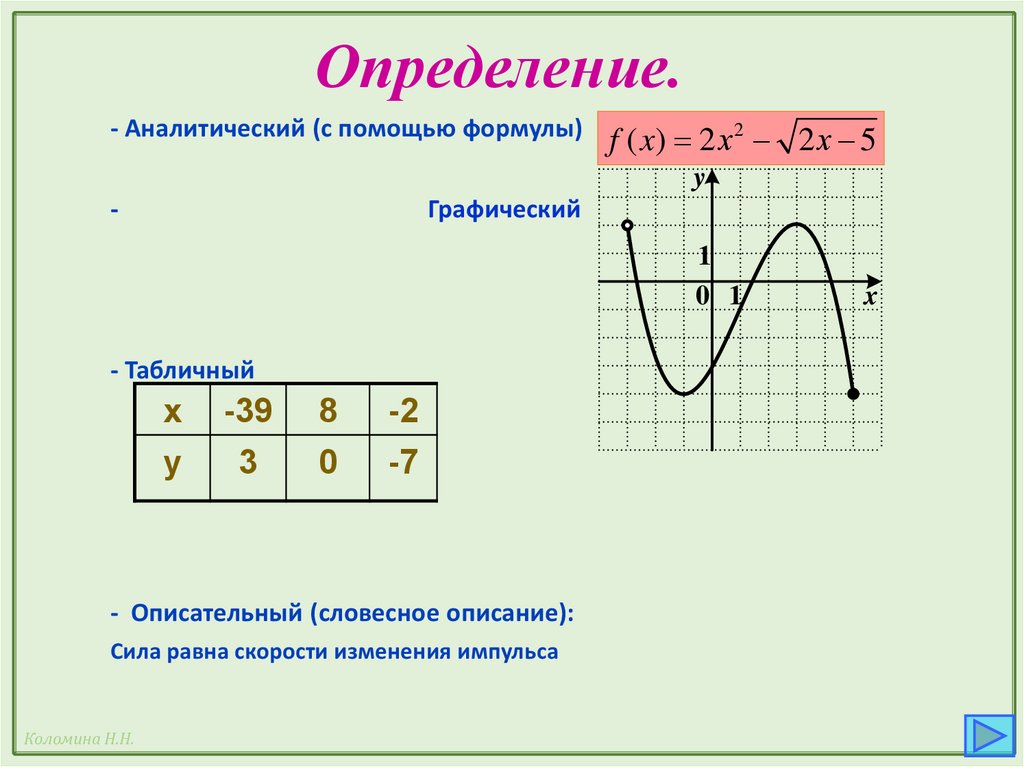
Определение.- Аналитический (с помощью формулы)
f ( x) 2 х 2 2 х 5
y
-
Графический
1
0 1
- Табличный
х
у
-39
3
8
0
-2
-7
- Описательный (словесное описание):
Сила равна скорости изменения импульса
Коломина Н.Н.
x
5.
Общая схема исследования функции1. Область определения функции.
2.Исследование области значений функции.
3. Исследование функции на четность.
4.Исследование промежутков возрастания и убывания
функции.
5. Исследование функции на монотонность.
5. Исследование функции на экстремум.
6. Исследование функции на периодичность.
7. Определение промежутков знакопостоянства.
8.Определение точек пересечения графика функции с осями
координат.
9. Построение графика функции.
Коломина Н.Н.
6.
Область определения функцииОбласть определения функции – все значения,
которые принимает независимая переменная.
Обозначается : D (f).
Пример. Функция задана формулой у =
6
х 2 9
Данная формула имеет смысл при всех значениях
х ≠ -3, х ≠ 3,
поэтому D( y )=(- ∞;-3) U (-3;3) U (3; +∞)
Коломина Н.Н.
7.
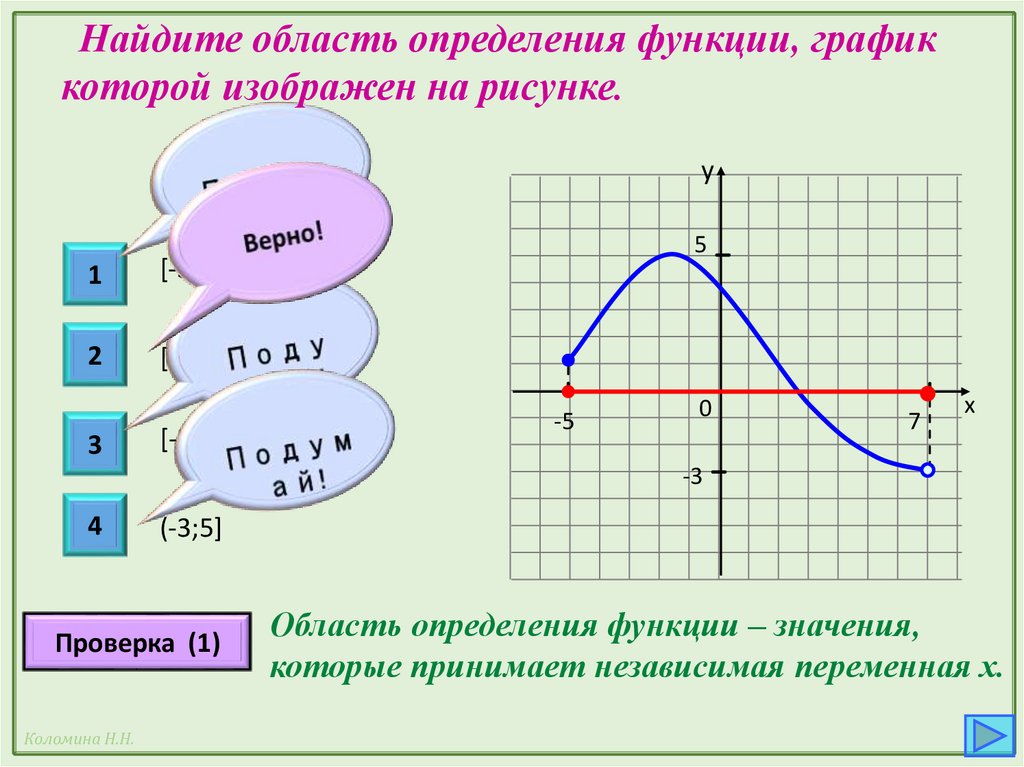
Найдите область определения функции, графиккоторой изображен на рисунке.
у
1
[-3;5]
2
[-5;7)
3
[-5;7]
5
-5
0
7
х
-3
4
(-3;5]
Проверка (1)
Коломина Н.Н.
Область определения функции – значения,
которые принимает независимая переменная х.
8.
Область значений функцииОбласть (множество) значений функции – все
значения, которые принимает зависимая
переменная.
Обозначается : E (f)
Пример. Функция задана формулой у =
х 9
2
Данная функция является квадратичной , график – парабола,
вершина (0; 9)
поэтому E( y )= [ 9 ; +∞)
Коломина Н.Н.
9.
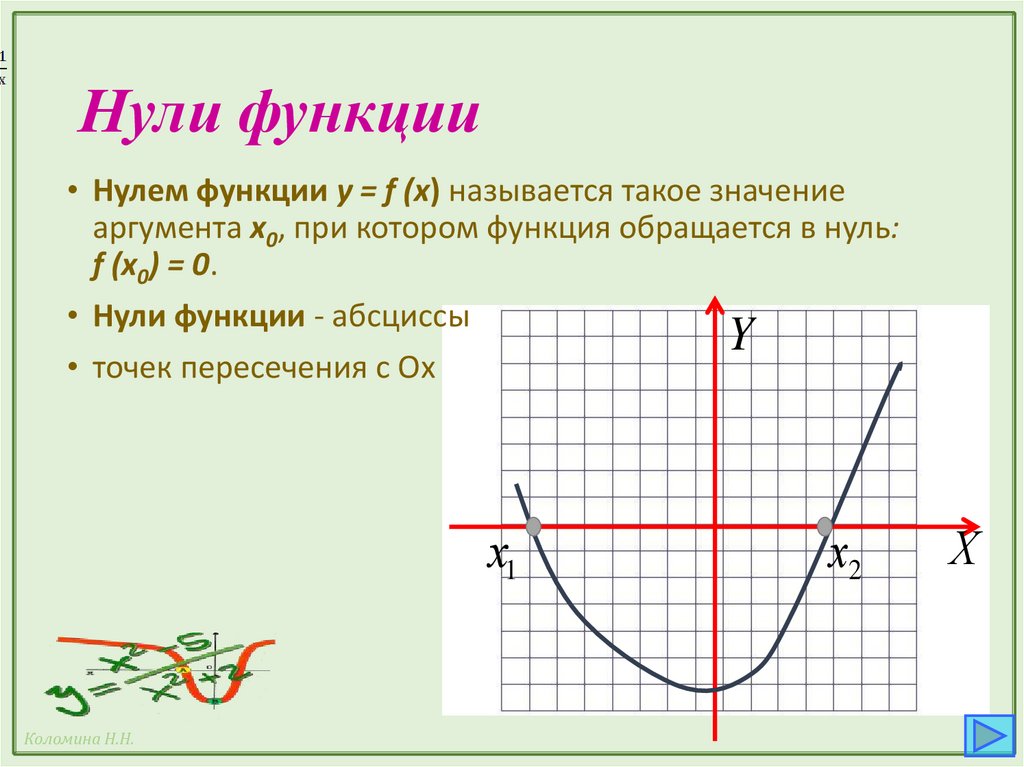
Нули функции• Нулем функции y = f (x) называется такое значение
аргумента x0, при котором функция обращается в нуль:
f (x0) = 0.
• Нули функции - абсциссы
Y
• точек пересечения с Ох
х1
Коломина Н.Н.
х2
Х
10.
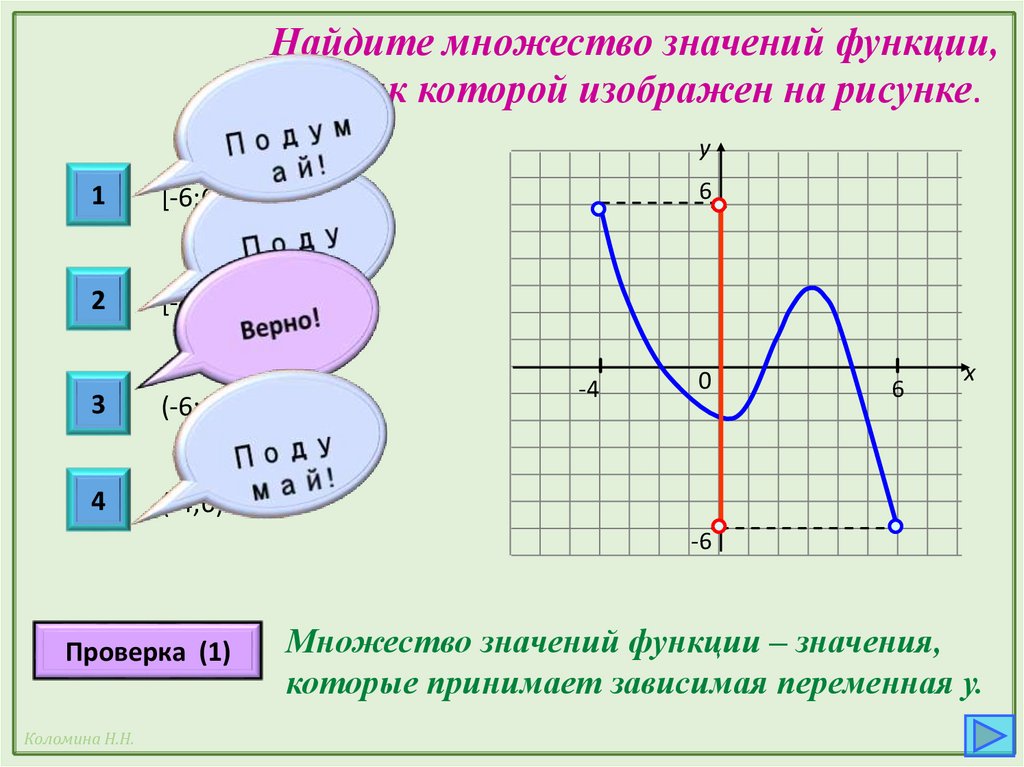
Найдите множество значений функции,график которой изображен на рисунке.
у
1
[-6;6]
2
[-4;6]
3
(-6;6)
4
(-4;6)
6
-4
0
6
х
-6
Проверка (1)
Коломина Н.Н.
Множество значений функции – значения,
которые принимает зависимая переменная у.
11.
Исследование функции на четность.Функция y f ( х ) называется четной , если при всех
значений х в области определения этой функции
при изменения знака аргумента на
противоположный значение функции не изменяется,
т.е. f ( х ) f ( х ) .
Например, парабола у= Х2 является четной
функцией, т.к. (-Х2)= Х2 .
График четной функции симметричен относительно оси
Коломина Н.Н.
оу.
12.
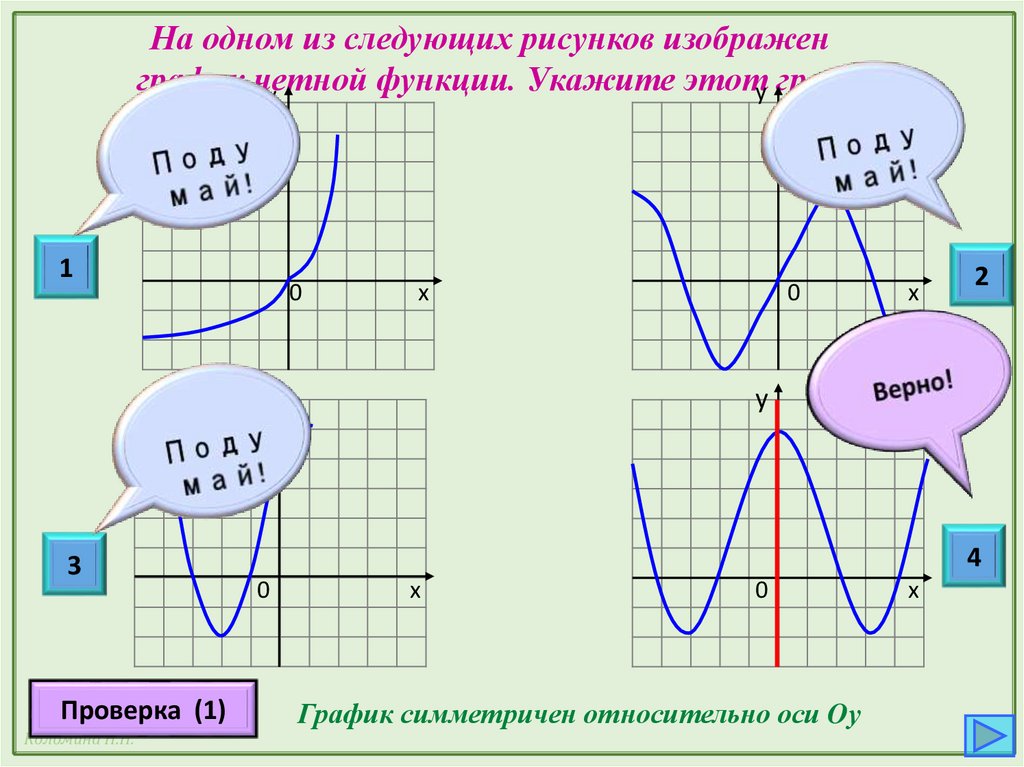
На одном из следующих рисунков изображенграфик четной
функции. Укажите этоту график.
у
1
0
х
у
3
Проверка (1)
Коломина Н.Н.
0
х
2
у
4
0
х
0
График симметричен относительно оси Oу
х
13.
Функция y f ( х ) называется нечетной, если привсех значениях х в области определения этой
функции при изменении знака аргумента на
противоположный функция изменяется только по
знаку, т.е. f ( х ) f (х ) .
Например, функция у= Х3 – нечетная, т.к. (-Х)3 = -Х3.
График нечетной функции симметричен
относительно начала координат.
Свойством четности или нечетности обладает не
всякая функция. Например, функция f ( х ) Х2+ Х3
не является ни четной, ни нечетной:
f ( х ) (-Х)2+ (-Х)3 = Х2 – Х3;
Коломина Н.Н.
2 – Х3;
Х
Х2 + Х3=
/
14.
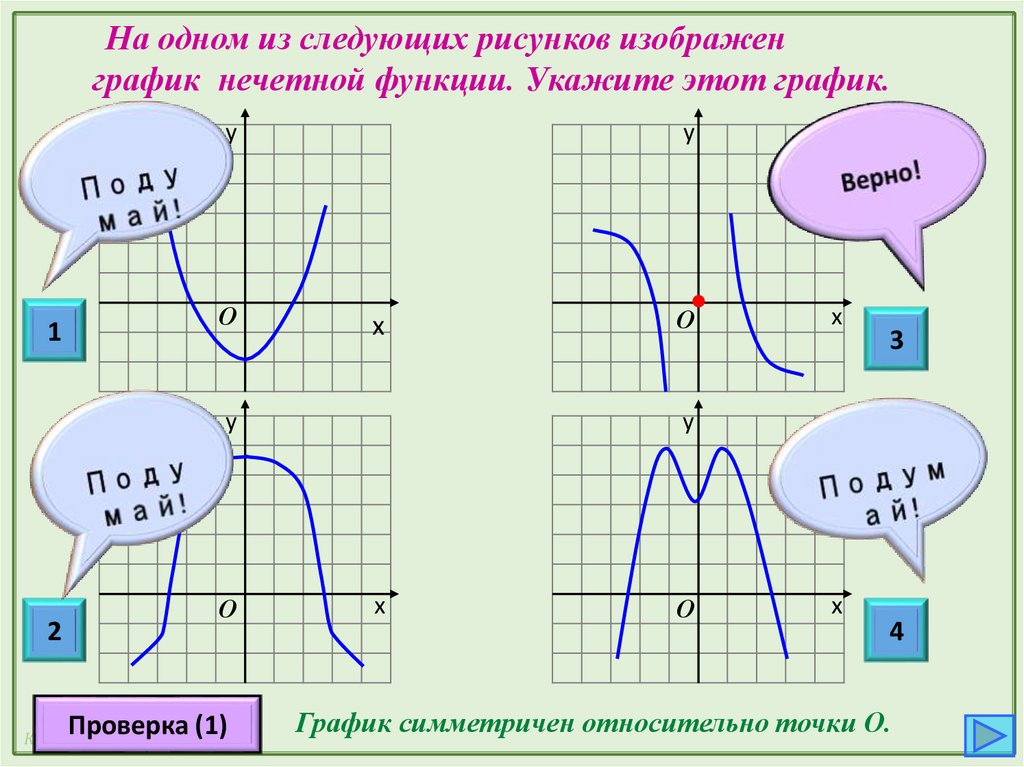
На одном из следующих рисунков изображенграфик нечетной функции. Укажите этот график.
у
О
1
у
х
у
О
2
Проверка (1)
Коломина Н.Н.
О
х
3
у
х
О
х
4
График симметричен относительно точки О.
15.
Определение промежутков возрастанияи убывания
f ( х1)
/\
/\
Среди множества функций есть функции, значения которых с
увеличением аргумента только возрастают или только
убывают. Такие функции называются возрастающими или
убывающими.
Функция y f ( х ) называется возрастающей в
промежутке а х в, если для любых Х1 и Х2 , принадлежащих
этому промежутку, при Х1 Х2 имеет место неравенство
f ( х2)
/\
Функция y f ( х ) называется убывающей в
промежутке а х в, если для любых Х1 и Х2, принадлежащих
этому промежутку, при Х1 Х2 имеет место неравенство
f ( х1) > f ( х2)
Коломина Н.Н.
16.
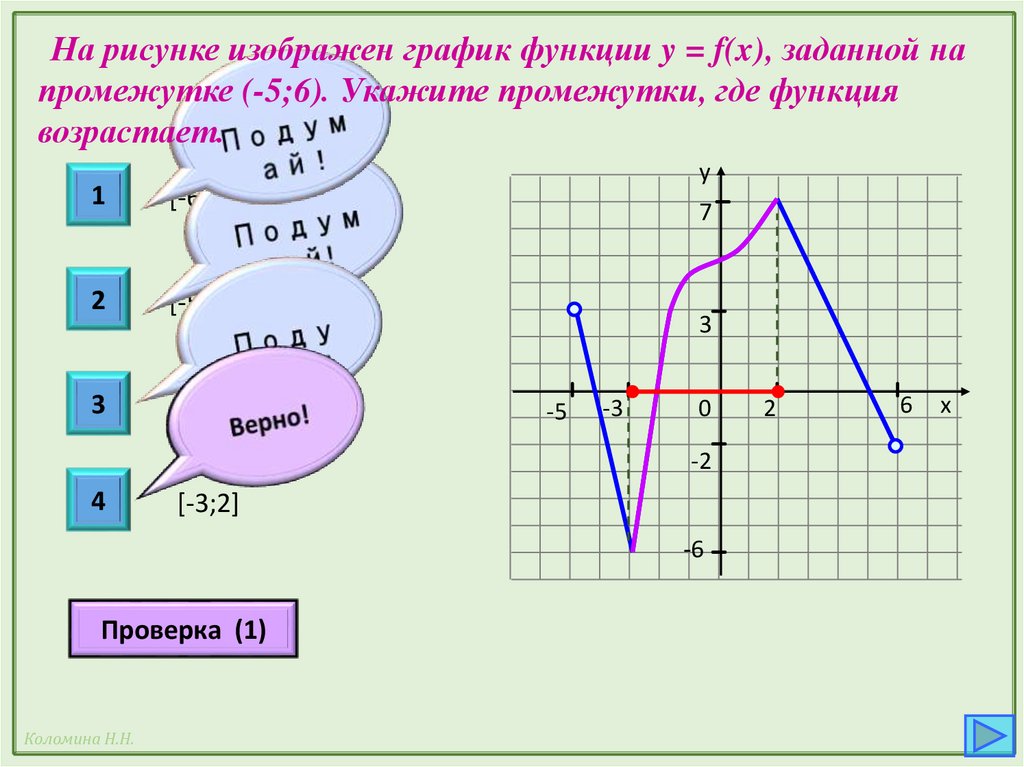
На рисунке изображен график функции y = f(x), заданной напромежутке (-5;6). Укажите промежутки, где функция
возрастает.
1
[-6;7]
2
[-5;-3] U [2;6]
3
[-3;7]
у
7
3
-5
-3
0
-2
4
[-3;2]
-6
Проверка (1)
Коломина Н.Н.
2
6
х
17.
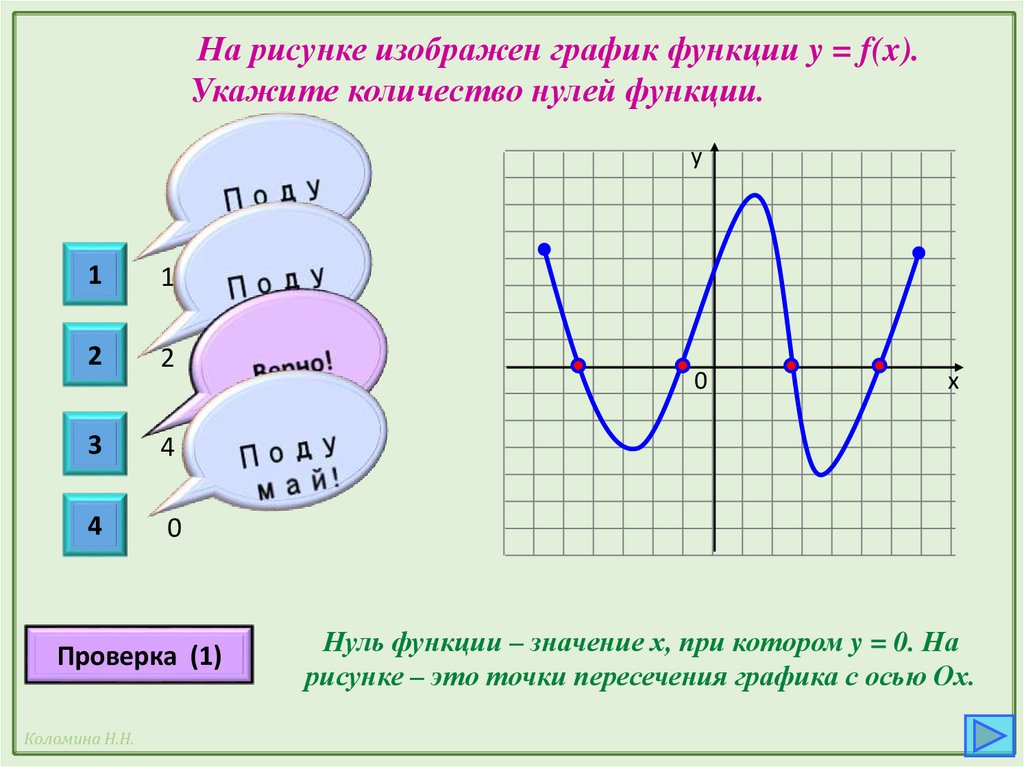
На рисунке изображен график функции y = f(x).Укажите количество нулей функции.
y
1
1
2
2
3
4
4
0
Проверка (1)
Коломина Н.Н.
0
х
Нуль функции – значение х, при котором y = 0. На
рисунке – это точки пересечения графика с осью Ох.
18.
Какие из функций являютсявозрастающими, а какие убывающими?
1) y 5
возрастающая, т.к.5 1
x
2) y 0,5
3) y 10
x
убывающая, т.к.0 0,5 1
x
возрастающая, т.к.10 1
ая, т.к. 1
4) y x возрастающ
x
2
2
5) y убывающая, т.к.0 1
3
3
6) y 49
Коломина Н.Н.
x
1
1
убывающая, т.к.49 и 0
1
49
49
1
19.
Исследование функции на монотонность.Как возрастающие, так и убывающие функции
называются монотонными, а промежутки, в
которых функция возрастает или убывает, промежутками монотонности.
Например, функция у= Х2 при х 0 монотонно
возрастает.
Функция у= Х3 на всей числовой оси монотонно
возрастает, а
функция у= -Х3 на всей числовой оси монотонно
убывает.
Коломина Н.Н.
20.
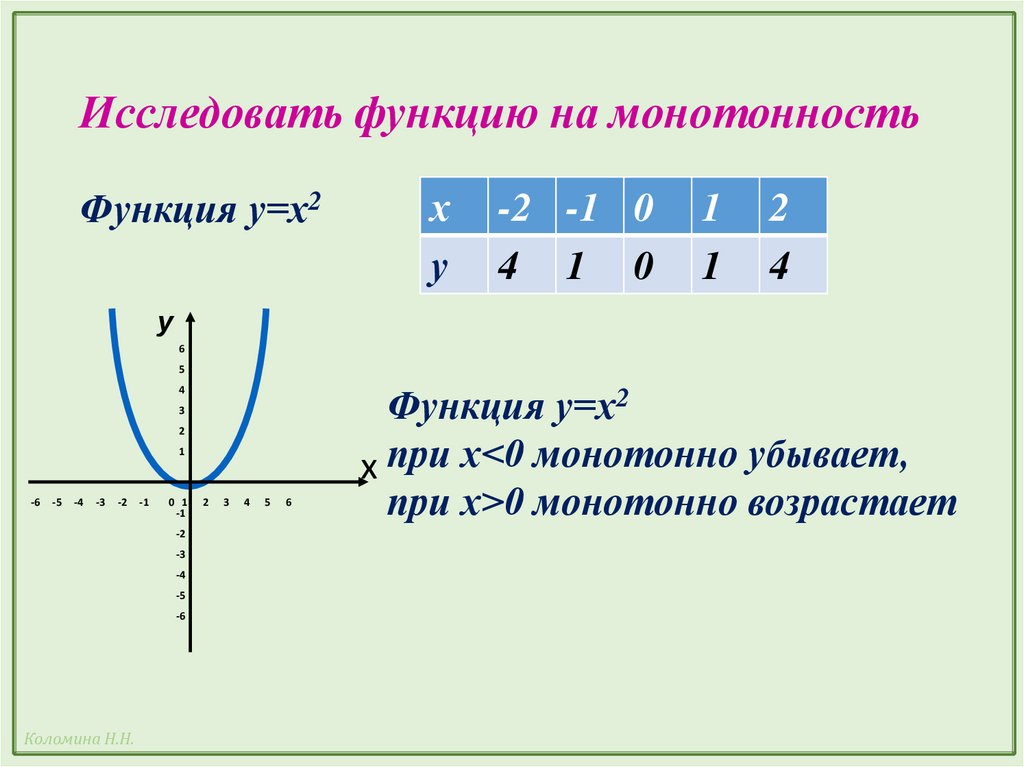
Исследовать функцию на монотонностьФункция у=х2
х
у
-2 -1 0
4 1 0
1
1
2
4
y
6
5
4
3
2
1
-6
-5
-4
-3
-2
-1
0 1
-1
-2
-3
-4
-5
-6
Коломина Н.Н.
2
3
4
5
6
Функция у=х2
х при х<0 монотонно убывает,
при х>0 монотонно возрастает
21.
Обратная функцияЕсли функция y f ( х ) принимает каждое свое
значение только при единственном значении х, то
такую функцию называют обратимой.
Например, функция у=3х+5 является обратимой, т.к.
каждое значение у принимается при единственном
значении аргумента х. Напротив, функция у= 3Х2 не
является обратимой, поскольку, например, значение
у=3 она принимает и при х=1, и при х=-1.
Для всякой непрерывной функции (такой, которая не
имеет точек разрыва) существует монотонная
однозначная и непрерывная обратная функция.
Коломина Н.Н.
22.
Линейная функция y=kx+bСвойства линейной функции y = kx + b:
1.D(f) = (– ; + ).
2.E(f) = (– ; + ).
3.Если b = 0, то функция нечетная.
4.а) Нули функции: (– b/k; 0);
б) точка пересечения с Оу: (0; b).
5.а) возрастает, если k > 0;
б) убывает, если k < 0.
6.Не ограничена ни снизу, ни сверху.
7.Нет ни наибольшего, ни наименьшего значений.
8.Функция непрерывна на множестве (– ; + ).
Коломина Н.Н.
23.
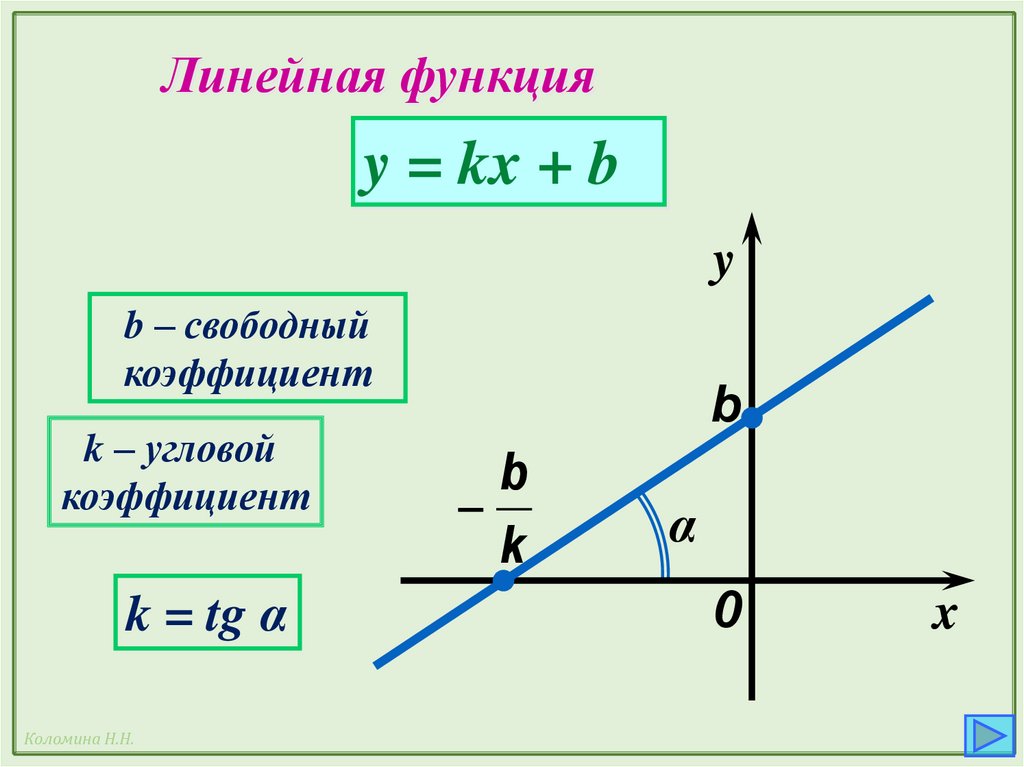
Линейная функцияy = kx + b
y
b – свободный
коэффициент
k – угловой
коэффициент
k = tg α
Коломина Н.Н.
b
b
k
α
0
x
24.
Линейная функция y=kx+by
0
b
Коломина Н.Н.
b
k
x
25.
kОбратная пропорциональность у = x
Свойства функции y = k/x:
1.D(f) = (– ; 0) (0; + ).
2.E(f) = (– ; 0) (0; + ).
3.Функция нечетная.
4.а) Нули функции: нет;
б) точка пересечения с Оу: нет.
5.а) если k < 0, то (– ; 0) и (0; + ) – промежутки
возрастания функции;
б) если k > 0, то (– ; 0) и (0; + ) – промежутки
убывания функции.
6.Не ограничена ни снизу, ни сверху.
7.Нет ни наибольшего, ни наименьшего значений.
8.Функция непрерывна на каждом из промежутков
(– ; 0) и (0; + ).
Коломина Н.Н.
26.
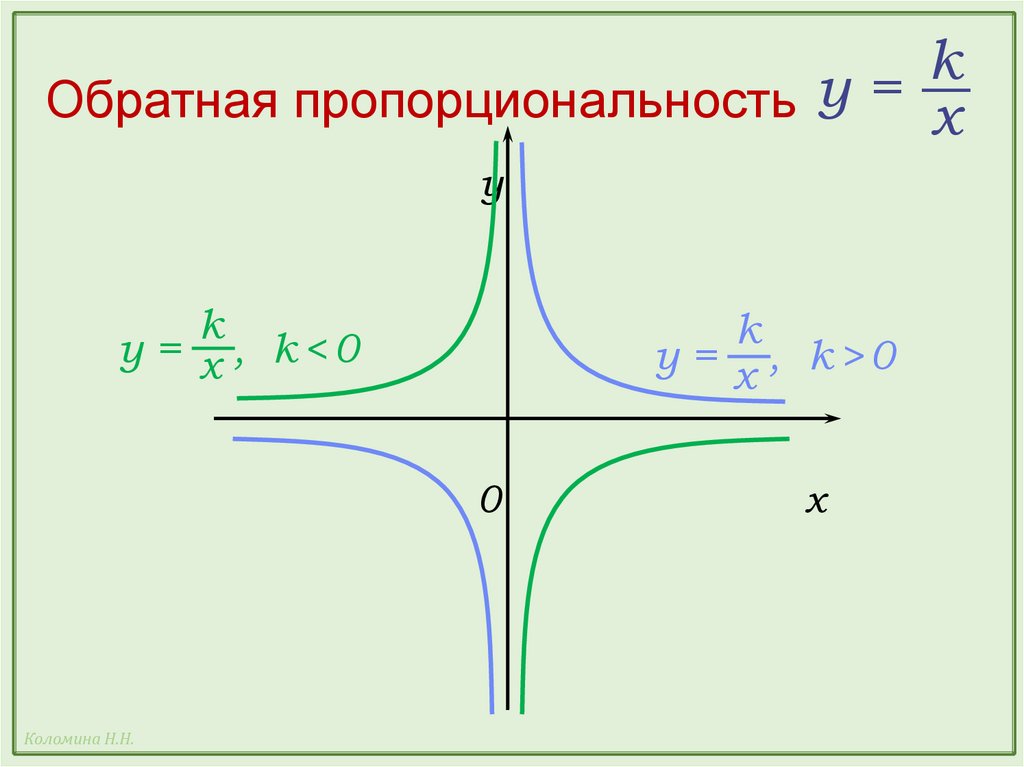
kОбратная пропорциональность у = x
y
k
у = x , k<0
k
у = x , k>0
0
Коломина Н.Н.
x
27.
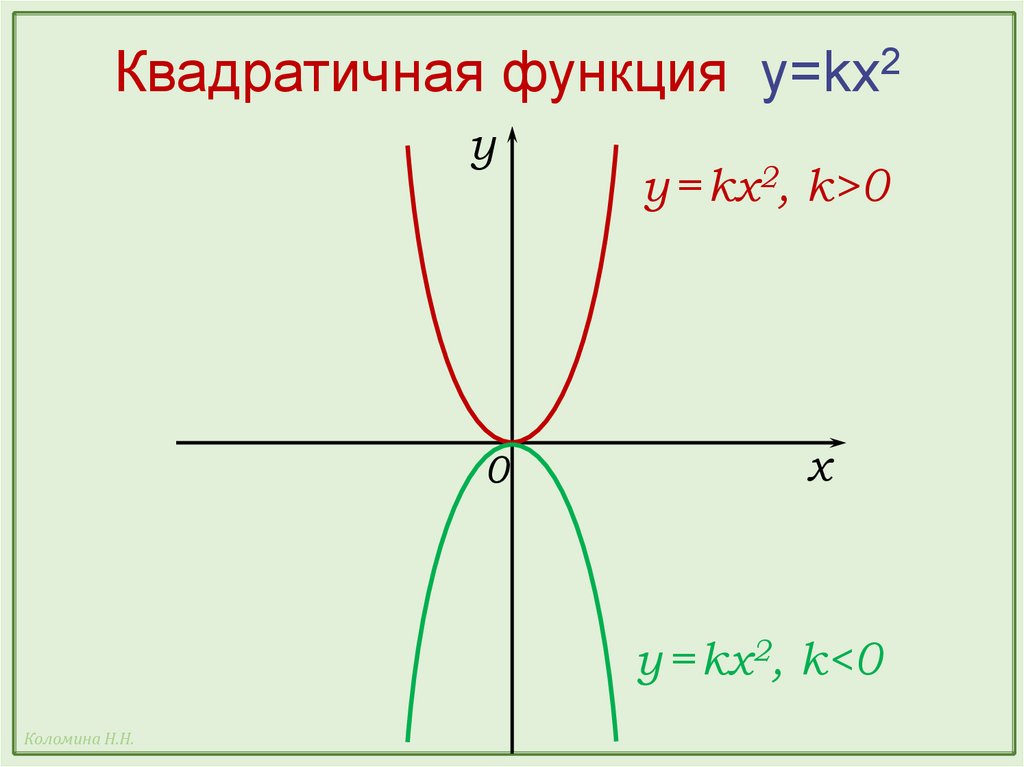
Квадратичная функция y=kx2Свойства функции y = kx2 при k > 0:
1.D(f) = (– ; + ).
2.E(f) = [0; + ).
3.Функция четная.
4.а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
5.а) [0; + ) – промежуток возрастания функции;
б) (– ; 0] – промежуток убывания функции.
6.Ограничена снизу, не ограничена сверху.
7.а) унаим. = 0;
б) унаиб. – не существует.
8.Непрерывна на множестве (– ; + ).
9.Выпукла вниз.
Коломина Н.Н.
28.
Квадратичная функция y=kx2Свойства функции y = kx2 при k < 0:
1.D(f) = (– ; + ).
2.E(f) = (– ; 0].
3.Функция четная.
4.а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
5.а) [0; + ) – промежуток убывания функции;
б) (– ; 0] – промежуток возрастания функции.
6.Ограничена сверху, не ограничена снизу.
7.а) унаиб. = 0;
б) унаим. – не существует.
8.Непрерывна на множестве (– ; + ).
9.Выпукла вверх.
Коломина Н.Н.
29.
Квадратичная функция y=kx2y
0
y = kx2, k>0
x
y = kx2, k<0
Коломина Н.Н.
30.
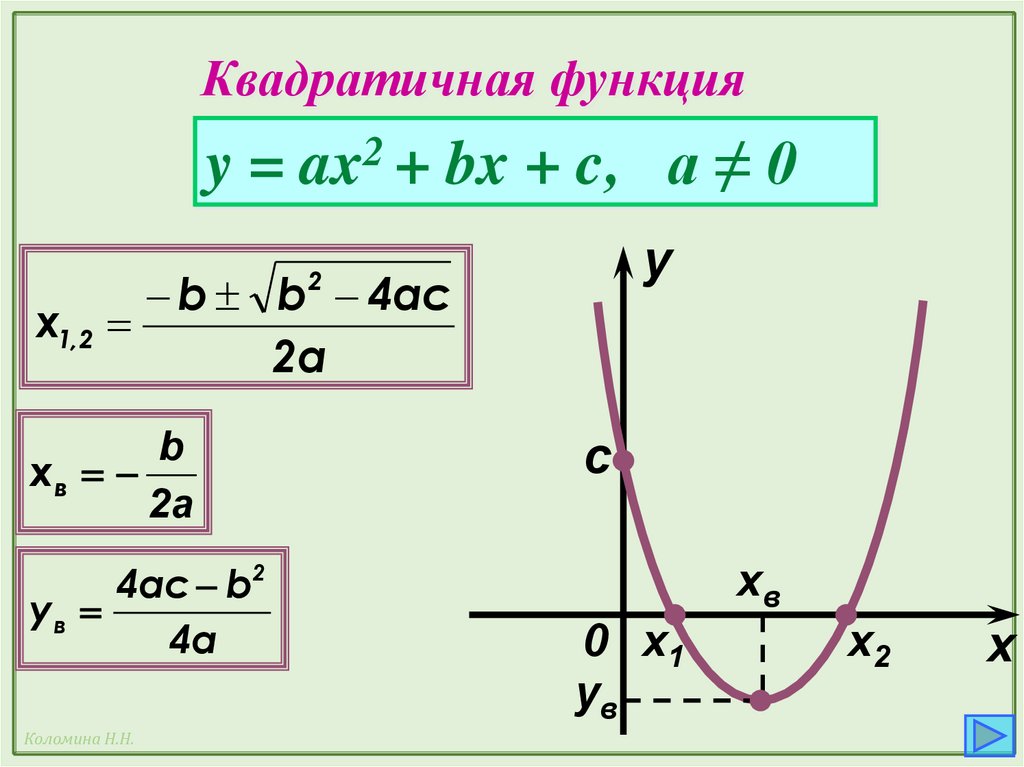
Квадратичная функцияy = ax2 + bx + c, а ≠ 0
y
2
b b 4ac
x1,2
2a
b
xв
2а
4ac b
yв
4a
Коломина Н.Н.
c
2
xв
0 x1
ув
x2
x
31.
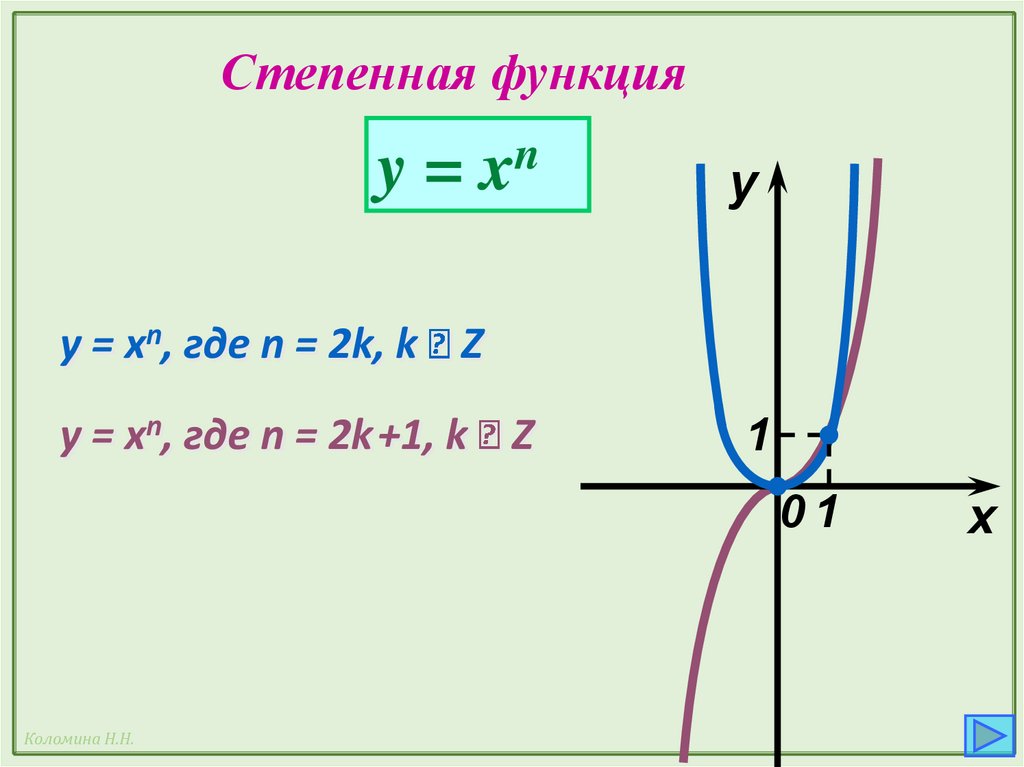
Степенная функцияn
y=x
y
y = xn, где n = 2k, k Z
y = xn, где n = 2k+1, k Z
1
01
Коломина Н.Н.
x
32.
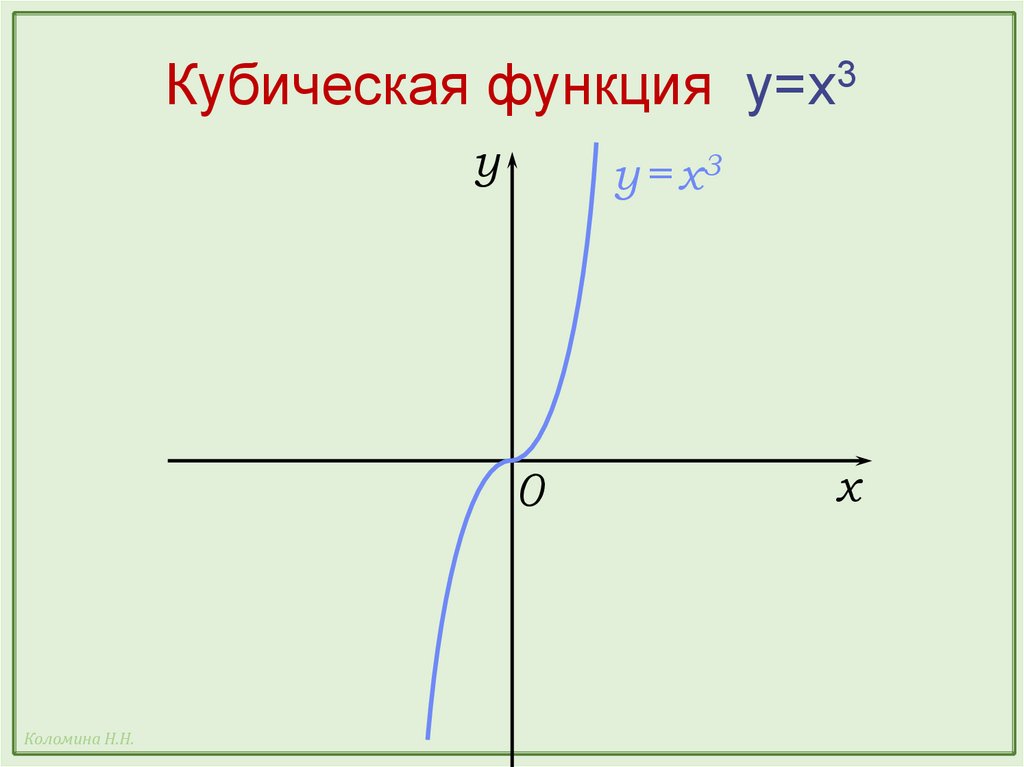
Кубическая функция y=x3Свойства кубической функции y = x3:
1.D(f) = (– ; + ).
2.E(f) = (– ; + ).
3.Функция нечетная.
4.а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
5.Возрастает на множестве (– ; + ).
6.Не ограничена ни снизу, ни сверху.
7.Нет ни наибольшего, ни наименьшего значений.
8.Функция непрерывна на множестве (– ; + ).
Коломина Н.Н.
33.
Кубическая функция y=x3y
y = x3
0
Коломина Н.Н.
x
34.
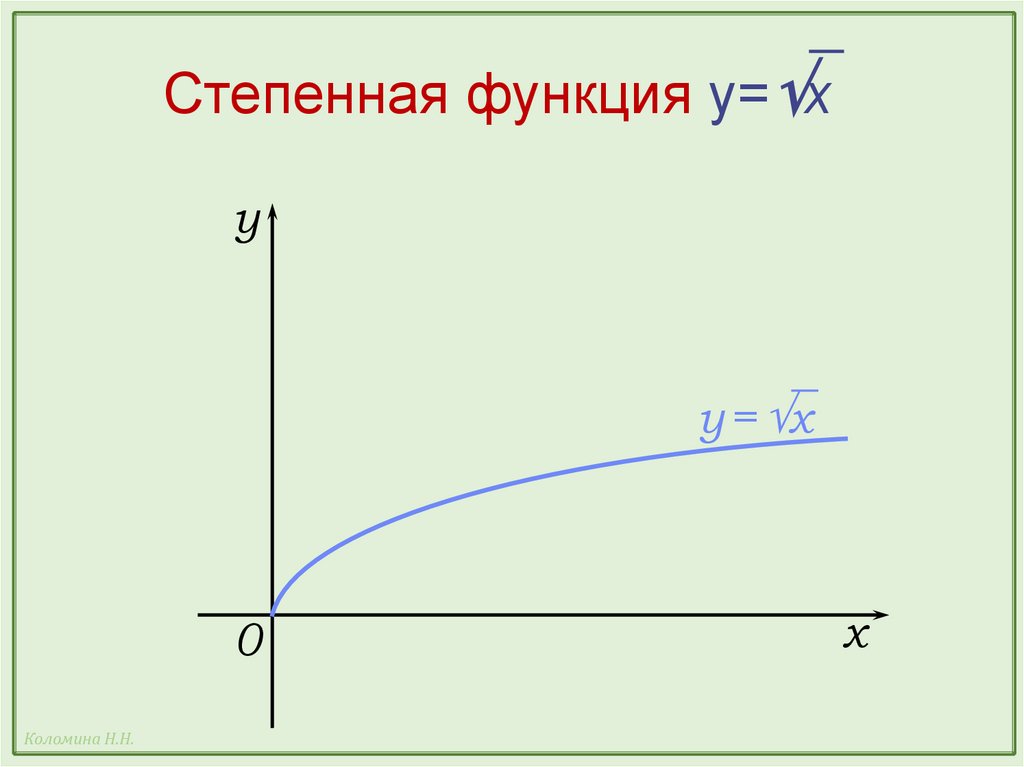
Степенная функция y= xСвойства функции y = x:
1.D(f) = [0; + ).
2.E(f) = [0; + ).
3.Функция ни четная, ни нечетная.
4.а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
5.[0; + ) – промежуток возрастания функции.
6.Ограничена снизу, не ограничена сверху.
7.а) унаим. = 0;
б) унаиб. – не существует.
8.Непрерывна на множестве [0; + ).
9.Выпукла вверх.
Коломина Н.Н.
35.
Степенная функция y= xy
y = x
0
Коломина Н.Н.
x
36.
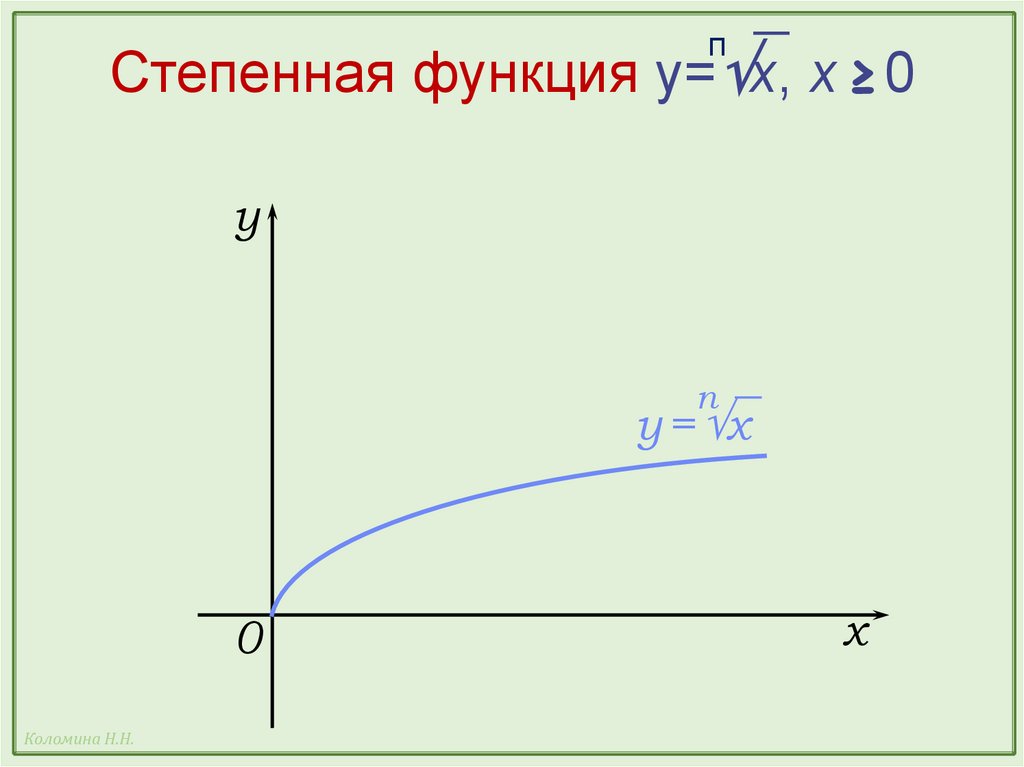
пСтепенная функция y= x, х ≥0
n
Свойства функции y = x, х ≥ 0:
1.D(f) = [0; + ).
2.E(f) = [0; + ).
3.Функция ни четная, ни нечетная.
4.а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
5.[0; + ) – промежуток возрастания функции.
6.Ограничена снизу, не ограничена сверху.
7.а) унаим. = 0;
б) унаиб. – не существует.
8.Непрерывна на множестве [0; + ).
9.Выпукла вверх.
Коломина Н.Н.
37.
пСтепенная функция y= x, х ≥0
y
п
y = x
0
Коломина Н.Н.
x
38.
пСтепенная функция y= x,
п - нечетное
n
Свойства функции y = x, n = 2k+1:
1.D(f) = (– ; + ).
2.E(f) = (– ; + ).
3.Функция нечетная.
4.а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
5.Возрастает на множестве (– ; + ).
6.Не ограничена ни снизу, ни сверху.
7.Нет ни наибольшего, ни наименьшего значений.
8.Функция непрерывна на множестве (– ; + ).
Коломина Н.Н.
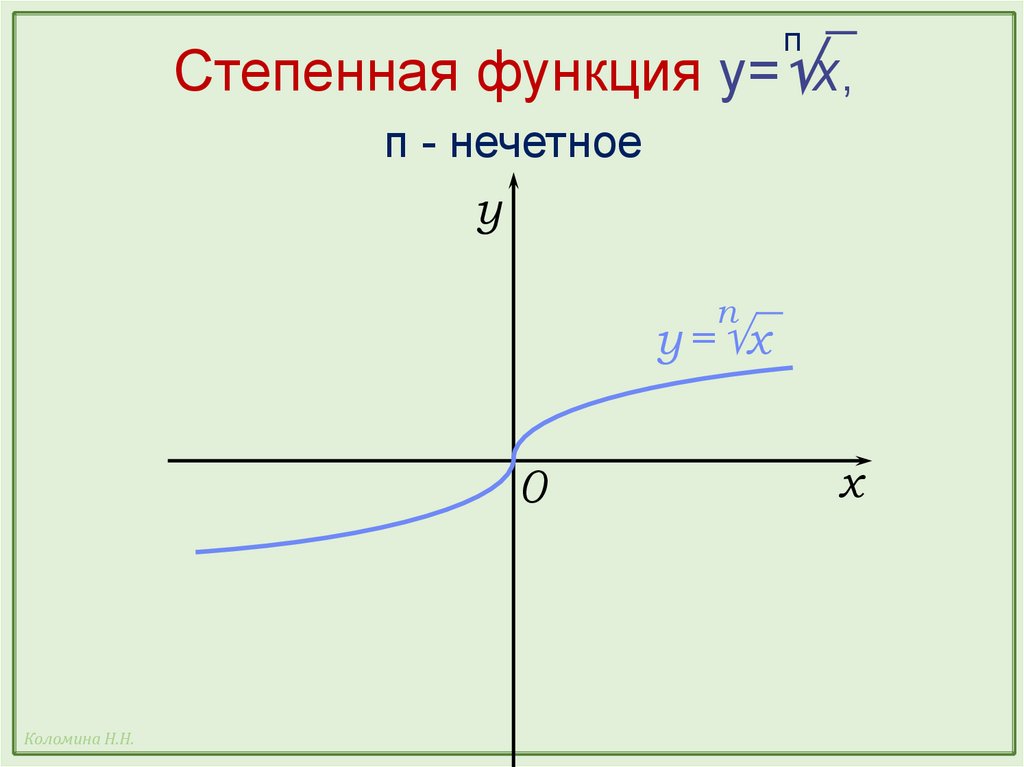
39.
пСтепенная функция y= x,
п - нечетное
y
п
y = x
0
Коломина Н.Н.
x
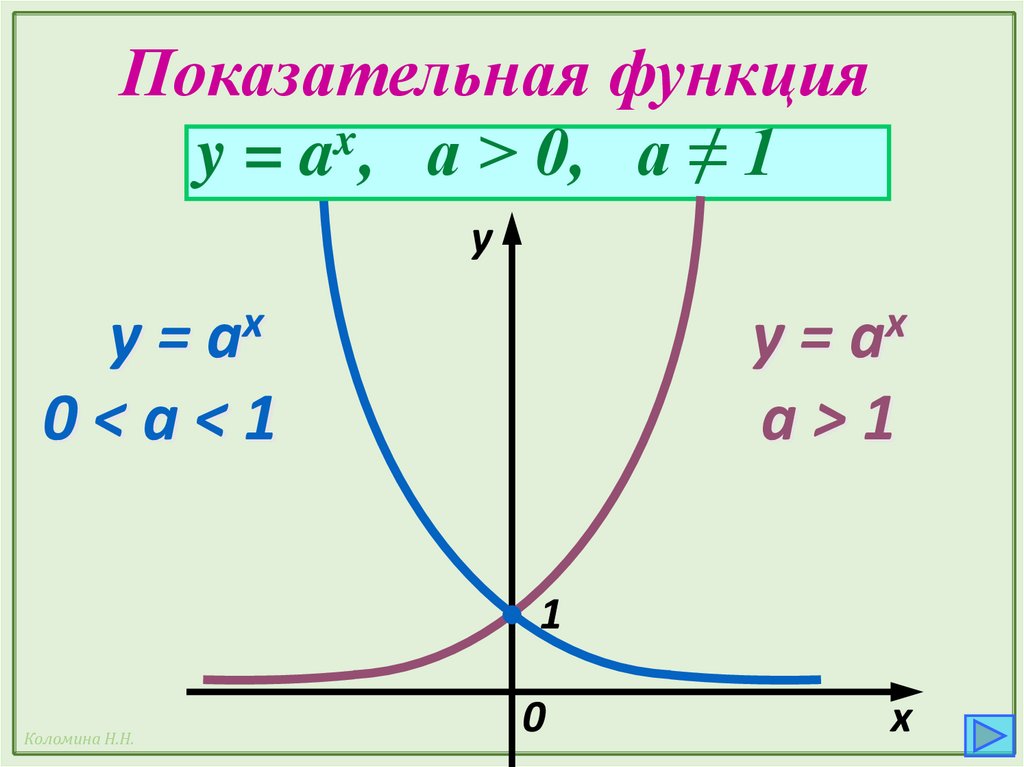
40.
Показательная функцияy = ax, а > 0, a ≠ 1
y
y = ax
0<a<1
y = ax
a>1
1
Коломина Н.Н.
0
x
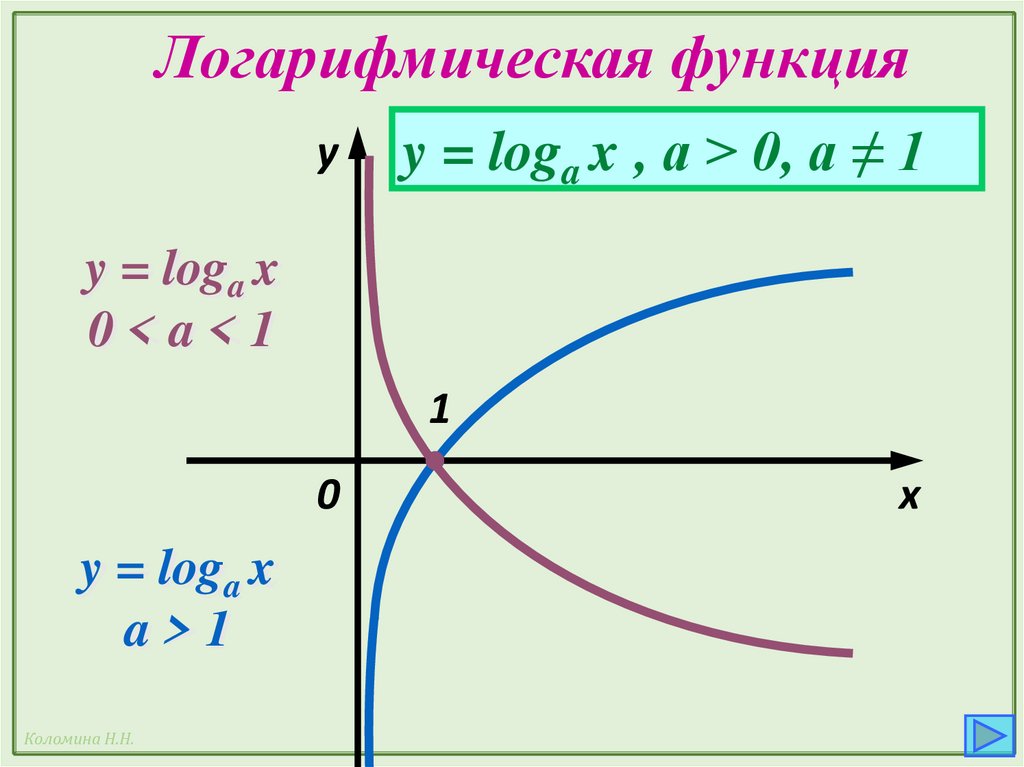
41.
Логарифмическая функцияy
y = loga x , а > 0, a ≠ 1
y = loga x
0<a<1
1
0
y = loga x
a>1
Коломина Н.Н.
x




















 mathematics
mathematics








