Similar presentations:
Функции. Их свойства и графики
1.
Функции их свойстваи графики
●Что такое «функция»?
●Способы задания функции.
●Схема исследования функции.
2.
Определение функции.Функцией называется зависимость между двумя
переменными (У и Х), в которой каждому значению
независимой переменной (Х) соответствует
единственное значение зависимой переменной (У).
Независимую переменную называют - аргумент.
Значения зависимой переменной называют
значениями функции.
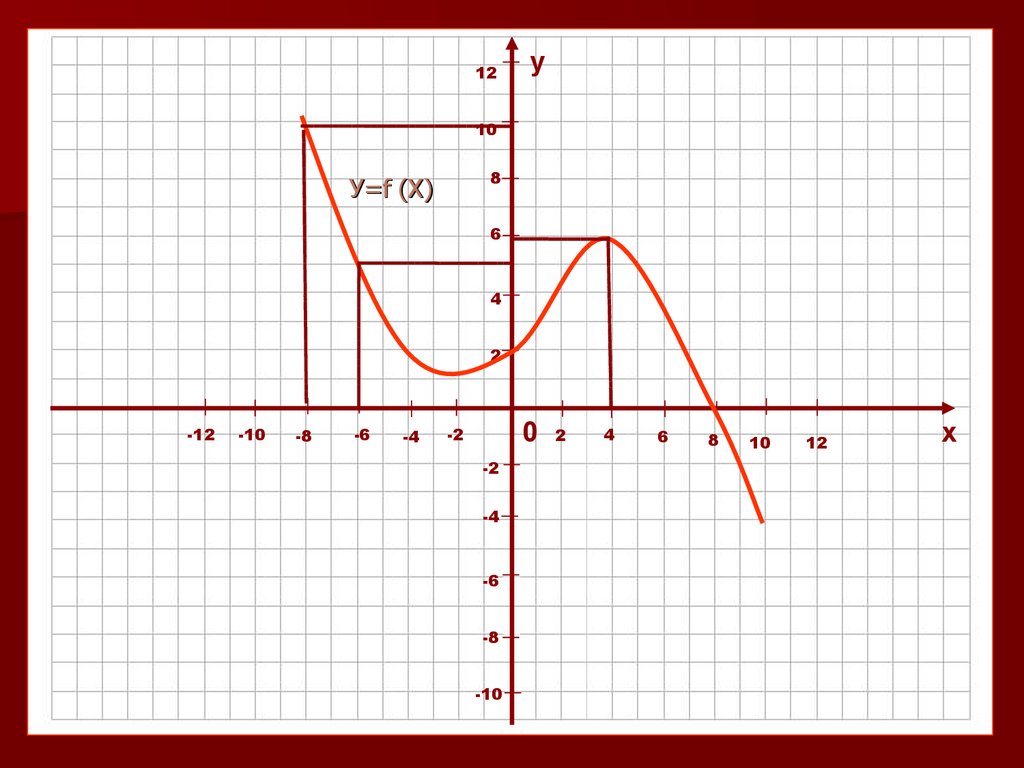
Запись У=f (X) читается: У – функция от Х.
3.
12у
10
8
У=f (X)
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
4.
Способы задания функции.Графически.
С помощью формулы.
Таблицей.
Словесный.
Рекуррентный.
5.
100S (в км)
80
60
40
20
t (в сек)
0
2
4
6
8
10
12
14
6.
У=х -3х+5У=-2х+1
У=|X|-5
2
7.
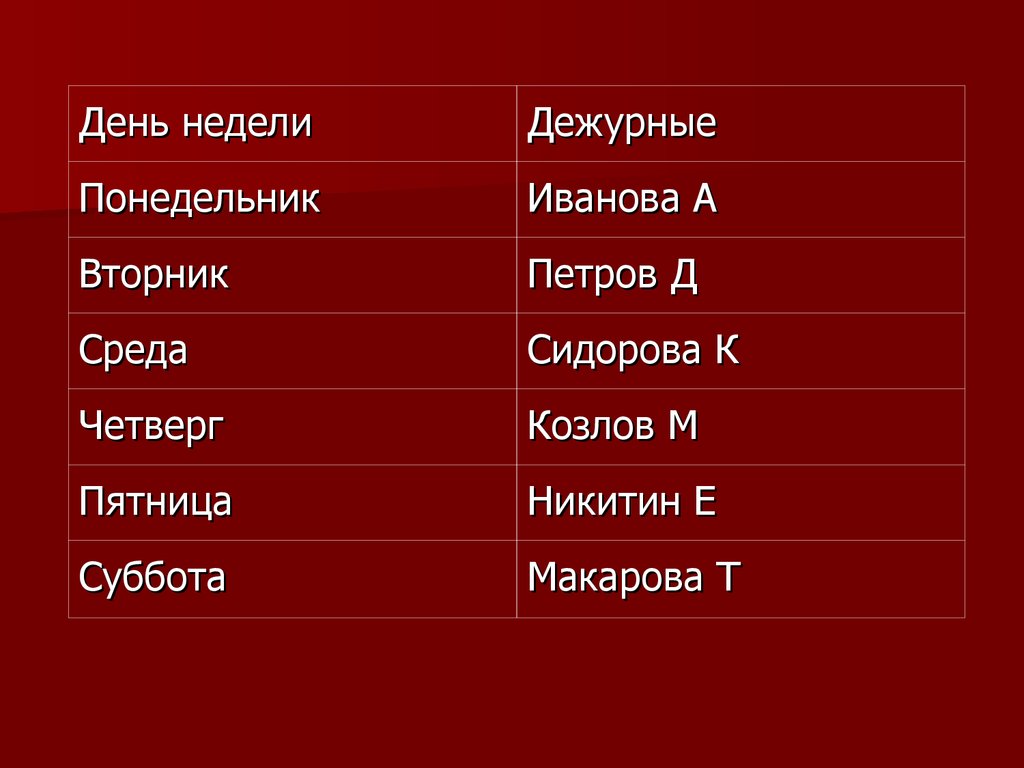
День неделиДежурные
Понедельник
Иванова А
Вторник
Петров Д
Среда
Сидорова К
Четверг
Козлов М
Пятница
Никитин Е
Суббота
Макарова Т
8.
Каждому натуральному числупоставим в соответствие его
квадрат.
9.
а1=3,аn+1= 2аn-1.
10.
1. Область определенияВсе значения независимой переменной
образуют область определения функции
-D (f). Значения независимой переменной
находятся на оси абсцисс (Ох)
11.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
2
4
6
-2
-4
-6
-8
-10
D (f).
8
10
12
х
12.
Если функция задана формулой и не указана ее областьопределения, то область определения функции состоит из всех
значений аргумента, при которых формула имеет смысл.
Укажите область определения функций:
а)
, б)
, в)
13.
2. Область значений функции.Все значения, которые принимает
зависимая переменная, образуют область
значений функции – E (f).
Значения зависимой переменной находятся
на оси ординат (Оу)
Единственная область, которая записывается
по оси Оу
14.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
2
4
6
8
10
х
12
-2
-4
-6
-8
-10
E (f).
15.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
2
4
6
8
10
х
12
-2
E (f).
-4
-6
-8
-10
D (f).
16.
3. Промежутки знакопостоянствау=5х^2-3х-2 график парабола, ветви вверх
Решите неравенство:
5х^2-3х-2>0
Х1=-0,4; х2=1
(- ;-0,4)U(1;+ ) решение выше оси Ох
3.1. Значения функции положительны. У>0
участки графика лежат выше оси Ох
17.
12у
У>0
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
18.
3. Промежутки знакопостоянствау=5х^2-3х-2 график парабола, ветви вверх
Решите неравенство:
5х^2-3х-2<0
Х1=-0,4; х2=1
(-0,4;1) решение ниже оси Ох
3.2. Значения функции отрицательны. У<0
участки графика лежат ниже оси Ох
19.
12у
У<0
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
20.
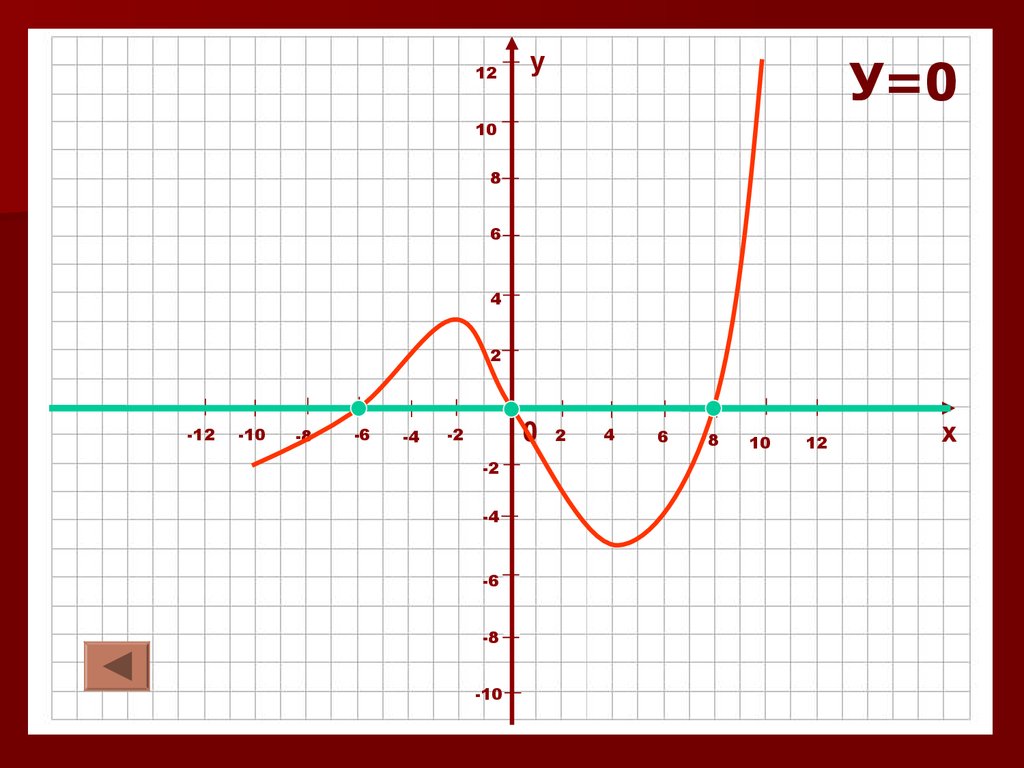
Промежутки знакопостоянства3.3. Значения функции равны нулю.
Нули функции - точки
пересечения с осями
т
координат
1) Пересечение с осью Ох: У=0 => (х;0)
2) Пересечение с осью Оу: Х=0 => (0;у)
*
Если функция задана формулой, то промежутки
знакопостоянства можно найти решив
неравенство или уравнение (для нулей
функции)
21.
12у
У=0
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
22.
4. Монотонность функциипромежутки возрастания и убывания функции
График «идет вверх/вниз» при движении слева направо по оси Ох
4.1. Функция называется возрастающей на
некотором промежутке, если большему
значению аргумента из этого промежутка
соответствует большее значение функции.
23.
Возрастающая функция.у
у2
у1
х1
х2
0
х
Х2>Х1 , то У2>У1.
-10
24.
4. Монотонность функциипромежутки возрастания и убывания функции
График «идет вверх/вниз» при движении слева направо по оси Ох
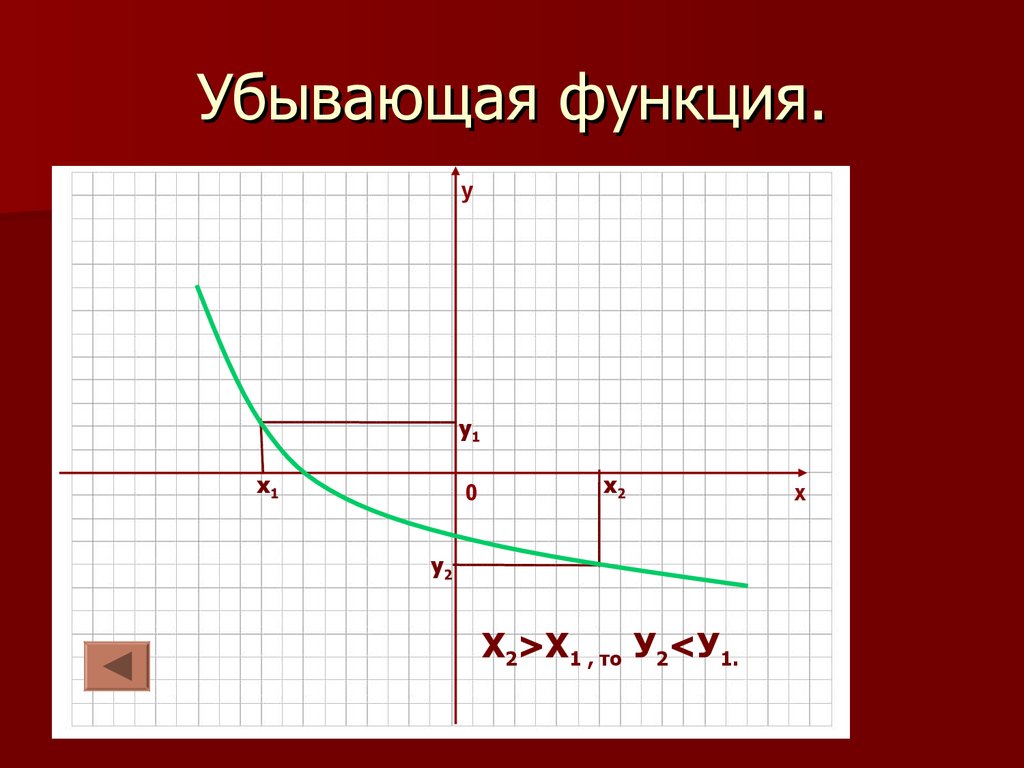
4.2. Функция называется убывающей на
некотором промежутке, если большему
значению аргумента из этого промежутка
соответствует меньшее значение функции.
25.
Убывающая функция.у
у1
х1
0
х2
х
у2
Х2>Х1 , то У2<У1.
-10
26.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
27.
5. Четные и нечетныефункции.
5.1. Функция у = f (x) называется четной, если
для всех х из области определения функции
для противоположных аргументов значения
функции одинаковые.
Выполняется равенство f (-x) = f (x).
График четной функции симметричен относительно оси Оу
28.
12у
f (-x) = f (x).
10
8
6
4
2
-12
-10
-8
-6
-х
-4
0
-2
-2
-4
-6
-8
-10
2
4
х
6
8
10
12
х
29.
5. Четные и нечетныефункции.
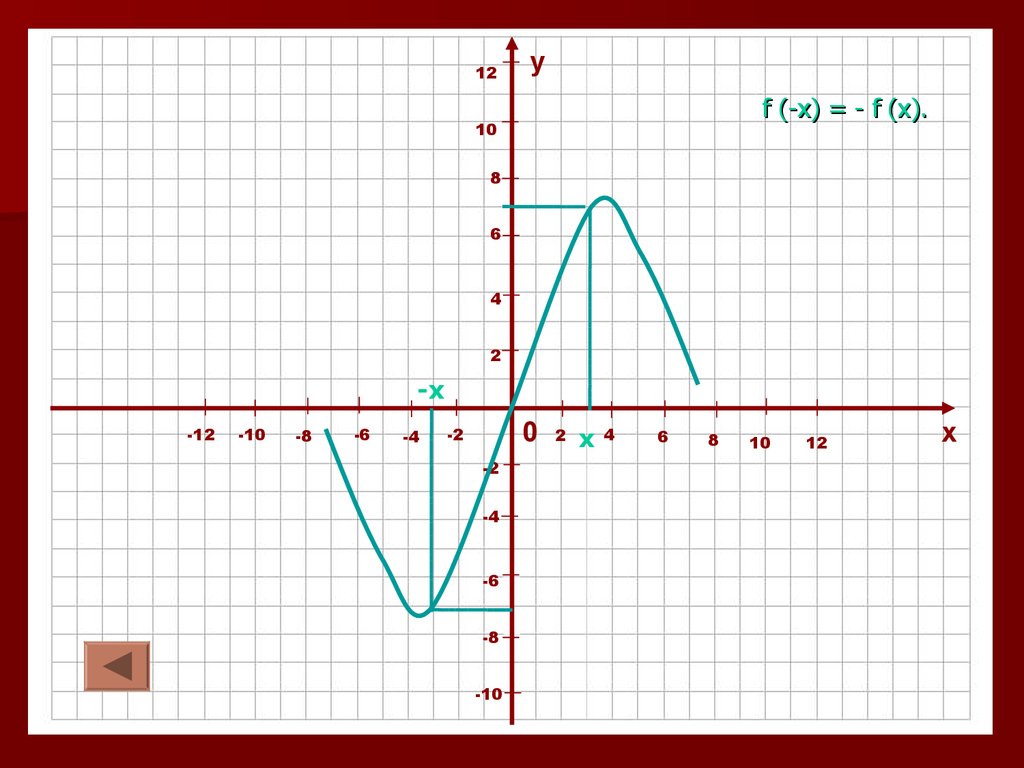
5.2. Функция у = f (x) называется нечетной,
если для всех х из области определения
функции для противоположных аргументов
значения функций противоположные.
Выполняется равенство f (-x) = - f (x).
График нечетной функции симметричен относительно начала координат
*
для того чтобы определить четность или нечетность функции по
формуле, вместо х подставить –х и выяснить знак выражения после
подстановки
№74 (а-г), 75(а-г)
30.
12у
f (-x) = - f (x).
10
8
6
4
2
-х
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
х
4
6
8
10
12
х
31.
6. Ограниченность функции.ограниченность функции можно посмотреть по области значений функции
6.1. Функция y=f (x) называется ограниченной
снизу, если для любого х из области
определения функции выполняется условие
f (x)≥a, где а – некоторое число.
График лежит выше прямой у=а
32.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
33.
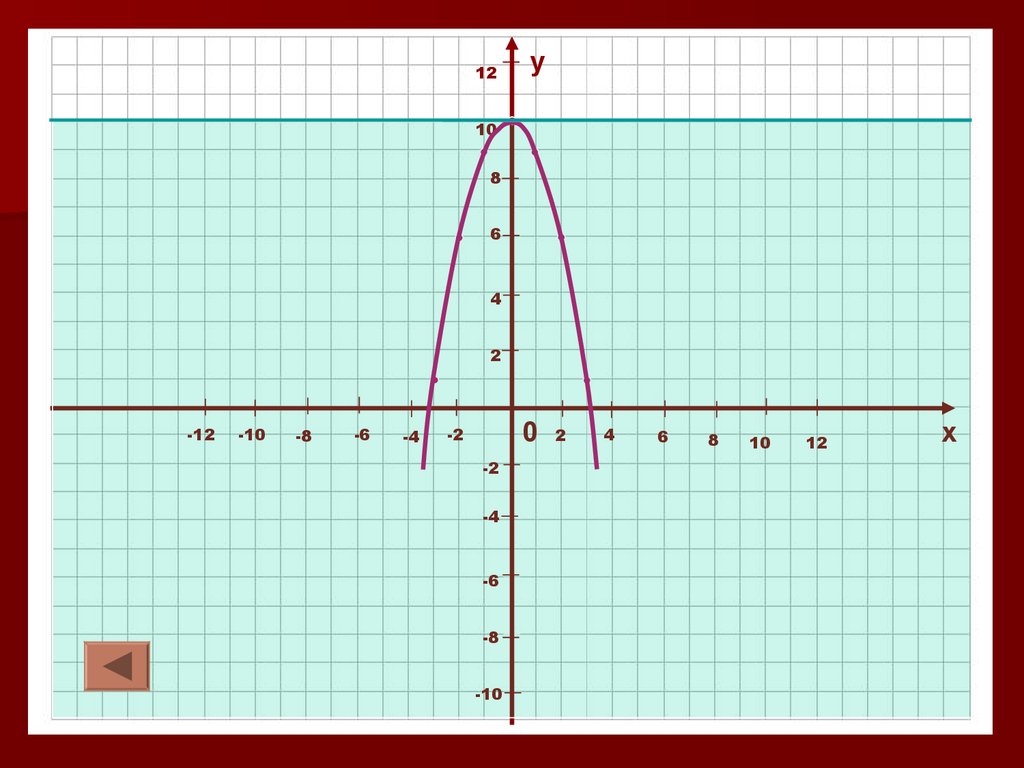
6. Ограниченность функции.6.2 Функция y=f (x) называется ограниченной
сверху, если для любого х из области
определения функции выполняется условие
f (x)≤ b, где b – некоторое число.
График лежит ниже прямой у=b
34.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
35.
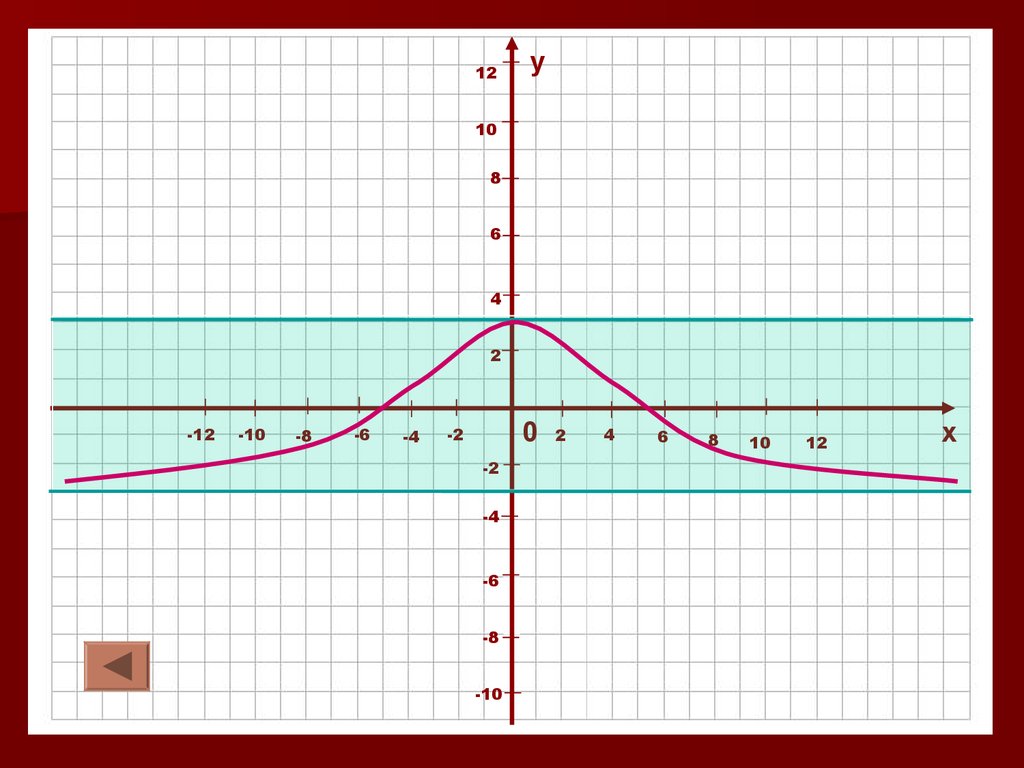
6. Ограниченность функции.6.3. Функция называется ограниченной, если
она ограничена и снизу, и сверху.
36.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
37.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
0
-2
-2
-4
-6
-8
-10
2
4
6
8
10
12
х
38.
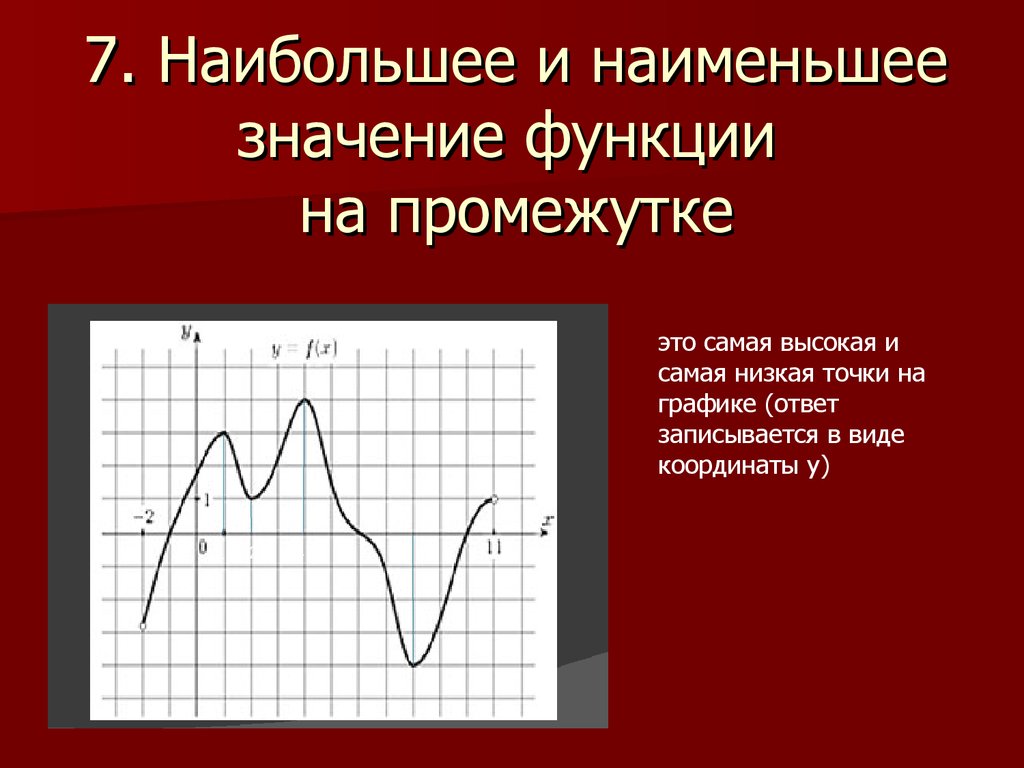
7. Наибольшее и наименьшеезначение функции
на промежутке
это самая высокая и
самая низкая точки на
графике (ответ
записывается в виде
координаты у)
39.
8. Точки максимума,минимума и перегиб.
(х;у)
Мах – самая высокая точка
Min – самая низкая точка
Перегиб – это волна или
резкая смена направления
40.
9. Непрерывность функции.Функция называется непрерывной, если у нее нет точек разрыва
41.
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИПрочитайте график функции:
1 вариант
2 вариант
4
4
2
2
1
1
-2
-2
-4
-4
42.
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИПрочитайте график функции:
1 вариант
2 вариант
1. Область определения функции
D(y) = (- ; + )
2. Область значений функции
E(y) = (-4 ; + )
E(y) = (- ; + )
3. Чётность/нечетность функции
Чётная
Нечётная
4. Нули функции
у=0 при х = 0; ±1,4
у=0 при х = 0; ±1,2
5. Промежутки возрастания/
убывания функции
y при х [–1;0], [1;+ ]
y при (– ;–1], [1;+ ]
y при x (– ;-1], [0;1]
y при х x [–1; 1]
6. Наибольшее/наименьшее
значение функции
унаим = –4; унаиб не сущ.
Унаим , унаиб не сущ.
7. Ограниченность функции
Ограничена снизу
Не ограничена
8. Непрерывность функции
непрерывна


































 mathematics
mathematics








