Степенная функция

1.

Степенная
функция

2.

Определение.
Определение Функцию вида
n
y x , n 2,...
называют степенной функцией
с натуральным показателем

3.

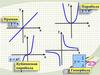
Нам знакомы функции
у
у=х
у = х2
Прямая
Парабола
х
у
у = х3
1
у
х
у
х
у
Кубическая
Гипербола
парабола
х
х

4.

у = х,
у=х,
2
1
у
х
у=х,
3
Все эти функции являются частными
случаями степенной функции
у = хn, у = х-n
где n – заданное натуральное число
Свойства и график степенной функции
зависят от значения показателя n
Функция задана таблицей.
n
y x , n 1,2,...

5. Является ли функция, заданная формулой, степенной с натуральным показателем?

1
1) y x 5
2
Нет, это линейная функция
2)
y x 8x 3
Нет
y x
Нет, показатель степени -дробь
3)
4)
2
y x
1
3
2
1
5) y
x2
6)
7
y x 3
Да, n=2
Нет
Да, n=7

6.

y
у x
2
График функции
–
парабола
-1
0 1
x
у x
2

7.

Степенная функция,
где показатель – четное число

8.

y
у = х2
у = х4
у = х6
-1 0 1 2
x

9.

11
График функции кубическая парабола
y
у x
1
0 1
x
у x
3
3
ветви
кубической
параболы

10.

Степенная функция,
где показатель – нечетное
число

11.

y
Чем больше n,
тем «круче» ветви
направлены
вверх и вниз
у = х3
у = х5
у = х7
-1 0 1 2
x

12.

y
-1 0 1 2
Ответ: х = 1
x

13.

y
у = х6
у = (х-1)6 – 2
-1 0 1 2
Сдвиг графика
функции у = х6
вправо на 1 единицу
и вниз на 2 единицы.
x

14.

Свойства степенных функций
с натуральными показателями степени
у = х 2n , где n N
n четное
у
4
Область определения :(- ∞; + ∞)
Область значений: [0; + ∞)
3
Четность (нечетность):
у(-х) = у(х), четная
Промежутки
знакопостоянства:
2
(- ∞; 0) (0; + ∞)
у > 0 на
Возрастание (убывание):
1
х
0
-2
-1,5
-1
-0,5
0
-1
0,5
1
1,5
убывает на (- ∞; 0]
возрастает на [0; + ∞)
Особые точки:
2
(-1; 1), (0; 0), (1; 1)

15.

Свойства степенных функций
с натуральными показателями степени
у = х 2n+1 , где n N
n нечетное
у
2
Область определения : (- ∞; +
Область значений: (- ∞; +∞)
∞)
1,5
Четность (нечетность):
1
у(-х) = - у(х), нечетная
0,5
Промежутки
х
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
-0,5
-1
-1,5
-2
знакопостоянства:
у > 0 на
(0; + ∞)
у < 0 на
(- ∞; 0)
Возрастание (убывание): возрастает на (- ∞; +
∞)
Особые точки:
(-1; -1), (0; 0), (1; 1)

16.

ПРИМЕР 1. Дана функция f (х) = x3.
Вычислим выражение f(3) - 4f(2) + 7f(1).
Чтобы найти значение функции при
данном значении аргумента, надо
подставить этот аргумент в формулу,
задающую функцию, и выполнить
действия.
f(3) - 4f(2) + 7f (1) = 33 - 4 ∙23+ 7 ∙13 = 27 - 4∙8 +
+ 7∙ 1 = 27 - 32 + 7 = 2.

17.

Сравните числа: a)(-3,2)4 и (-1,8)4; б) 2,44 и 2,74;
в) (-6,5)3 и (-4,8)3; г) 2,83 и 4,13.
При решении подобных задач учитывают монотонность
соответствующей функции.