Степенная функция

1.

2.

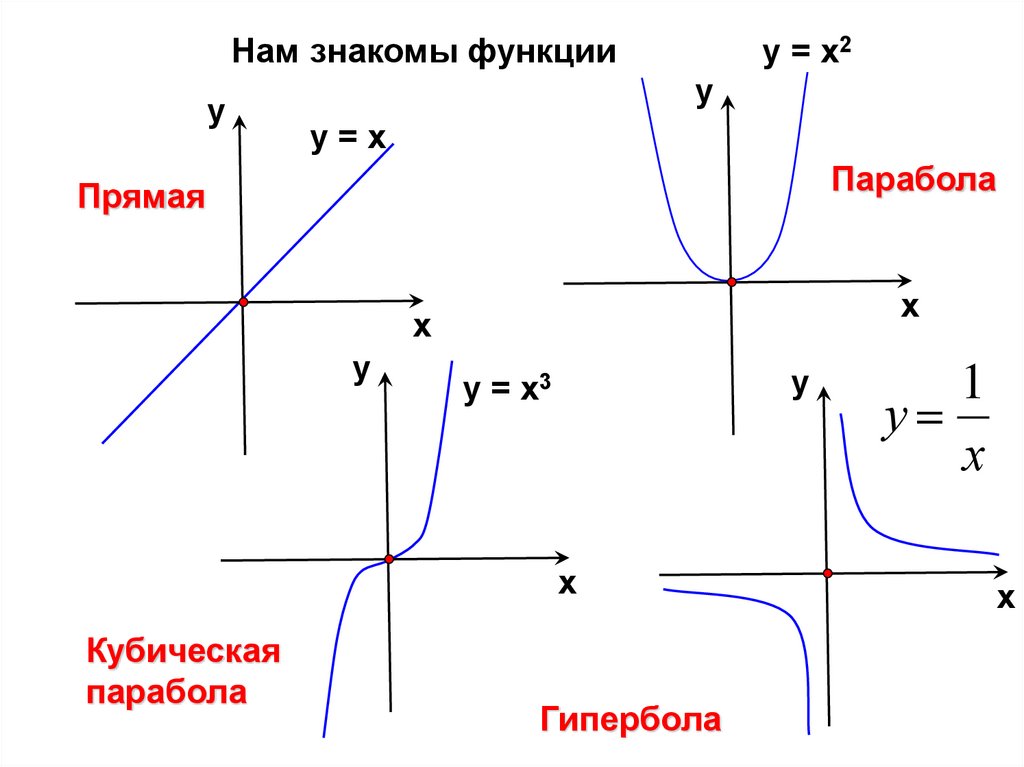
Нам знакомы функции
у
у = х2
у
у=х
Парабола
Прямая
х
х
у
у
у = х3
х
Кубическая
парабола
Гипербола
1
у
х
х

3.

у = х,
у = х2,
у = х3,
1
у
х
Все эти функции являются частными
случаями степенной функции
у = хr, где r – заданное действительное число
Свойства и график степенной функции
зависят от свойств степени с
действительным показателем, и в частности
от того, при каких значениях х и r имеет
смысл степень хr.

4.

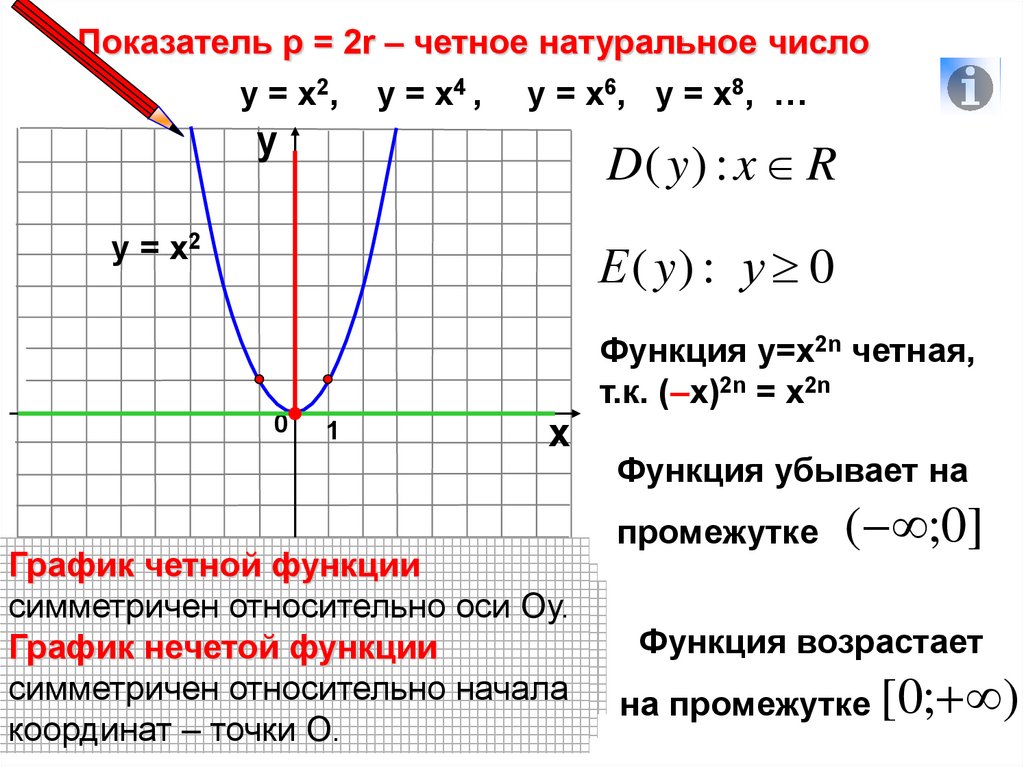
Показатель р = 2r – четное натуральное число
у = х2, у = х4 , у = х6, у = х8, …
у
D( y ) : x R
у = х2
Е ( y) : у 0
0
1
х
График четной функции
Область определения
значений
функции
симметричен
относительно
оси–Оу.–
Область
функции
множество
значений,
График
нечетой
функции
значения,
которые
может
которые может
принимать
симметричен
относительно
принимать
переменная
х начала
переменная
у О.
координат
– точки
Функция у=х2n четная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке [0; )

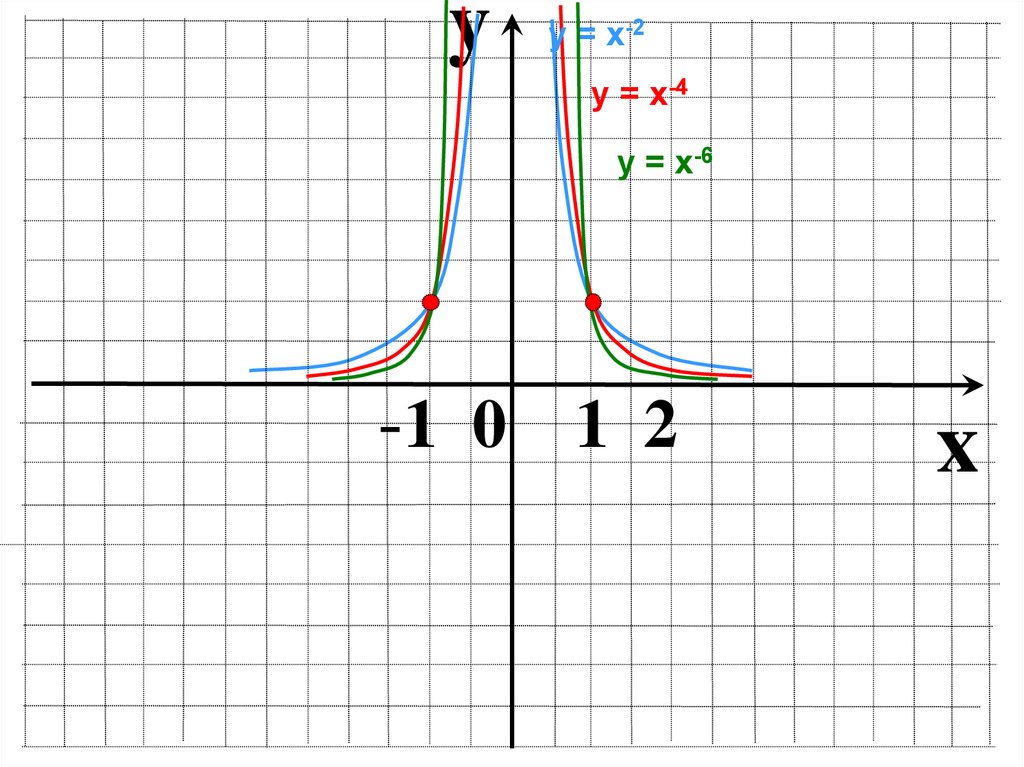
5.

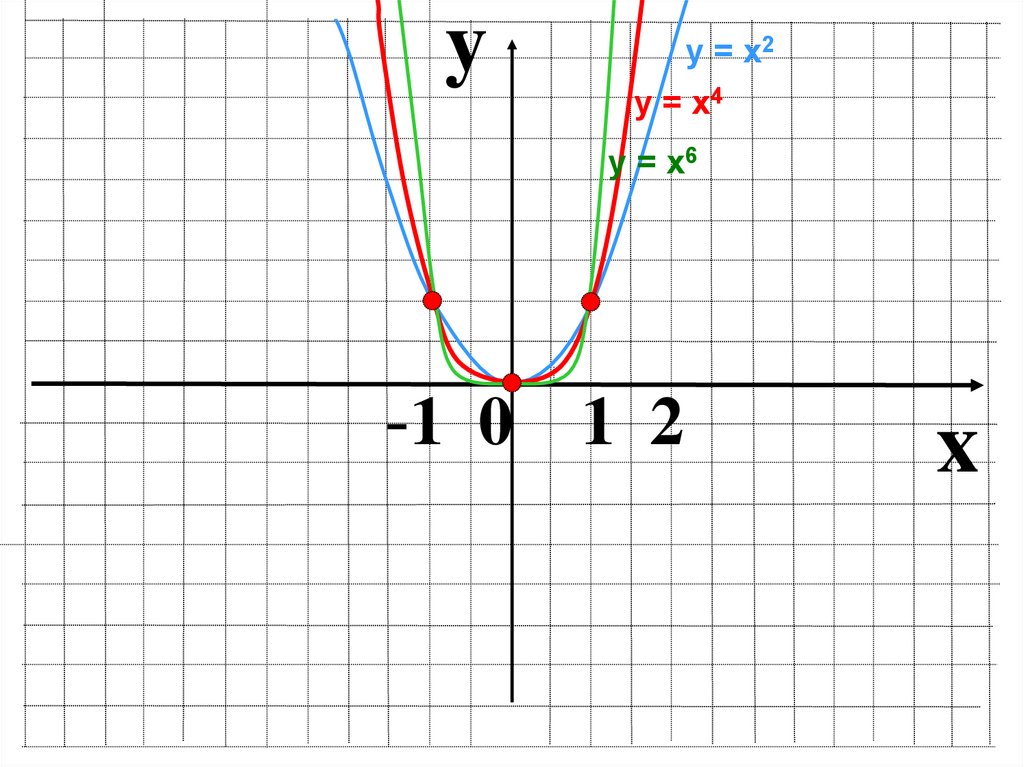
y
у = х2
у = х4
у = х6
-1 0 1 2
x

6.

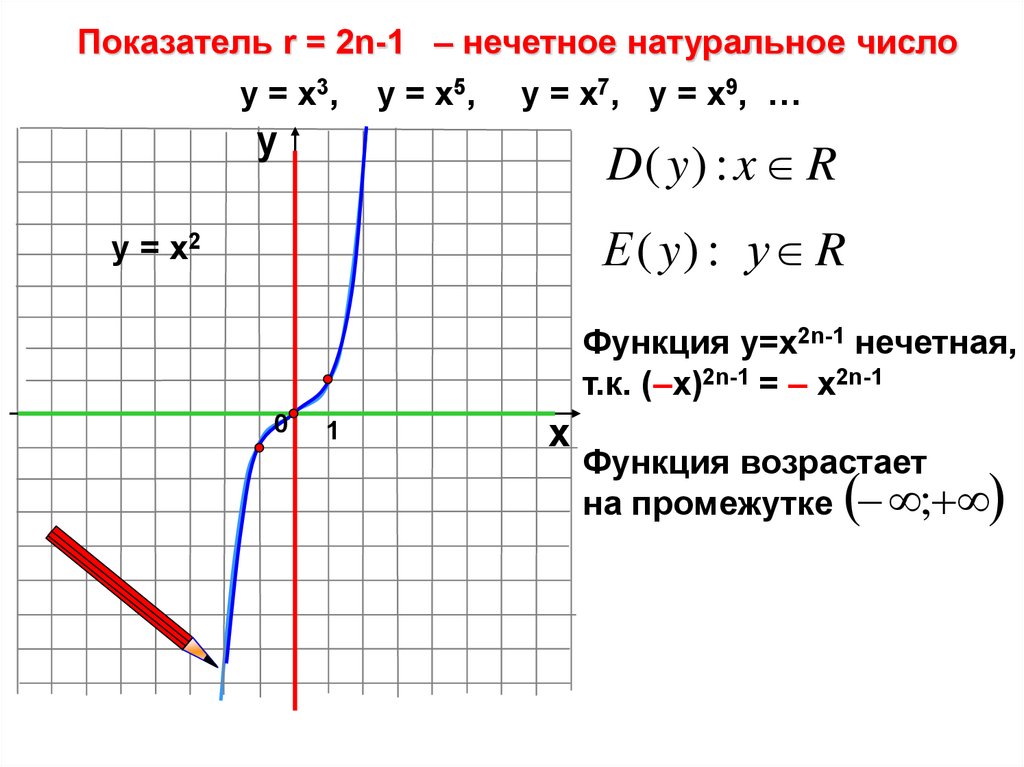
Показатель r = 2n-1 – нечетное натуральное число
у = х3, у = х5, у = х7, у = х9, …
у
D( y ) : x R
Е ( y) : у R
у = х2
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
1
х
Функция возрастает
на промежутке ;

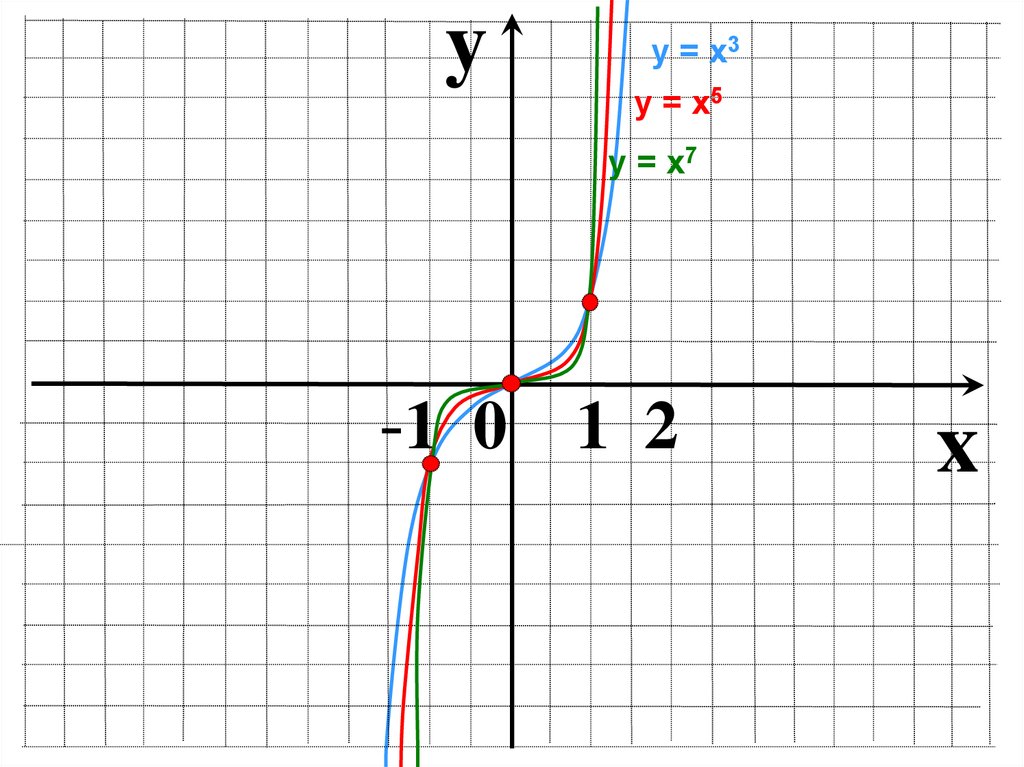
7.

y
у = х3
у = х5
у = х7
-1 0 1 2
x

8.

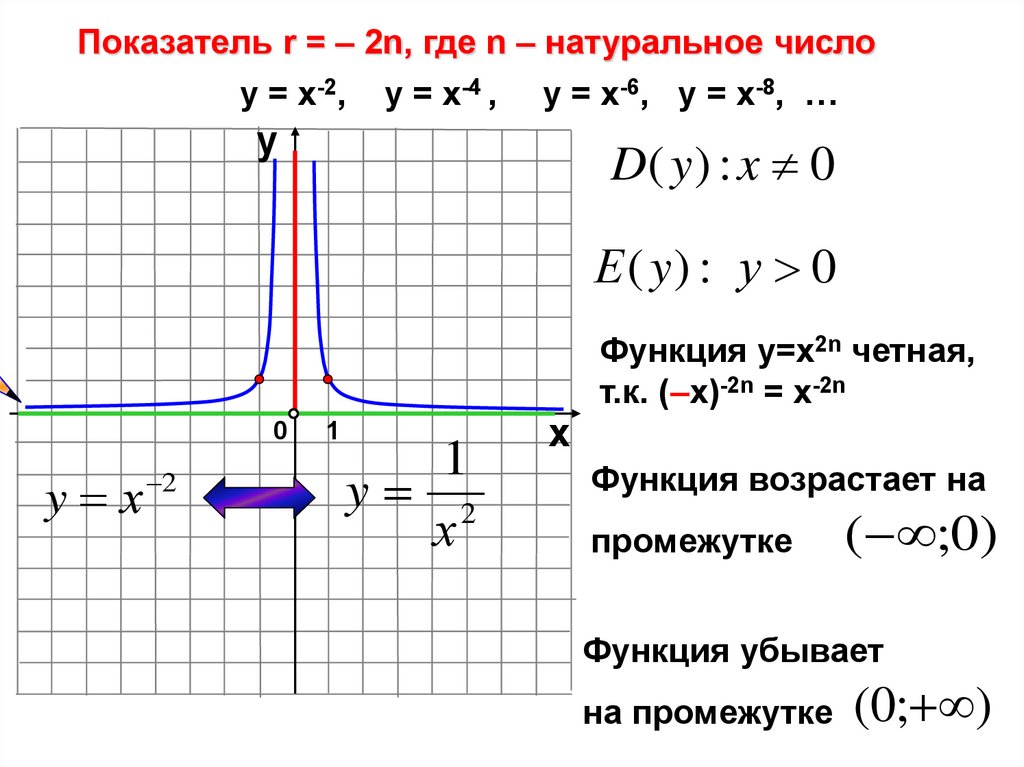
Показатель r = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2
1
1
y 2
х
х
Функция у=х2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке (0; )

9.

y у=х
-2
у = х-4
у = х-6
-1 0 1 2
x

10.

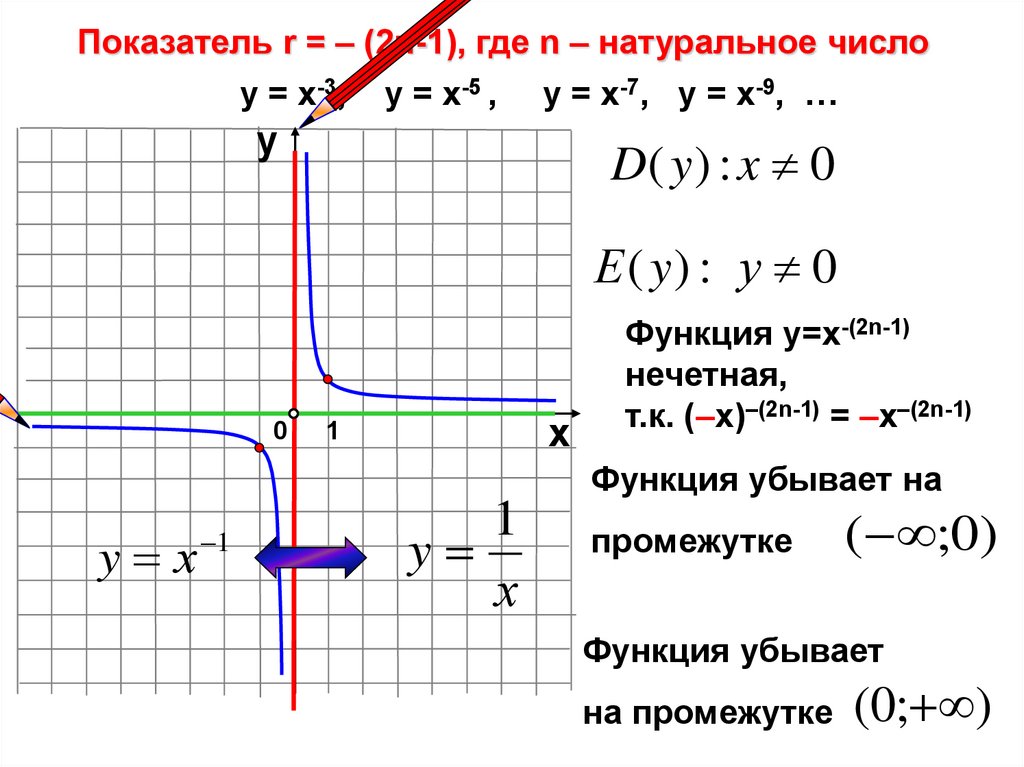
Показатель r = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
х
1
Функция у=х-(2n-1)
нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Функция убывает на
y х
1
1
y
х
промежутке
( ;0)
Функция убывает
на промежутке (0; )

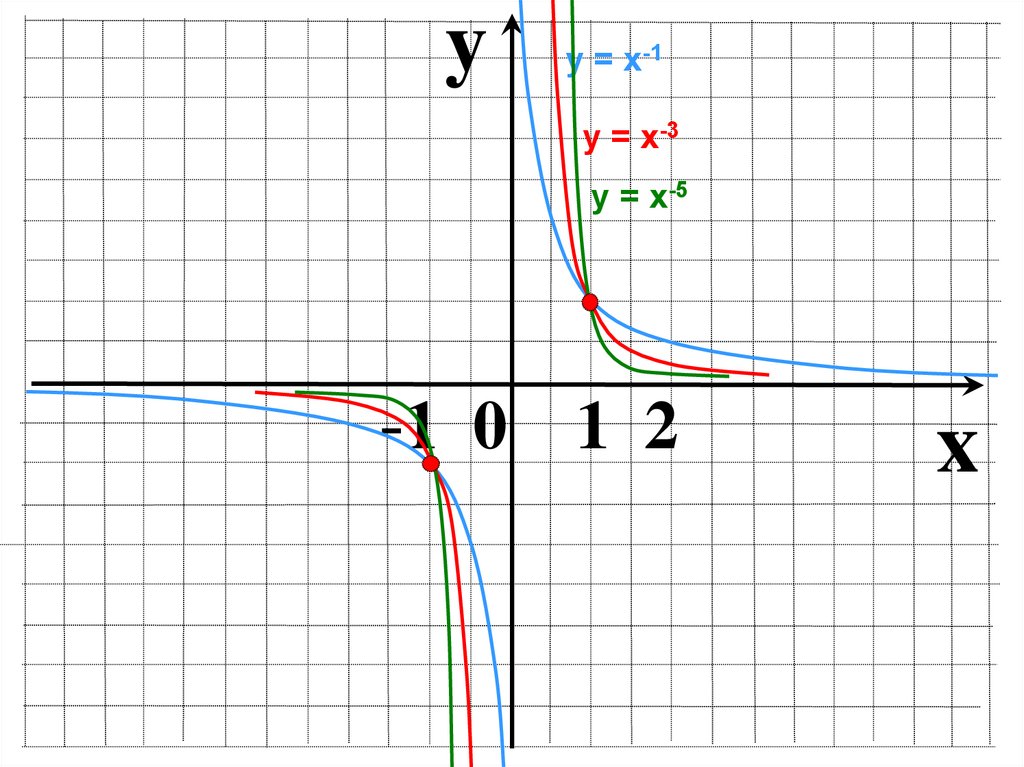
11.

y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x

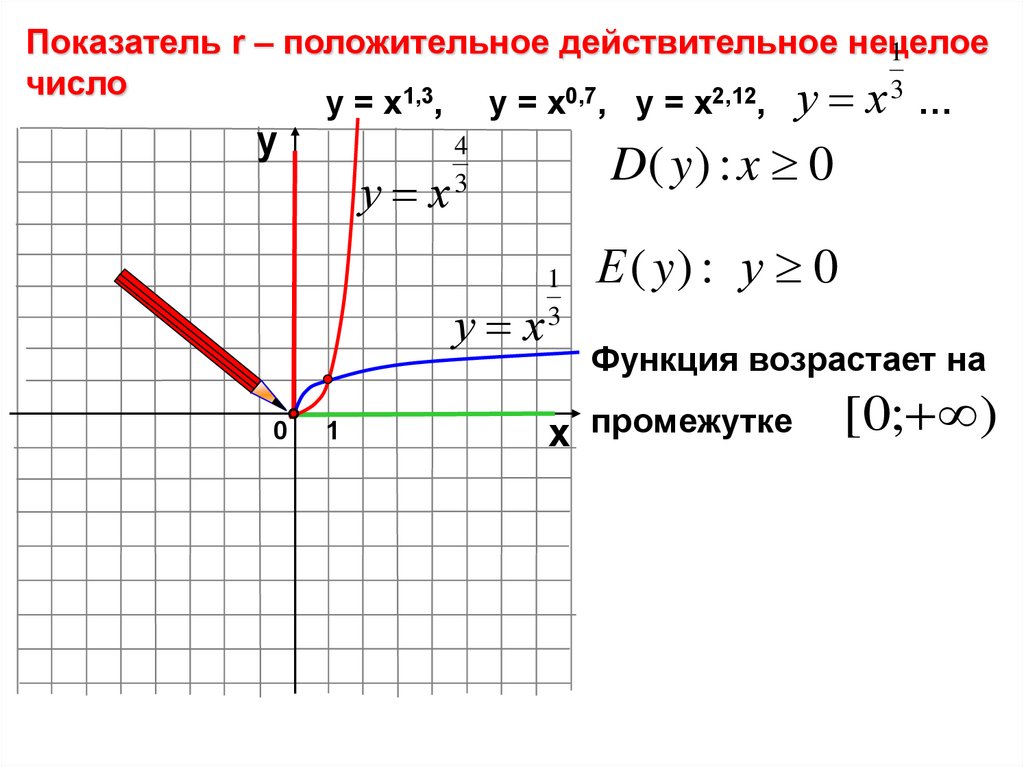
12.

Показатель r – положительное действительное нецелое
1
число
у = х1,3, у = х0,7, у = х2,12, у х 3 …
у
у х
у х
0
1
D( y ) : x 0
4
3
1
3
Е ( y) : у 0
Функция возрастает на
х промежутке
[0; )

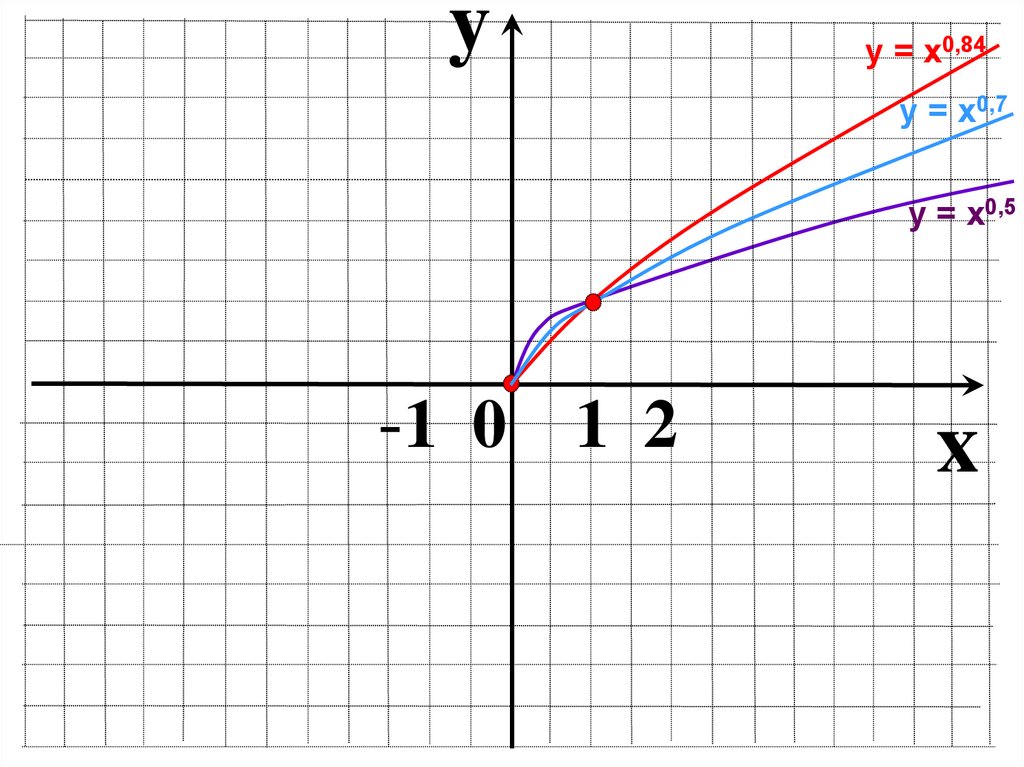
13.

y
у = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x

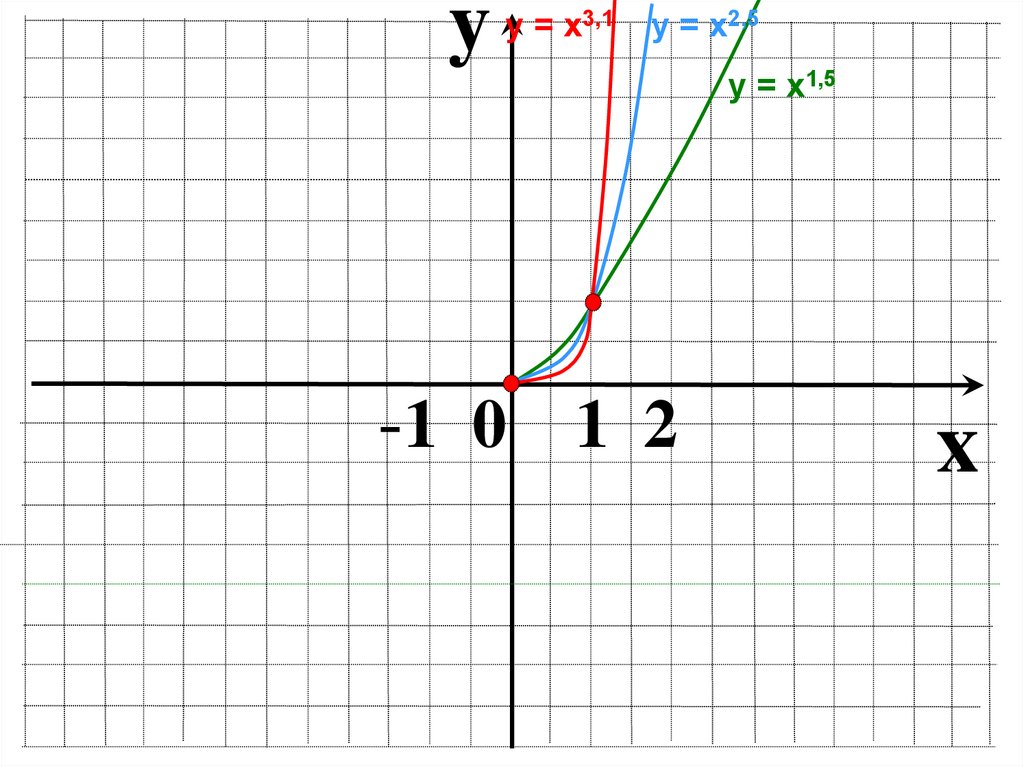
14.

y
у = х3,1
у = х2,5
-1 0 1 2
у = х1,5
x

15.

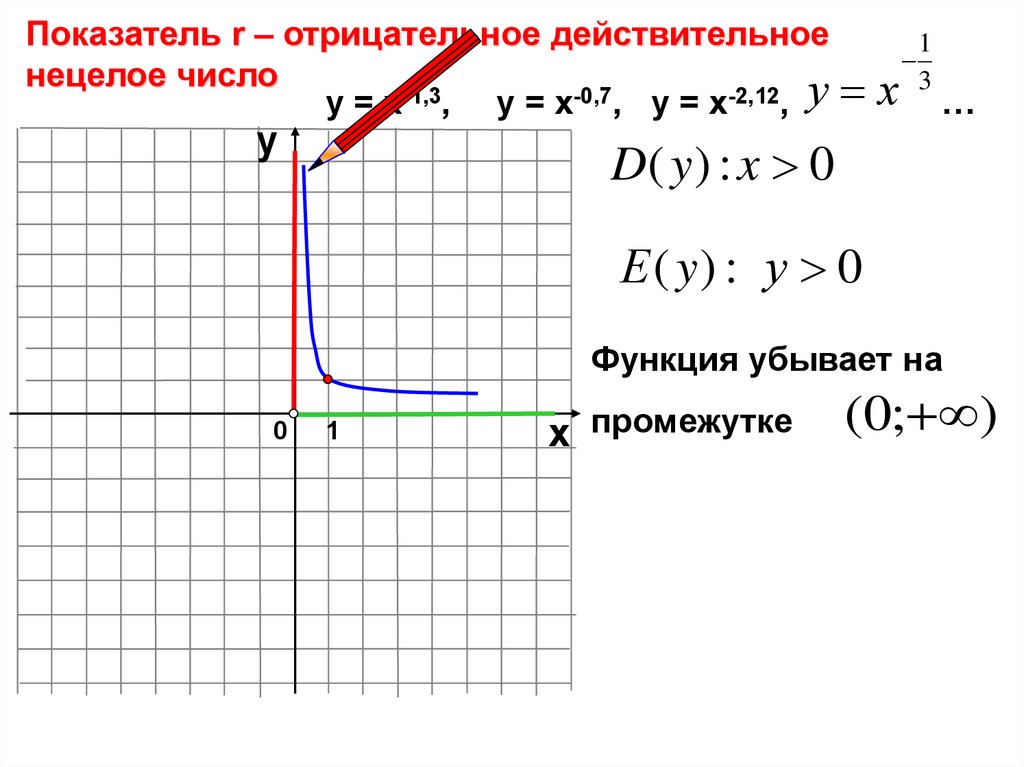
Показатель r – отрицательное действительное
1
нецелое число
3
-1,3
-0,7
-2,12
у
х
у=х , у=х , у=х
,
…
у
D( y ) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )

16.

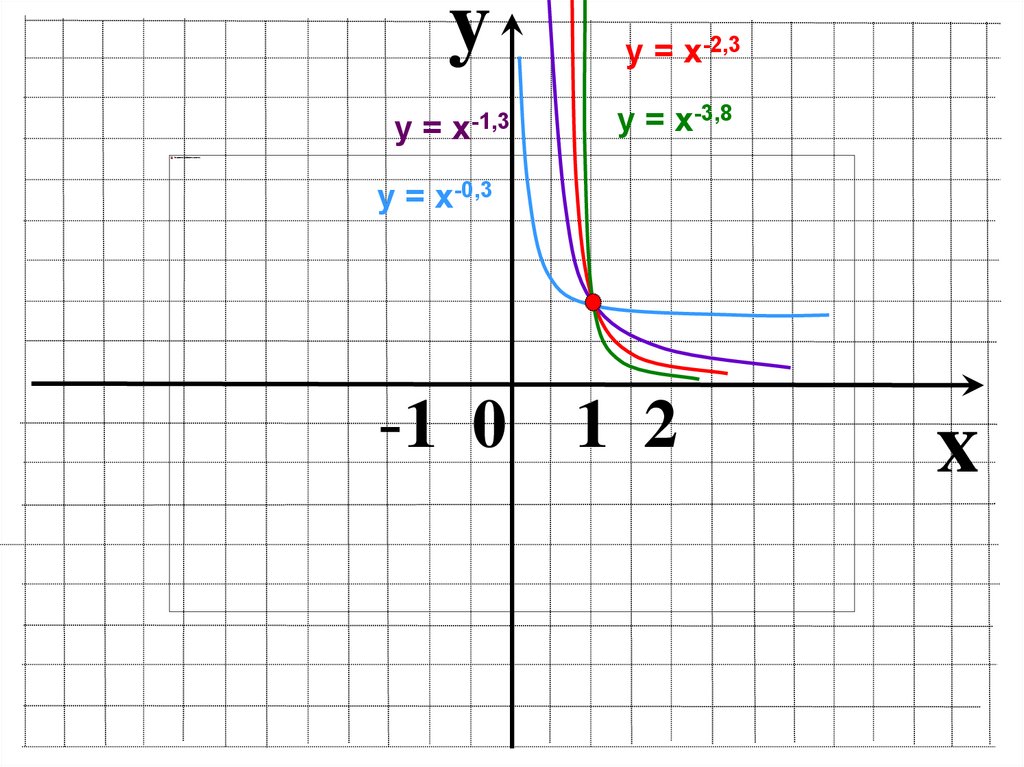
y
у = х-2,3
у = х-1,3
у = х-3,8
у = х-0,3
-1 0 1 2
x