Similar presentations:
Степенная функция
1.
9 классУчитель математики
Герасимова Т.Н.
ГОУ СОШ № 294
г.Санкт - Петербург
2.
График функцииУ = f (x)
Графиком функции называется множество точек
координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты соответствующим
значениям функции.
Теория
Практикум
Тренажер
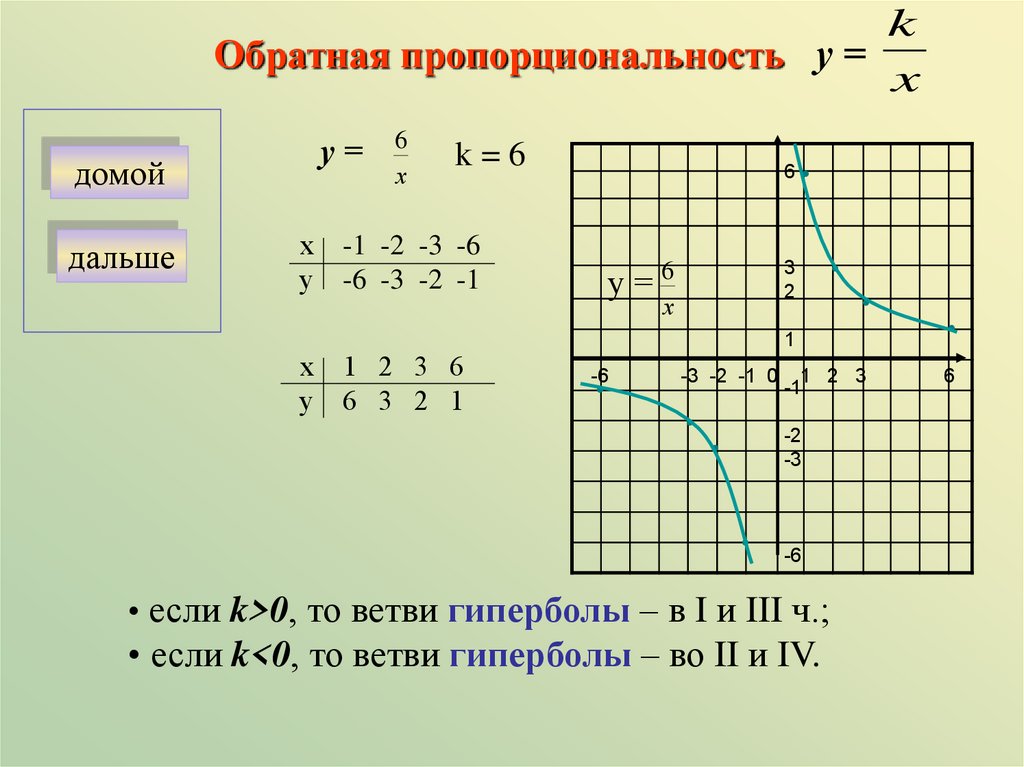
Обратная пропорциональность
3.
Определение степенной функцииp
Функция у = x , где р – заданное число,
называется степенной функцией.
Примеры:
y x
3
y x
1
2
y x
4
3
y x 5
• если р > 0, то степенная функция возрастает на промежутке х 0;
• если р < 0, то степенная функция убывает на промежутке х < 0.
4.
Название функцииВид
функции
Название
графика
Прямая
пропорциональность
у = kх
Прямая
Линейная
у = kх + b Прямая
Обратная
пропорциональность
Квадратичная
Кубическая
домой
k
y=
x
у = х²
у = х³
Гипербола
Парабола
Кубическая
парабола
5.
kОбратная пропорциональность у =
x
домой
дальше
у=
6
х
k=6
6
х -1 -2 -3 -6
у -6 -3 -2 -1
3
2
у=6
х
1
х 1 2 3 6
у 6 3 2 1
-6
-3 -2 -1 0
1 2 3
-1
-2
-3
-6
• если k>0, то ветви гиперболы – в I и III ч.;
• если k<0, то ветви гиперболы – во II и IV.
6
6.
Квадратичная функция у = х²назад
домой
дальше
у = х²
у
9
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
у=х²
Графиком квадратичной функции у
= х² является парабола, ветви
которой направлены вверх.
-3
4
• 1•
-2 -1 0
1 2 3 х
7.
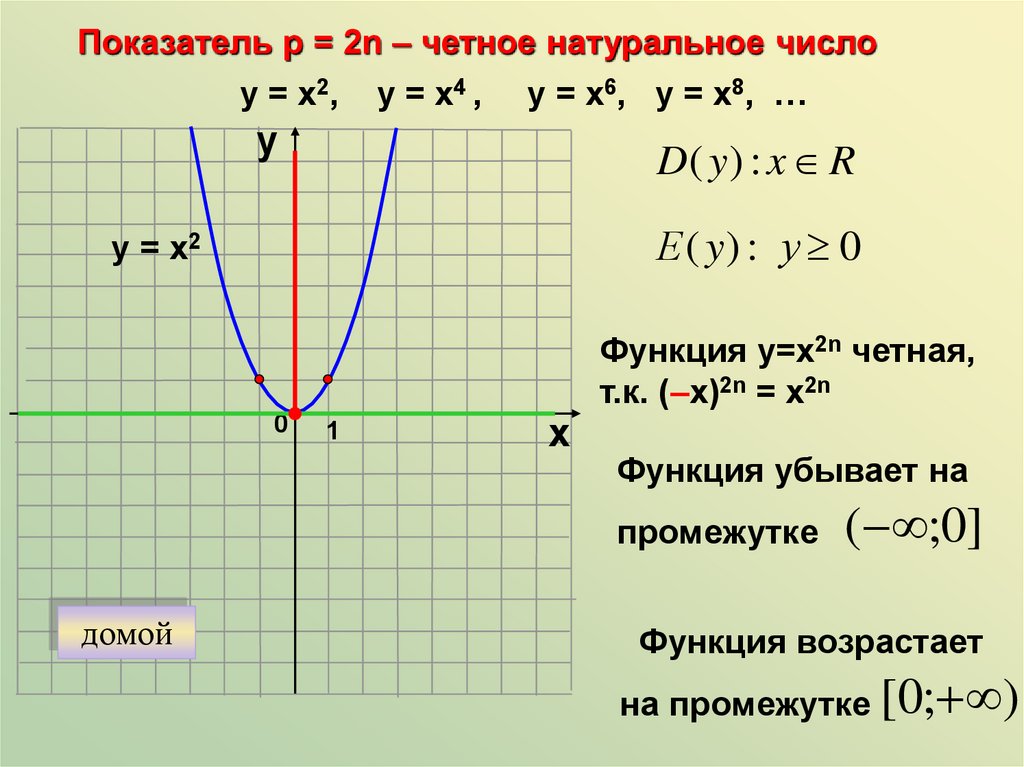
Показатель р = 2n – четное натуральное числоу = х2, у = х4 , у = х6, у = х8, …
у
D( y ) : x R
Е ( y) : у 0
у = х2
0
1
х
Функция у=х2n четная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
домой
( ;0]
Функция возрастает
на промежутке [0; )
8.
Показатель р = 2n-1 – нечетное натуральное числоу = х3, у = х5, у = х7, у = х9, …
у
D( y ) : x R
Е ( y) : у R
у = х2
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
1
х
Функция возрастает
на промежутке ;
домой
9.
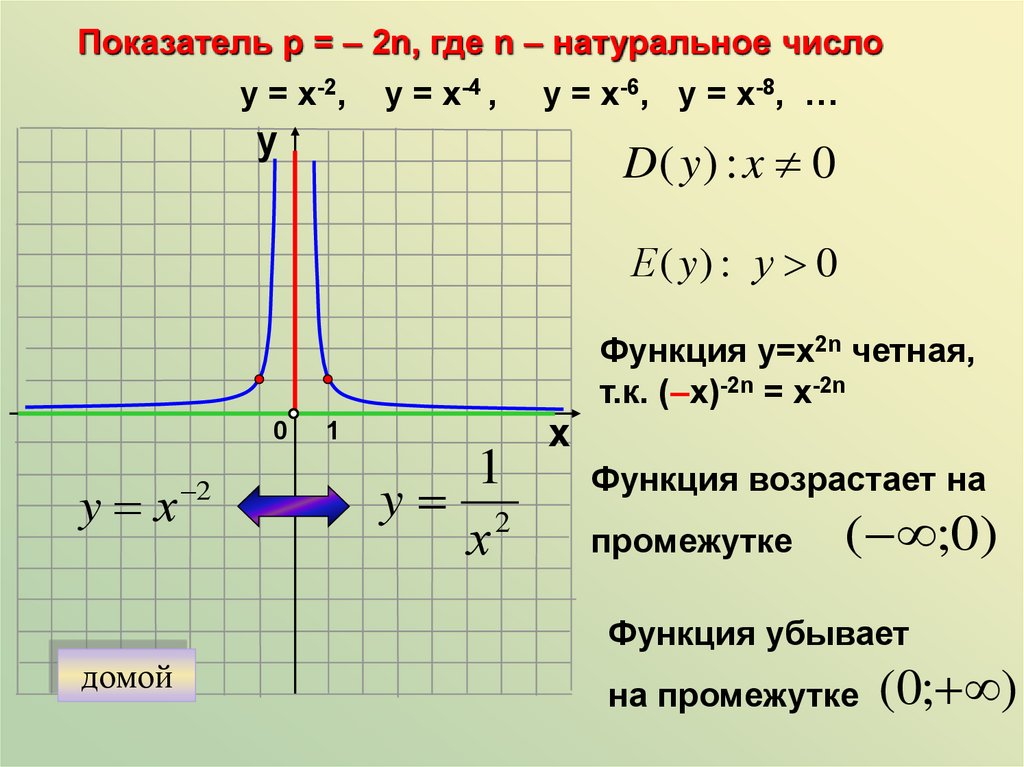
Показатель р = – 2n, где n – натуральное числоу = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2
1
1
y 2
х
х
Функция у=х2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
домой
на промежутке
(0; )
10.
Показатель р = – (2n-1), где n – натуральное числоу = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
домой
1
х
1
1
y
х
Функция у=х-(2n-1)
нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Функция убывает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
11.
Показатель р – положительное действительное нецелое1
число
у = х1,3, у = х0,7, у = х2,12, у х 3 …
у
у х
4
3
у х
0
1
D( y ) : x 0
1
3
Е ( y) : у 0
Функция возрастает на
х промежутке
[0; )
домой
12.
Показатель р – отрицательное действительноенецелое число
у = х-1,3, у = х-0,7, у = х-2,12, у
у
х
1
3
…
D( y ) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )
домой
13.
ПрактикумI вариант
домой
дальше
II вариант
1. Постройте график
функции у = х
1. Постройте график
2. Определите по
графику значение у
2. Определите по
графику значение у
при х = 0,5;1,5; 6,5; 7,2.
при х = 2; -2,5;- 4; 6.
3. Определите по
графику значение х,
соответствующее
значению у = 1; 4;6;9.
3. Определите по
графику значение х,
соответствующее
значению у = 8; -3; -2; 6.
функции у =
12
х
4. Найдите значение k, при котором точка А(k;1)
принадлежит данному графику.
14.
Тренажер1
Установите соответствие
между уравнением и
графической интерпретацией
2
6
х
3
4
6
5
= -3
1
2
3
4
5
6
х =1
1
2
3
4
5
6
х² = 4
1
2
3
4
5
6
- х = -2
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
х = -2
4
6
х
домой
=3
дальше
5
6
15.
Хотите продолжить?Да
Нет
домой
16.
Попробуйте ещёдомой














 mathematics
mathematics








