Similar presentations:
Степенная функция
1.
2.
Степенная функция её свойства и график.Вспомним функции
3. Определение степенной функции
• Степенная функция – это функция y= x p , где p –это заданное действительное число.
Свойства и график степенной функции существенно
зависят от свойств степени с действительным
показателем, и в частности от того, при каких
значениях x и p имеет смысл степень x p.
4.
yy=x4
y=x2
x
5.
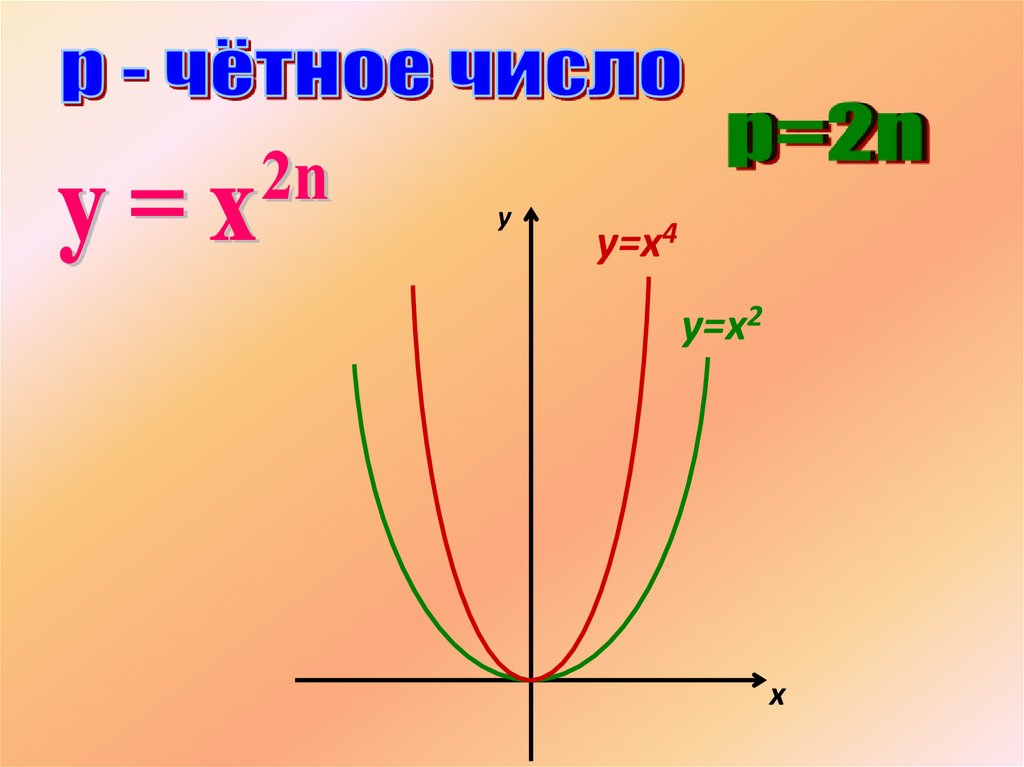
— область определения — вседействительные числа, т.е. множество R;
— множество значений — неотрицательные
числа, т. е. у ≥ 0;
— функция у = х2n четная, так как
(-х)2n = х2n;
y
y=x4
— функция является убываюy=x
щей на промежутке х ≤ 0,
2
возрастающей
на промежутке х ≥ 0.
x
6.
у0
х
7.
— область определения — вседействительные числа,
т.е. множество R;
— множество значений — все
действительные числа,
т.е. множество R;
— функция у = х2n-1 нечетная,
так как (-х)2n-1 = -х2n-1;
— функция является
возрастающей
на промежутке х € R.
у
0
х
8.
0< p <1y
y=x
1
0
1
1/3
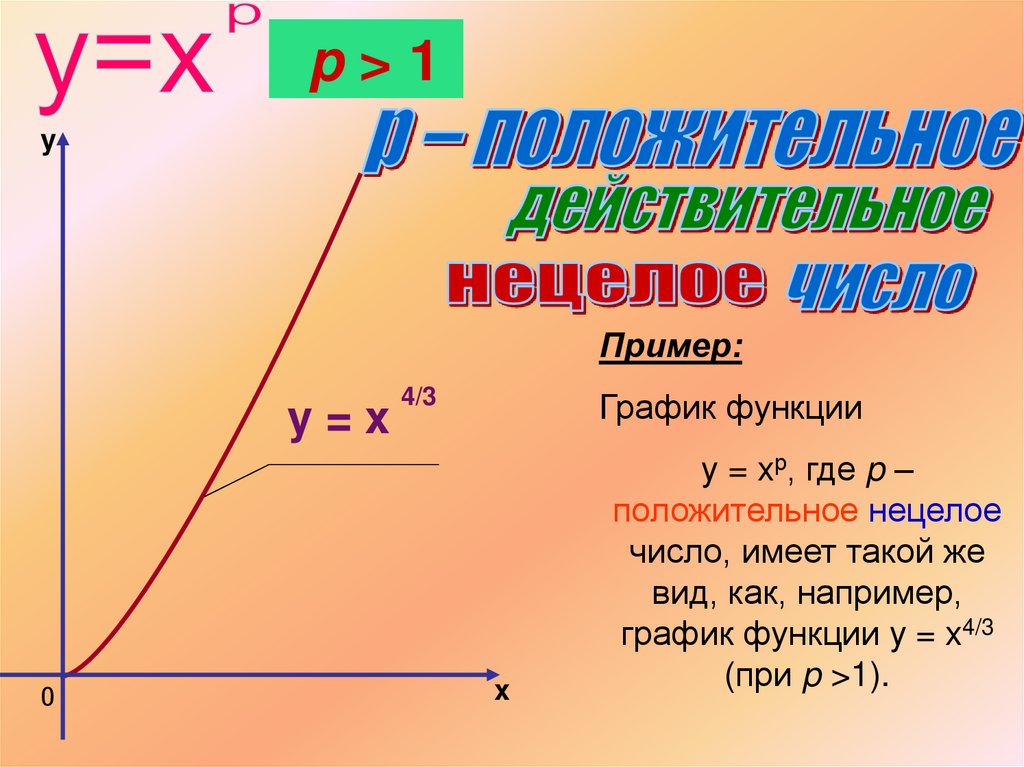
График функции y
= xр, где p –
положительное
нецелое число,
имеет такой же
вид, как,
например, график
функции
y = x1/3
x (при 0< p <1).
9.
р – положительное действительноенецелое число.
1. Область определения: Х ≥ 0
У≥0
3. Нули функции при х=0
2. Множество значений:
4. Функция является
возрастающей
на промежутке X ≥ 0
0< p <1
10.
p>1y
Пример:
y=x
0
4/3
График функции
x
y = xр, где p –
положительное нецелое
число, имеет такой же
вид, как, например,
график функции y = x4/3
(при p >1).
11.
p>11.Область
определения: x ≥ 0;
y
2.Множество
значений: y ≥ 0;
y=x
4/3
3. Нули функции при
х=0
0
4. Функция является
возрастающей на
x
промежутке x ≥ 0.
12.
p<013.
1. Область определения –положительные числа
x>0;
2. Множество значений –
положительные числа
y>0;
3. Нулей нет
4. Функция является убывающей
на промежутке
x>0.
p<0
14.
тест1.Степенной функцией называется функция вида:
2. Укажите номер рисунка, на котором 3. График, какой функции, изображён
изображен график нечётной функции.
на рисунке
1) y = x2n-1
2) y = x2n
3) y = x-2n
4) y = x-2n-1
15.
4.Укажите истинные утвержденияСтепенная функция у = х2n, где n - натуральное число, обладает
следующими свойствами:
1.
2.
3.
4.
5.
6.
область определения - все действительные числа, то есть множество R
множество значений - все действительные числа, то есть множество R
функция чётная
функция ограничена сверху
функция принимает наименьшее значение у = 0 при х = 0
функция является убывающей на промежутке х ≤ 0 и возрастающей на
промежутке х ≥ 0
5.Укажите истинные утверждения.
Степенная функция у = хр, где p- положительное действительное нецелое
число, обладает следующими свойствами:
1. область определения - все действительные числа, то есть множество R
2. множество значений - все действительные числа, то есть множество R
3. функция является возрастающей на промежутке х ≥ 0
4. функция не является ни чётной, ни нечётной
5. функция принимает наименьшее значение у = 0 при х = 0
16.
5. Изобразить схематично график функции, указать ее область определенияи множества значений:
1.
y=x6
2. y=x5
3. y=x1/2
6. Выяснить, является ли функция возрастающей или убывающей при х>0, если:
1.
p=4
2. p=16
3. p=-3









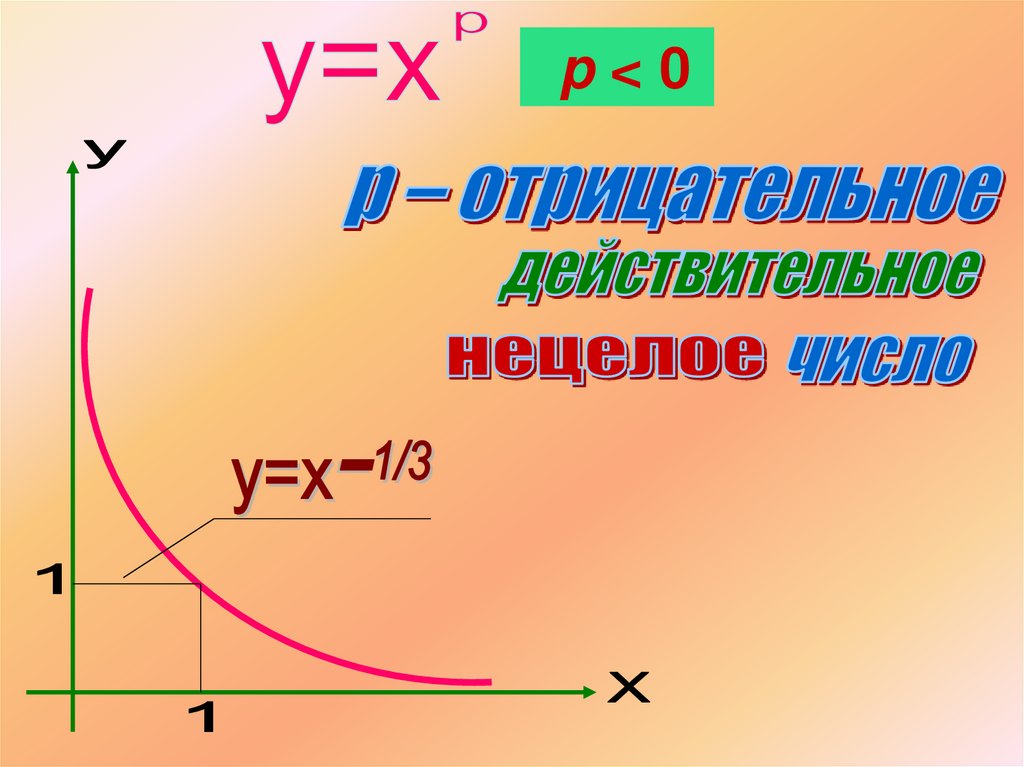




 mathematics
mathematics








