Кинематика плоских механизмов

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция №6
КИНЕМАТИКА ПЛОСКИХ МЕХАНИЗМОВ
§6.1 Примеры плоских механизмов
• Кривошипно-ползунный (шатунный). Croak rocker
(mechanism).
• Планетарный механизм - (motion less) gear
• Дифференциальный механизм - Drag – link- mech., –
equalizer.
• Эпициклический - epicycle gear
• Гипоциклический - hypocycloid gear
• Эллипсограф - trammel elliptic (mech.)
• Кулачковый механизм - cam (mech.)
I. Driving arbor output

3.

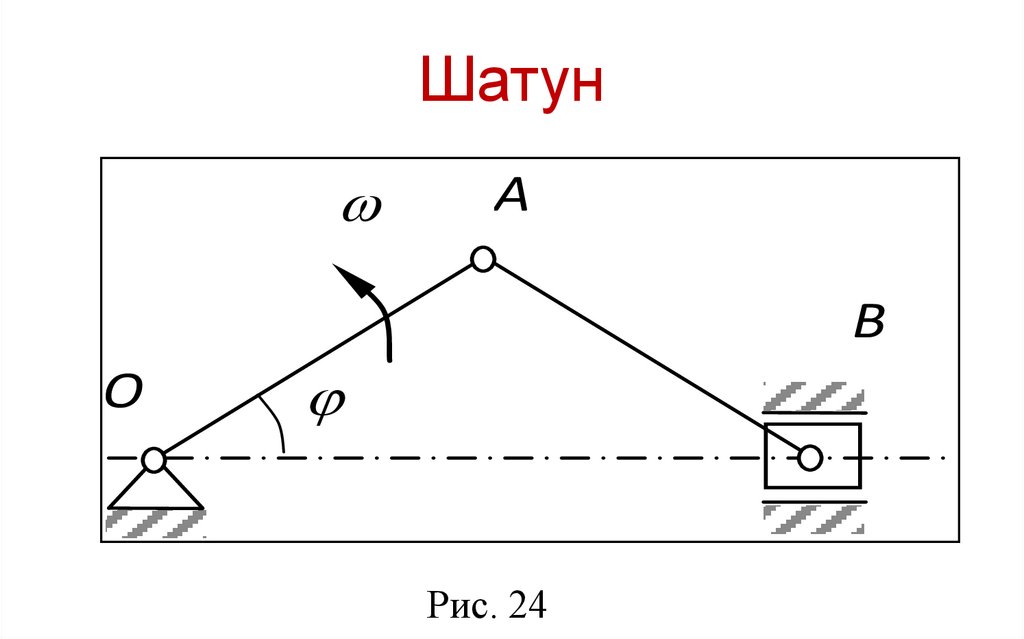
Шатун
А
В
О
Рис. 24

4.

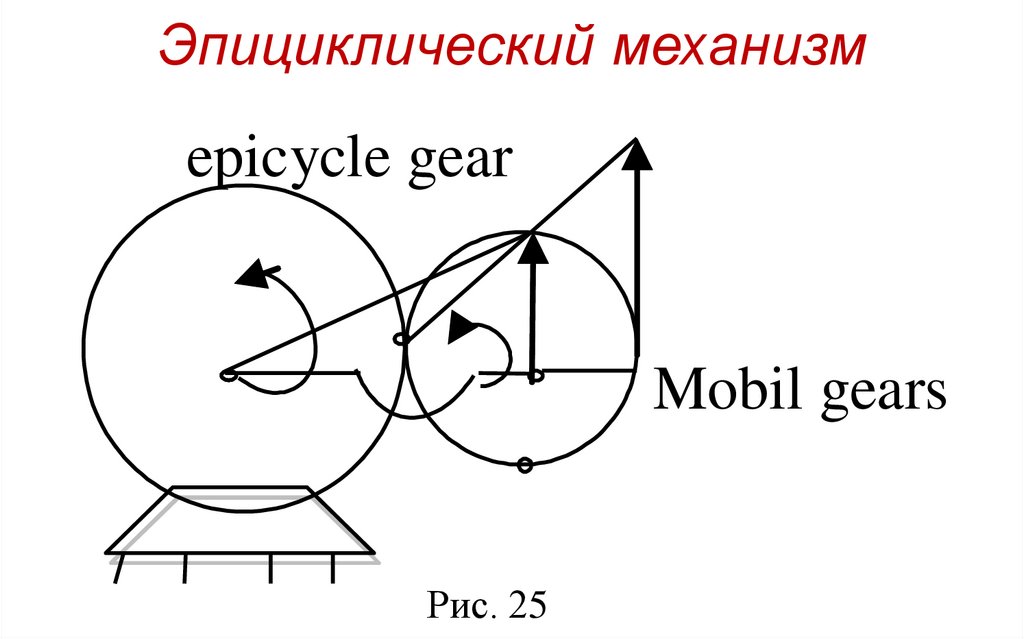
Эпициклический механизм
epicycle gear
Mobil gears
Рис. 25

5.

Гипоциклический механизм с
внутренним зацеплением
Рис. 26

6.

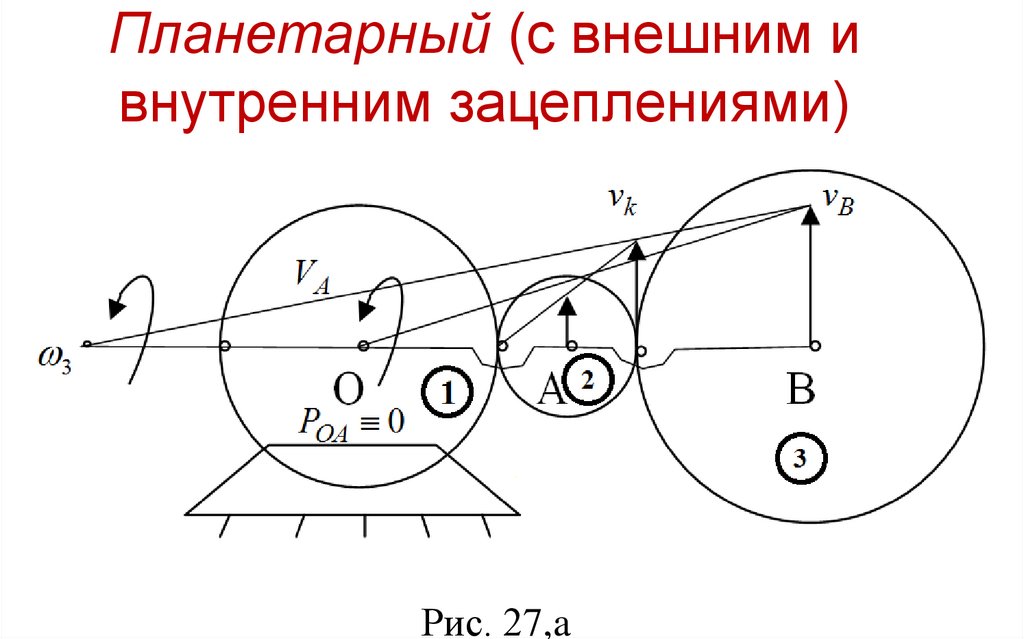
Планетарный (с внешним и
внутренним зацеплениями)
Рис. 27,a

7.

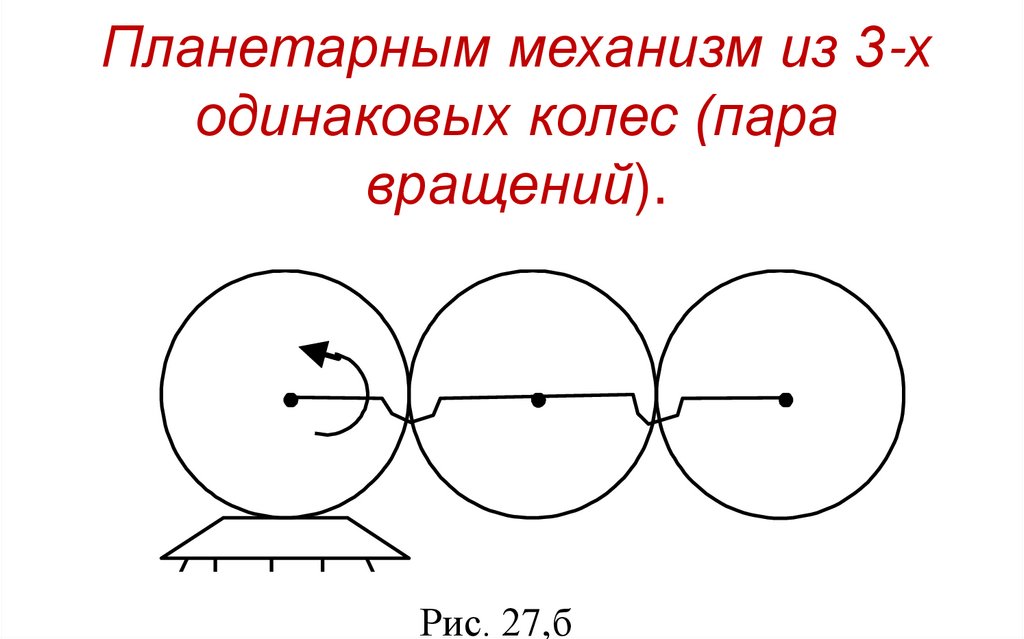
Планетарным механизм из 3-х
одинаковых колес (пара
вращений).
Рис. 27,б

8.

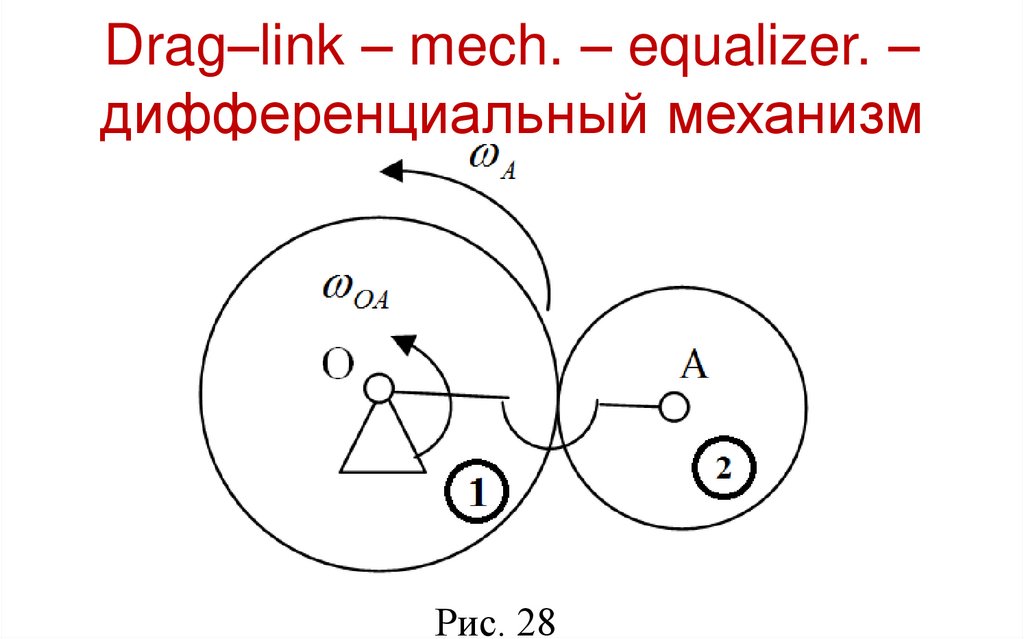
Drag–link – mech. – equalizer. –
дифференциальный механизм
Рис. 28

9.

VA
Пр ACV A
P2
A
2
B
OA
O
1
C
VC
3
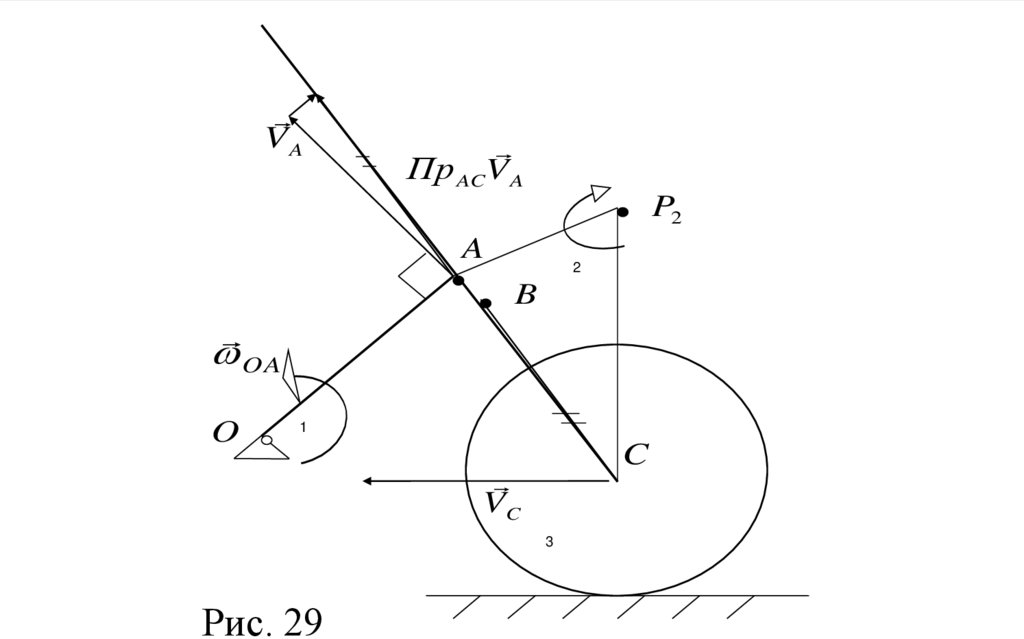
Рис. 29

10.

“Крестовая” формула для скоростей
точек плоской фигуры.
VA
AP
BP
VB VA
AP
VC
CP
VB
BP
VA
AP
VD
VB
DP
BP

11.

§6.2. Понятие о центроидах.
Введем понятие о центроидах. Оно активно используется в курсе ТММ
при решении задач, связанных с анализом и синтезом эквивалентных
механизмов. Дадим определения:
Геометрическое место точек МЦС в подвижной
плоскости называется подвижной центроидой.
Геометрическое место точек МЦП в неподвижной
плоскости называется неподвижной центроидой.
В данной лекции ограничимся только определениями, формулировкой
одной теоремы и одним примером. Доказательство теоремы и другие
примеры законспектируете из учебника (см. календарный план).
Теорема: Плоское движение твердого тела можно
представить как качение без проскальзывания подвижной
центроиды по неподвижной.

12.

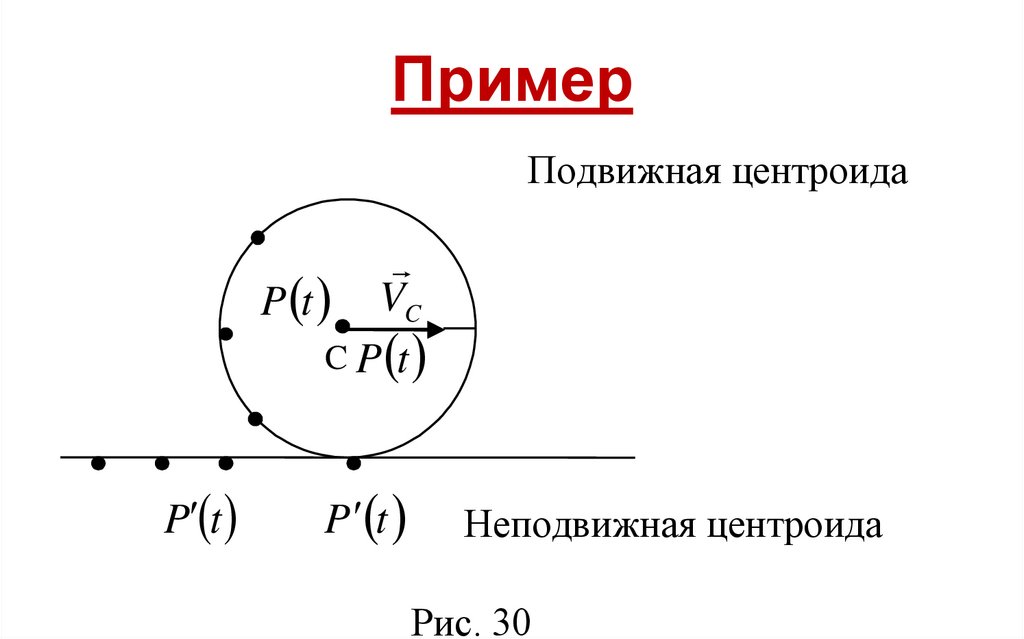
Пример
Подвижная центроида
P t VC
C P t
P t
P t
Неподвижная центроида
Рис. 30