1.3 УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ. СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ.

594.00K

Category:

physics

Кинематика

1.

1. КИНЕМАТИКА
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Кинематикой называют раздел механики, изучающий способы (не
причины!) описания движений и связь между величинами,
характеризующими эти движения.
МОДЕЛИ МЕХАНИЧЕСКИХ СИСТЕМ:
Материальная точка (МТ) – любой объект, формой и размерами
которого в данной задаче (в данных условиях) можно пренебречь;
Набор конечного числа материальных точек – достаточно общая
модель произвольной механической системы.
Абсолютно твёрдое тело (АТТ) – тело, форма и размеры которого
при наличии тех воздействий, что описаны в условиях задачи, могут
считаться неизменными. АТТ можно рассматривать как набор
материальных точек с неизменными расстояниями между ними.
Тело отсчёта, жёстко связанная с ним система координат и часы
образуют систему отсчёта (СО).

2.

Y
0
X
Z
K
Рис.1.1
О – начало координат (начало отсчёта); K – название системы отсчёта.
Положение МТ в пространстве в определённый момент времени задаётся
тремя её координатами (например, декартовыми,) или радиус-вектором :
(1.1)
rx x , ry y , rz z .
r r (t ) :
При движении МТ её координаты становятся функциями времени:
x x(t ) , y y (t ), z z (t ) .
(1.1 а, б, в)
Закон движения МТ– правило, по которому можно определить её положение в
любой момент времени.
P.S. Закон движения (1.1 а, б, в) можно рассматривать как уравнения
траектории, заданной в параметрическом виде (в роли параметра - t).

3.

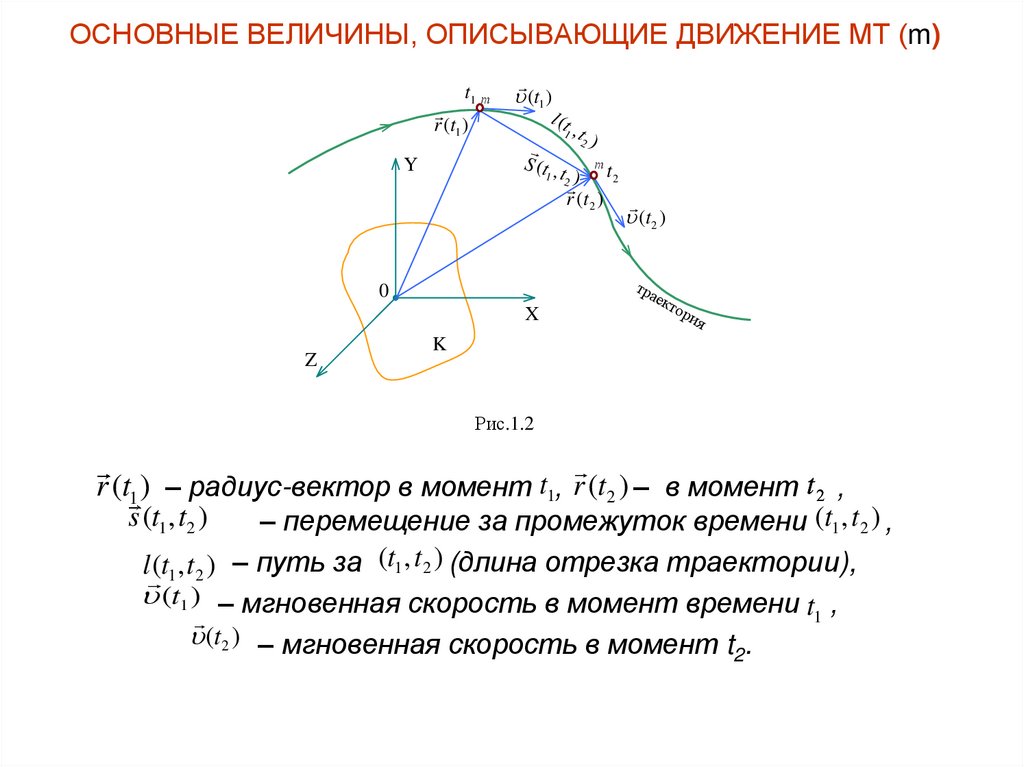
ОСНОВНЫЕ ВЕЛИЧИНЫ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ МТ (m)
t1 т
r (t1 )
Y
(t1 )
l (t
1 ,t
2)
т
S (t , t
t2
1 2)
r (t 2 )
(t2 )
0
X
Z
тр а
ект
ор
ия
K
Рис.1.2
t
r
r (t1 ) – радиус-вектор в момент 1, (t2 ) – в момент t 2 ,
s (t1 , t2 )
– перемещение за промежуток времени (t1 , t 2 ) ,
l (t1 , t 2 ) – путь за (t1 , t 2 ) (длина отрезка траектории),
(t1 ) – мгновенная скорость в момент времени t ,
1
(t2 ) – мгновенная скорость в момент t .
2

4.

PS. Векторы скорости (t1 ) и (t2 ) – касательные к траектории.
Очевидно:
s (t1 , t 2 ) r (t 2 ) r (t1 ) r
.
При малых t t2 t1 очевидно, что
s (t1, t2 ) l (t1, t2 ) .
Средняя скорость
s (t1,t2 ) Δr
υср(t1,t2 )
t2 t1
Δt .
Мгновенная скорость
r
(t ) lim ср ( t, t t ) lim .
t 0
t 0 t
(1.2)
или («точка» обозначает производную по времени)
dr .
(t )
r
dt
Средняя путевая скорость
ср ( )
l( t1 ,t2 ) l
t2 t1
t
(1.3)
,
(1.4)
l l (t2 , t1 ) – путь, пройденный за t t2 t1 . При t 0 получаем:

5.

Мгновенная путевая скорость (при t 0 ):
Или
l .
t 0 t
dl
( )
.
dt
( ) lim
(1.5)
Среднее ускорение за промежуток времени (t1 , t 2 ) :
υ (t 2 )-υ (t1 )
aср (t1 ,t 2 )
.
t 2 -t1
t
Мгновенное ускорение (в момент t ) :
d
a (t )
dt
Очевидно:
d 2 r
a r 2
dt
(1.6)
.
(1.7)
.
(1.8)
r
PS.1 Если закон движения задан, например, известна зависимость (t ) , то
мы имеем о движении полную информацию, и все величины,
определённые равенствами (1.3) – (1.8) легко вычисляются, точно так же,
как и их проекции на декартовы оси.
r (t ) (t )
PS.2 Переход
и
выполняется с помощью
(t ) a (t )
дифференцирования, а обратно с помощью интегрирования.

6.

Чтобы найти r (t ) по заданной (t ) , необходимо нач. значение
t
t
r (t ) r (0) (t ' )dt ' r0 (t ' )dt ' .
0
0
Аналогично:
t
t
(t ) (0) a (t ' )dt ' 0 a (t ' )dt ' .
В координатной форме:
0
0
x
( x )ср
t
x
x
t
ax
( a x )ср
r0 r (0) ;
(1.9)
(1.10)
dx
dt
d x
dt
Пример . (из школьной жизни!). Прямолинейное равноускоренное движение.
2as 2 0 2 ;
s 0t at 2 2;
0 at ;
a const.
Очевидно, что
s (t );
a (t ) s (t ).

7.

1.2. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ:
ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ.
d
a (t )
.
dt
Итак
Очевидно, при криволинейном движении ускорение материальной точки отлично от
нуля, т.к. вектор скорости изменяется по величине и по направлению.
Представим вектор скорости в виде:
1
т.е. – единичный вектор, направленный по скорости
(1.11)
.
Продифференцируем (1.11) и получим полное ускорение в виде 2-х слагаемых:
d d
d
.
(1.12)
a
dt
dt
dt
Обозначим:
d
d
(1.13)
a
an
dt
dt
Итак, полное ускорение расщепляется на две составляющие:
a a an
(1.14)

8.

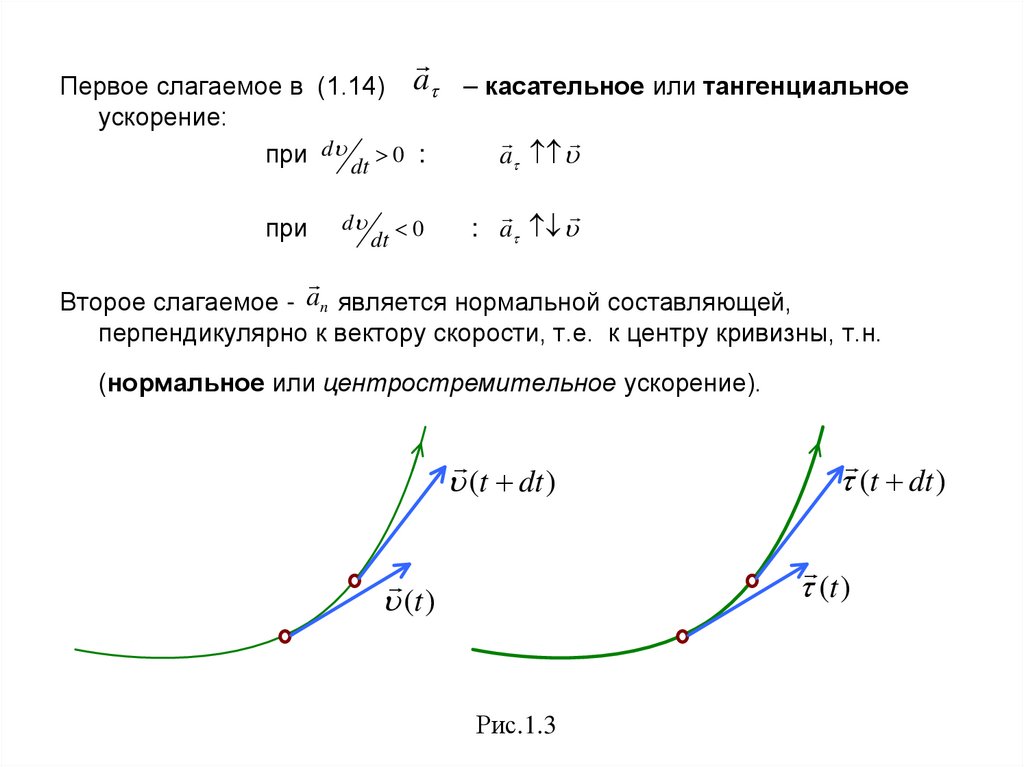
a
Первое слагаемое в (1.14)
ускорение:
при d dt 0 :
при
d
dt
– касательное или тангенциальное
a
: a
0
a
Второе слагаемое - n является нормальной составляющей,
перпендикулярно к вектору скорости, т.е. к центру кривизны, т.н.
(нормальное или центростремительное ускорение).
(t dt )
(t dt )
(t )
(t )
Рис.1.3

9.

(t dt ) d
d
(t )
a
an
.
.
a
d
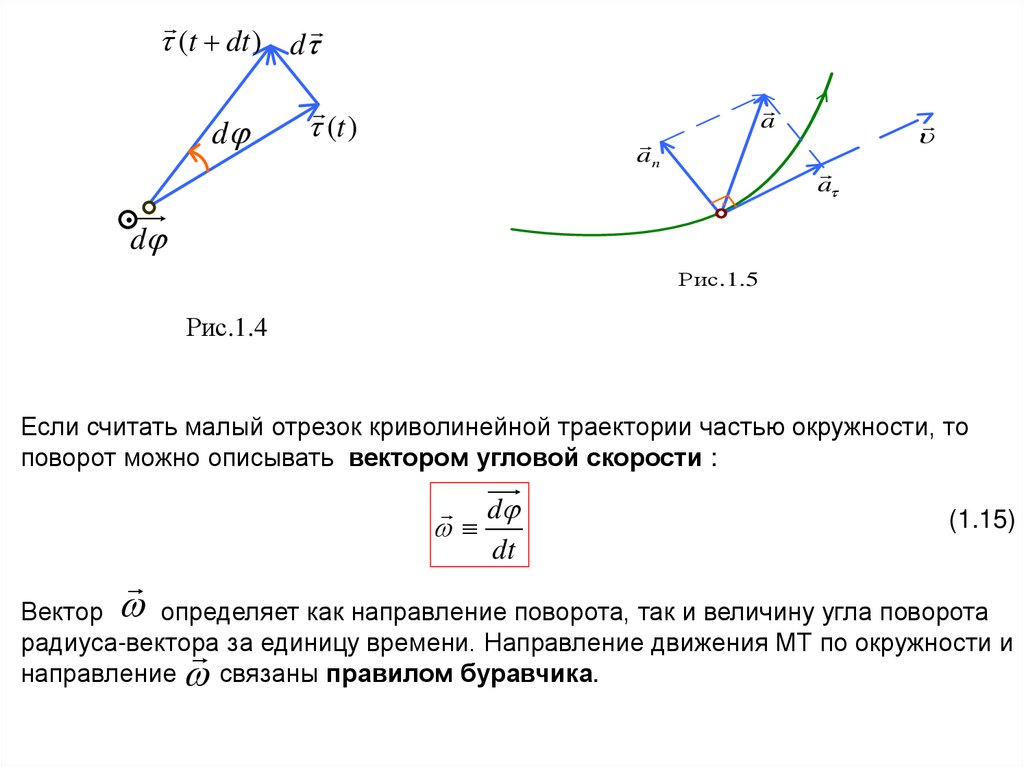
Рис.1.5
Рис.1.4
Если считать малый отрезок криволинейной траектории частью окружности, то
поворот можно описывать вектором угловой скорости :
d
dt
(1.15)
Вектор определяет как направление поворота, так и величину угла поворота
радиуса-вектора
за единицу времени. Направление движения МТ по окружности и
направление связаны правилом буравчика.

10. 1.3 УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ. СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ.

r (t dt )
O
.
d
d
r (t )
dr
Рис.1.6
Рассмотрим окружность радиуса r , по которой движется материальная
точка, т.е.
(рис.1.6).
r (t )
(t ) const
PS.
. При движении против часовой стрелки
направлена «к нам», по часовой – «от нас».

11.

Используем связь между линейной и угловой скоростями:
.
, r
(1.16)
Дифференцируя (1.16), находим полное ускорение:
d
a
, r ,
dt
a
a
a
и в соответствии с (1.14):
n
второе слагаемое есть нормальное ускорение:
, a n .
(1.17)
а первое – тангенциальное ускорение :
(1.18)
d .
a
,r
dt
Введём новое определение:
угловым ускорением МТ назовём величину
d
dt
(1.19)
Таким образом, в соотв. с (1.14)
a , r
a n 2 r

12.

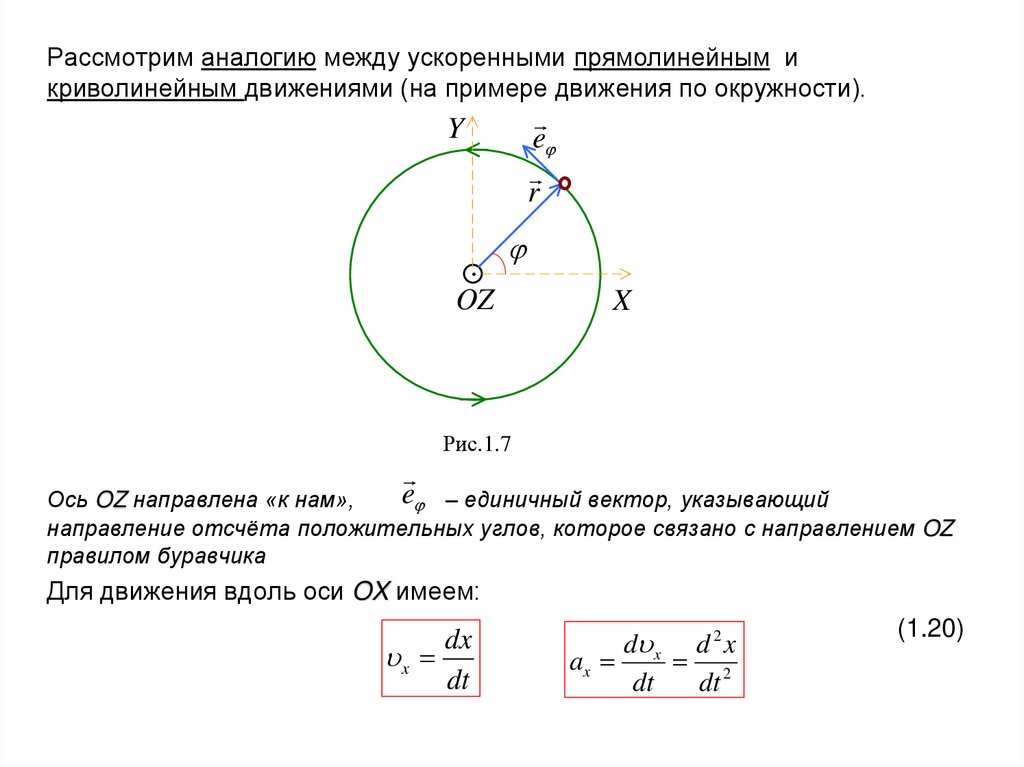
Рассмотрим аналогию между ускоренными прямолинейным и
криволинейным движениями (на примере движения по окружности).
e
r
Y
.
OZ
X
Рис.1.7
e
Ось OZ направлена «к нам»,
– единичный вектор, указывающий
направление отсчёта положительных углов, которое связано с направлением OZ
правилом буравчика
Для движения вдоль оси OX имеем:
dx
x
dt
d x d 2 x
ax
2
dt
dt
(1.20)

13.

Для движения по окружности:
z
d
dt
d z d 2
z
2
dt
dt
Обобщим, равнопеременное движение вдоль оси :
ax const
x 0 x axt
axt 2
x x0 0 xt
2
axt 2
x 0 xt
2
равнопеременное движение по окружности:
z const
z 0 z zt
0 0 zt
zt 2
2
0 z t
zt 2
2
где – угловое перемещение материальной точки:
(1.21)

14.

Таблица соответствия линейных и угловых величин
линейные
dr
a
x
x
ax
угловые
d
z
z
Уравнения, связывающие линейные и угловые переменные,
характеризующие движение МТ по окружности ( r R) :
a , r
, r
R
a R
a n 2 r
an R
2
2
R
Малую окрестность точки плоской криволинейной траектории
материальной точки можно рассматривать как малую дугу некоторой
окружности. Радиус этой окружности – радиус кривизны траектории
в окрестности данной точки, Rкр . Эта величина удовлетворяет
равенству аналогичному (1.59 б).
an
2
R.кр
(1.22)

15.

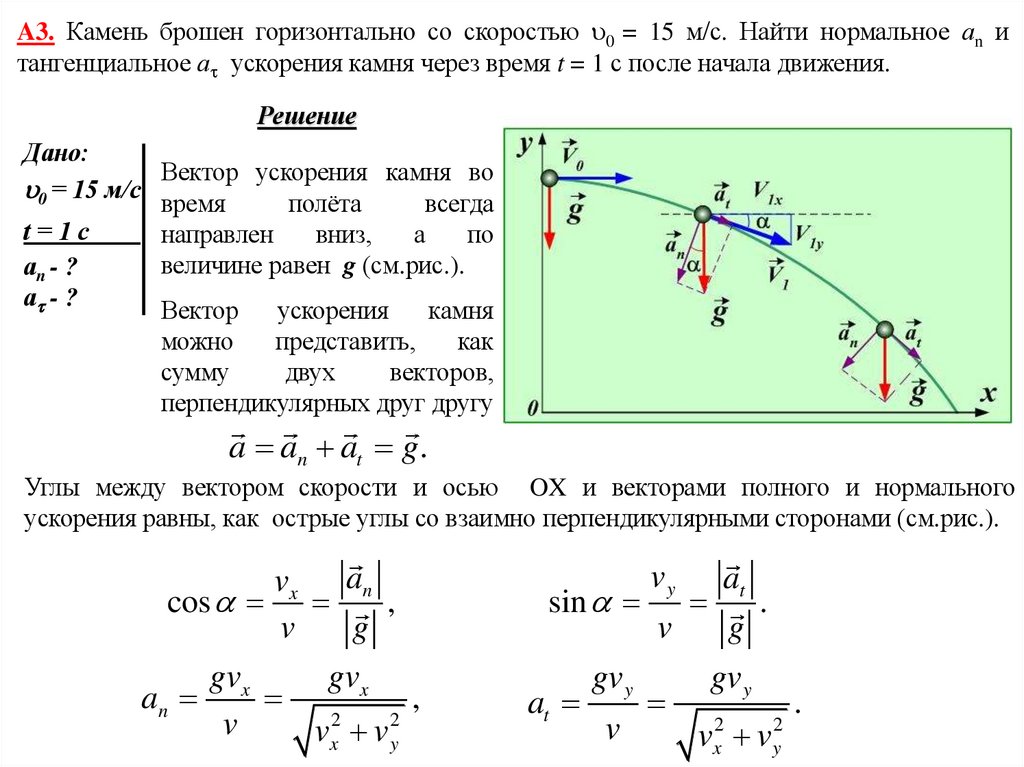
A3. Камень брошен горизонтально со скоростью 0 = 15 м/с. Найти нормальное аn и
тангенциальное а ускорения камня через время t = 1 с после начала движения.
Решение
Дано:
Вектор ускорения камня во
0 = 15 м/с время
полёта
всегда
t=1с
направлен
вниз,
а
по
величине равен g (см.рис.).
аn - ?
а - ?
Вектор
ускорения
камня
можно
представить,
как
сумму
двух
векторов,
перпендикулярных друг другу
a an at g.
Углы между вектором скорости и осью OX и векторами полного и нормального
ускорения равны, как острые углы со взаимно перпендикулярными сторонами (см.рис.).
v x an
cos
,
v
g
gvx
gvx
an
,
2
2
v
vx v y
vy
at
sin
.
v
g
gv y
gv y
at
.
2
2
v
vx v y

16.

A3. Камень брошен горизонтально со скоростью 0 = 15 м/с. Найти нормальное аn и
тангенциальное аt ускорения камня через время t = 1 с после начала движения.
Решение (продолжение)
an
gvx
gvx
gv
gv y
, at y
.
2
2
2
2
v
v
vx v y
vx v y
Камень падает в поле силы тяжести и воль оси
OX движется равномерно, а вдоль оси OY – с
постоянным ускорением g. Проекции скорости
камня зависят от времени так (см. решение
предыдущей задачи):
vx (t ) v0 ,
v y (t ) gt.
Подставим выражения для модулей проекций скорости в формулы для an и at:
an
an
gv0
v02 g 2t 2
g 2t
v02 g 2t 2
9,8 15
152 9,82 12
9,82 1
152 9,82 12
8, 2( м / с 2 ),
5, 4( м / с 2 ).
Ответ: an = 8,2 м/c2; at = 5,4 м/с2.

17.

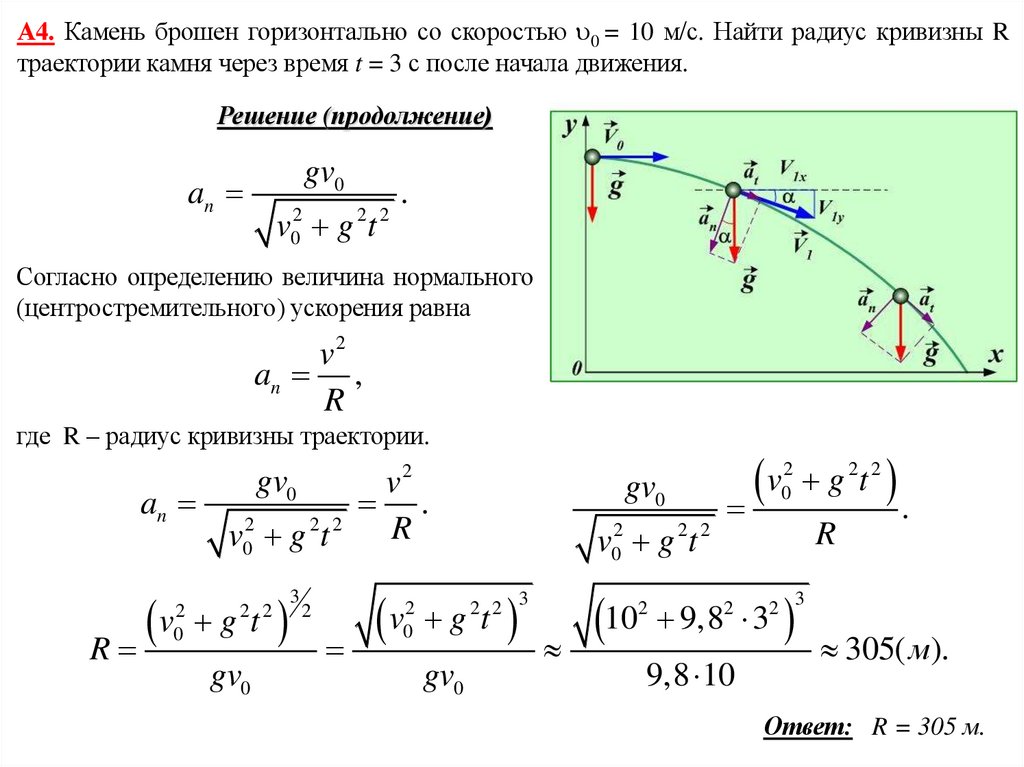
А4. Камень брошен горизонтально со скоростью 0 = 10 м/с. Найти радиус кривизны R
траектории камня через время t = 3 с после начала движения.
Решение
Дано:
Вектор ускорения камня во
полёта
всегда
0 = 10 м/с время
направлен
вниз,
а
по
t=3с
величине равен g (см.рис.).
R- ?
Вектор
ускорения
камня
можно
представить,
как
сумму
двух
векторов,
перпендикулярных друг другу
a an at g.
Углы между вектором скорости и осью OX и векторами полного и нормального
ускорения равны, как острые углы со взаимно перпендикулярными сторонами (см.рис.).
v x an
cos
,
v
g
an
gvx
gvx
gv0
.
2
2
2
2
2
v
vx v y
v0 g t

18.

А4. Камень брошен горизонтально со скоростью 0 = 10 м/с. Найти радиус кривизны R
траектории камня через время t = 3 с после начала движения.
Решение (продолжение)
gv0
an
v g t
2
0
2 2
.
Согласно определению величина нормального
(центростремительного) ускорения равна
v2
an ,
R
где R – радиус кривизны траектории.
v2
an
.
2
2 2
R
v0 g t
gv0
v g t
R
2
0
2 2
gv0
3
2
gv0
v02 g 2t 2
v g t
2 2 3
2
0
gv0
2
0
2 2
R
10 9,8 3
2
v g t
.
2
9,8 10
2 3
305( м).
Ответ: R = 305 м.

19.

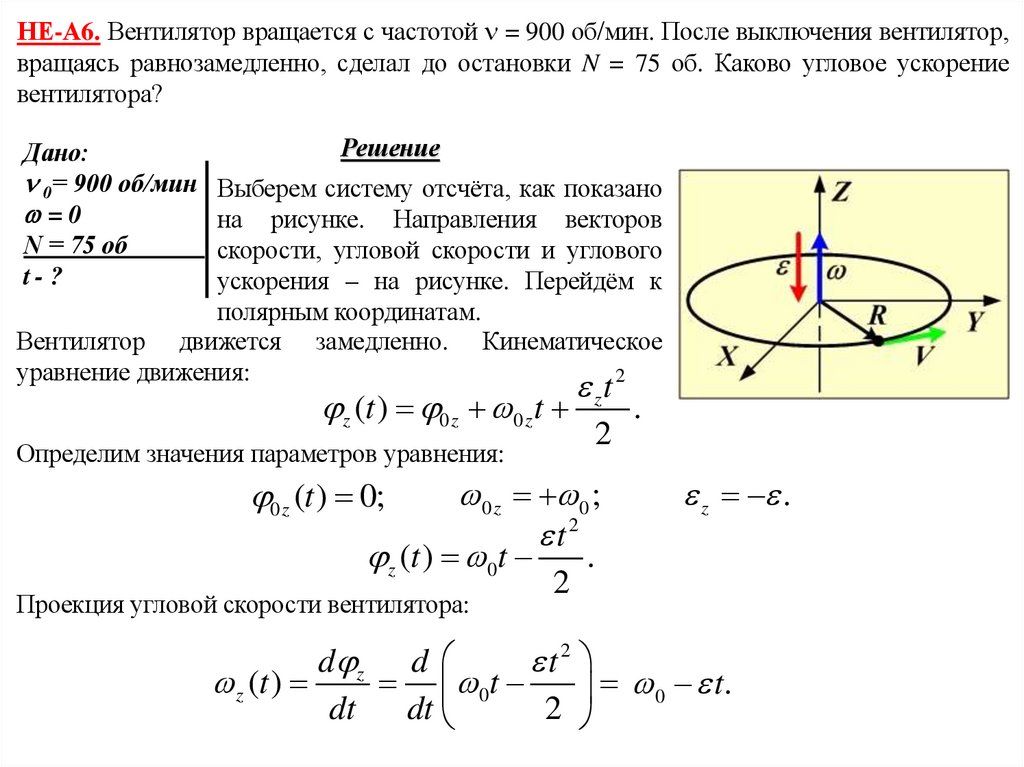
НЕ-А6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор,
вращаясь равнозамедленно, сделал до остановки N = 75 об. Каково угловое ускорение
вентилятора?
Дано:
0= 900 об/мин
=0
N = 75 об
t- ?
Решение
Выберем систему отсчёта, как показано
на рисунке. Направления векторов
скорости, угловой скорости и углового
ускорения – на рисунке. Перейдём к
полярным координатам.
Вентилятор движется замедленно. Кинематическое
уравнение движения:
2
z (t ) 0 z 0 z t
Определим значения параметров уравнения:
zt
2
0 z 0 ;
t2
z (t ) 0t
.
2
0 z (t ) 0;
.
z .
Проекция угловой скорости вентилятора:
d z d
t2
z (t )
0t
0 t.
dt
dt
2

20.

неА6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор,
вращаясь равнозамедленно, сделал до остановки N = 75 об. Каково угловое ускорение
вентилятора?
Решение (продолжение)
Уравнения движения в полярных координатах:
z (t ) 0t
t2
2
z (t ) 0 t.
.
Из второго уравнения выразим t :
0 z (t )
t
. Когда вентилятор остановится, z (t ) 0.
0
t .
2
2
2
t
z (t ) 0t
0 0 0 0 .
2
2 2
0 2 0 .
Когда вентилятор остановится, проекция углового перемещения составит
z 2 N .

21.

English Русский Rules