Решение систем двух линейных уравнений с двумя переменными

1.

Решение систем двух
линейных уравнений с двумя
переменными

2.

3.

Алгоритм решения системы уравнений графическим
способом
1. Приводим оба уравнения к виду линейной функции
y = k x + m.
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной
плоскости.
4. Определяем число решений:
• Если прямые пересекаются, то одно решение пара
чисел (х ; у) – координаты точки пересечения;
• Если прямые параллельны, то нет решений;
• Если прямые совпадают, то бесконечно много
решений.
5. Записываем ответ.

4.

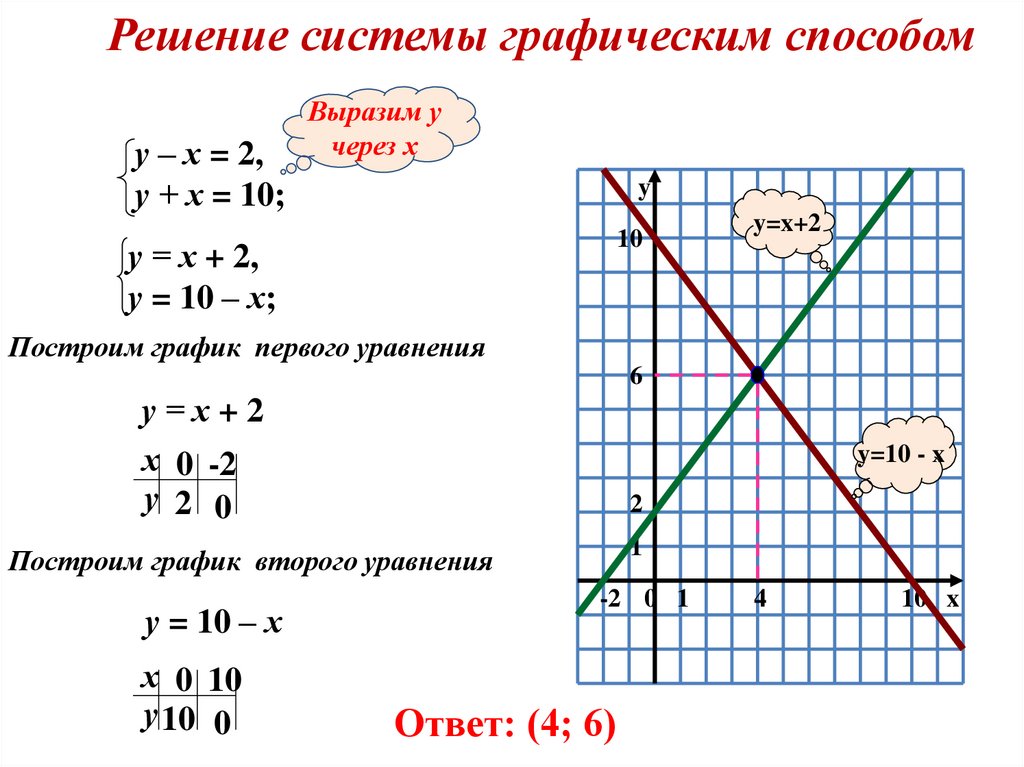
Решение системы графическим способом
у – х = 2,
у + х = 10;
Выразим у
через х
y
10
у = х + 2,
у = 10 – х;
y=x+2
Построим график первого уравнения
6
у=х+2
х 0 -2
у 2 0
y=10 - x
2
1
Построим график второго уравнения
у = 10 – х
х 0 10
у 10 0
-2 0 1
Ответ: (4; 6)
4
10 x

5.

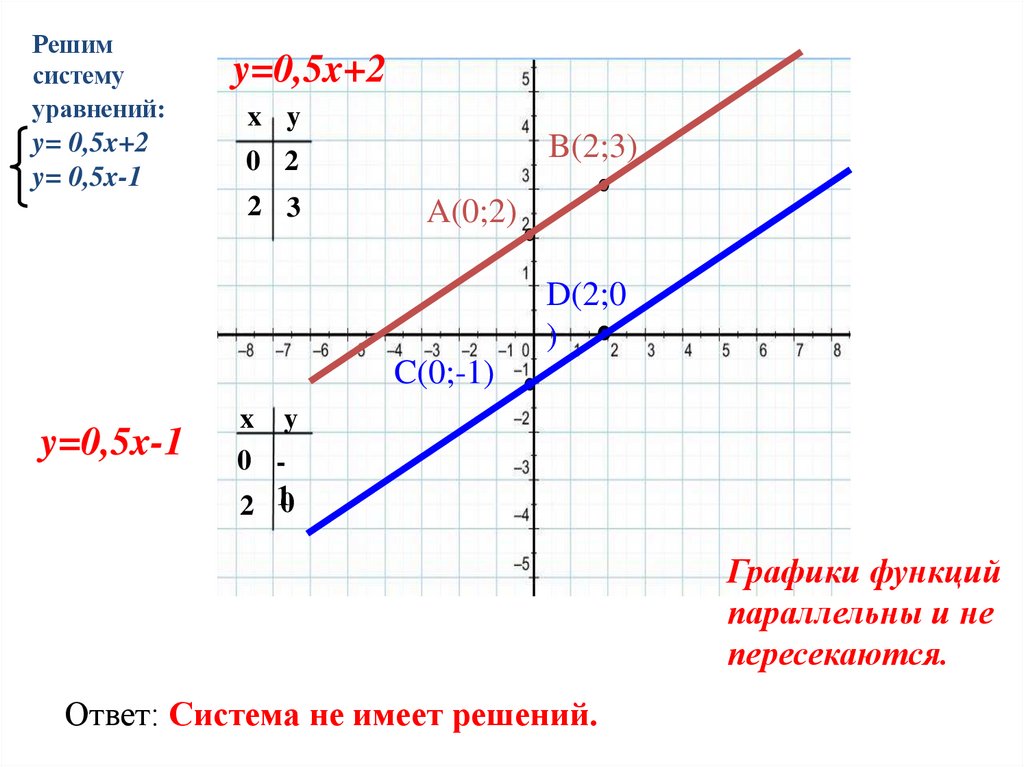
Решим
систему
уравнений:
y=0,5x+2
y= 0,5x+2
y= 0,5x-1
0 2
x y
2 3
B(2;3)
A(0;2)
D(2;0
)
C(0;-1)
y=0,5x-1
x y
0 2 10
Графики функций
параллельны и не
пересекаются.
Ответ: Система не имеет решений.

6.

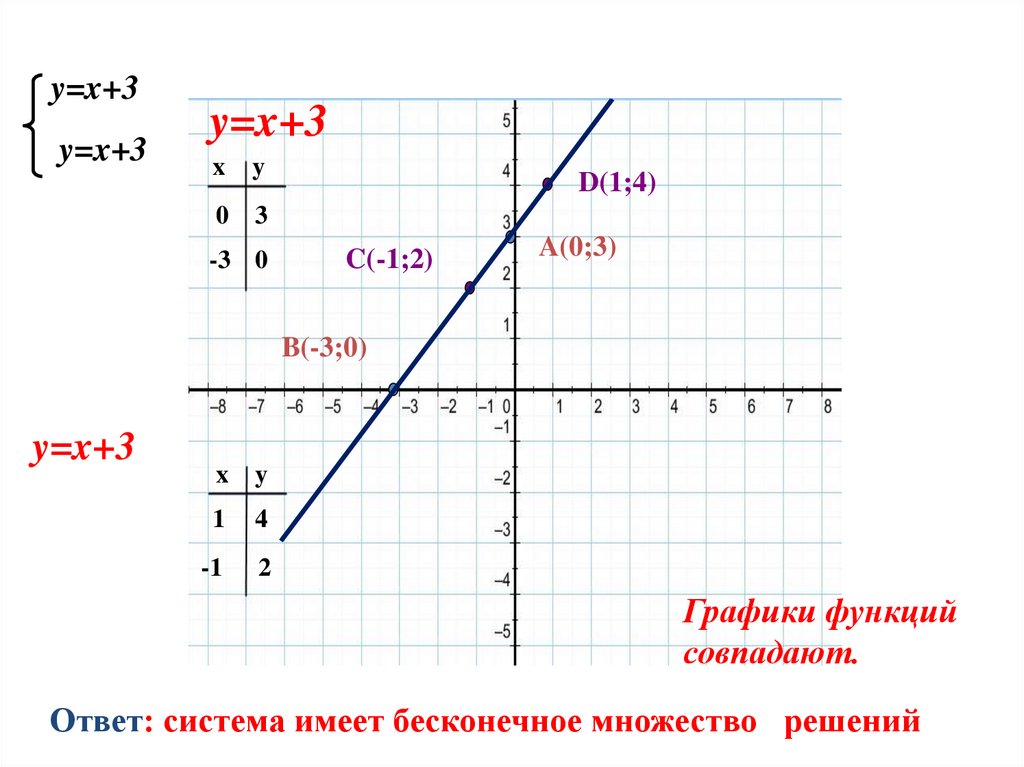
y=x+3
y=x+3
y=x+3
x
y
0
3
-3 0
D(1;4)
C(-1;2)
A(0;3)
B(-3;0)
y=x+3
x
y
1
4
-1
2
Графики функций
совпадают.
Ответ: система имеет бесконечное множество решений

7.

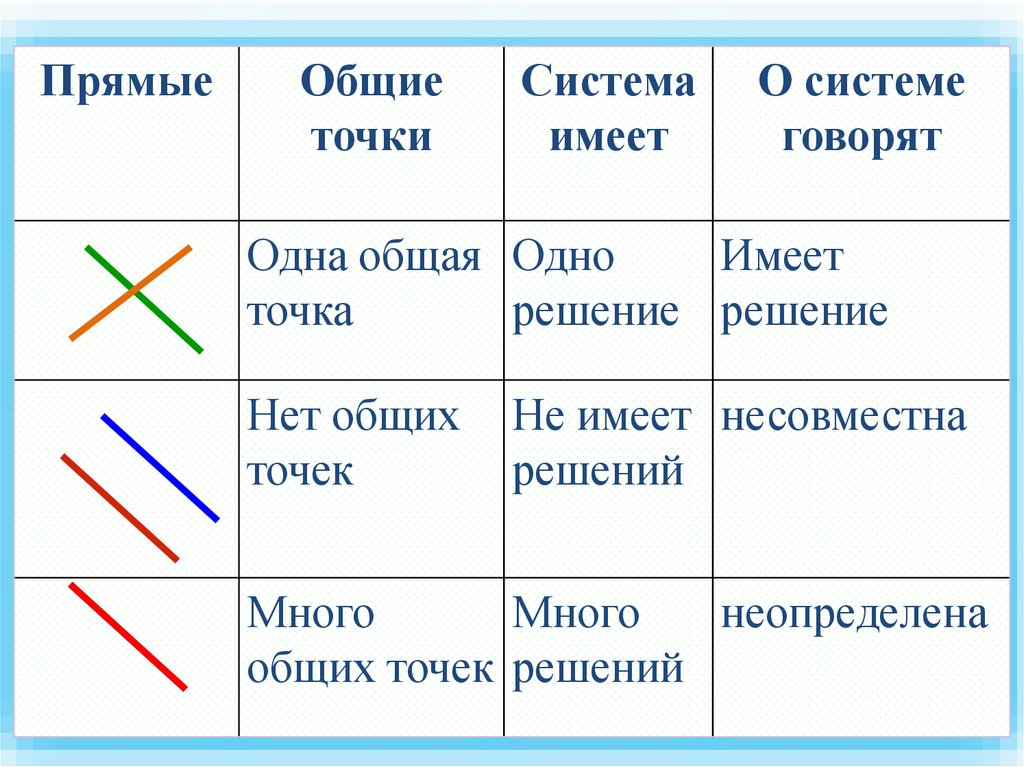
Прямые
Общие
точки
Система
имеет
О системе
говорят
Одна общая Одно
Имеет
точка
решение решение
Нет общих
точек
Не имеет несовместна
решений
Много
Много
неопределена
общих точек решений

8.

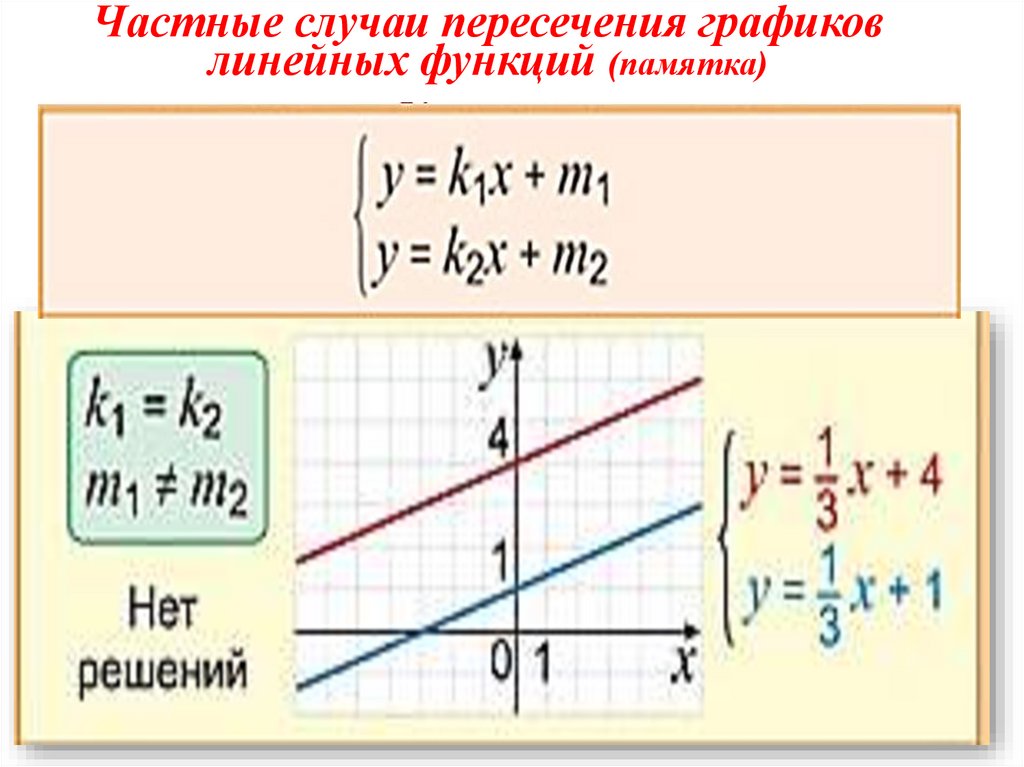
Частные случаи пересечения графиков
линейных функций (памятка)

9.

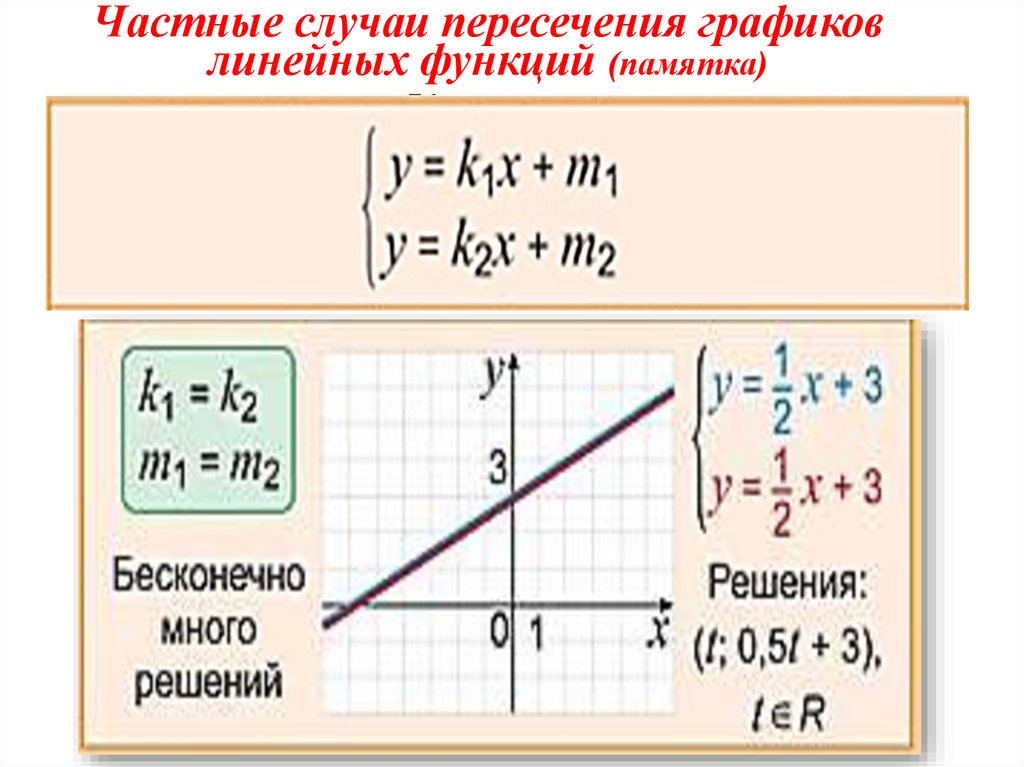
Частные случаи пересечения графиков
линейных функций (памятка)

10.

Частные случаи пересечения графиков
линейных функций (памятка)

11.

Алгоритм решения системы двух уравнений с двумя
переменными способом подстановки
1) Из одного уравнения системы выразить одну
переменную через другую (у через х или х через у)
2) Полученное выражение подставить в другое
уравнение системы. Получится уравнение с одной
переменной (либо с переменной х, либо с переменной
у)
3) Решить это уравнение. Найти соответственно х,
либо у.
4) Подставить найденное значение х или у в
выражение для у или х. И найти значение у или х.
5) Записать ответ в виде пары значений (х; у).

12.

Решение системы
методом подстановки
у - 2х=4
7х - у =1
у=2х+4
7х - у=1
у=2х+4
7х - (2х+4)=1
7х - 2х - 4 = 1
5х = 5
х=1
у=2х+4
х=1
у=6
х=1
Ответ: х=1; у=6.

13.

Алгоритм решения линейных систем уравнений с двумя
переменными методом алгебраического сложения
1) Рассмотреть коэффициенты при переменных х и у. При
необходимости умножить уравнения системы, подбирая
множители так, чтобы коэффициенты при одной из
переменных уравнялись (стали либо одинаковыми, либо
противоположными).
2) Если коэффициенты при одной из переменной (х или у)
одинаковы, то необходимо из первого уравнения вычесть
второе.
3) Если коэффициенты при одной из переменной (х или у)
отличаются только знаком, то необходимо почленно
сложить данные уравнения.
4) Решить получившееся уравнение относительно одной
переменной (х или у).
5) Найти соответствующее значение второй переменной.
6)Записать ответ.

14.

2х + 3у = -5
х - 3у = 38
Решение
2х + 3у = -5
х - 3у = 38
2х +3у + х - 3у = -5 + 38
3х = 33
х =33 : 3
х = 11
Ответ: (11; -9)
2·11 + 3у = -5
22 +3у = -5
3у = -5 -22
3у = -27
у = -27 : 3
у = -9

15.

7х+2у=1
17х+6у=-9
Решение
7х+2у=1 | · (-3)
17х+6у=-9
-21х - 6у= -3,
17х + 6у= -9.
7·3+2у=1
21+2у=1
2у=1 - 21
2у=-20
у = -20:2
у = -10
-21x-6y+17x+6y=-3+(-9)
-4x=-12
x=3
Ответ: (3; - 10)

16.

5х -4у = 10
2х -3у = -3
5х -4у = 10 | ·2
2х -3у = -3 | · (-5)
10х - 8у = 20
–10х +15у = 15
10x-8y-10x+15y=20+15
2х - 3·5 = -3
2х - 15 = -3
2х = -3+15
2х=12
х =12 : 2
х=6
7y=35
y=5
Ответ: (6; 5)