Монотонность функции. Точки экстремума функции

1. Цели занятия:

Учебные цели: определять по графику
свойства
функции
(нули,
промежутки
знакопостоянства, промежутки монотонности,
наибольшие и наименьшие значения и т.п.);
строить
эскиз
графика
функции,
удовлетворяющей
приведенному
набору
условий (промежутки возрастания/убывания,
значение функции в заданной точке, точки
экстремумов и т.д.).

2.

Устная работа
Повторите возрастание и убывание функции
Функция y = f(x) возрастает на промежутке, если для
любых значений аргумента х и х из этого промежутка,
таких что х > х выполняется соотношение f(х )> f(х )
1
2
1
2
2
1

3.

Устная работа
Рассмотрите примеры графиков возрастающих
функций

4.

Устная работа
Повторите возрастание и убывание функции
Функция y = f(x) убывает на промежутке, если для
любых значений аргумента х и х из этого промежутка,
таких что х > х выполняется соотношение f(х )< f(х )
1
2
1
2
2
1

5.

Устная работа
Примеры графиков убывающих функций

6. Устная работа Рассмотрите график функции и ответьте на вопросы

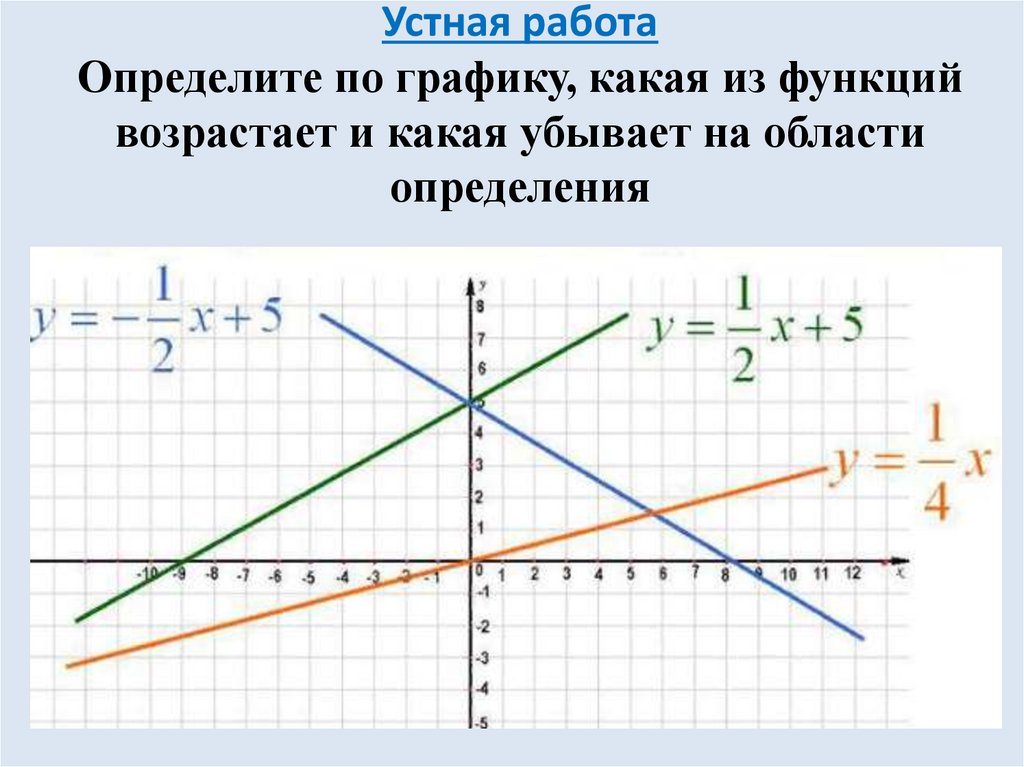
7. Устная работа Определите по графику, какая из функций возрастает и какая убывает на области определения

8. Устная работа

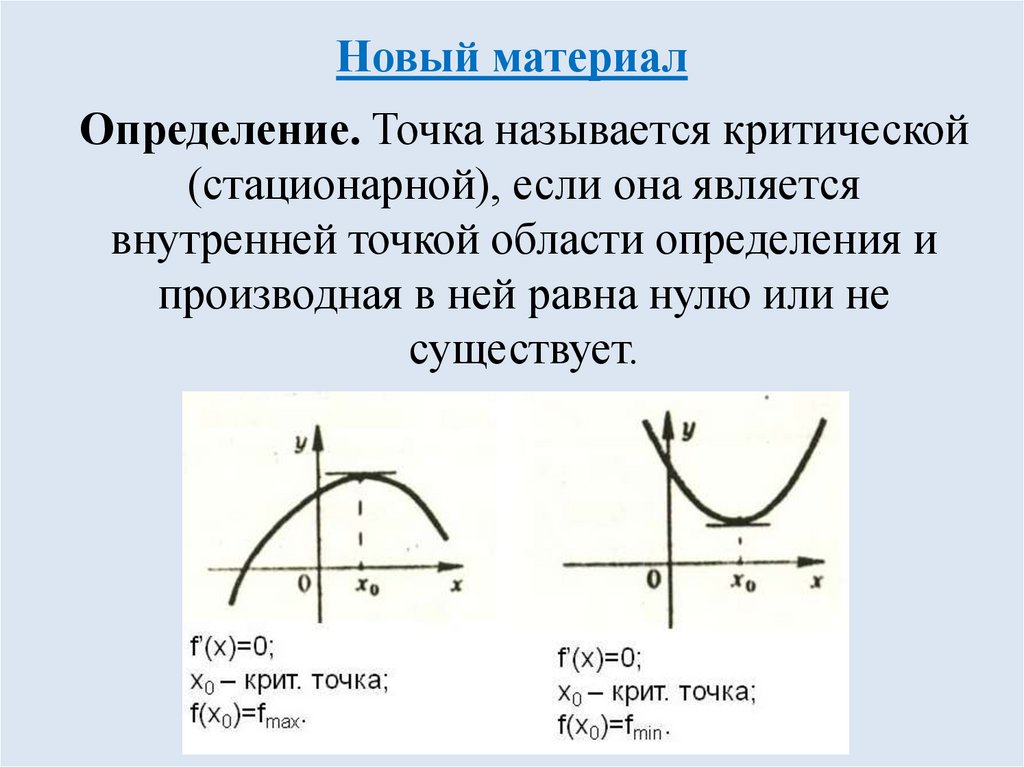
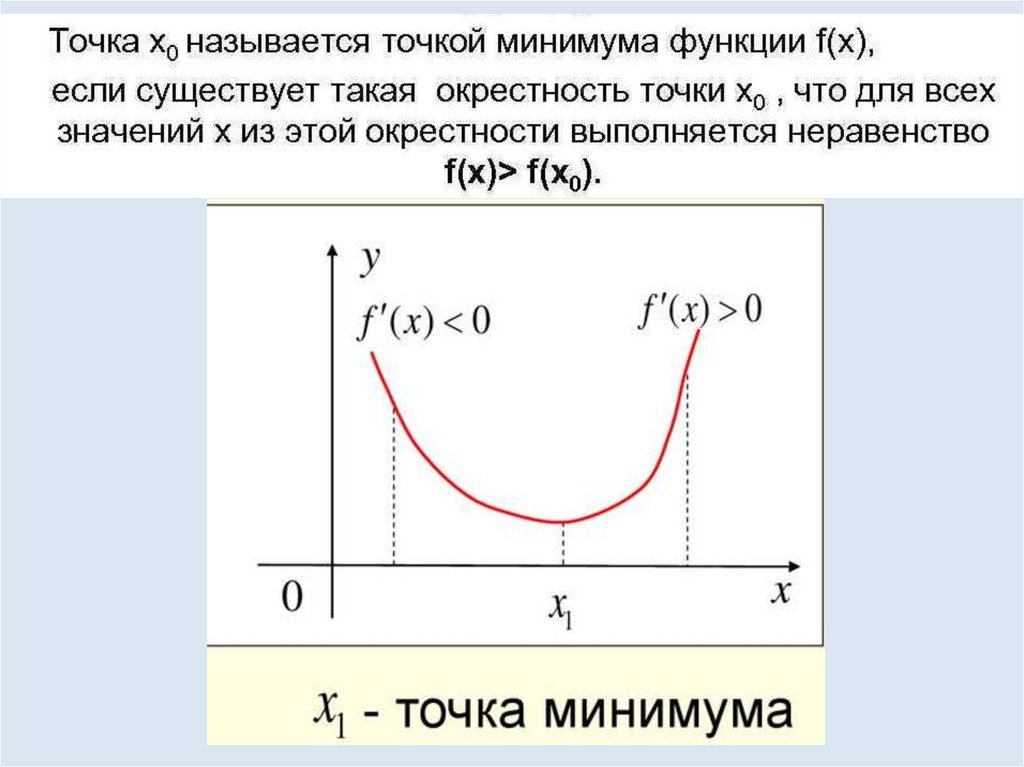
9. Новый материал

Определение. Точка называется критической
(стационарной), если она является
внутренней точкой области определения и
производная в ней равна нулю или не
существует.

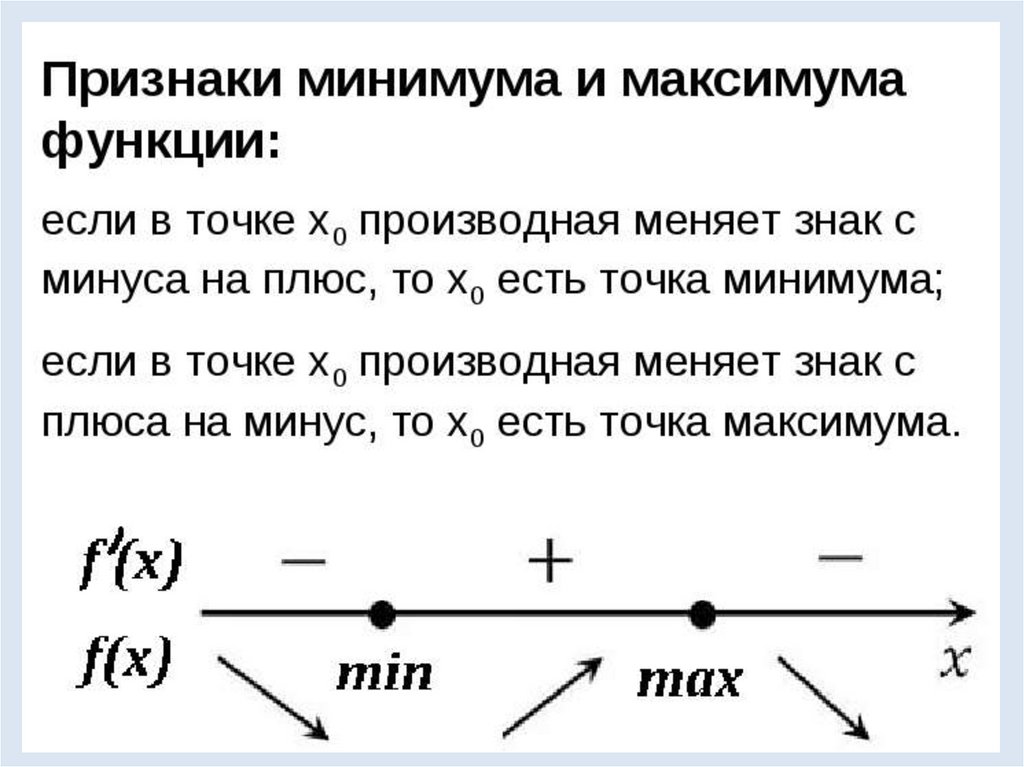
10.

Достаточный признак возрастания функции:
Если функция fʹ(x)>0 в каждой точке интервала I,
то функция возрастает на I.

11. Достаточный признак убывания функции: Если функция f(x) fʹ(x)<0 в каждой точке интервала I, то функция убывает на I.

Достаточный признак убывания функции:
Если функция f(x) fʹ(x)<0 в каждой точке
интервала I, то функция убывает на I.

12.

Промежутки возрастания и убывания функции
называют промежутками монотонности
функции

13. ё

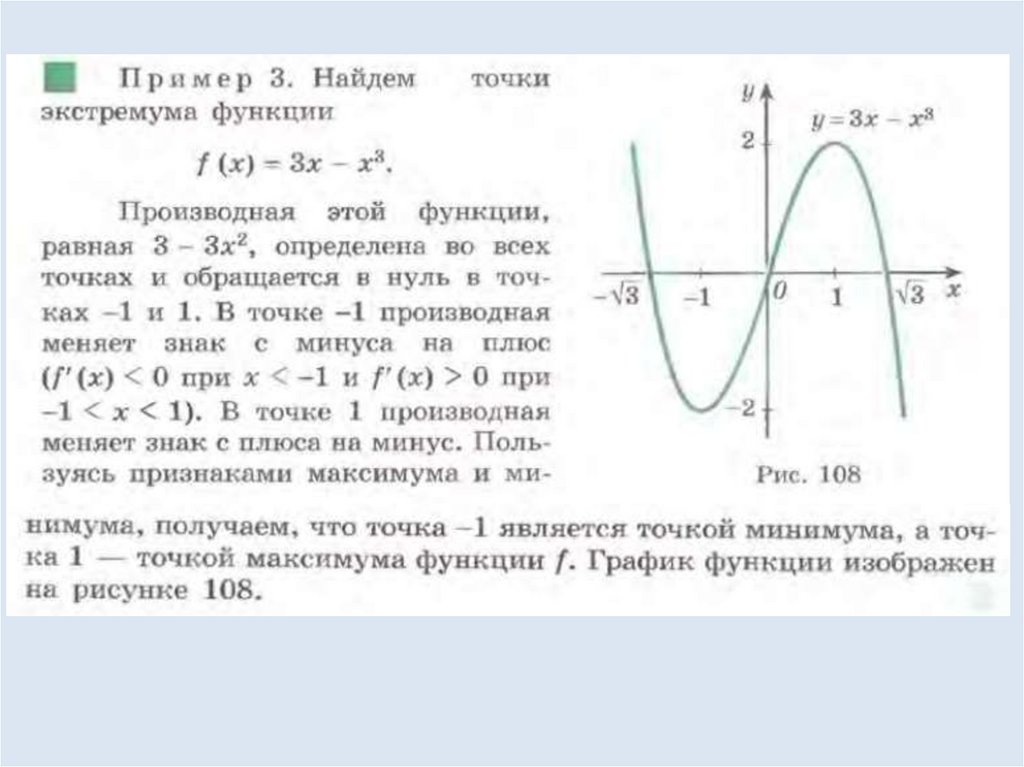
14. Рассмотрите примеры нахождение промежутков монотонности

15.

16. Задание1. Исследовать функцию на монотонность

17. Решение:

18. Задание 2.

19. Решение:

20.

21.

22.

23.

24.

25.

26. Самостоятельная работа

1. Найдите точки экстремума функции.
у=3х4-16х3+24х2-11
2. Определите промежуток монотонности
функции у=х2 -8х +5

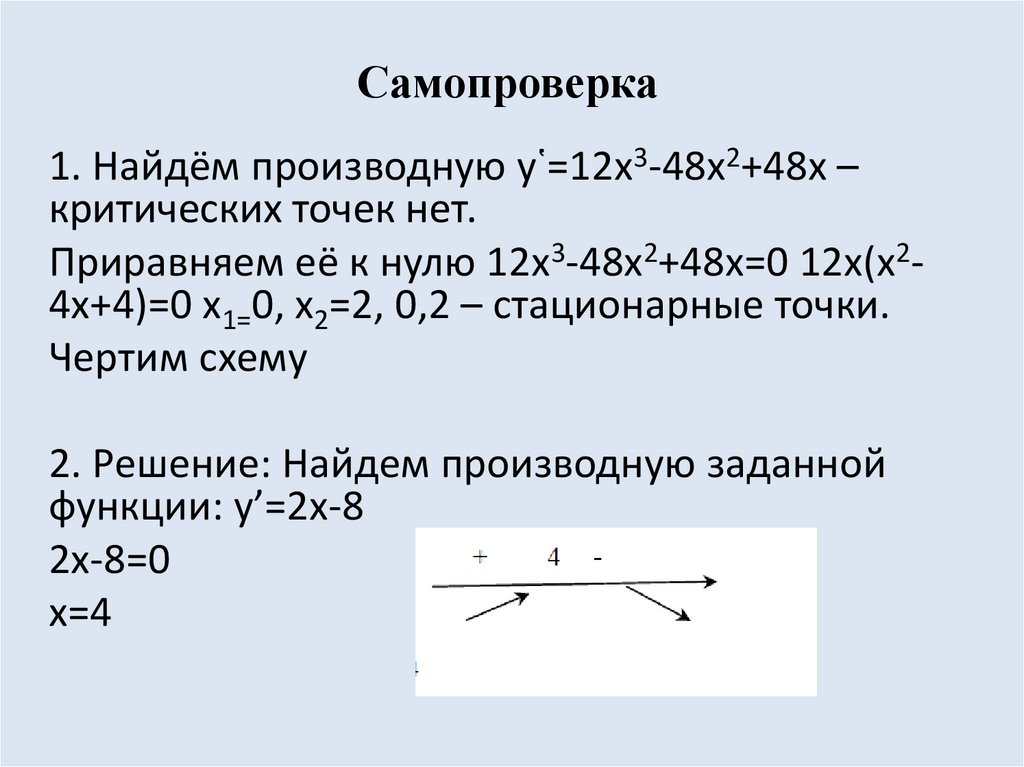
27. Самопроверка

1. Найдём производную у῾=12х3-48х2+48х –
критических точек нет.
Приравняем её к нулю 12х3-48х2+48х=0 12х(х24х+4)=0 х1=0, х2=2, 0,2 – стационарные точки.
Чертим схему
2. Решение: Найдем производную заданной
функции: у’=2x-8
2x-8=0
х=4

28. Спасибо за внимание