Монотонность функции. Точки экстремума функции

1.

«Монотонность функции.
Точки экстремума
функции»

2.

…Нет ни одной области в математике,
которая когда-либо не окажется
применимой к явлениям действительного
мира …
Н.И. Лобачевский

3. Цели занятия:

Учебные цели:
научиться
определять
критические
(стационарные) точки, признаки возрастания и
убывания функции и признаки максимума и
минимума функции, алгоритмы нахождения
промежутков монотонности и точек экстремума
функции.

4.

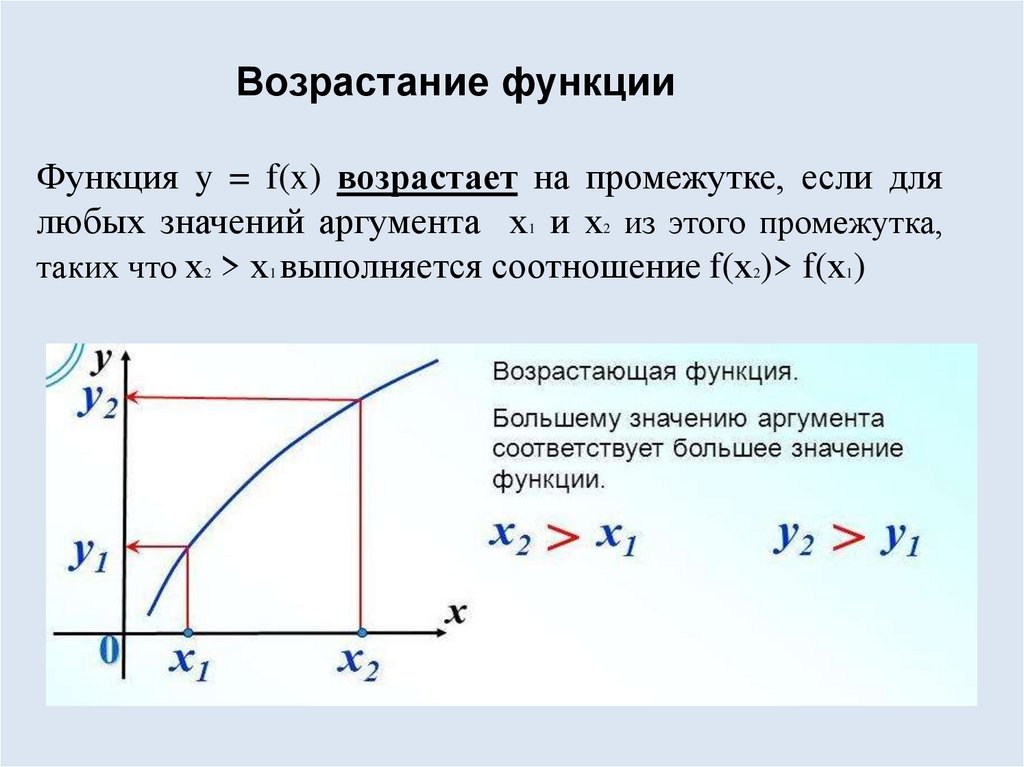
Возрастание функции
Функция y = f(x) возрастает на промежутке, если для
любых значений аргумента х и х из этого промежутка,
таких что х > х выполняется соотношение f(х )> f(х )
1
2
1
2
2
1

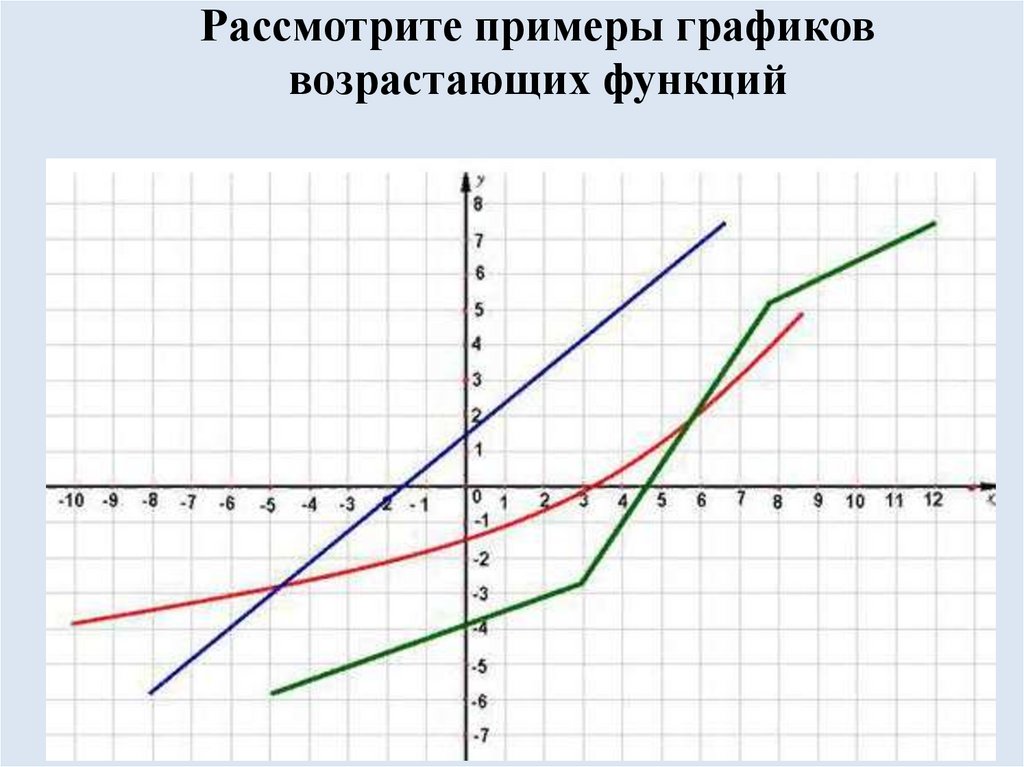
5. Рассмотрите примеры графиков возрастающих функций

6.

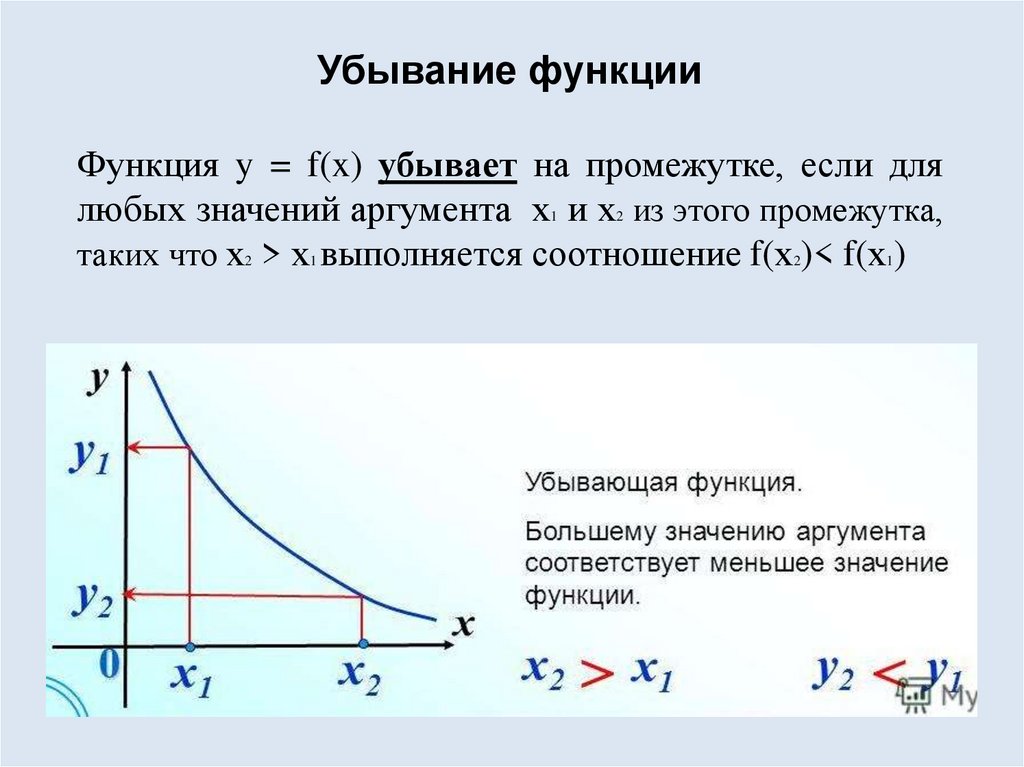
Убывание функции
Функция y = f(x) убывает на промежутке, если для
любых значений аргумента х и х из этого промежутка,
таких что х > х выполняется соотношение f(х )< f(х )
1
2
1
2
2
1

7.

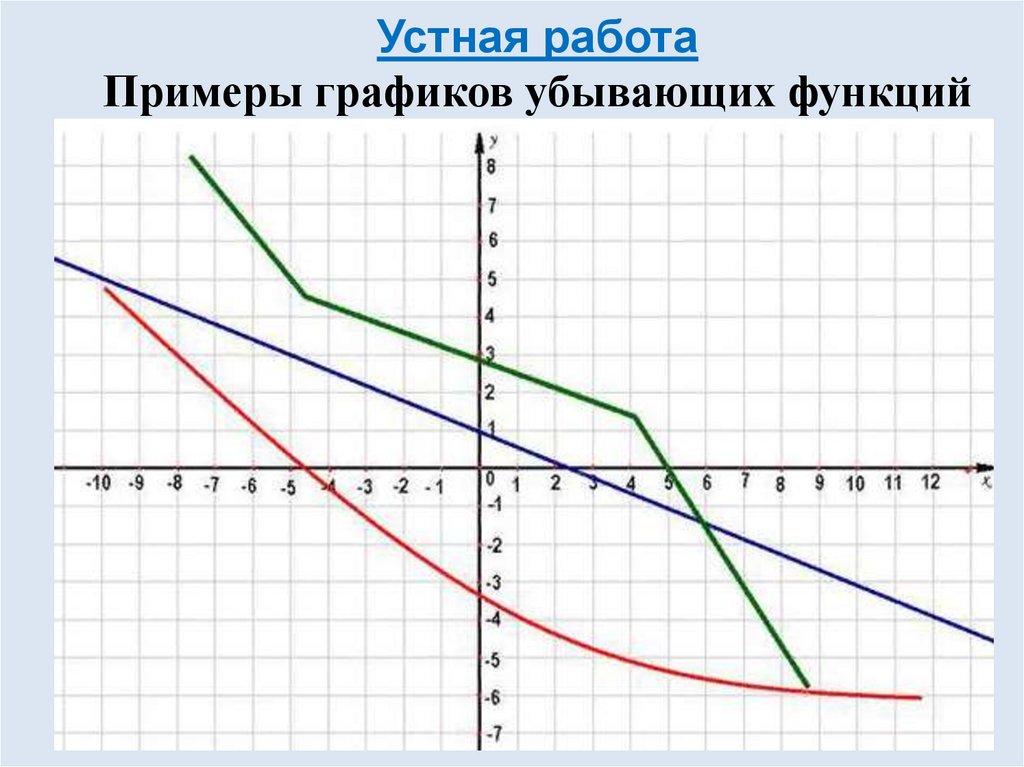
Устная работа
Примеры графиков убывающих функций

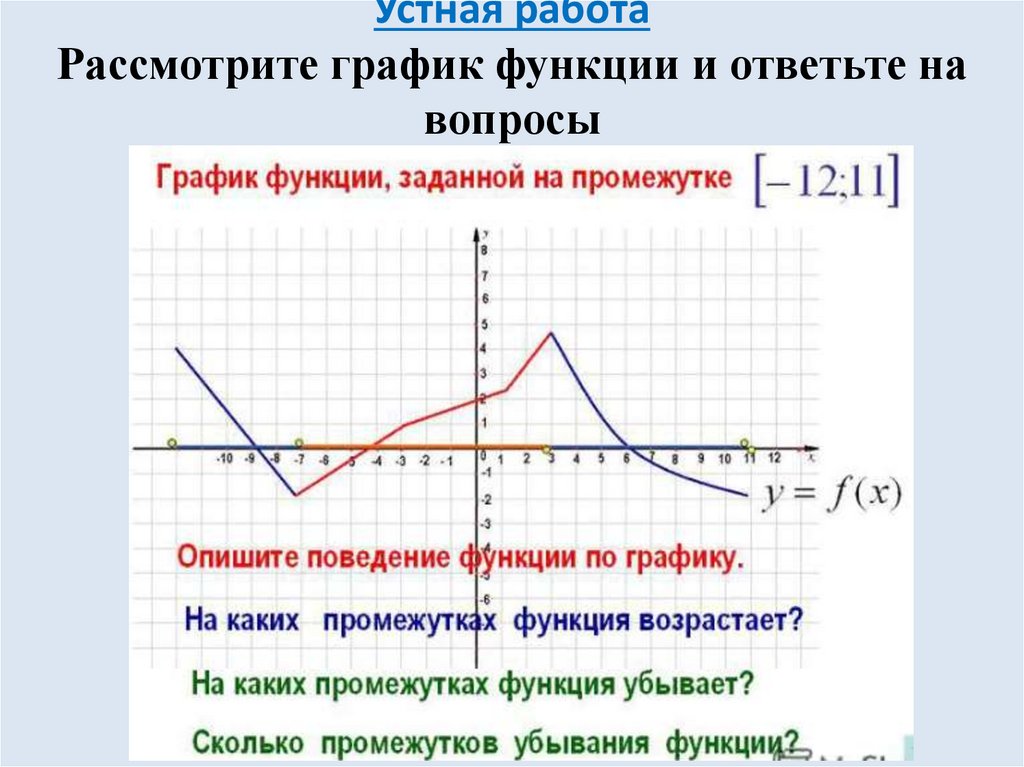
8. Устная работа Рассмотрите график функции и ответьте на вопросы

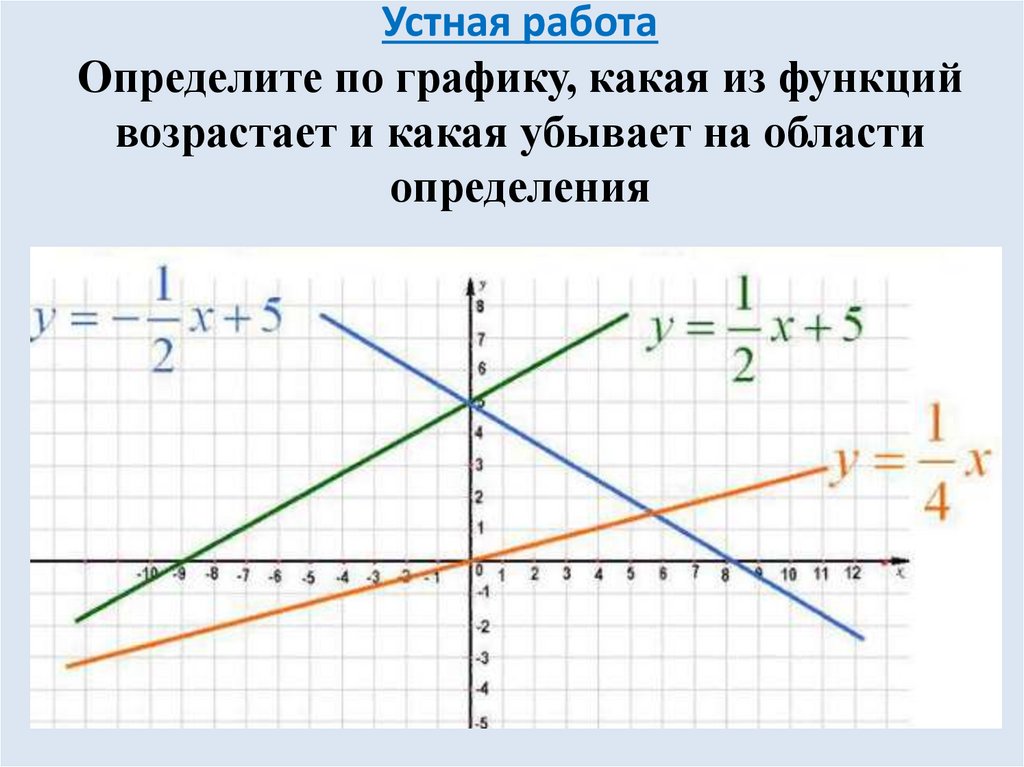
9. Устная работа Определите по графику, какая из функций возрастает и какая убывает на области определения

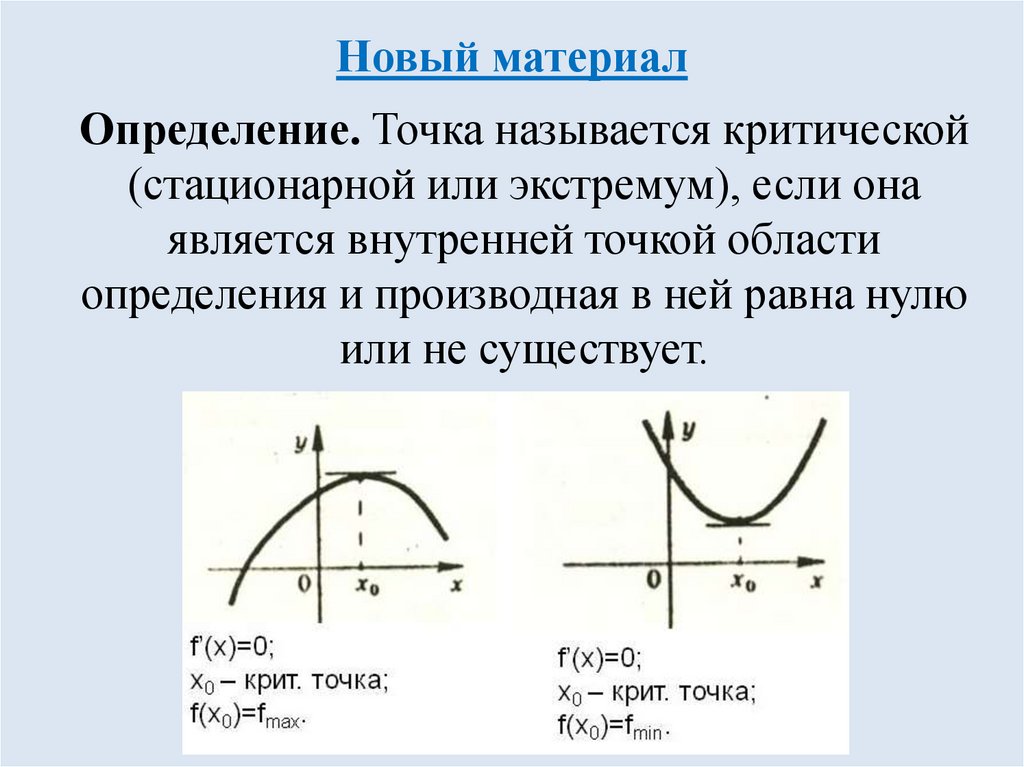
10. Новый материал

Определение. Точка называется критической
(стационарной или экстремум), если она
является внутренней точкой области
определения и производная в ней равна нулю
или не существует.

11.

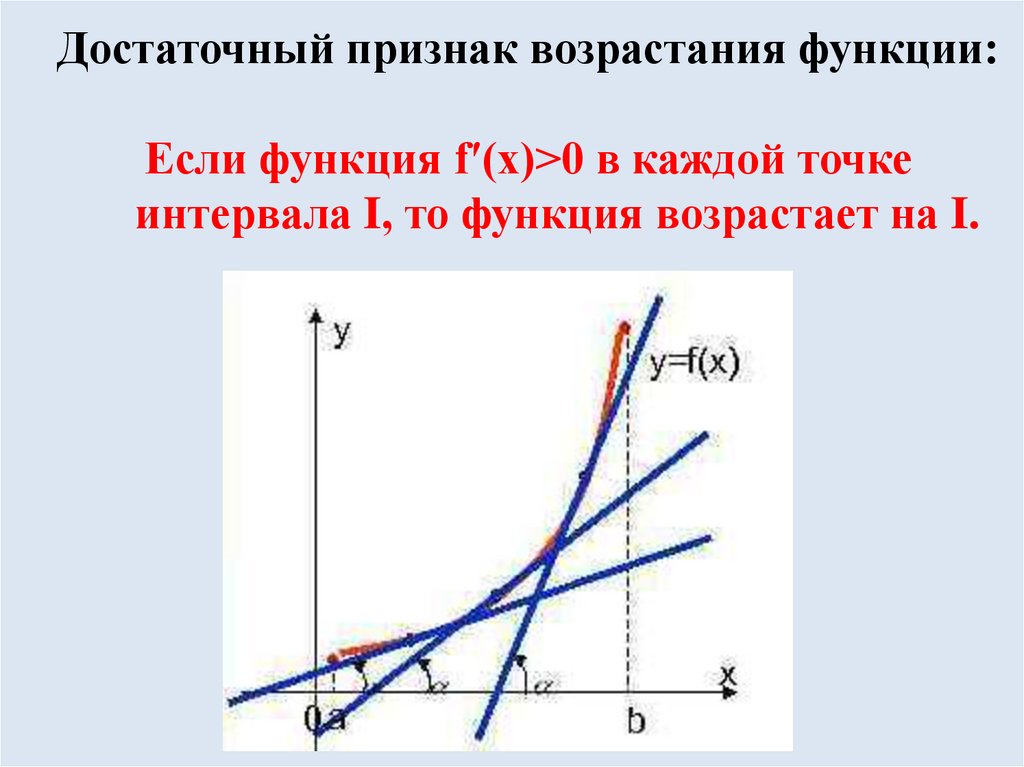
Достаточный признак возрастания функции:
Если функция fʹ(x)>0 в каждой точке
интервала I, то функция возрастает на I.

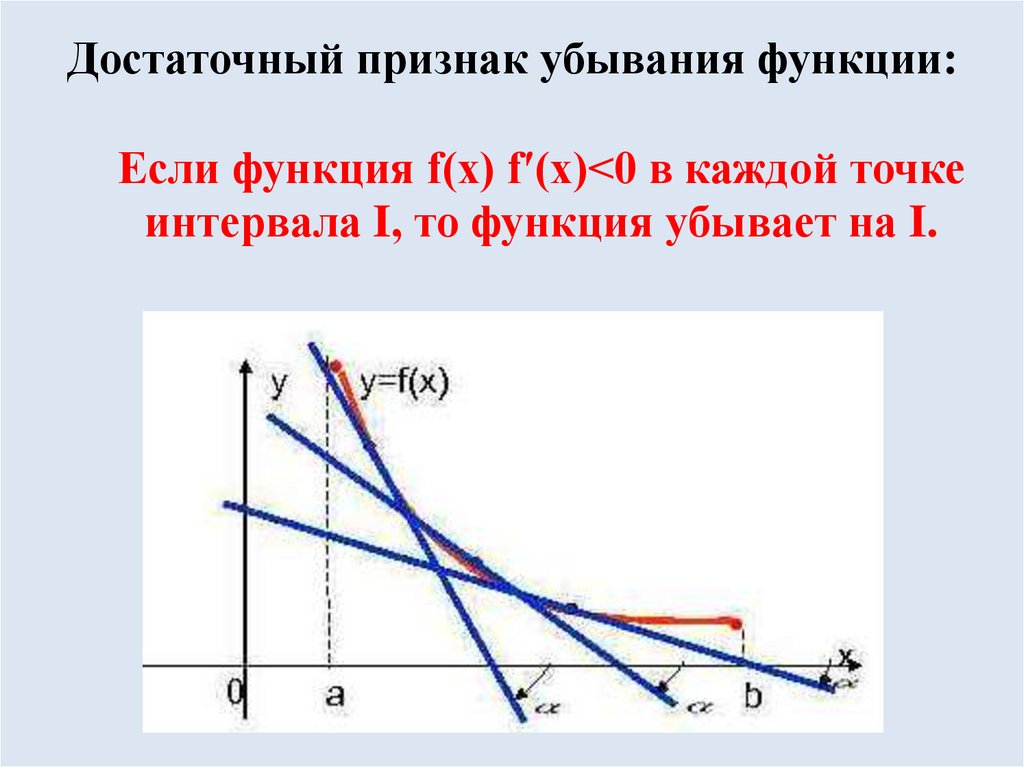
12. Достаточный признак убывания функции: Если функция f(x) fʹ(x)<0 в каждой точке интервала I, то функция убывает на I.

Достаточный признак убывания функции:
Если функция f(x) fʹ(x)<0 в каждой точке
интервала I, то функция убывает на I.

13.

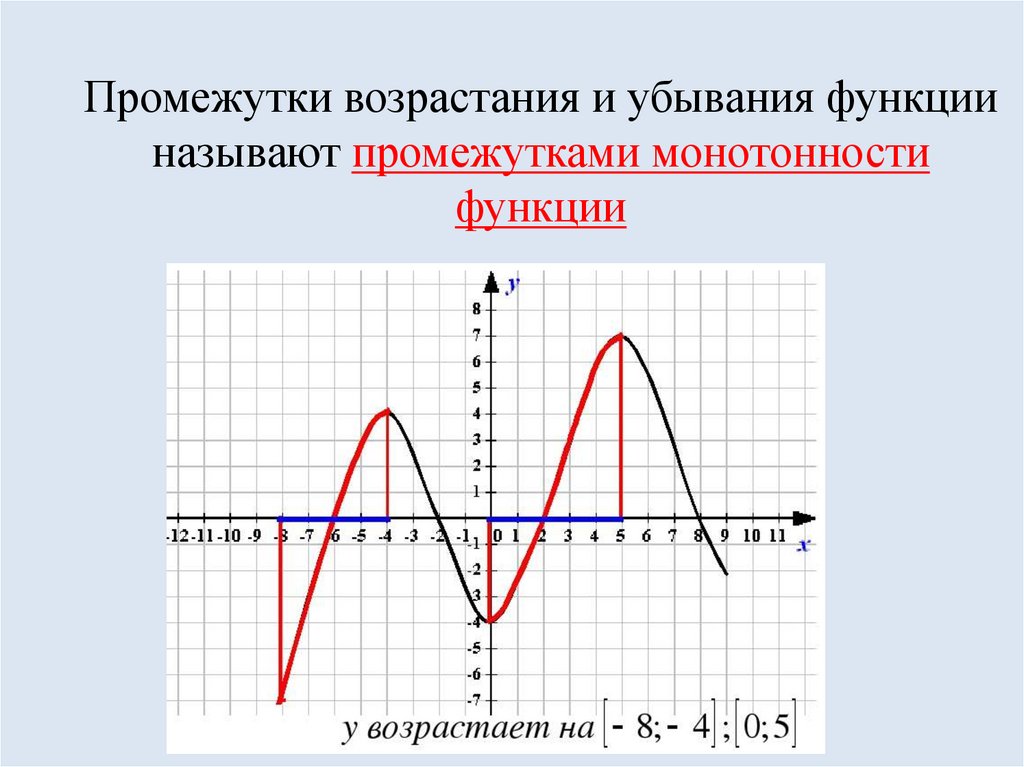
Промежутки возрастания и убывания функции
называют промежутками монотонности
функции

14.

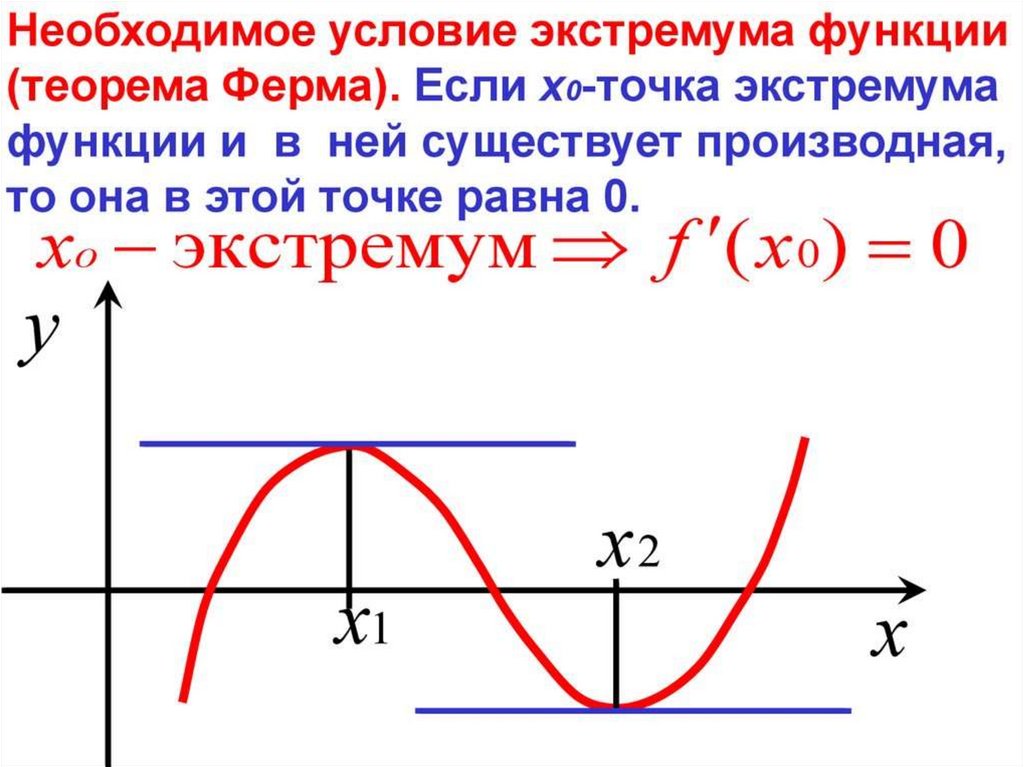
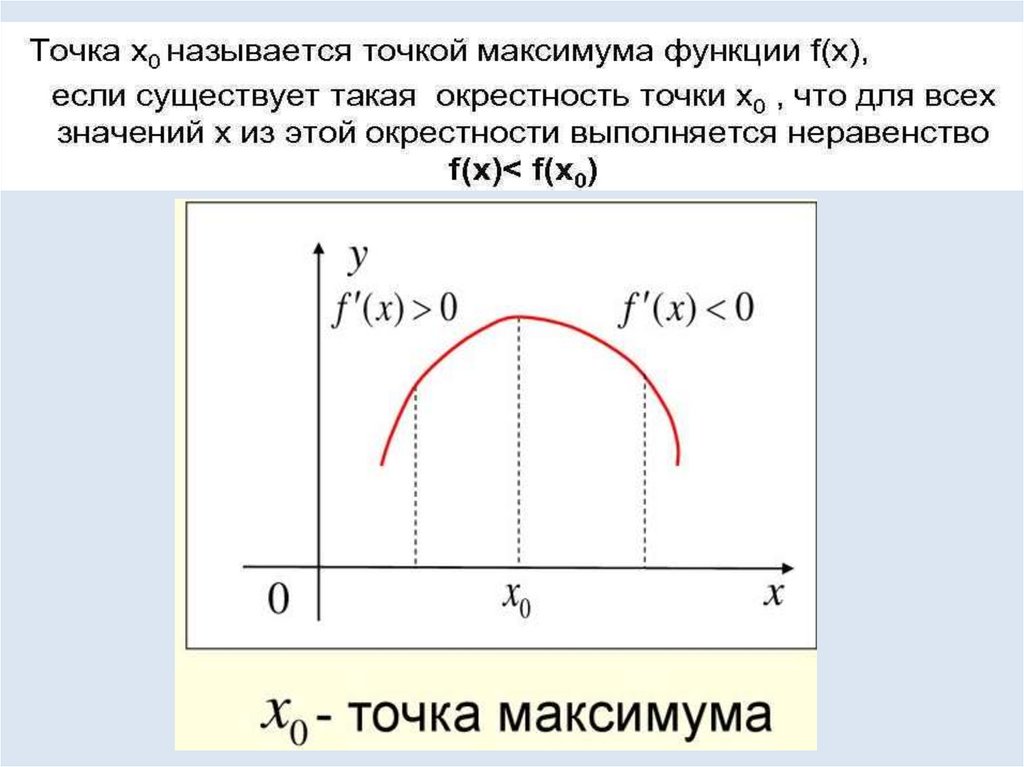
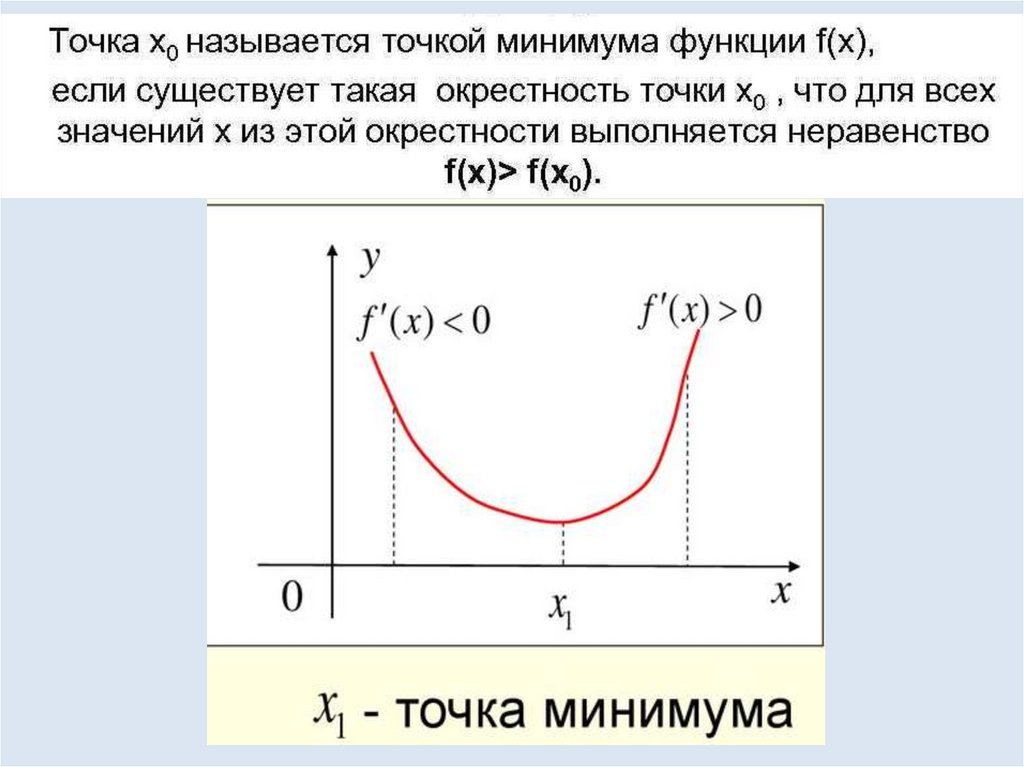
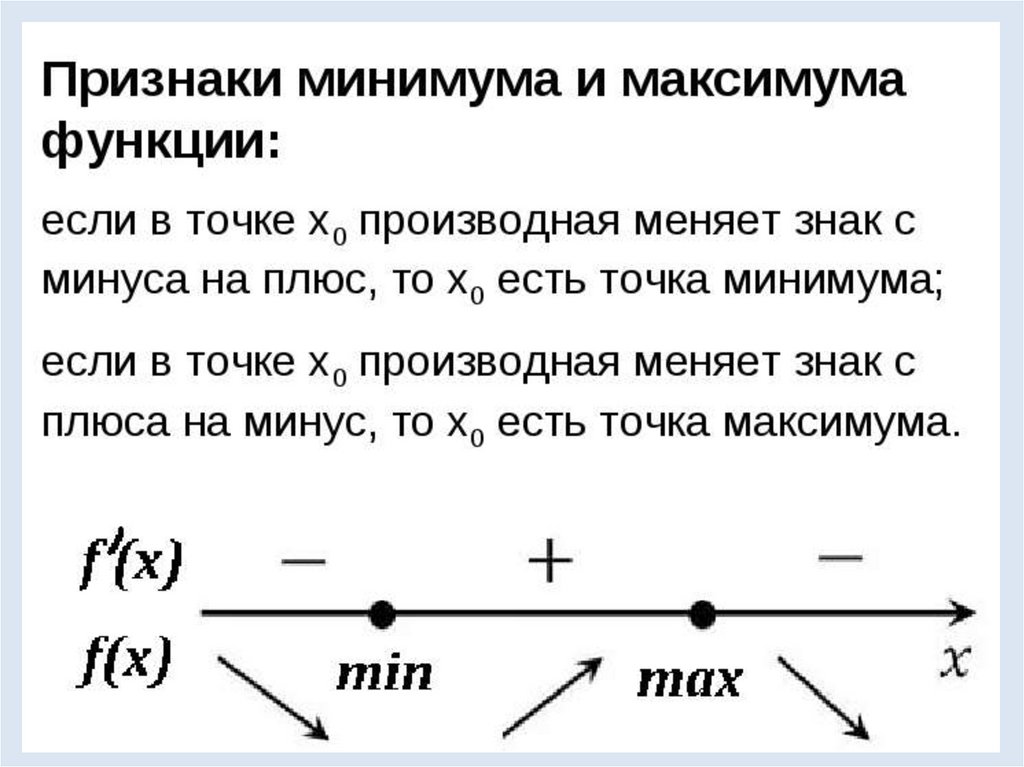
Пусть xо точка из области определения
функции f(x) и f′ (xо) = 0, если производная
функции меняет свой знак с «+» на «-» в
точке x о или наоборот, то эта точка
является Экстремумом.

15. ё

16.

17.

18.

19.

20.

Задание 1

21. Задание1. Исследовать функцию на монотонность

22. Решение:

23. Задание 2. Исследовать функцию на монотонность

24. Решение:

25. Самостоятельная работа

1. Найдите точки экстремума функции.
у=3х4-16х3+24х2-11
2. Определите промежуток монотонности
функции у=х2 -8х +5

26. Домашнее задание

• - сделать конспект лекции.
• - решить самостоятельно примеры (в конце)
• - для закрепления посмотреть видео урок
по ссылке
https://www.youtube.com/watch?v=jhKDxT
1fwkQ

27.

28. Спасибо за внимание