Призма. Как открыли призму?

1.

Презентация на тему:
«Призма»

2.

Призма
Многогранник,
составленный из двух
равных многоугольников
A1A2…An и B1B2…Bn,
расположенных в
параллельных
плоскостях, и n
параллелограммов,
называется призмой
Bn
B1
B3
B2
An
A1
A3
A2

3.

Как открыли призму
Термин “призма” греческого происхождения и буквально означает “отпиленное”
(тело) . Термин “параллелепипедальное тело” встречается впервые у Евклида и
означает дословно “параллеле-плоскостное тело”. Греческое слово “кубос”
употребляется Евклидом в том же смысле, что и наше слово “куб”
Евклид определяет призму как телесную фигуру, заключенную между двумя равными
и параллельными плоскостями (основаниями) и с боковыми гранями параллелограммами. В XVIII в. Тейлор дал такое определение призмы: это
многогранник, у которого все грани, кроме двух, параллельны одной прямой.
В памятниках вавилонской и древнеегипетской архитектуры встречаются такие
геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей
египетской и вавилонской геометрии было определение объема различных
пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы,
храмы и другие сооружения.

4.

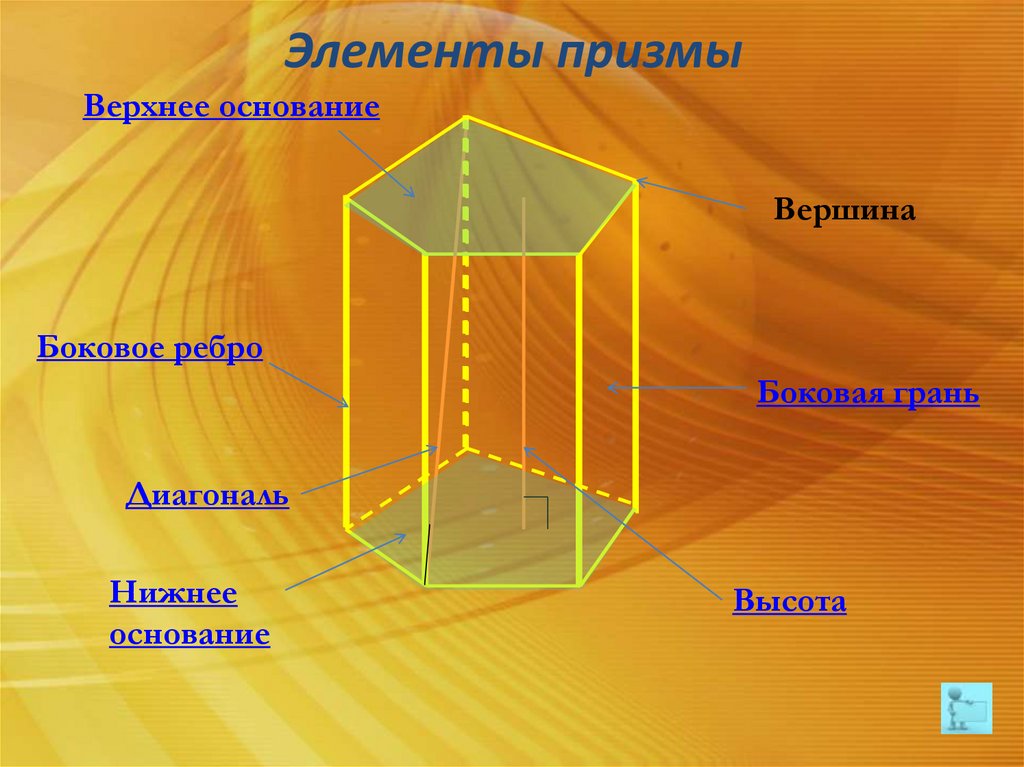
Элементы призмы
Верхнее основание
Вершина
Боковое ребро
Боковая грань
Диагональ
Нижнее
основание
Высота

5.

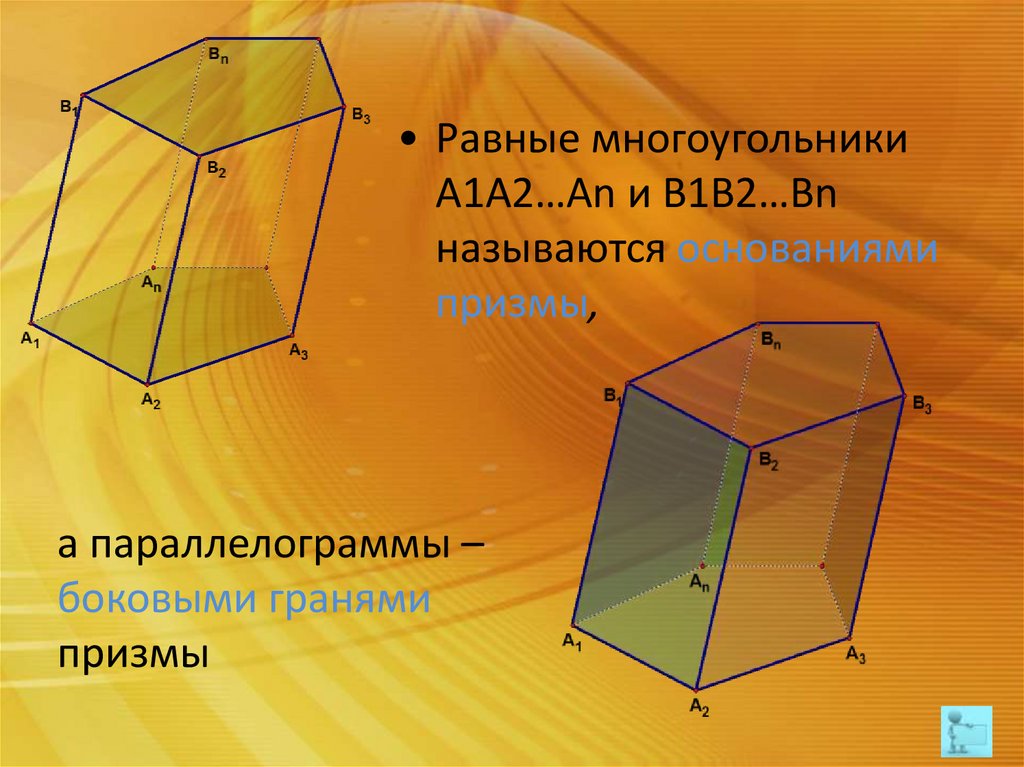
• Равные многоугольники
A1A2…An и B1B2…Bn
называются основаниями
призмы,
а параллелограммы –
боковыми гранями
призмы

6.

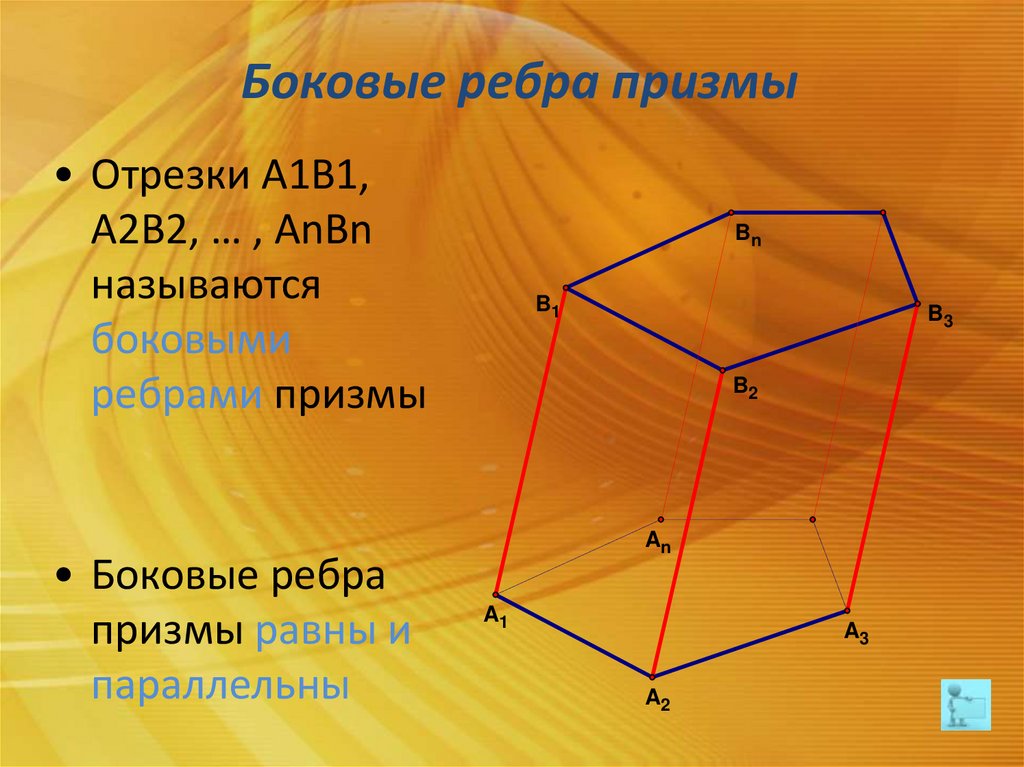
Боковые ребра призмы
• Отрезки A1B1,
A2B2, … , AnBn
называются
боковыми
ребрами призмы
• Боковые ребра
призмы равны и
параллельны
Bn
B1
B3
B2
An
A1
A3
A2

7.

Высота призмы
Bn
B1
B3
B2
An
A1
M
A3
A2
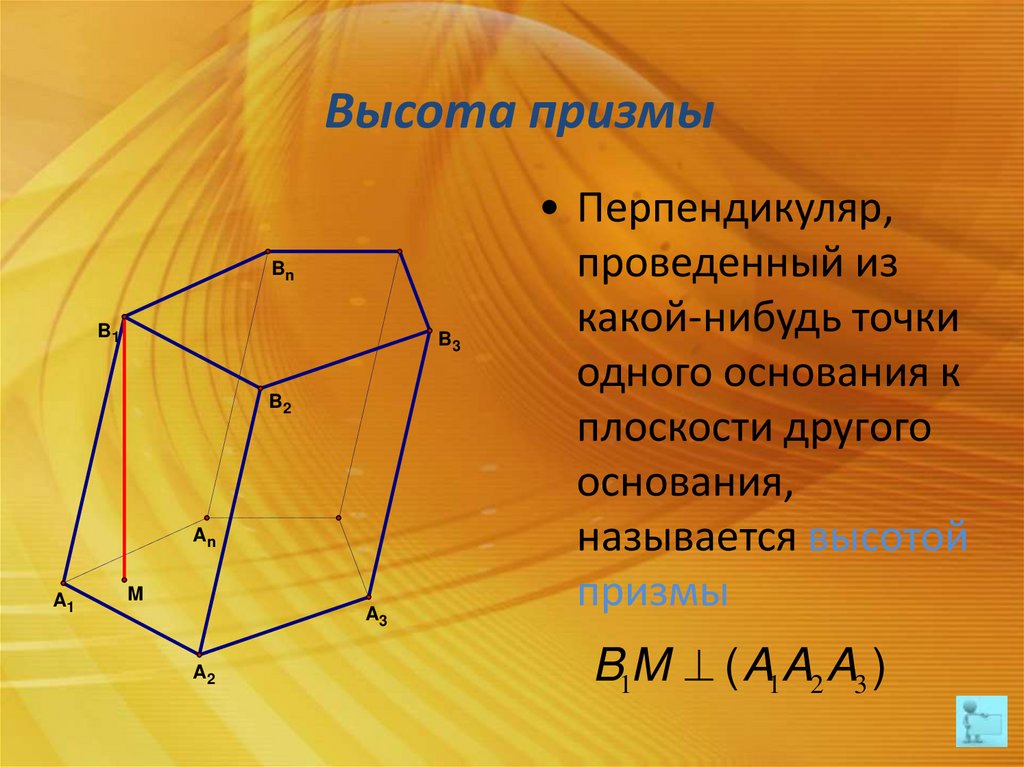
• Перпендикуляр,
проведенный из
какой-нибудь точки
одного основания к
плоскости другого
основания,
называется высотой
призмы
B1M ( A1A2 A3 )

8.

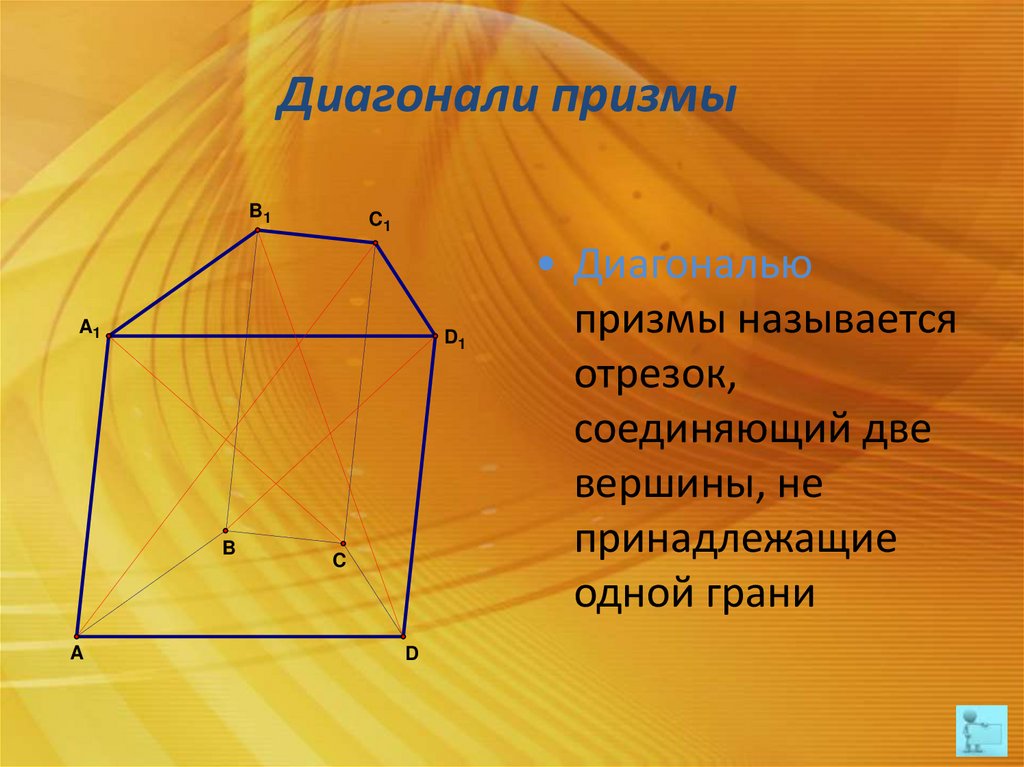
Диагонали призмы
B1
C1
A1
D1
B
A
C
D
• Диагональю
призмы называется
отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани

9.

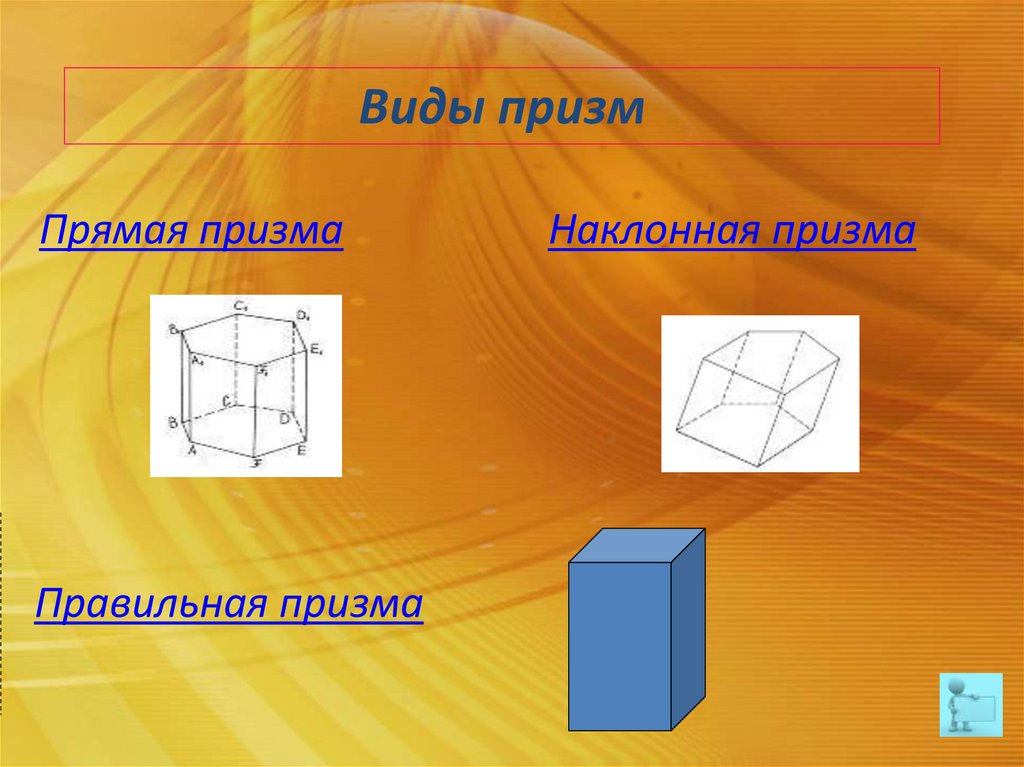
Виды призм
Прямая призма
Правильная призма
Наклонная призма

10.

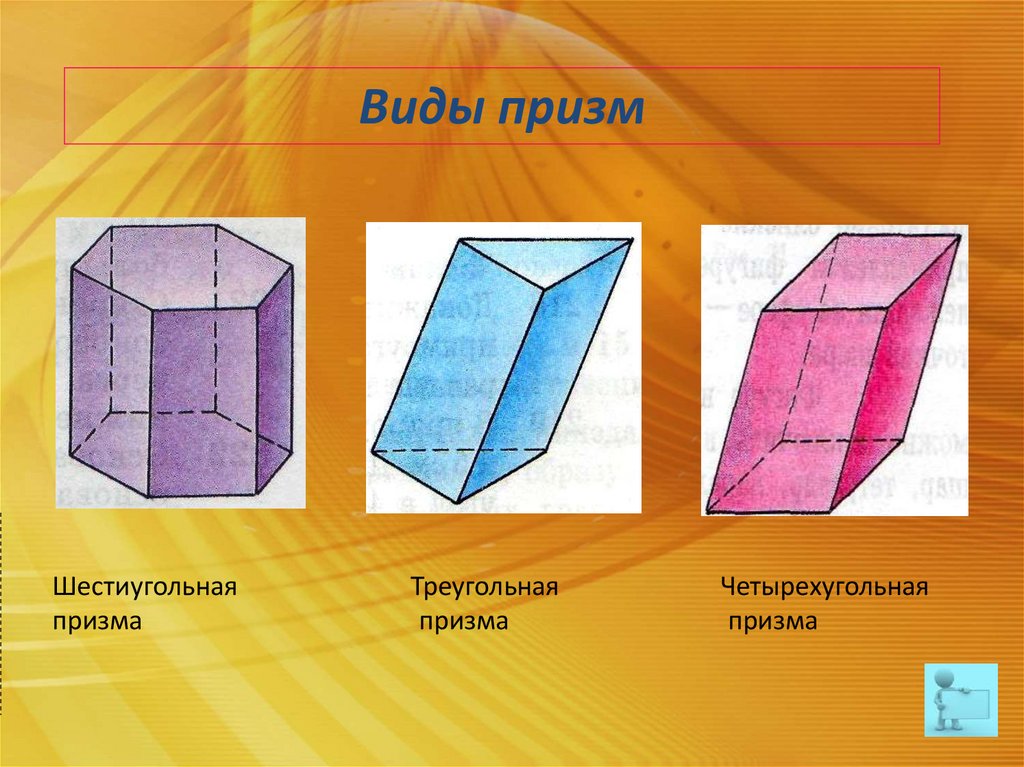
Виды призм
Шестиугольная
призма
Треугольная
призма
Четырехугольная
призма

11.

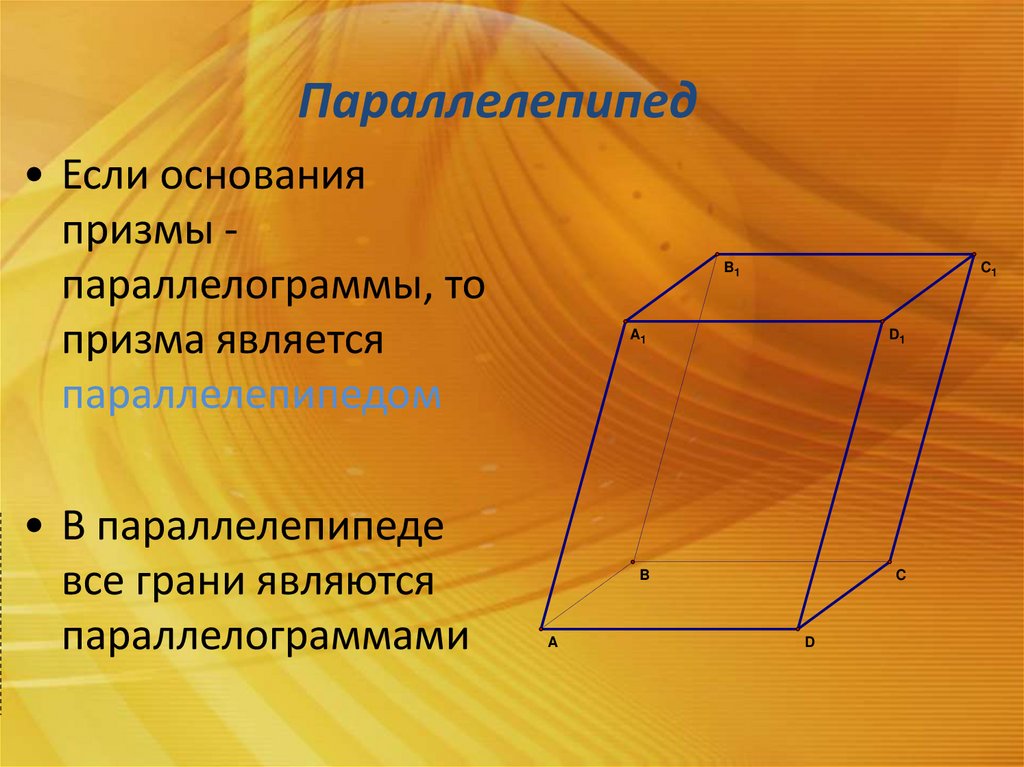
Параллелепипед
• Если основания
призмы параллелограммы, то
призма является
параллелепипедом
• В параллелепипеде
все грани являются
параллелограммами
C1
B1
A
A1
D1
B
C
D

12.

Прямая и наклонная призмы
• Если боковые ребра призмы перпендикулярны к
основаниям, то призма называется прямой,
• в противном случае – наклонной
• Высота прямой призмы равна её боковому ребру

13.

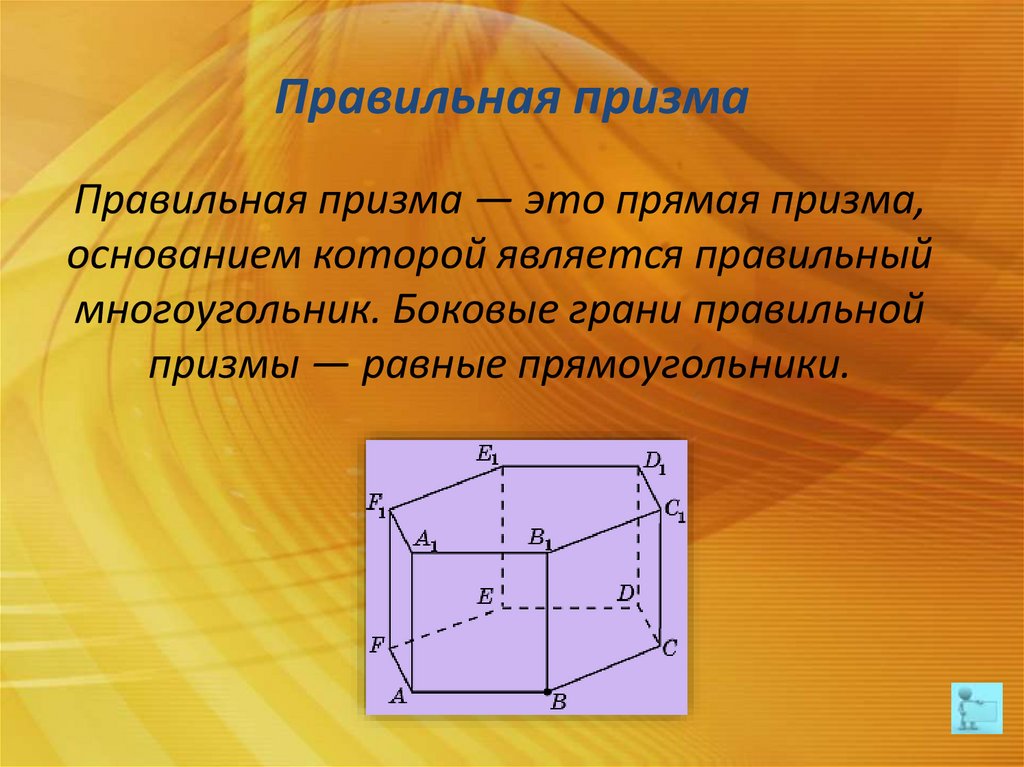
Правильная призма
Правильная призма — это прямая призма,
основанием которой является правильный
многоугольник. Боковые грани правильной
призмы — равные прямоугольники.

14.

Площадь поверхности призмы
• Площадью полной поверхности призмы
называется сумма площадей всех её
граней Sполн
• Площадью боковой поверхности призмы
называется сумма площадей её боковых
граней S
бок
Sполн Sбок 2Sосн

15.

Теорема о площади боковой
поверхности прямой призмы
Теорема.
Площадь боковой поверхности прямой
призмы равна произведению периметра
основания на высоту призмы
Sбок Pосн H

16.

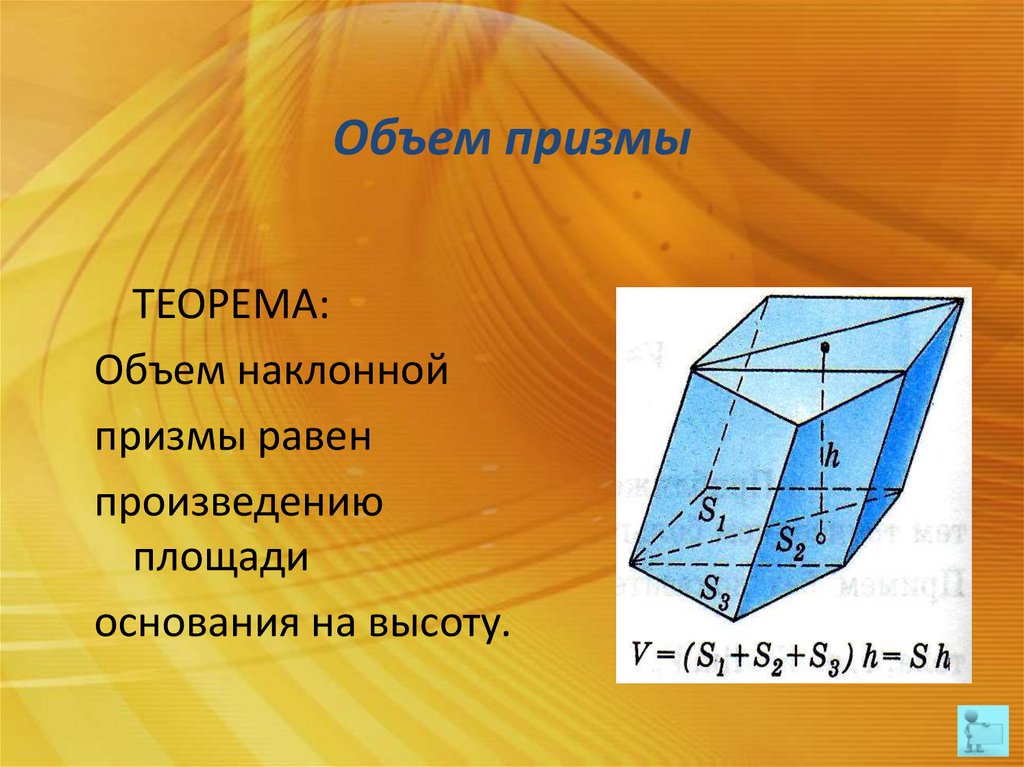
Объем призмы
ТЕОРЕМА:
Объем наклонной
призмы равен
произведению
площади
основания на высоту.

17.

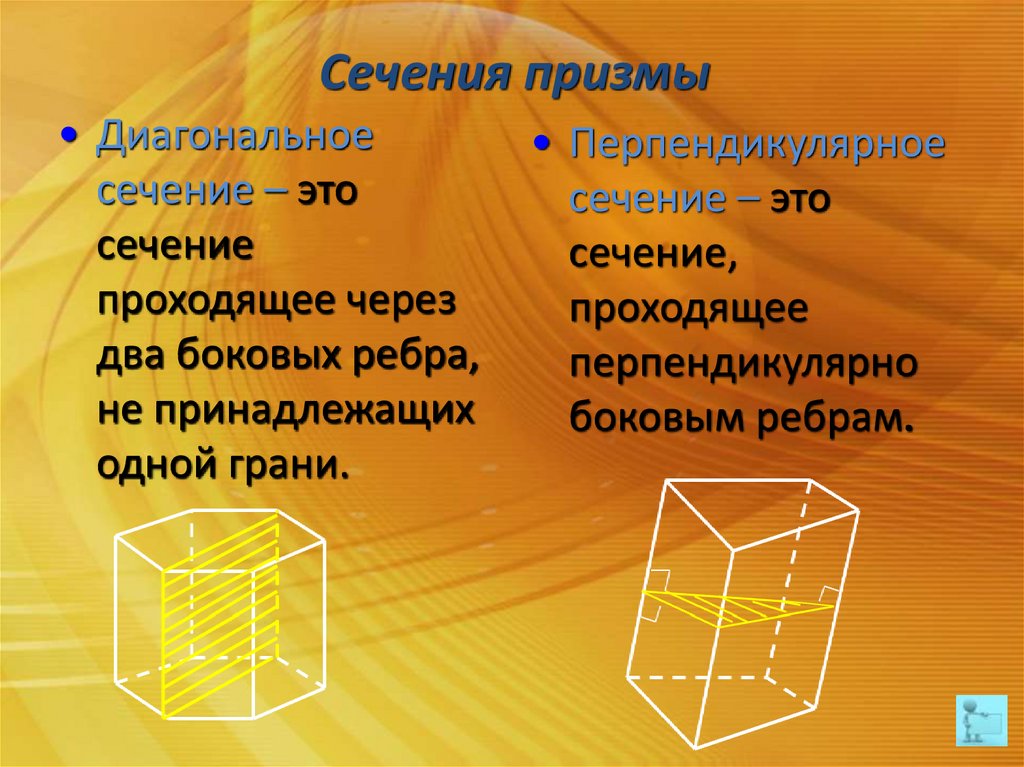
Сечения призмы
• Диагональное
сечение – это
сечение
проходящее через
два боковых ребра,
не принадлежащих
одной грани.
• Перпендикулярное
сечение – это
сечение,
проходящее
перпендикулярно
боковым ребрам.

18.

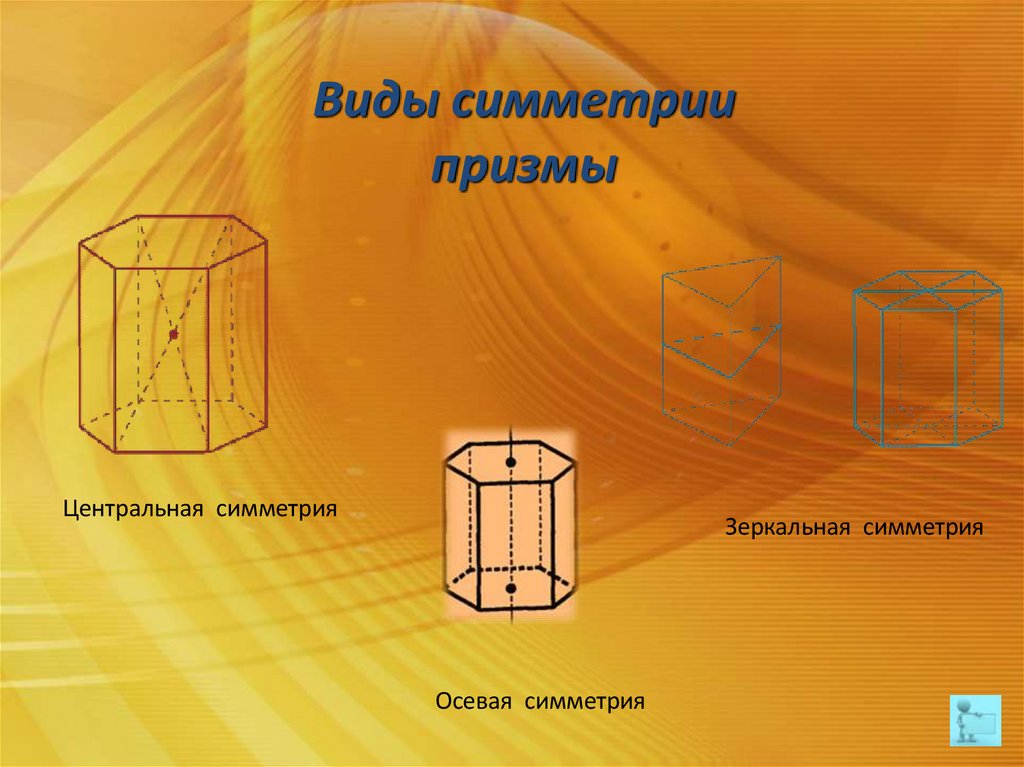
Виды симметрии
призмы
Центральная симметрия
Зеркальная симметрия
Осевая симметрия

19.

Задача №1.
Дано: Сторона основания правильной треугольной
призмы равна 8 см, боковое ребро - 6 см. Найдите
Sсеч, проходящего через сторону верхнего основания
и противолежащую вершину нижнего основания.

20.

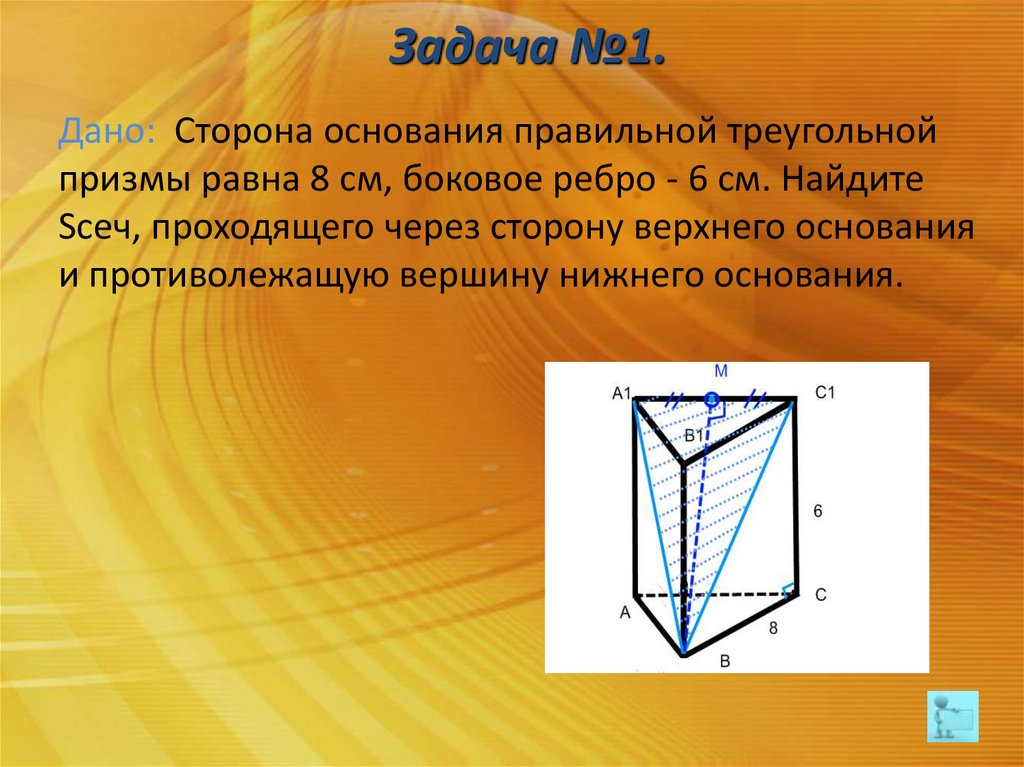
Задача №1.
Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое
ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и
противолежащую вершину нижнего основания.
Решение: Треугольник A1B1C1 –
равносторонний (A1B=C1B как
диагональ равных граней)
1)Рассмотрим треугольник BCC1–
прямоугольный
BC1*2=BM*2+CC1*2( по теореме
Пифагора)
BC1= √ 64+36=10 см
2) Рассмотрим треугольник BMC1–
прямоугольный
BC1*2=BM*2+MC1*2
BM*2=BC1*2-MC1*2
BM*2=100-16=84
BM= √ 84=2 √ 21 см
3) Sсеч=1/2 (A1C1*BM)=8 √ 21см*2

21.

Задача №2.
Основанием прямой призмы
является равнобедренная
трапеция с основаниями 21см и
9 см и высотой 8 см (рис. 1).
Найдите площадь боковой
поверхности, если боковое
ребро равно 10 см.

22.

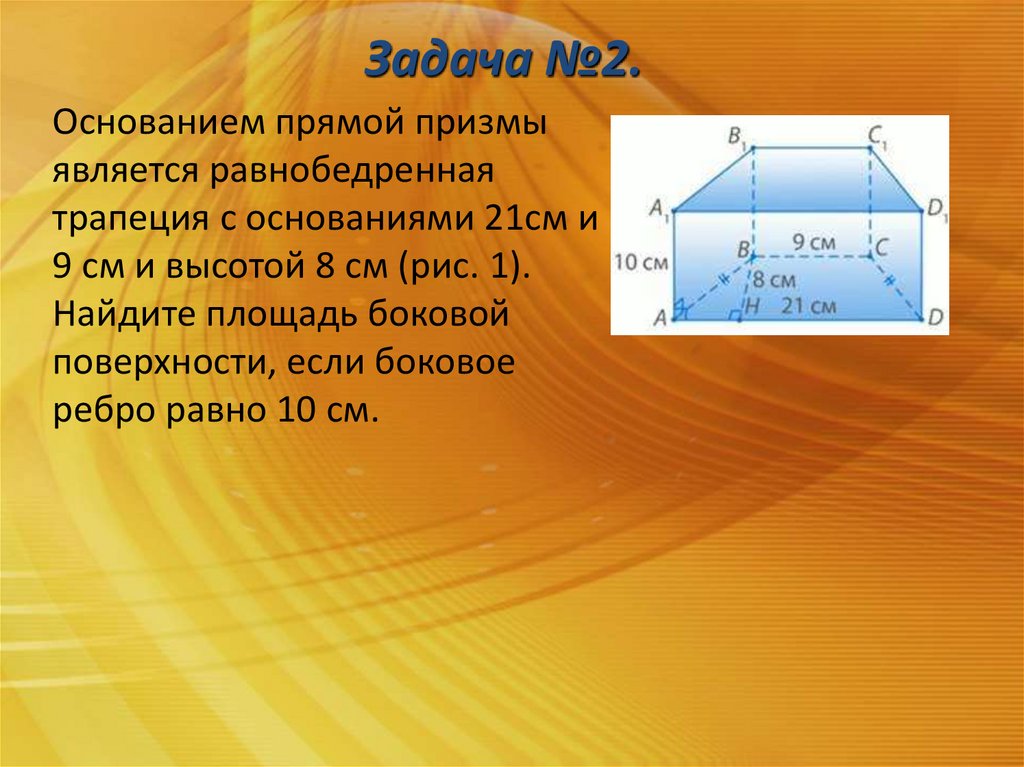
Задача №2.
Основанием прямой призмы является равнобедренная
трапеция с основаниями 21см и 9 см и высотой 8 см .
Найдите площадь боковой поверхности, если боковое ребро
равно 10 см.
Рис. 1
Дано: прямая призма АВСDА1В1С1D1, в основании
равнобедренная трапеция АВСD
AD = 21см, BC = 9см, BH = 8 см,
АА1 ⊥ АВС, АА1 = 10 см.
Найти: Sбок
Решение:
Рассмотрим трапецию ABCD . ВН и CG – высоты трапеции. AD =
21см, BC = 9см. Так как трапеция ABСD равнобедренная тогда
АH=GD и HG = BC = 9 см, (см).
Рис. 2
Рассмотрим треугольник ∆АВН и найдем сторону АВ по теореме
Пифагора:
Найдем периметр основания.
Применяем формулу для площади боковой поверхности:
Ответ: 500 см2

23.

Призмы вокруг нас