Similar presentations:
Уравнения высших степеней, приводимые к виду квадратного уравнения
1.
Уравнения высшихстепеней, приводимые к
виду квадратного
уравнения
2.
Методы решенияуравнения высших
степеней
• Разложение
на
множители
Введение
новой
переменной
Графический
способ
3.
РАЗЛОЖЕНИЕ НАМНОЖИТЕЛИ
• Способ
группировки
С помощью формул
сокращенного
умножения
По теореме
Безу
4.
Разложение на множители методом группировки иформул сокращенного умножения
Основа данного метода также не нова
и заключается в группировке
слагаемых таким образом, чтобы
каждая группа содержала общий
множитель. Для этого иногда
приходится применять некоторые
искусственные приемы.
5.
Пример1.х 5 х 4 3х 3 2 х 2 2 х 6 0
Решение:
Пропорциональность коэффициентов многочлена дает
возможность сгруппировать слагаемые в левой части уравнения :
х х 3х 2 х 2 х 6 0,
х х х 3 2 х х 3 0, х 2 х х 3 0. Получаем
5
3
4
2
3
2
2
3
2
совокупность двух уравнений
х 3 2 0, х 2 х 3 0.
Таким образом, корнями уравнения являются действительные числа :
1 13
х1 2 , х2,3
.
2
3
6.
Пример 2.Решите уравнение с помощью
разложения на множители.
7.
Пример 3.х 3 х 4 х 3 0.
4
Решение:
2
Представим 3х 2 2 х 2 х 2 и сгруппируем :
х 2 х х 4 х 3 0.
х 2 х 1 1 х 4 х 3 1 1 0.
х 1 1 х 2 1 0.
х 1 х 2 0.
х 1 х 2 х 1 х 2 0.
х х 1 х х 3 0.
4
2
4
2
2
2
2
2
2
2
2
2
2
2
2
2
х 2 х 1 0 или х 2 х 3 0.
1 13
Ответ : В первом уравнении нет корней, из второго : х1, 2
.
2
8.
Парная работа№
№
9.
Индивидуальная работаРешите уравнения методом разложения на
множителей:
1. х х 6 х 0
4
3
2
2. х 5 х 5 х 1 0
3
2
10.
1. х х 6 х 04
3
2
х х х 6 0
2
2
x1 0
х х 6 0
2
x2 2
x3 3
Ответ : 3;0;2
11.
2. х 5 х 5 х 1 03
2
х 1 5х х 1 0
х 1 x 4 x 1 0
3
2
x1 1
x 4x 1 0
2
x2 2 3
x3 2 3
Ответ : 1;2 3;2 3
12.
Домашнее задание№34.2(3; 4) №34.7(1; 3)








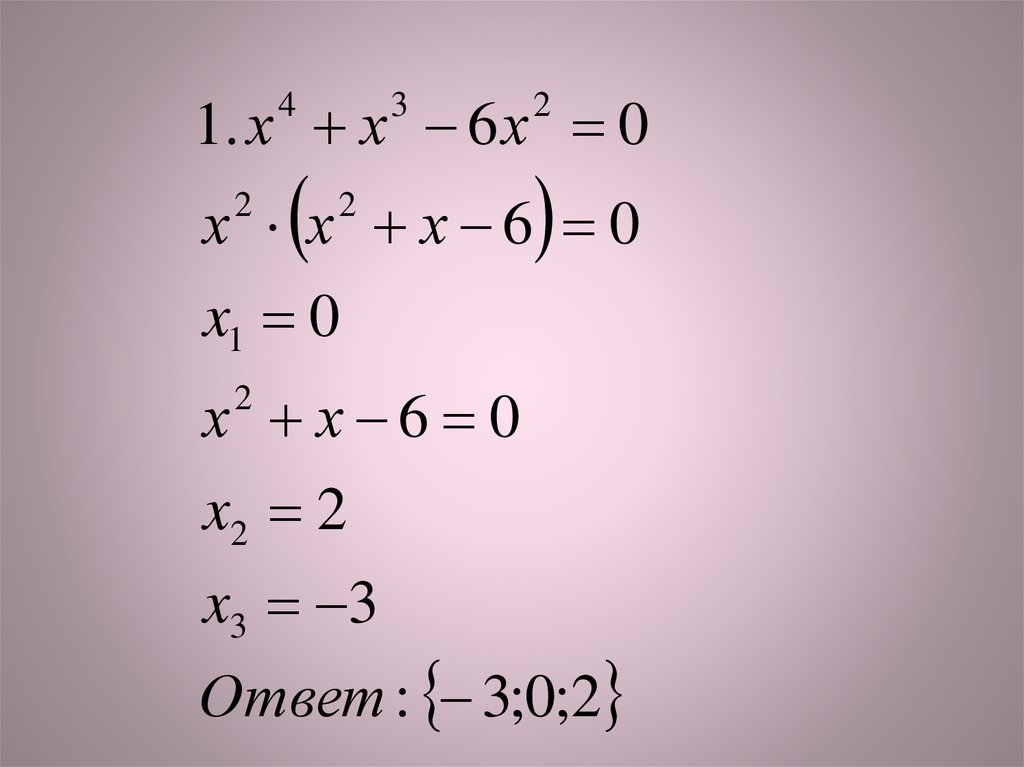
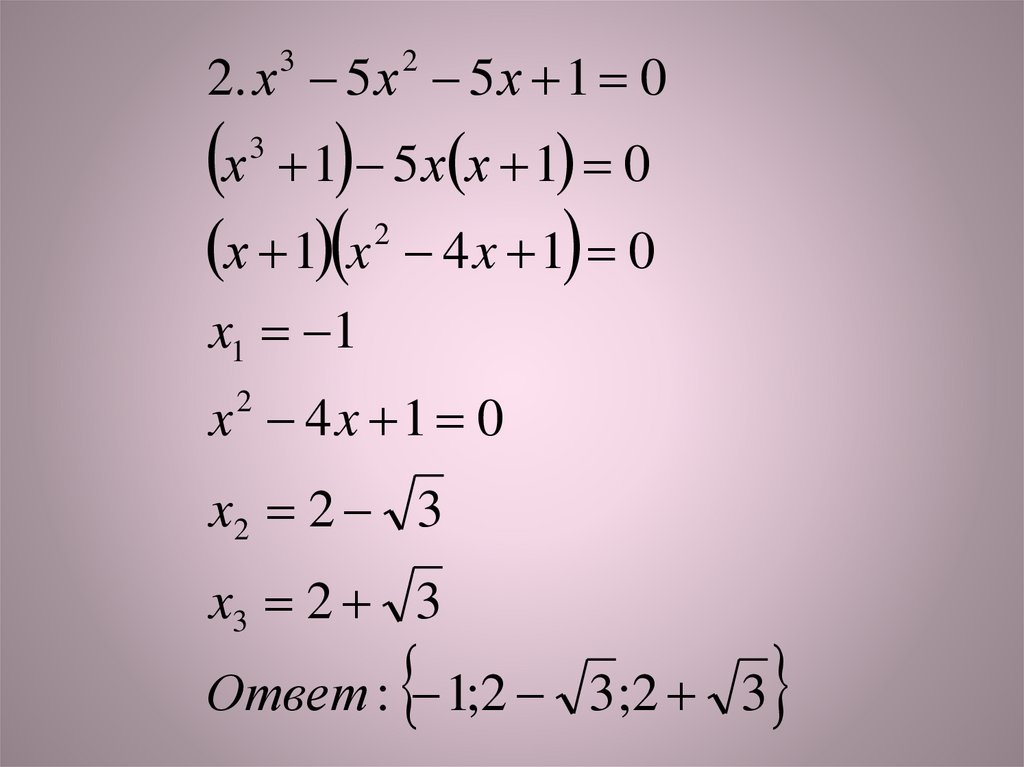

 mathematics
mathematics