Similar presentations:
Уравнения, приводимые к квадратным
1. ГБОУ ШКОЛА № 489 Московского района г. С-Петербурга
Урок по алгебре в 9 классеУравнения, приводимые
к квадратным.
Выполнила: учитель математики
Большакова Е.Н.
2.
Девиз урока:«Чем больше я знаю,
тем больше умею.»
3. Эпиграф
Кто ничего не замечает,Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
(поэт Р.Сеф).
4. Повторенье - Мать Ученья
Что называется целым уравнением с однойпеременной?
Что называется степенью целого уравнения?
Сколько корней может иметь целое уравнение с
одной переменной 2-ой, 3-ей, 4-ой, п-ой степени
Какие виды целых уравнений вам знакомы?
Какие способы решения уравнений вы знаете?
5. Объяснить метод решения каждого из уравнений:
1.2.
3.
4.
5.
6.
2
х – 5х = 0
2
5х– 2х + 6 = 0
3
х = 2х + 2
3
2
х + 2х – 3х = 0
2
2
( х + 3х + 2 ) (х + 3х + 4 ) = 4
4
2
х – 5х– 36 = 0
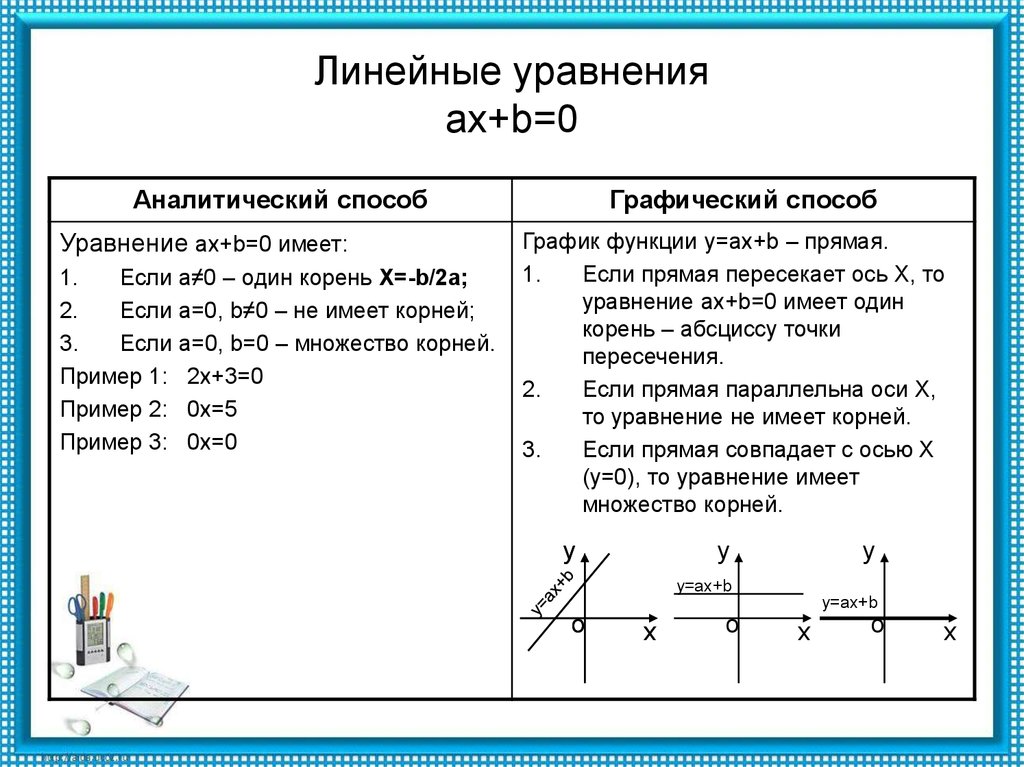
6. Линейные уравнения ax+b=0
Аналитический способУравнение ax+b=0 имеет:
1.
Если а≠0 – один корень X=-b/2a;
2.
Если a=0, b≠0 – не имеет корней;
3.
Если a=0, b=0 – множество корней.
Пример 1: 2х+3=0
Пример 2: 0х=5
Пример 3: 0х=0
Графический способ
График функции у=ах+b – прямая.
1.
Если прямая пересекает ось Х, то
уравнение ах+b=0 имеет один
корень – абсциссу точки
пересечения.
2.
Если прямая параллельна оси Х,
то уравнение не имеет корней.
3.
Если прямая совпадает с осью Х
(у=0), то уравнение имеет
множество корней.
у
у
у
у=ах+b
о
х
о
у=ах+b
х
о
х
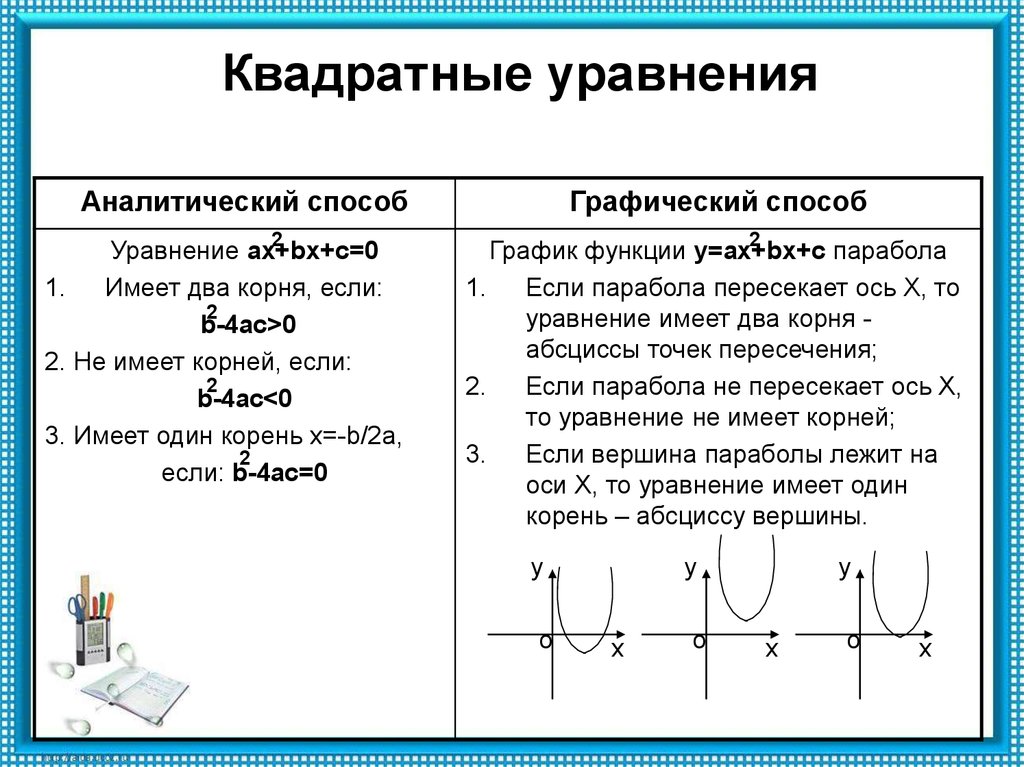
7.
Квадратные уравненияАналитический способ
2
Уравнение ax+bx+c=0
1. Имеет два корня, если:
2
b-4ac>0
2. Не имеет корней, если:
2
b-4ac<0
3. Имеет один корень х=-b/2а,
2
если: b-4ac=0
Графический способ
2
График функции у=ax+bx+c
парабола
1. Если парабола пересекает ось Х, то
уравнение имеет два корня абсциссы точек пересечения;
2.
Если парабола не пересекает ось Х,
то уравнение не имеет корней;
3. Если вершина параболы лежит на
оси Х, то уравнение имеет один
корень – абсциссу вершины.
у
о
у
х
о
у
х
о
х
8.
Алгоритм решения биквадратногоуравнения
1. Ввести замену переменной.
2. Составить квадратное уравнение с новой
переменной.
3. Решить новое квадратное уравнение.
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные
уравнения.
6. Сделать вывод о числе решений уравнения.
7. Записать ответ.
9.
Метод введения новой переменной2
2
(х + 3х + 2)(х + 3х + 4) = 48
1 шаг Ввести новую переменную t,
которая обозначает повторяющееся
выражение х 2+ 3х. Записать
получившееся уравнение.
2
Пусть t = х + 3х, тогда
(t + 2)(t + 4) = 48
2
2 шаг
Решить уравнение относительно
новой переменной.
t + 4t + 2t + 8 – 48 = 0
2
t + 6t – 40 = 0
t 1= -10; t 2= 4
3 шаг
Вернуться к первоначальной
х+3х=-10 или х+3х = 4
2
2
переменной Х, подставив найденное х+3х+10=0
х+3х-4=0
значение вместо переменной t.
Д=9-40=-31
х=1; х=-4
1
2
Д<0, корней нет
Ответ: -4; 1
2
2
10.
Запишите уравнение, полученное врезультате введения новой переменной
(7х2+2х–3)(7х2+2х+5)=16 (х2+3х+1)2+4(х2+3х+1)–6 = –1
пусть t =_______,
пусть t =_______,
тогда_____________
тогда_____________
(3х–5)2 – 4(3х2–5)=12
пусть t =_______,
тогда_____________
(3х2+5х+2)(3х2+5х–5) –5=16
пусть t =_______,
тогда_____________
х4 – 25х2 + 144 = 0
пусть t =_______,
тогда_____________
16х4 – 8х2 + 1 = 0
пусть t =_______,
тогда_____________
11.
Запишите уравнение, полученное врезультате введения новой переменной
(7х2+2х–3)(7х2+2х+5)=16 (х2+3х+1)2+4(х2+3х+1)–6 = –1
пусть t =_______,
пусть t =х2+3х+1,
тогда_____________
тогда t2+4t-6=-1
(3х–5)2 – 4(3х2–5)=12
пусть t =_______,
тогда_____________
(3х2+5х+2)(3х2+5х–5) –5=16
пусть t =3х2+5х,
тогда (t+2)(t-5)-5=16
х4 – 25х2 + 144 = 0
пусть t =_______,
тогда_____________
16х4 – 8х2 + 1 = 0
пусть t =х2,
тогда16t2-8t+1=0
12. Физкультминутка
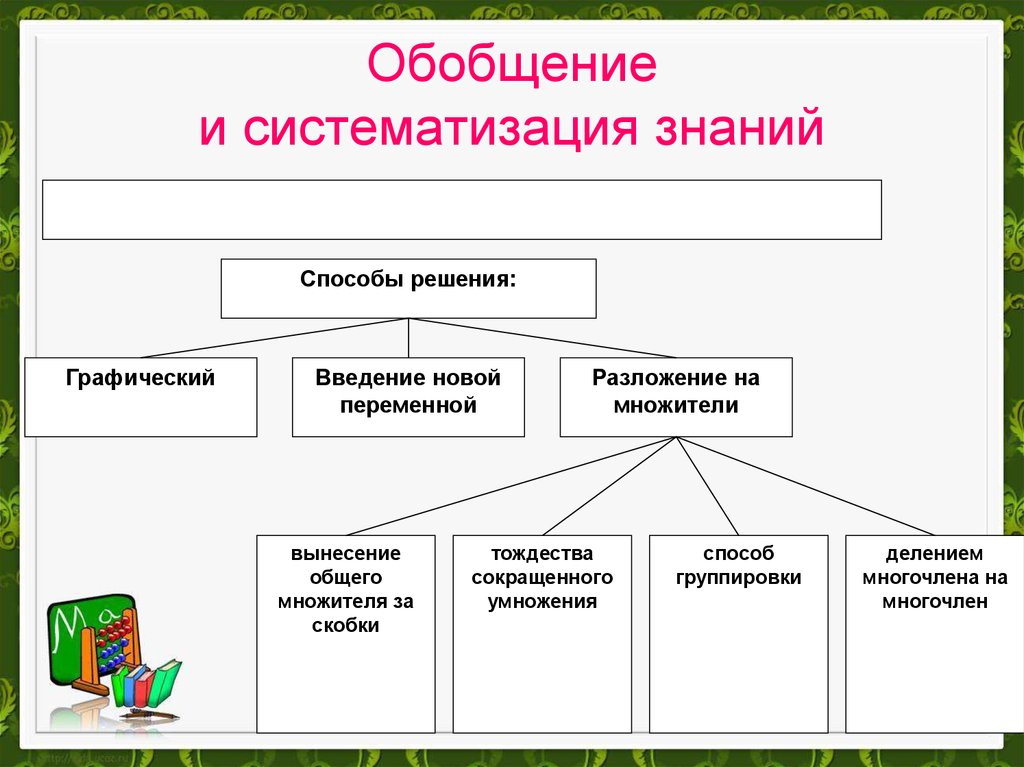
13. Обобщение и систематизация знаний
Способы решения:Графический
Введение новой
переменной
вынесение
общего
множителя за
скобки
Разложение на
множители
тождества
сокращенного
умножения
способ
группировки
делением
многочлена на
многочлен
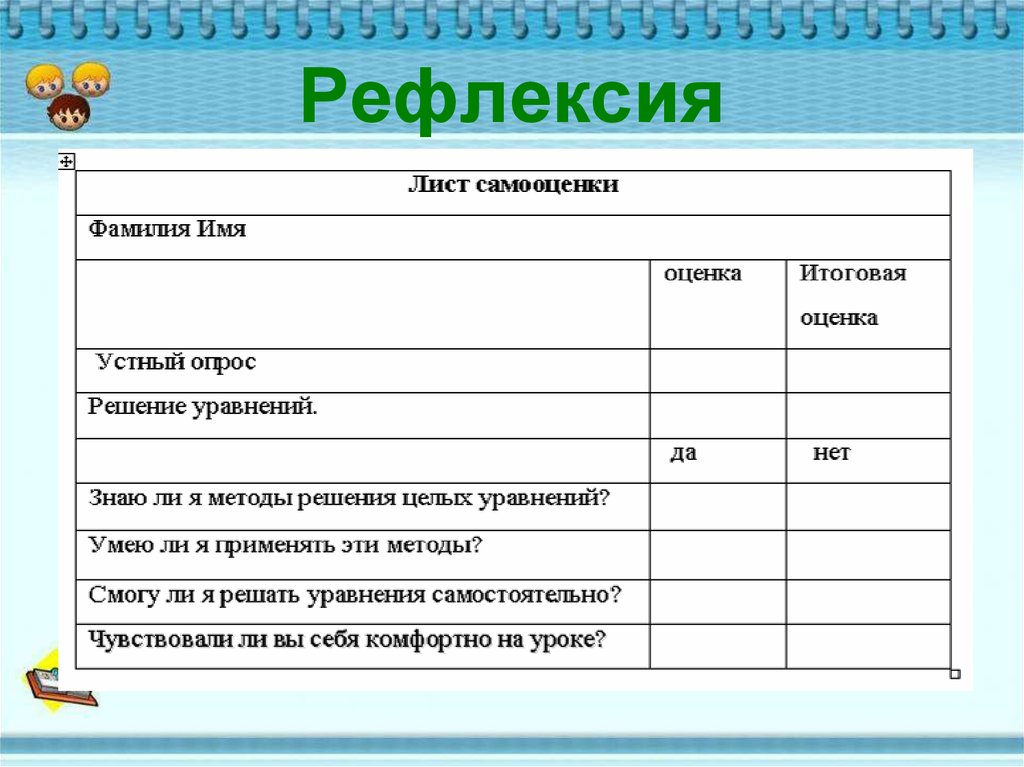
14. Рефлексия
15. Домашняя работа
1. Учебник «Алгебра 9», автор Алимов Ш.А.,задание № 622 (2;4).
2. Сборник заданий «ГИА-2012», вариант 4,
задание № 19.
3. Дидактические материалы «Алгебра 8»,
автор Зив Б.Г.,
самостоятельная работа № 12, вариант 3 (3а)












 mathematics
mathematics