The binomial, hypergeometric, poisson distributions (lecture 8)

1.

LECTURE 8
THE BINOMIAL, HYPERGEOMETRIC,
POISSON DISTRIBUTIONS
&
CONTINOUS RANDOM VARIABLES

2.

THE BINOMIAL DISTRIBUTION

3.

THE BINOMIAL DISTRIBUTION

4.

THE BINOMIAL DISTRIBUTION

5.

Ex: People who work at high-stress jobs frequently develop stress-related physical problems. In a recent study,
it was found that 40% of the large number of business executives surveyed have symptoms of stress-induced
problems. Consider a group of 1500 randomly selected business executives and assume that the probability of
an executive with stress-induced problems is 0.4.
Let X be the number of business executives in the sample of 1500 who develop stress-related problems. What
are the mean and standard deviation of X?

6.

Ex: If for a binomial random variable, the probability of success in one trial is 0.25, what’s the
probability of 8 success in 20 trials?

7.

THE HYPERGEOMETRIC DISTRIBUTION

8.

Ex: A company receives a shipment of 20 items. Because inspection of each individual item is expensive, it has
a policy of checking a random sample of 6 items from such a shipment and accepting delivery if no more than
one sampled item is defective. What is the probability that a shipment with 5 defective items will b e
accepted?

9.

THE POISSON DISTRIBUTION

10.

Ex: Customers arrive at a photocopying machine at an average rate of 2, every five minutes. Assuming that
this arrival process has a Poisson distribution, what’s the proability of more than 2 arrivals in five minutes
period?

11.

CONTINOUS RANDOM VARIABLES
AND
PROBABILITY DISTRIBUTIONS

12.

CONTINOUS RANDOM VARIABLES
Continuous Random Variables: the variables that can take any value on a continuum.
Measures of time, distance or temperature
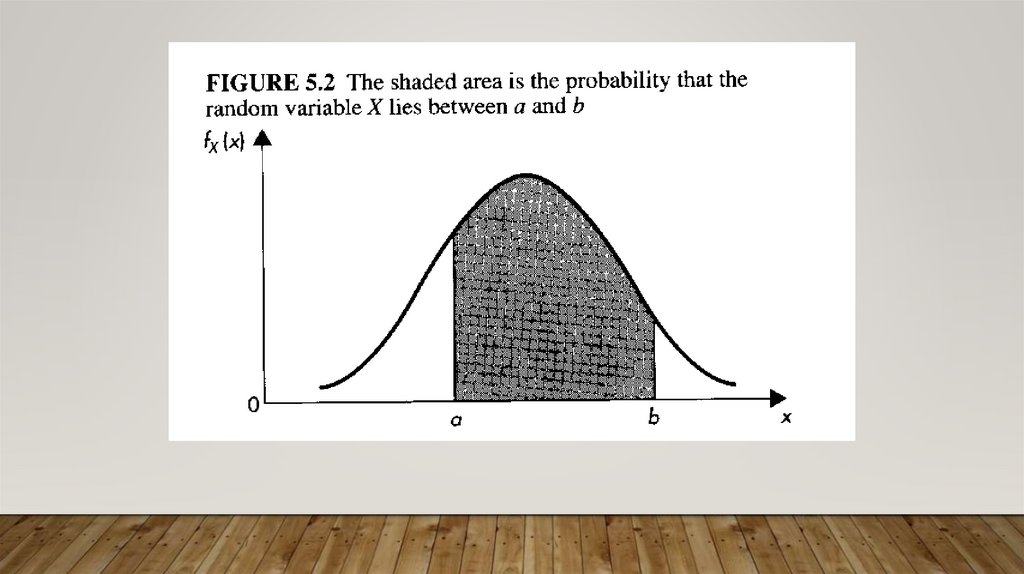
A natural place to begin to analyze the probability distributions of continuous random variables is
using the idea of cumulative probability.

13.

PROBABILITY DISTRIBUTIONS FOR
CONTINUOUS RANDOM VARIABLES

14.

15.

Ex:

16.

17.

PROBABILITY DISTRIBUTIONS FOR CONTINUOUS RANDOM VARIABLES

18.

Ex: A salesman receives an annual salary of $6,000, plus %8 of the value of the orders he takes. The annual
value of these orders can be represented by a random variable with mean $600,000 and standard deviation
$180,000. Find the mean and standard deviation of the salesman’s annual income.

19.

JOINTLY DISTRIBUTED CONTINUOUS RANDOM VARIABLES

20.

21.

SUMS AND DIFFERENCES OF CONTINOUS RANDOM VARIABLES

22.

THE NORMAL DISTRIBUTION
The normal distribution which is a continous distribution plays a central role in a very large body of
statistical analysis.

23.

THE NORMAL DISTRIBUTION
• As an example, suppose that a big group of students takes a test. A large proportion of their scores are
likely to be concentrated about the mean and the numbers of scores in ranges of a fixed width are
likely to ‘tail off’ away from the mean. If the average score on the test is 60, we would expect to find, for
instance, more students with scores in the range 55 – 65 than in the range 85 – 95.
• These considerations suggest a probability density function that peaks at the mean and tails off at its
extremities. One distribution with these properties is the normal distribution.

24.

PROBABILITY DENSITY FUNCTION OF THE
NORMAL DISTRIBUTION

25.

SOME PROPERTIES OF THE NORMAL DISTRIBUTION

26.

NOTATION

27.

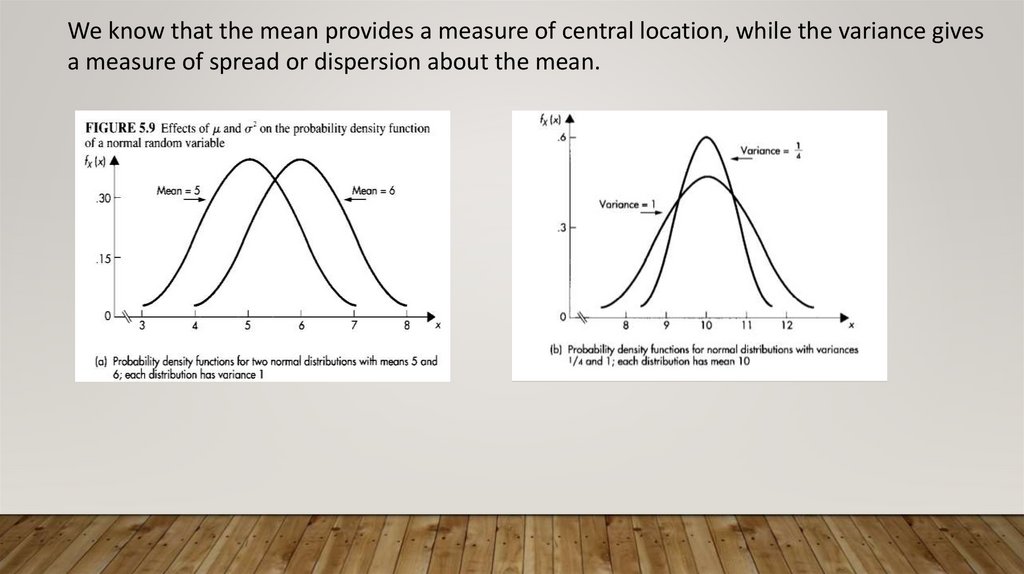
We know that the mean provides a measure of central location, while the variance gives
a measure of spread or dispersion about the mean.

28.

CUMULATIVE DISTRIBUTION FUNCTION OF THE NORMAL
DISTRIBUTION

29.

THE STANDARD NORMAL DISTRIBUTION

30.

FINDING RANGE PROBABILITIES FOR NORMAL
RANDOM VARIABLES