Матрицы и действия над ними

1.

1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ

2. ОПРЕДЕЛЕНИЕ МАТРИЦЫ

МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНАЯ ИЛИ
КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ
ЧИСЛАМИ.
Обозначение A, В, С ,...
1 1 4
Пример: A
2 3 2
Число строк – m
Число столбцов – n
Размерность матрицы m n
2 3

3. Элементы матриц

- числа, заполняющие матрицу.
Обозначение:
A aij
i – номер строки, нумеруются сверху вниз
j – номер столбца, нумеруются слева направо
a11 a12
a21 a22
...
...
a
m1 am 2
... a1n
... a2 n
... ...
... amn
Пример:
a
1
11
1 1 4
A
2 3 2 a23 2

4. ВИДЫ МАТРИЦ

3
4
12
22
17 29 Прямоугольная Матрица-столбец
0
матрица
30 36
5
3 1 2
4 2 0 Квадратная
матрица
5 6 1
1 3 2
0
Матрица-строка

5. ВИДЫ МАТРИЦ

3 1 2
4 2 0 Главная диагональ
5 6 1
3 1 2
4 2 0 Побочная диагональ
5 6 1

6. ТРЕУГОЛЬНЫЕ МАТРИЦЫ

Верхняя треугольная матрица
3 1 2
0 2 0 (под главной диагональю стоят нули)
0 0 1
Нижняя треугольная матрица
3 0 0
1 2 0 (над главной диагональю стоят нули)
2 0 1

7. ОПЕРАЦИИ НАД МАТРИЦАМИ

8. УМНОЖЕНИЕ НА ЧИСЛО

A aij
3 1 2 15 5 10
5 4 2 0 20 10 0
5 6 1 25 30 5

9. СЛОЖЕНИЕ, ВЫЧИТАНИЕ

A B aij bij
3 1 2
А
4 2 0
8 5 5
В
7 3 14
3 8 1 ( 5) 2 5 11 6 7
А В
2 3
0 14 11 5 14
4 7
3 8 1 ( 5) 2 5 5 4 3
А В
2 3
0 14 3 1 14
4 7
Операции возможны только с матрицами одинаковой
размерности

10. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ

А аij A a ji
T
4
12
Исходная
A 17 29
матрица (размер 3 на 2)
30 36
12 17 30 Транспонированная
A
матрица (размер 2 на 3)
4
29
36
T

11.

→
→

12. УМНОЖЕНИЕ МАТРИЦЫ НА МАТРИЦУ

МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО
УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И
ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ
МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК
МАТРИЦЫ B

13. ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ

С A B
A левая матрица, B правая матрица

14. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ

3 1 2 8 1
4 2 0 7 2
5 6 1 2 3
3 8 1 7 2 2 3 1 1 2 2 3 21 5
4 8 2 7 0 2
4 1 2 2 0 3 46 8
5 8 6 7 1 2 5 1 6 2 1 3 4 4
Замечание.
Обратное действие невозможно!
В общем случае
А В В А

15. Пример

8 1
7 2
2 3
3 1 2
2 0
4
5 6 1

16. Самостоятельно

17.

47 77 37
S P 26 44 20
101 161 81
17.01.2025
17

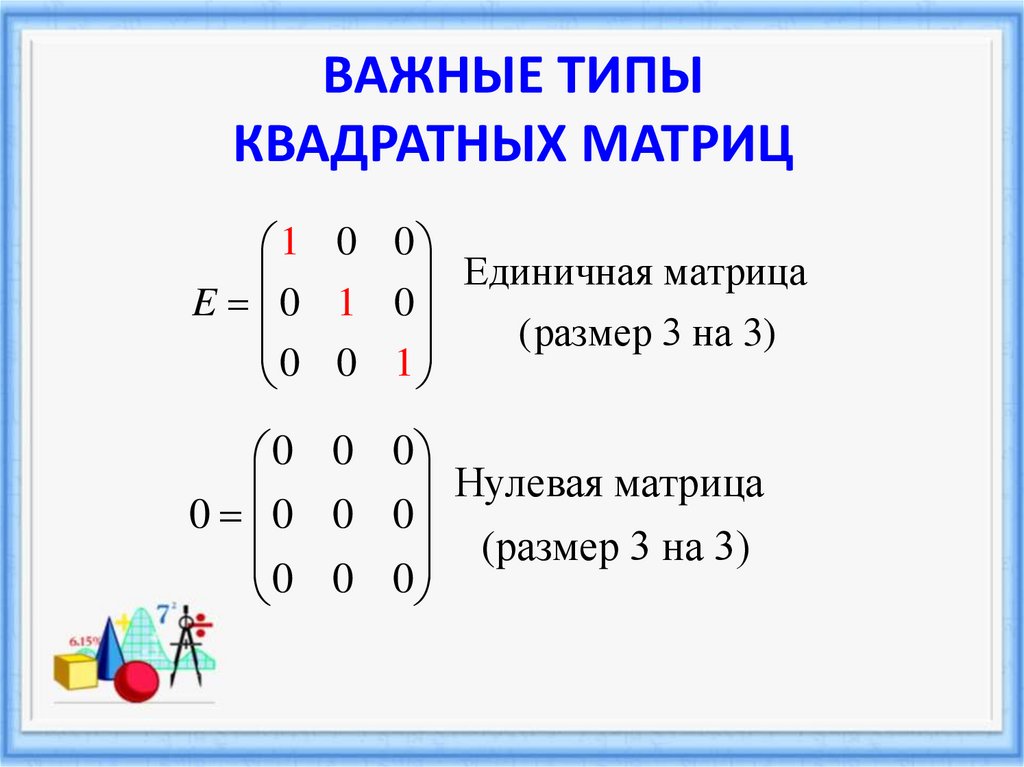
18. ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ

1 0 0
Единичная матрица
E 0 1 0
(размер 3 на 3)
0 0 1
0 0 0
Нулевая матрица
0 0 0 0
(размер 3 на 3)
0 0 0

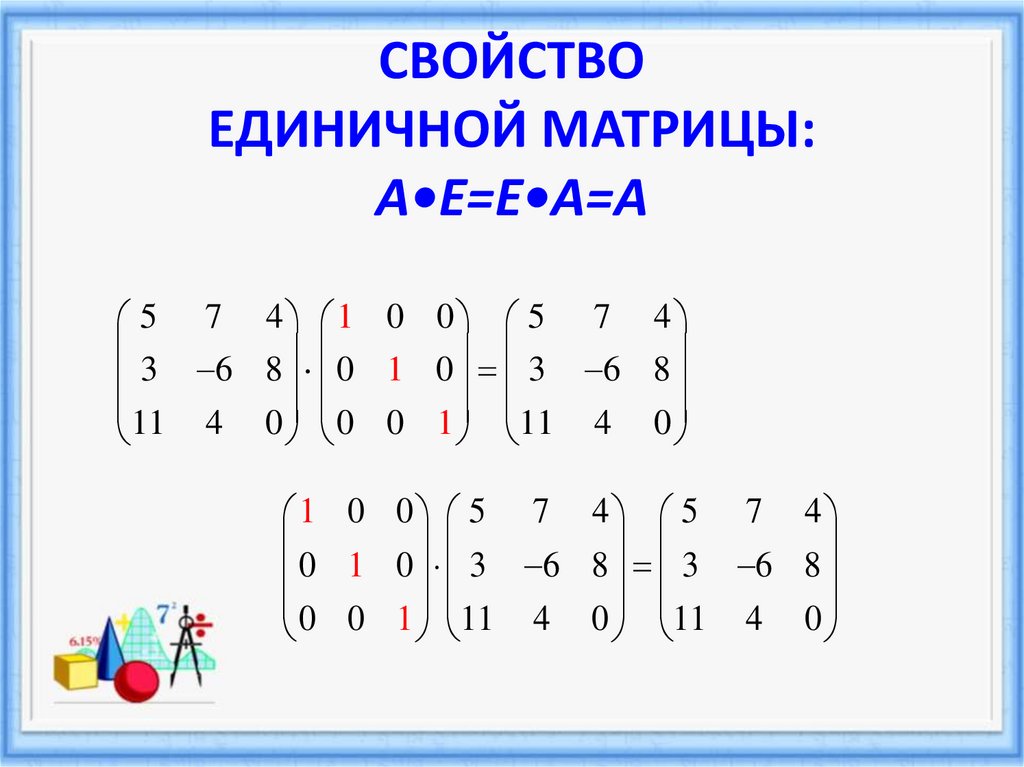
19. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A

5 7 4 1 0 0 5 7 4
3 6 8 0 1 0 3 6 8
11 4 0 0 0 1 11 4 0
1 0 0 5 7 4 5 7 4
0 1 0 3 6 8 3 6 8
0 0 1 11 4 0 11 4 0

20. Выполнение операций

Пример 2.
2 0
1
1 2 1
, В 1 3 0
А
3 1 0
1
4
1
Вычислить: 3В АT АТ
17.01.2025
20

21. Решить самостоятельно

1.
2.

22. Ответ:

1.
2.

23. Практическое задание

Вычислить:
1. D A 2 B
Ответ:
T
2. A A 3B
T
T
3. B B D C A
T
4. C A 4 D
5. A D 3 C
4 6
1.
7
18
1 18
2. AT A 3 BT
12 8
T
D A 2 B
3.
T
4.
T
5.
17.01.2025
129 56
0 17
16 2
T
C A 4 D 5 20
16
5
T
B B D C A
18 1 22
T
A D 3 C 9 12 36
10
4
0
23