Similar presentations:
Производная элементарных и сложных функций
1.
1Степенная
функция
14.01.2025
Тригонометрическая
функция
Логарифмическая
функция
Показательная
функция
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
2.
214.01.2025
14.01.2025
Производные некоторых
элементарных функций
Цель урока: Познакомиться с формулами
нахождения производных элементарных
функций и научиться их применять при
выполнении упражнений.
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
3.
3Новый материал
• Производные этих функций вычисляются по
формулам:
е е
х
х
1
ln x , х 0
х
• Найдем производную функции
ln a x
sin x cos x ;
cos x sin x
f( x) а
х
х ln a
а е
е
x
x
x ln a
х
x ln a
ln a а а ln a
а e
ln a e
14.01.2025
х
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
4.
4Новый материал
• Найдем производную функции
f ( x ) loga x
ln x
loga x
ln a
1
1 1
1
ln x
loga x
ln x
ln a
ln a x
x ln a
ln a
Из формулы производной сложной функции следует
формула:
14.01.2025
f ( kx b ) kf kx b
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
5.
5Таблица производных
f ( x ) kx b
f ( x )
f(x)
x
p
c
c - const
е
х
х
k
px
p 1
0
е
sin x
cos x
tgx
ctgx
ах
ln x
loga x
1
1
, x 0 х ln a , x 0
а ln a
х
х
14.01.2025
f ( x ) cos x sin x
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
6.
6Правила дифференцирования
f ( x ) u v
с u
c - const
14.01.2025
f ( x ) u v с u
u v
u v u v
u
v
u v u v
v2
1
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
7.
7Правила дифференцирования
f ( x ) u v
с u
c - const
14.01.2025
f ( x ) u v с u
u v
u v u v
u
v
u v f kx b
u v u v
v2
u v kf kx b
2
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
8.
8Правила дифференцирования
f ( x ) u v
с u
c - const
14.01.2025
f ( x ) u v с u
u v
u v u v
u
v
u v f kx b
u v u v
v2
u v kf kx b
3
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
9.
Сложная функция.Производная сложной
функции.
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
10.
10Рассмотрим функции
f t sin t
g x x 2 x 5
2
y sin x 2 2 x 5
y f g x
14.01.2025
Внешняя
функция
Внутренняя
функция
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
11.
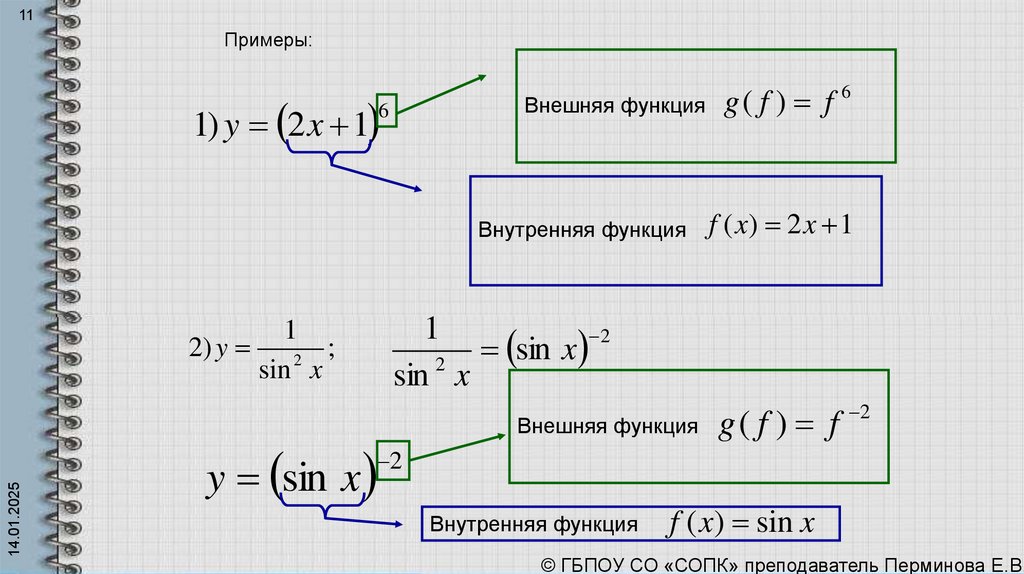
11Примеры:
1) y 2 x 1
Внешняя функция
6
Внутренняя функция
g( f ) f 6
f ( x) 2 x 1
1
2
sin x
2
sin x
1
2) y
;
2
sin x
y sin x
Внешняя функция
g ( f ) f 2
14.01.2025
2
Внутренняя функция
f ( x) sin x
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
12.
123) y tg 2 x
4
14.01.2025
Внешняя функция
Внутренняя функция
f ( x) 2 x
4
g ( f ) tgf
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
13.
13Определить внутреннюю и внешнюю функции для данной сложной
функции:
1) y 4 x 1
4
f ( x) 4 x 1 - внутренняя функция
14.01.2025
g( f ) f
4
- внешняя функция
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
14.
14Определить внутреннюю и внешнюю функцию для данной сложной
функции:
2) y sin 2 x
f ( x) 2 x - Внутренняя функция
14.01.2025
g ( f ) sin f
- Внешняя функция
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
15.
15Определить внутреннюю и внешнюю функцию для данной сложной
функции:
1
3) y
3
x 1
y x 1
3
f ( x) x 1 - Внутренняя функция
14.01.2025
g( f ) f
3
- Внешняя функция
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
16.
16Определить внутреннюю и внешнюю функцию для данной сложной
функции:
4) y cos x
2
y cos x
2
f ( x) cos x - Внутренняя функция
14.01.2025
g( f ) f
2 - Внешняя функция
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
17.
17h΄(x) = g´(f) • f ´(x)
Алгоритм нахождения производной
сложной функции
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f ´(x)
3)
Найди производную внешней функции g´(f)
14.01.2025
4)
Перемножь производные внутренней и внешней
функции и получишь производную сложной
функции
h΄(x) = f ´(x) • g´(f)
2
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
18.
18Алгоритм нахождения производной
сложной функции
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f ´(x)
3)
Найди производную внешней функции g´(f)
4) Перемножь производные внутренней и
внешней функции и получишь производную
h΄(x) = f ´(x) • g´(f)
сложной функции
а e ln a e
14.01.2025
х
x ln a
x ln a
1. f ( x) x ln a
g( f ) e f
'
'
f
(
x
)
(
x
ln
a
)
ln a
2.
3. g ' ( f ) ( e f ) ' e f
'
'
f
f
(
x
)
g
(
f
)
ln
a
e
4.
ln a а x а x ln a
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
19.
19Новый материал
Из формул kx b k и производной сложной функции
h ( x) f ( x) g ( f ) следует формула :
14.01.2025
f ( kx b )
kf kx b
3
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
20.
20Правило нахождения производной сложной функции
Алгоритм нахождения
производной сложной функции
1) y cos 4 x
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f ´(x)
3)
Найди производную внешней функции g´(f)
4)
Перемножь производные внутренней и
внешней функции и получишь производную
сложной функции h΄(x) = f ´(x) • g´(f)
14.01.2025
f ( x) 4 x
'
y
f
g
g
(
f
)
cos
f
y cos f 4 x sin f 4 4 sin f
4 sin 4 x
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
21.
21Алгоритм нахождения
производной сложной функции
2) y ctg 2 x
3
f ( x) 2 x
3
g ( f ) ctgf
y f g
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f ´(x)
3)
Найди производную внешней функции g´(f)
4)
'
Перемножь производные внутренней и
внешней функции и получишь производную
сложной функции h΄(x) = f ´(x) • g´(f)
1
2
y ctgf 2 x 2 2 2
3
sin f
sin f
2
sin 2 x
3
14.01.2025
2
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
22.
223) y sin x
2
f ( x) sin x
2
g ( f ) f
y sin x
2
Алгоритм нахождения
производной сложной функции
y f g '
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f ´(x)
3)
Найди производную внешней функции g´(f)
4)
sin x 2 f cos x
y f
2
Перемножь производные внутренней и
внешней функции и получишь производную
сложной функции h΄(x) = f ´(x) • g´(f)
14.01.2025
2 sin x cos x sin 2x
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
23.
234) y x 2 х
2
4
t x 2 х
y
f
t
f t 4
4
2
3
3
y t x 2 х 4t 2 x 2 8t x 1
2
14.01.2025
8 х 1 x 2 х
2
3
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
24.
24Найти производные функций:
1) y 8 1 4 x
1) y 1 4 x
3
1
2) y
2) y
2
3
x
2
3x 2
3) y 3 sin 3 x
3) y cos 3 x
4
4) y ctg 4 x 3 4) y 2
2
14.01.2025
sin 4 x 3
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
25.
25y 0
Решить уравнение
1) y cos 2 x x 1
y cos 2 x x 1 cos 2 x x 1
t 2 x
f cos t
cos t 2 x 1 0 sin t 2 1
14.01.2025
2 sin t 1 2 sin 2 x 1
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
26.
262 sin 2x 1 0
2 sin 2x 1
2 sin 2x 1
sin t a
1
sin 2 x
2
t 1 arcsin a k , k Z
k
1
2 x 1 arcsin k
2
k
k
k
,k Z
2 x 1 k , x 1
12 2
6
14.01.2025
k
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
27.
272) y sin 4 x 2 x 3
y 0
y sin 4 x 2 x 3 sin 4 x 2 x 3
t 4 x
f sin t
sin t 4 x 2 0 cos t 4 2 4 cos t 2
14.01.2025
4 cos 4x 2
4 cos 4x 2 0
1
cos 4 x
2
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
28.
281
cos 4 x
2
cos t a
t arccos a 2 n, n Z
1
4 x arccos 2 n,
2
14.01.2025
4x
3
2 n
x
12
n
2
,n Z
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
29.
29x x
3) y sin
2 4
y 0
x x
x x
y sin sin
2 4
2 4
x
x 1
t ,
sin t x
2
2 4
f sin t
14.01.2025
1 1 1
1
cos t cos t
2 4 2
4
1
x 1
cos
2
2 4
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.
30.
301
x 1
cos 0
2
2 4
1
x
1
cos
2
2
4
x
1
cos
2
2
x
1
arccos 2 n
2
2
14.01.2025
x
2
2 n
2
3
4
x
4 n, n Z
3
© ГБПОУ СО «СОПК» преподаватель Перминова Е.В.





















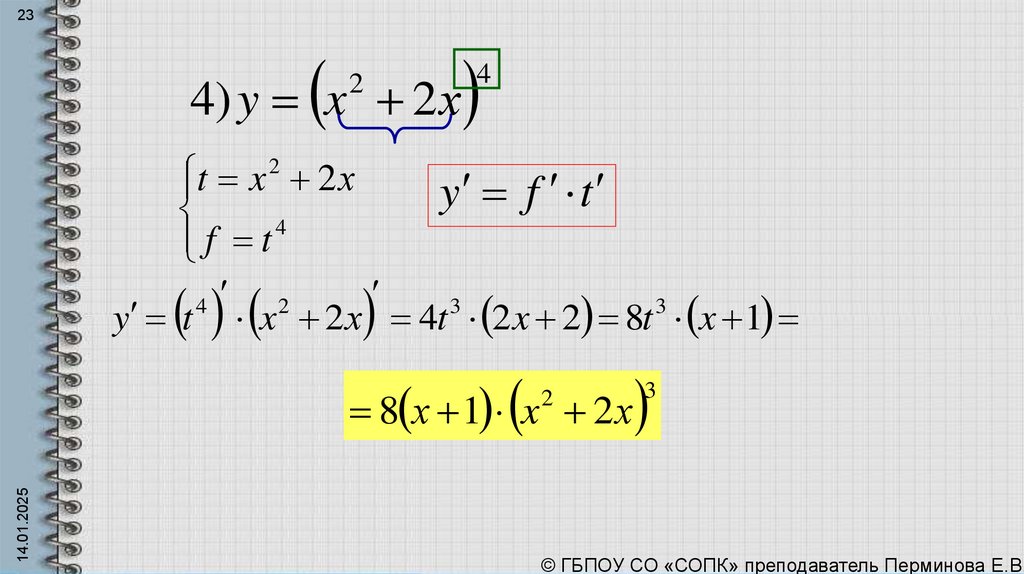



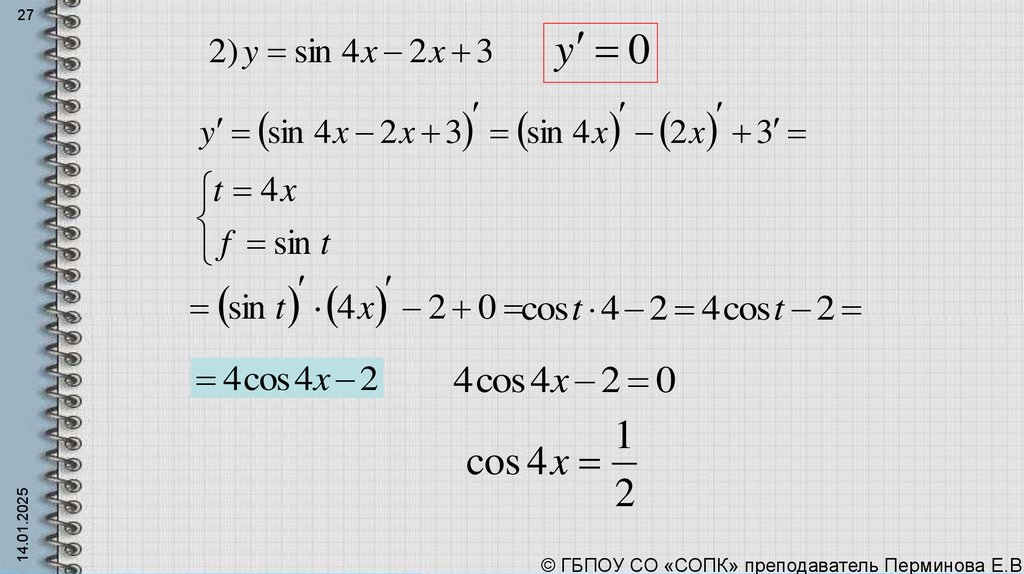



 mathematics
mathematics








