Способы преобразования комплексного чертежа

1.

Лекция 5
СПОСОБЫ
ПРЕОБРАЗОВАНИЯ
КОМПЛЕКСНОГО
ЧЕРТЕЖА
Красовская Н.И.

2.

Основные положения

3.

При ортогональном
проецировании «удобное»
положение геометрического
объекта достигается
двумя путями:

4.

1. Перемещением плоскостей проекций
в новое положение, по отношению к которому
проецируемый геометрический объект окажется в
частном положении
(объект неподвижен)
2. Перемещением геометрического объекта так,
чтобы он занял частное положение относительно
заданных плоскостей проекций, которые при этом не
меняют своего положения в пространстве
(объект подвижен)

5.

Способы приведения
геометрического объекта в
«удобное» положение для решения
метрических и позиционных задач
называются
способами преобразования
комплексного чертежа

6.

Способ замены
плоскостей проекций

7.

Изменение взаимного положения геометрического
объекта и плоскостей проекций достигается
введением
дополнительной плоскости проекций
Плоскость вводится
перпендикулярно
к одной из заданных плоскостей проекций,
чтобы по отношению к ней проецируемый объект
занял частное положение

8.

Алгоритмы решения задач
способом замены
плоскостей проекций

9.

Задача
Заданы две проекции точки.
Построить новую проекцию точки на
дополнительную плоскость проекций

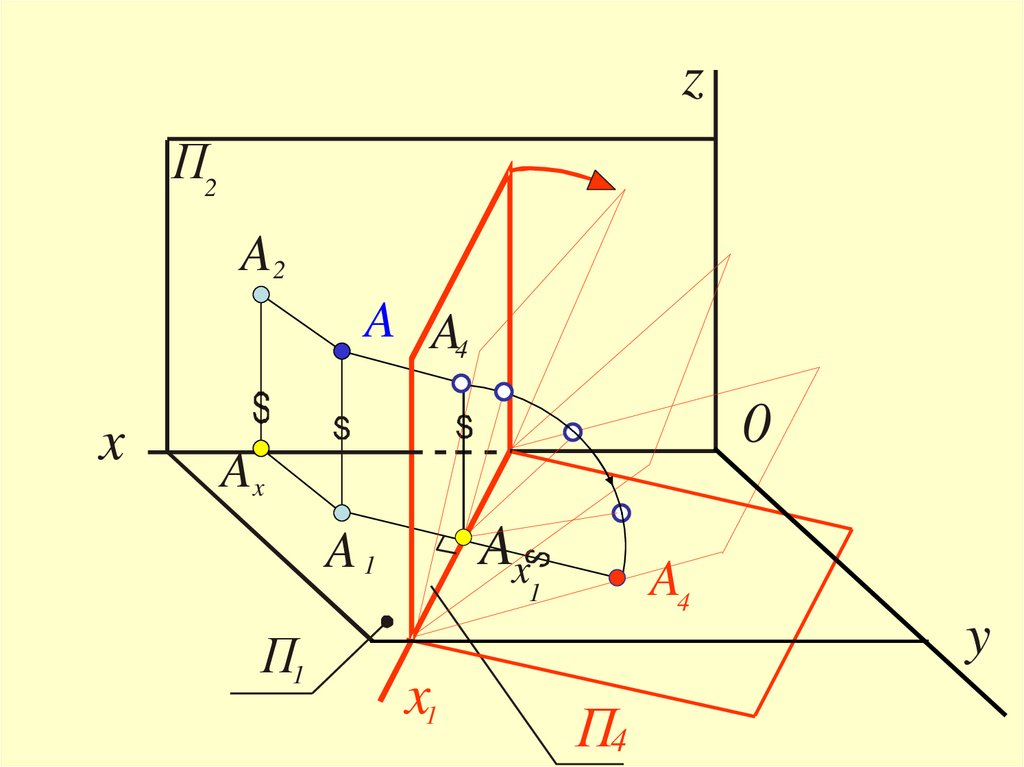
10.

z
П2
A2
A A4
x
0
Ax
Ax
A1
A4
1
П1
x1
П4
y

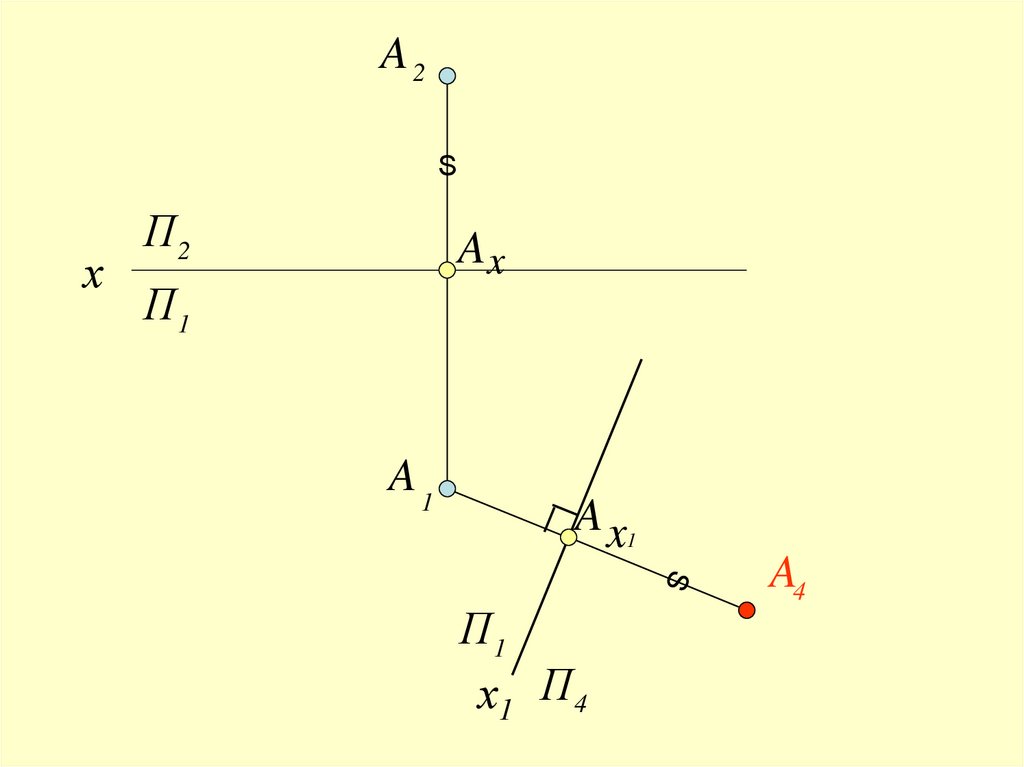
11.

A2
S
х
П2
Ax
П1
A1
A x1
П1
х1 П 4
A4

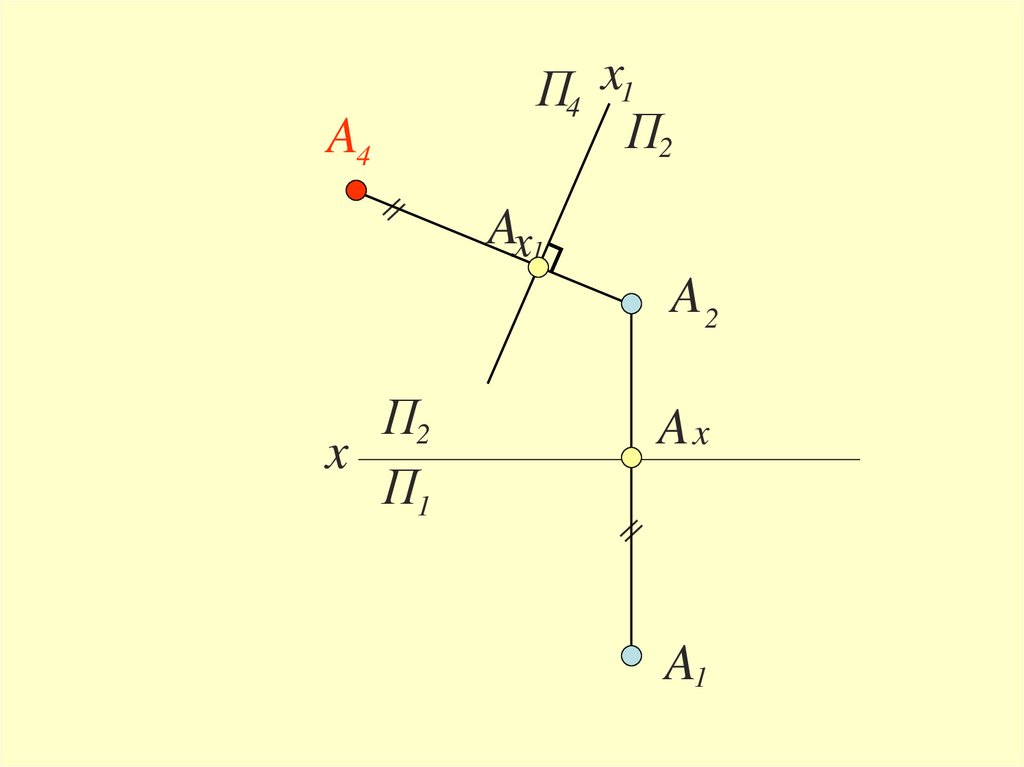
12.

A4
П4 x1
П2
Ax1
A2
П2
x
П1
Ax
A1

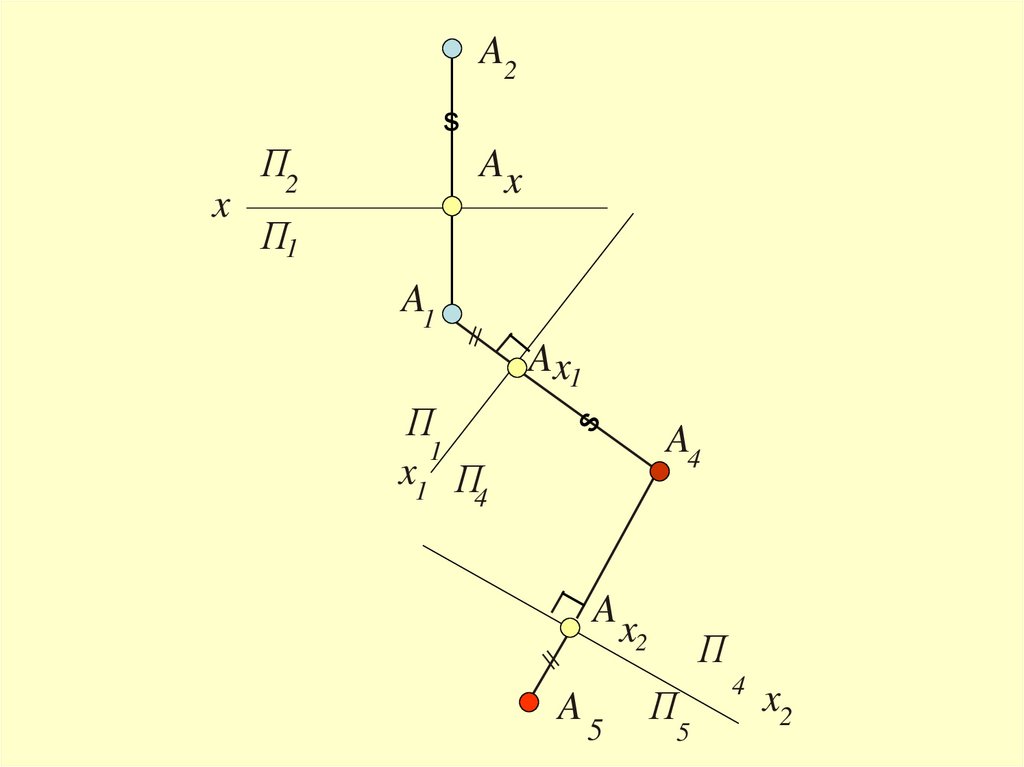
13.

При нескольких заменах плоскостей
проекций каждую последующую ось
обозначают x2, х3, х4
и т.д.,
а каждую новую плоскость проекций –
П5, П6 , П7
и т.д.

14.

A2
s
x
П2
Ax
П1
A1
Ax1
П
1
x1 П
A4
4
Ax
П
2
A
5
П
5
4
x2

15.

Решение четырёх основных
задач преобразования
комплексного чертежа
способом замены
плоскостей проекций

16.

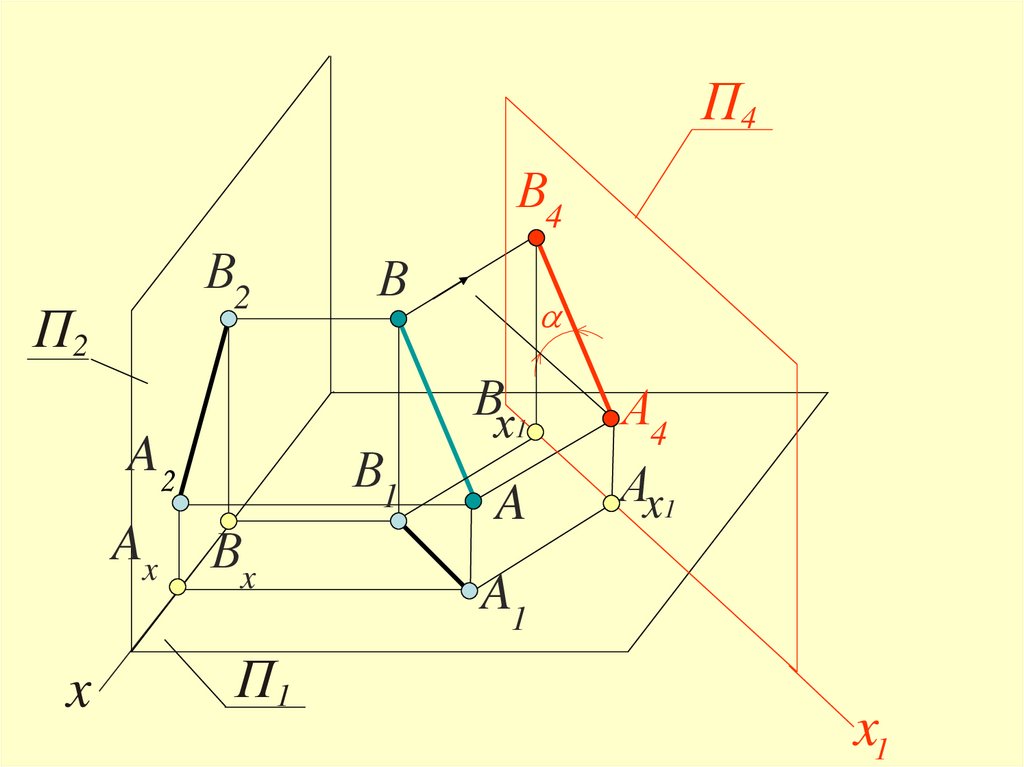
Задача 1
Преобразовать чертёж так, чтобы в новой
системе плоскостей проекций
прямая общего положения
заняла положение
прямой уровня

17.

П4
В4
В2
П2
A2
Ax
x
В
В1
Вx
П1
a
Вх1
A
А4
Аx1
A1
x1

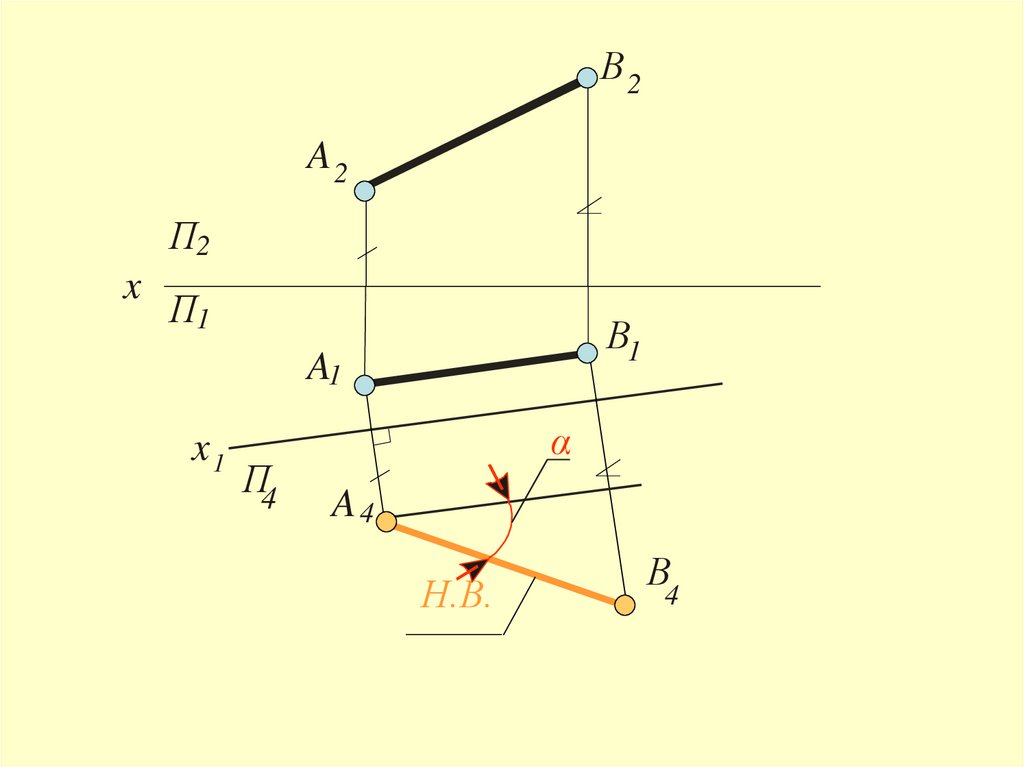
18.

В2
A2
П2
x
П1
В1
A1
x1
П4
α
A4
Н.В.
В4

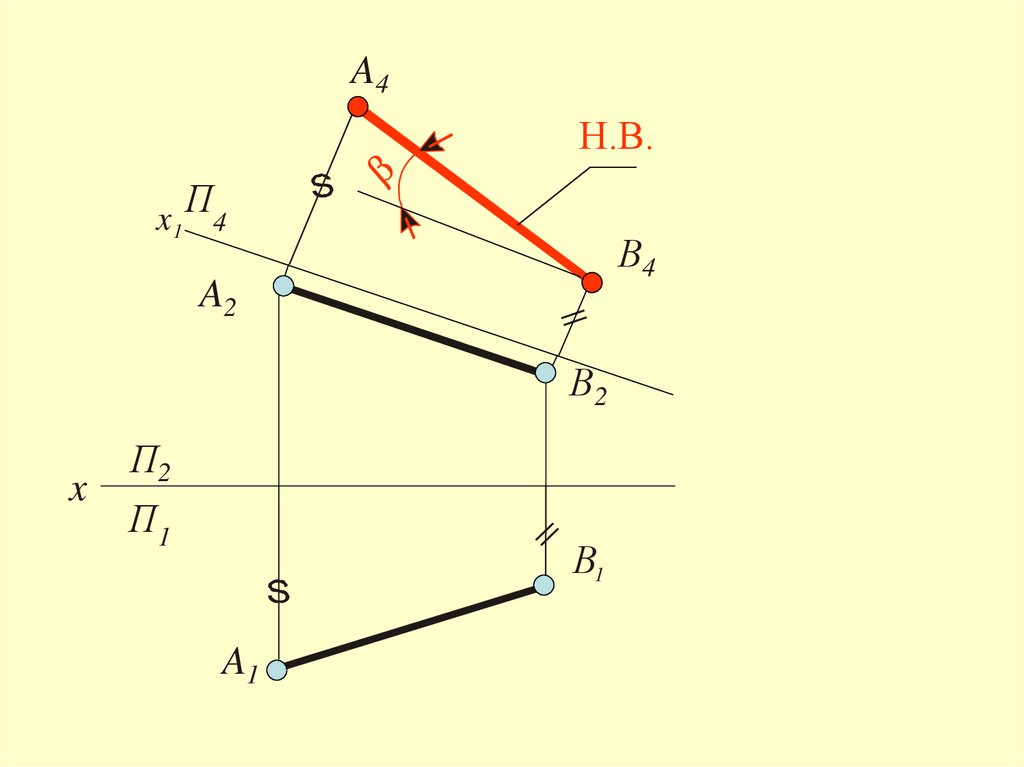
19.

A4
Н.В.
x1
П4
В4
A2
В2
x
П2
П1
В1
A1

20.

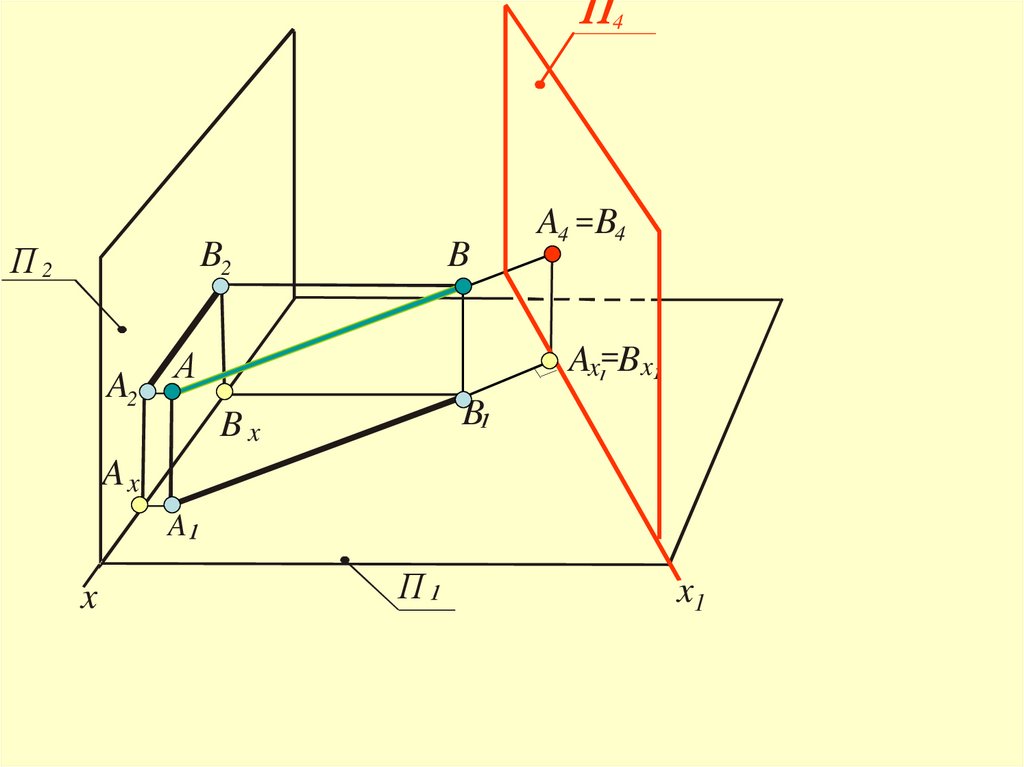
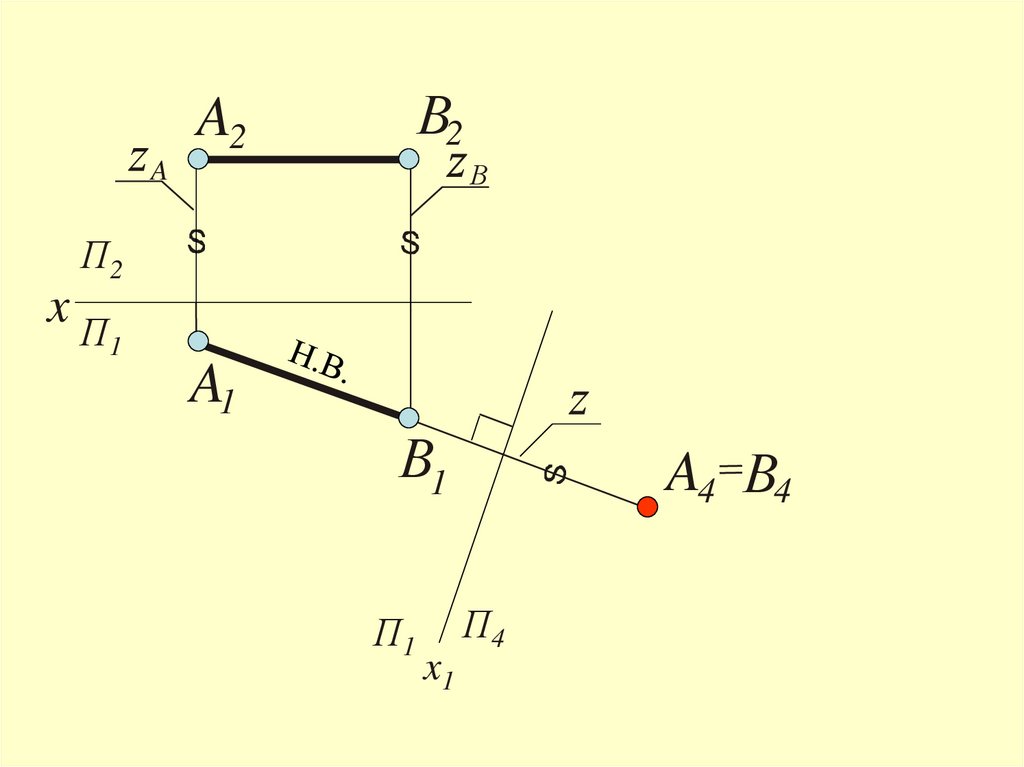
Задача 2
Преобразовать чертёж так, чтобы в
новой системе плоскостей проекций
прямая уровня
заняла положение
проецирующей прямой

21.

4
П2
B2
A2
B
A4 = B4
Ax =Bx
А
B
Bx
Ax
A
x
П
x1

22.

В2
A2
В
A
П2
xП
1
A1
В1
П1
x1
A4 В4
П4

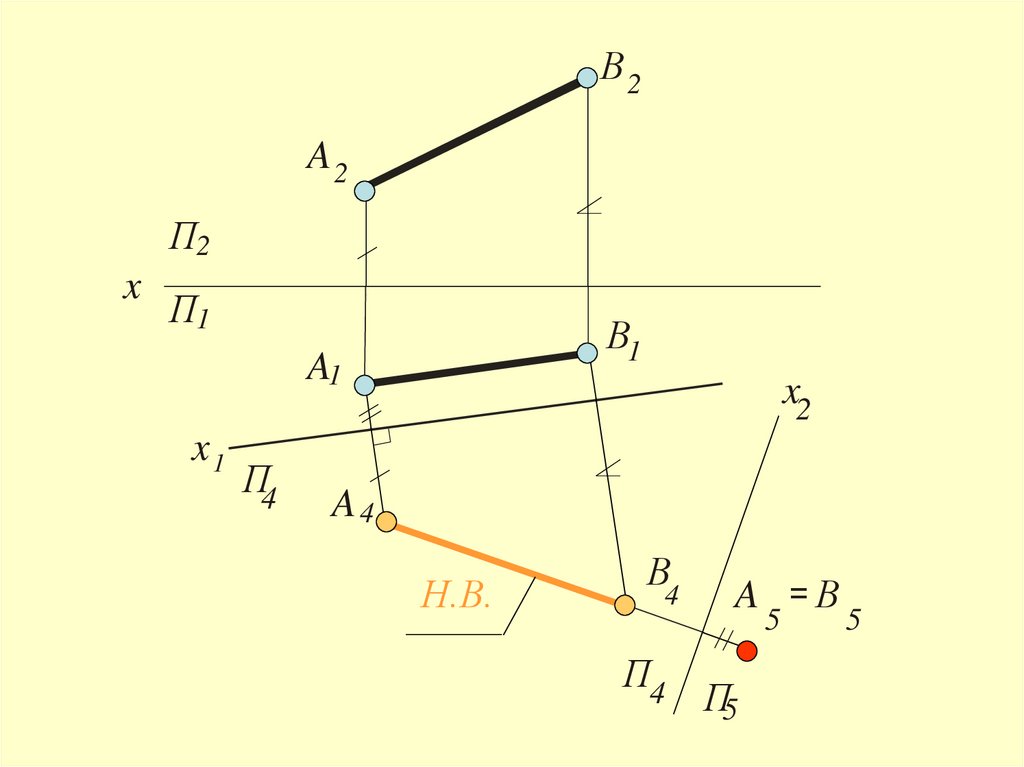
23.

Для преобразования
прямой общего положения в проецирующую
необходимо решить
последовательно первую и вторую
задачи преобразования чертежа

24.

В2
A2
П2
x
П1
В1
A1
x1
П4
x2
A4
Н.В.
В4
П4
A =В
5
П5
5

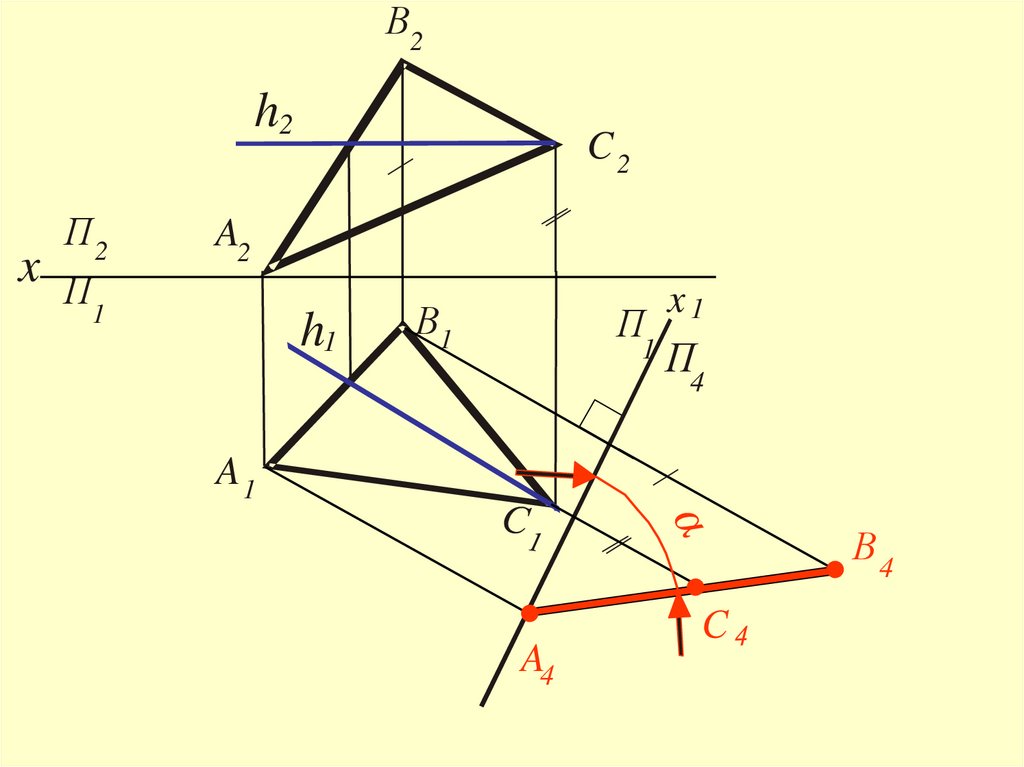
25.

Задача 3
Преобразовать чертёж так,
чтобы в новой системе плоскостей проекций
плоскость общего положения
заняла
проецирующее
положение

26.

Новая плоскость П4 должна быть
перпендикулярна
какой-нибудь прямой, лежащей в
заданной плоскости - (АВС)
Как следует из теоремы о проекциях прямого угла,
эта прямая должна быть прямой уровня

27.

В2
h2
П2
x П
1
C2
A2
h1
В1
П
x1
1П
4
A1
В4
A4

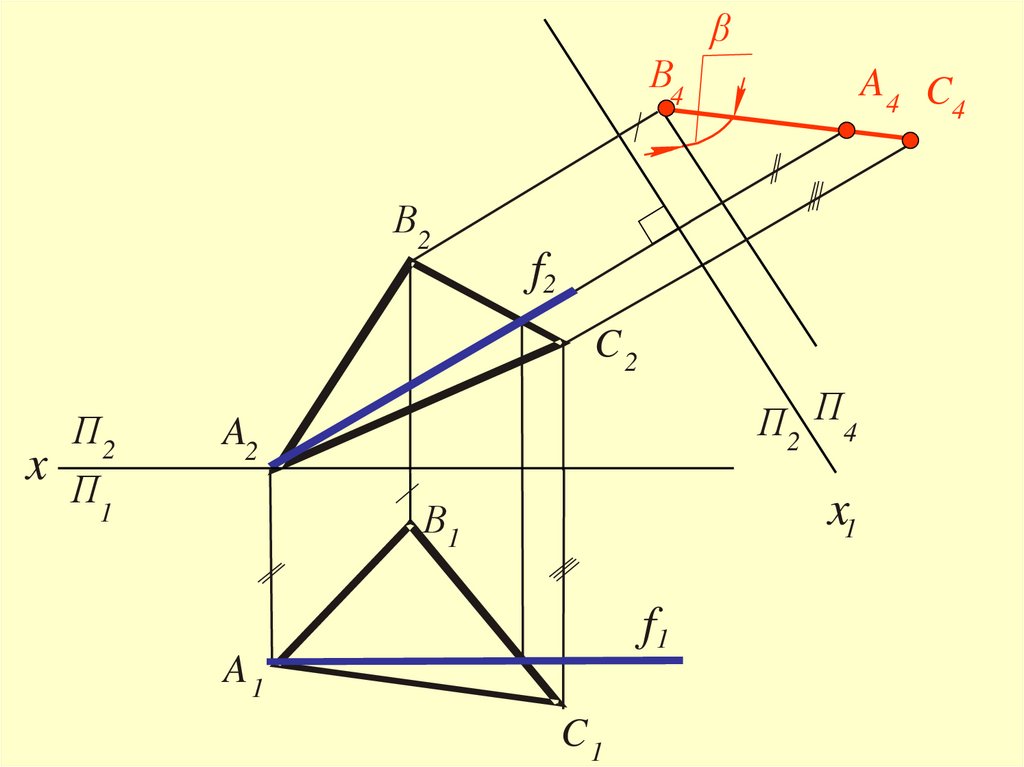
28.

β
В4
В2
A4 C
f2
C2
П2
x П
1
П2 П 4
A2
x1
В1
f1
A1
C1
4

29.

Задача 4
Преобразовать чертёж так,
чтобы в новой системе плоскостей проекций
плоскость проецирующая
заняла положение
плоскости уровня

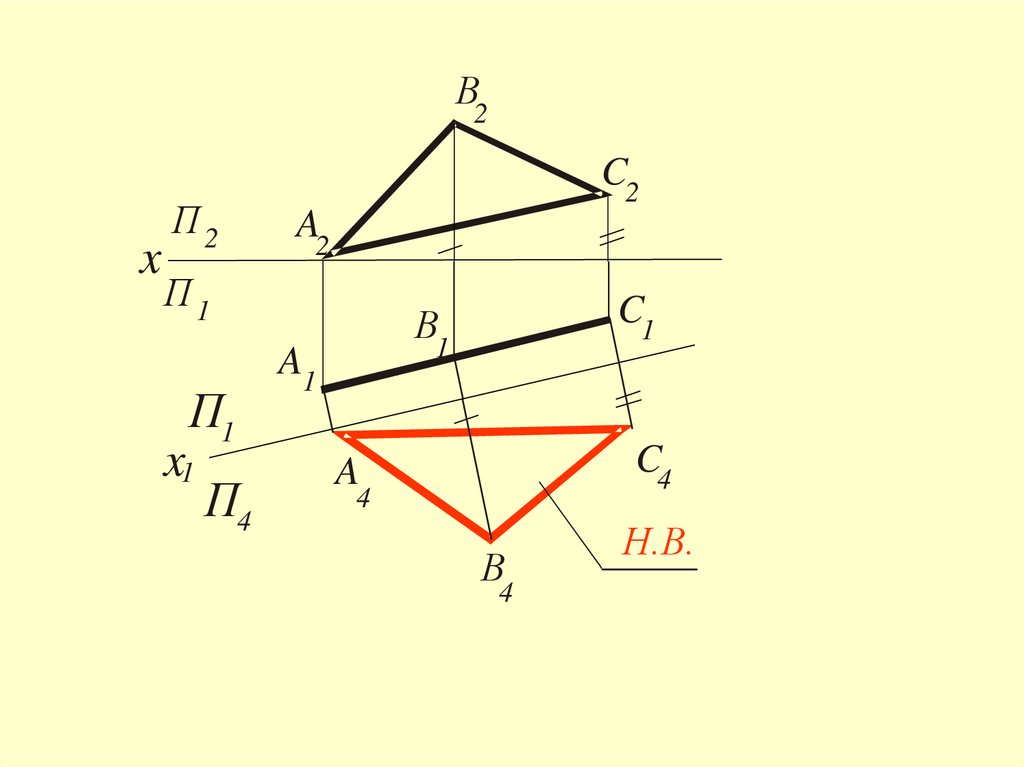
30.

В2
x
П2
C2
A2
П1
П1
x1
П4
C1
В1
A1
C4
A
4
В
4
Н.В.

31.

Чтобы плоскость общего положения
преобразовать в плоскость уровня,
надо решить последовательно
3и4
задачи преобразования

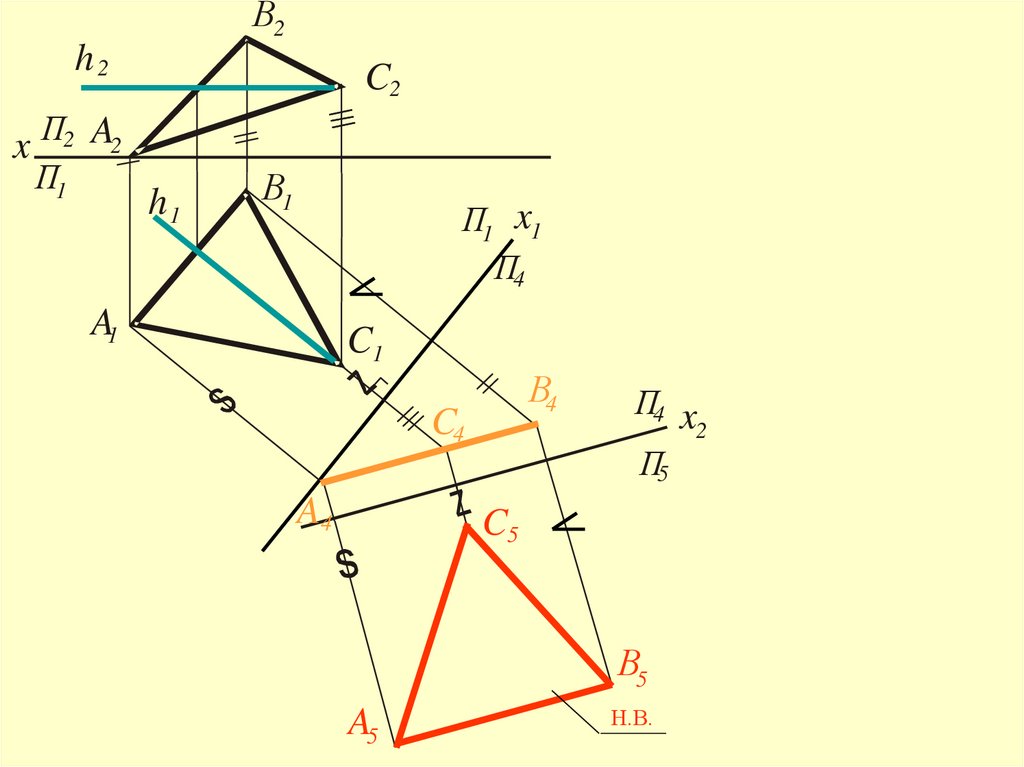
32.

В2
h2
П2 A2
x
П1
C2
h1
В1
П1 x1
П4
A1
C1
В4
C4
A4
П4 x
2
П5
C5
В5
A5
Н.В.

33.

Способ плоскопараллельного
перемещения

34.

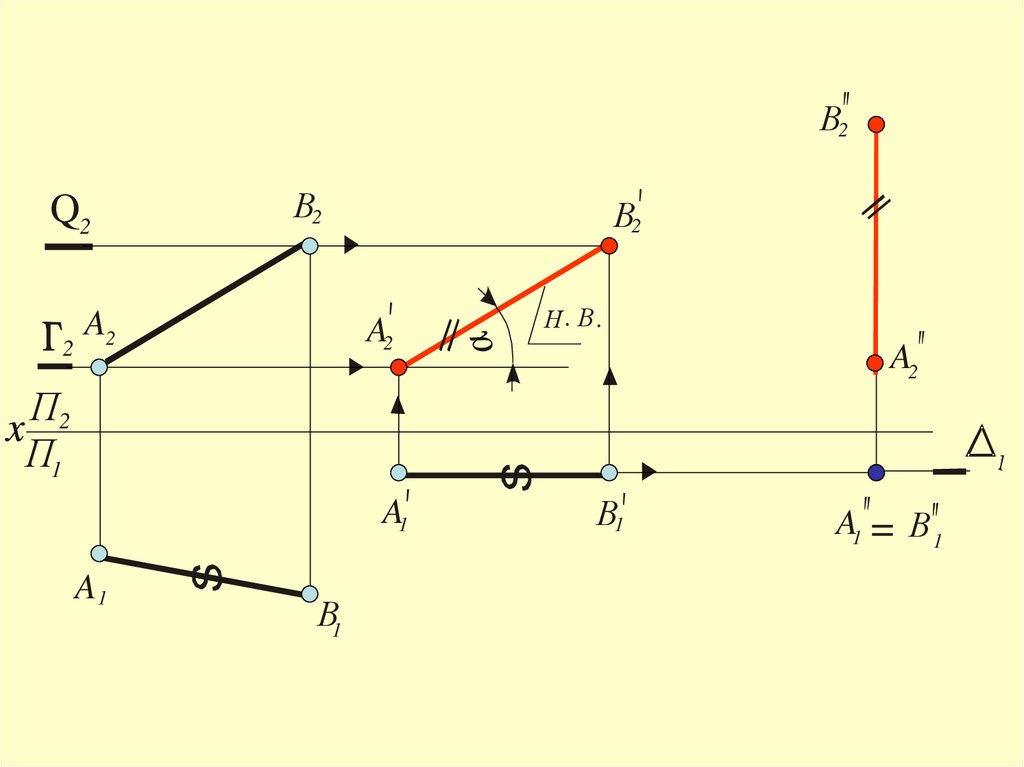
Решение первой и второй задач
преобразования чертежа
способом плоскопараллельного
перемещения

35.

В2
Q2
2
В2
A2
В2
A2
Н. В.
A2
П
x 2
П1
A1
A1
В1
В1
A1 = В 1

36.

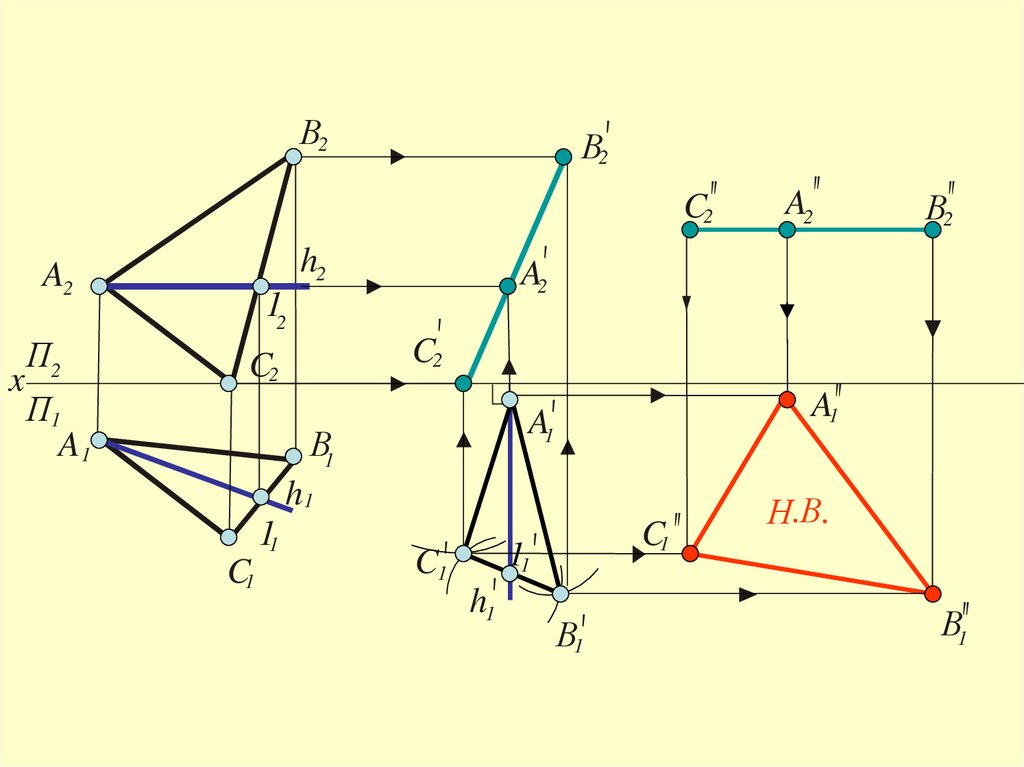
Решение третьей и четвёртой задач
преобразования
чертежа способом
плоскопараллельного перемещения

37.

В2
В2
C2
h2
A2
x
П2
C2
C2
A1
A1
В1
h1
11
C1
В2
A2
12
П1
A1
A2
C1
11
C1
h1
В1
Н.В.
В1

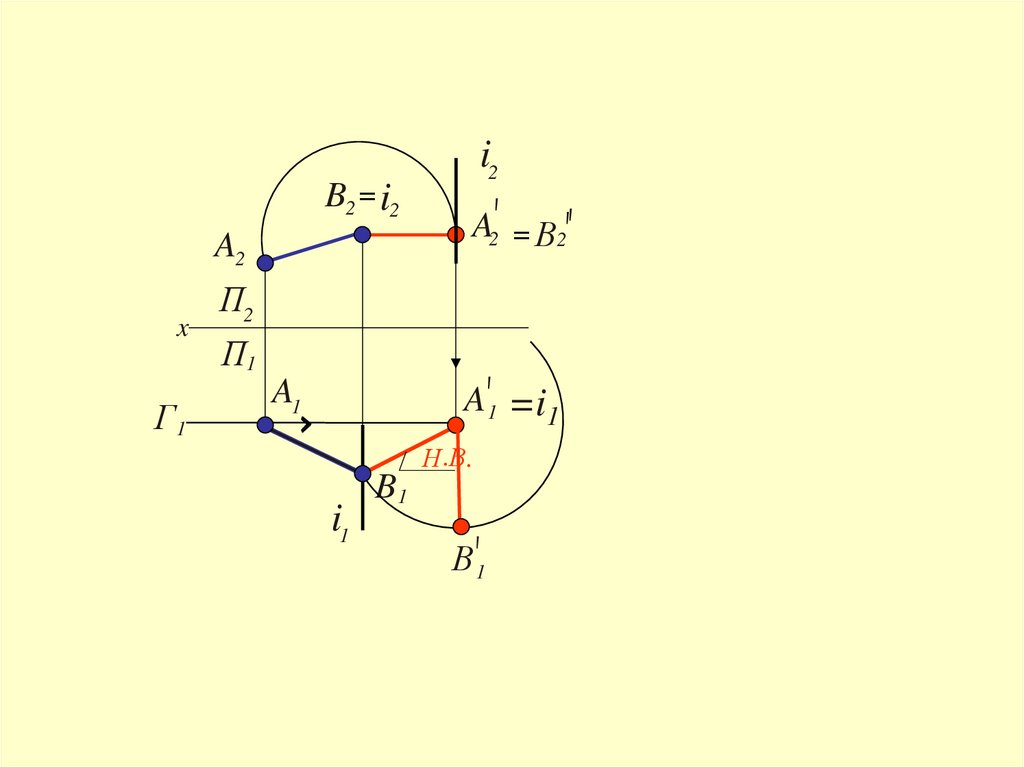
38.

B2= i2
A2
x
Г1
i2
A2 = В2
П2
П1
A1
A 1 =i1
Н. В.
i1
B1
В1

39.

Лекция 6
Алгоритмы решения
типовых метрических задач
начертательной геометрии
способом замены плоскостей
проекций
Красовская Н.И.

40.

Метрические задачи связаны с определением
метрических величин геометрических объектов,
т.е. их длин, площадей, периметров и т.п.,
а также расстояний и углов между объектами
Для удобства все метрические задачи можно
разделить на два основных типа:
определение расстояний
определение углов

41.

Определение расстояний

42.

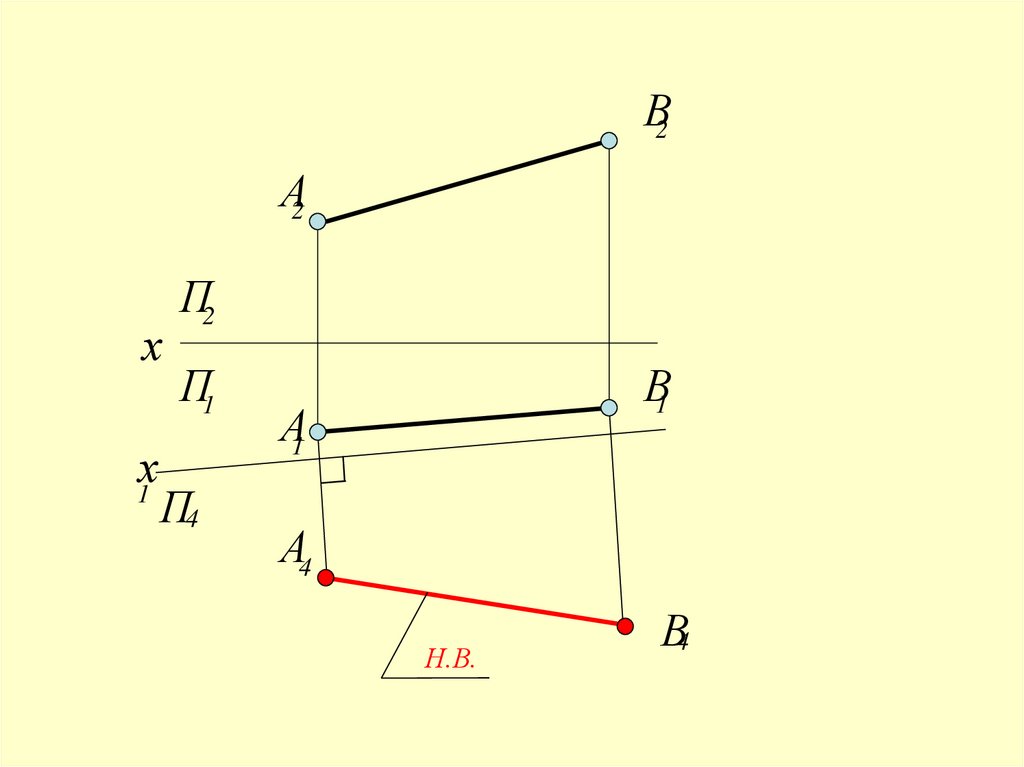
Для решения задачи необходимо прямую
общего положения
преобразовать
в прямую уровня
(1-ая задача преобразования чертежа)

43.

В2
А2
х
х1
П2
П1
П4
В1
А1
А4
Н.В.
В4

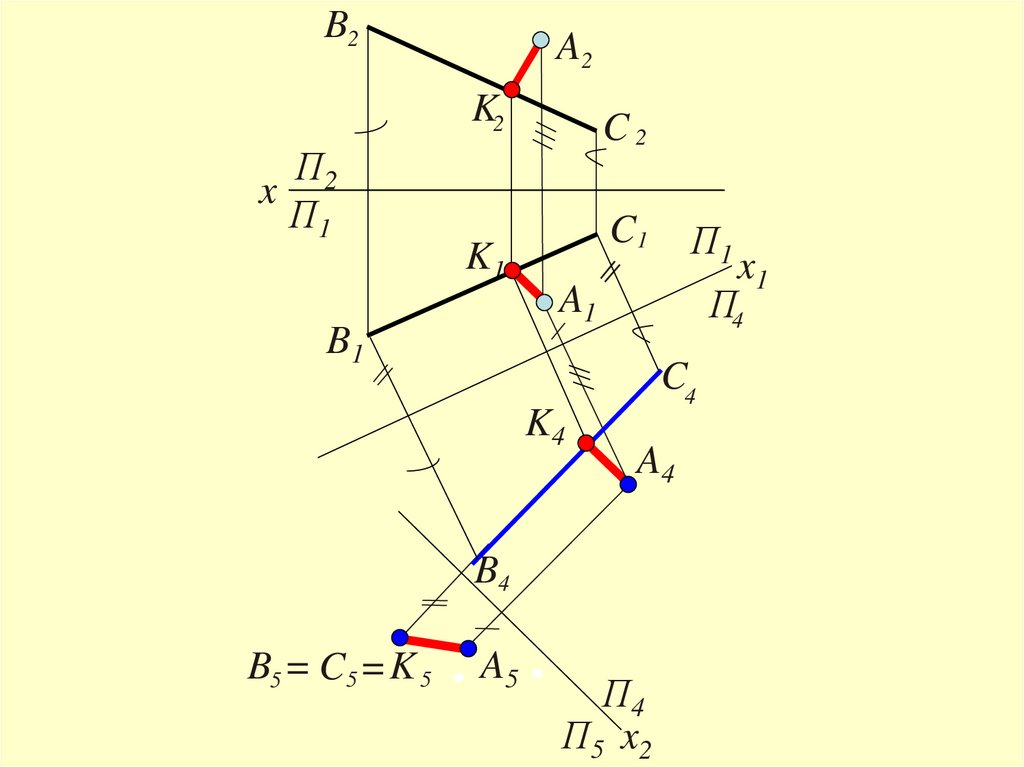
44.

Расстояние между точкой и
заданной прямой
определяется
величиной отрезка перпендикуляра,
опущенного из точки на прямую

45.

B2
A2
K2
П2
x
П1
K1
B1
C2
C1
C4
A4
B4
A5
x1
П4
A1
K4
B5 = C5 = K 5
П1
П4
П5 x2

46.

Для решения задачи необходимо прямую
общего положения преобразовать в
проецирующую прямую
(1-ая и 2-ая
задачи преобразования чертежа)

47.

Расстояние между двумя
параллельными прямыми.
Определяется величиной отрезка
перпендикуляра, опущенного из точки,
взятой на одной прямой, на другую прямую

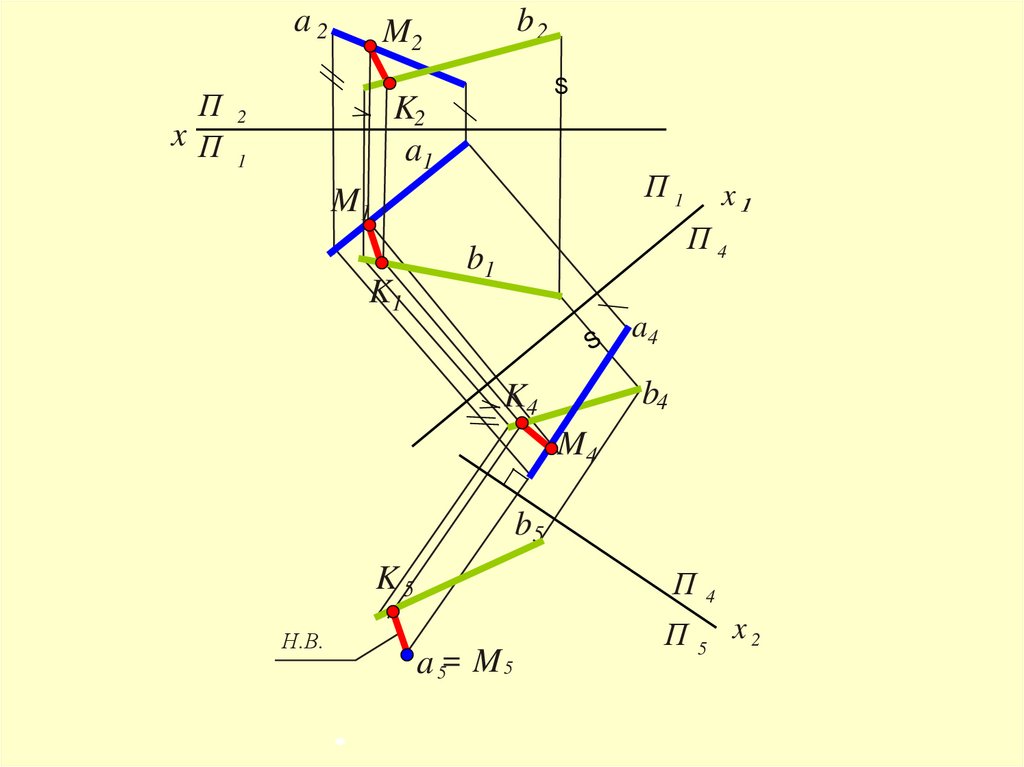
48.

Для решения задачи необходимо обе прямые
преобразовать в проецирующие
(1-ая и 2-ая
задачи преобразования чертежа)

49.

K2
П2
x
П
a2
b2
M2
K
a1
M
b1
M4
П
x П4
Графическое решение
возвращается в исходную
систему
b4
a
K4 4
b5 =M5
a5= K5
П4 П5
x2
Н.В.

50.

Расстояние между двумя
скрещивающимися прямыми
Определяется величиной перпендикуляра,
заключенного между параллельными
плоскостями, которым принадлежат
скрещивающиеся прямые

51.

Для решения задачи необходимо одну из
прямых преобразовать в проецирующую.
Затем из точки, в которую она спроецируется,
опустить перпендикуляр на вторую прямую
(1-ая и 2-ая
задачи преобразования чертежа)

52.

a2
b2
M2
П 2
xП
1
S
K2
a1
П1
M1
K1
x
П4
b1
a4
b4
K4
M4
b5
K5
Н.В.
П4
a 5= M 5
П 5 x2

53.

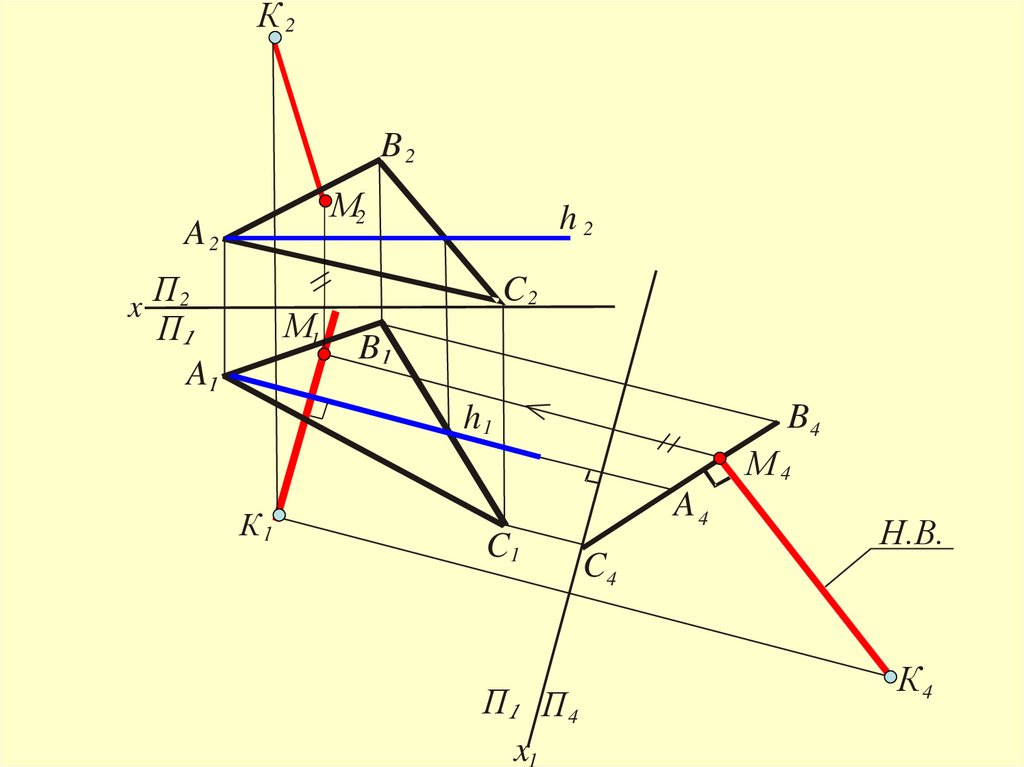
Расстояние от точки до заданной
плоскости
Определяется величиной отрезка
перпендикуляра, опущенного из точки на
плоскость.
Решение задачи сводится к нахождению расстояния
между этой точкой и ближайшей к ней точкой на
заданной плоскости

54.

Для решения задачи необходимо плоскость
общего положения преобразовать в
проецирующую.
Из точки К – (К4) опустить
перпендикуляр на эту плоскость
(3-я задача преобразования)

55.

К2
B2
М2
A2
x
П2
П
A
М1
h2
C2
B
B4
h1
М4
К
A4
C1
П П4
x1
Н.В.
C4
К4

56.

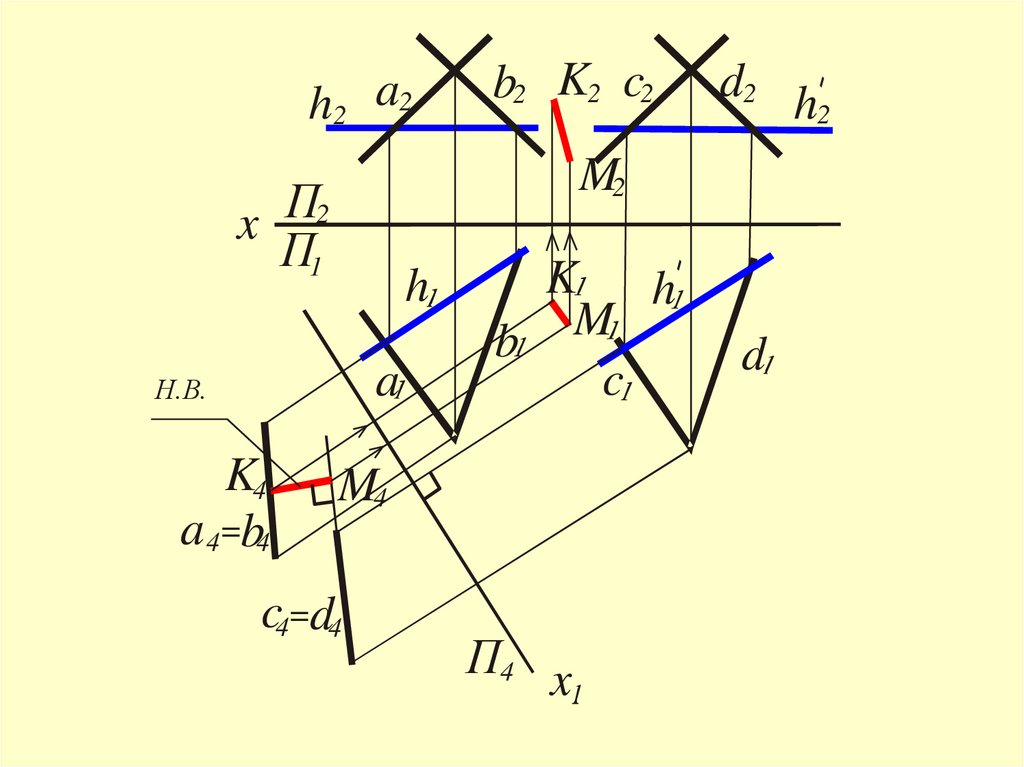
Расстояние между двумя
параллельными плоскостями
Измеряется величиной отрезка
перпендикуляра, опущенного из точки,
взятой на одной плоскости, на другую
плоскость

57.

Для решения задачи необходимо
обе плоскости преобразовать
в проецирующие
(3-я задача преобразования чертежа)

58.

h2 a2
d2 h
2
M2
П
x 2
П1
h
a
Н.В.
K4
a 4=b4
b2 K2 c2
K
h
M
b
c
M4
c4=d4
П4 x
d

59.

Определение углов

60.

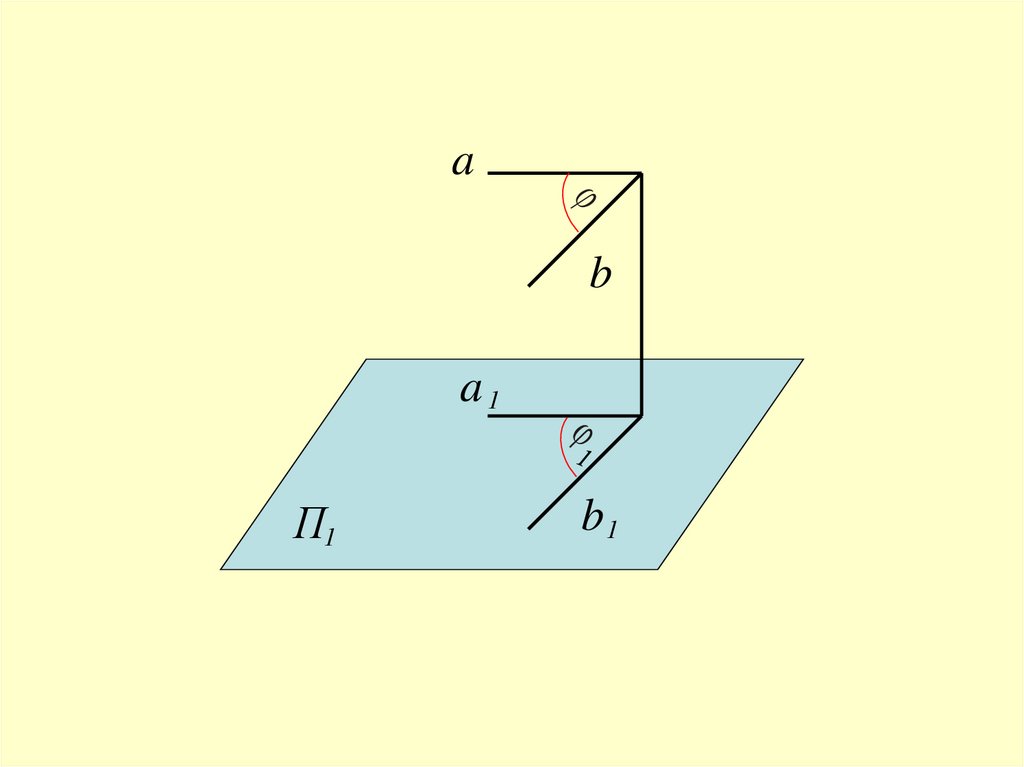
Угол между прямыми линиями
определяется как линейный угол,
плоскость которого должна занять
положение уровня.
(Решаются 3-я и 4-я задачи преобразования)

61.

a
b
b
a
a
=
b
a
a1
b
=
b1
П1
b

62.

Угол между кривыми линиями
измеряется углом
между их касательными

63.

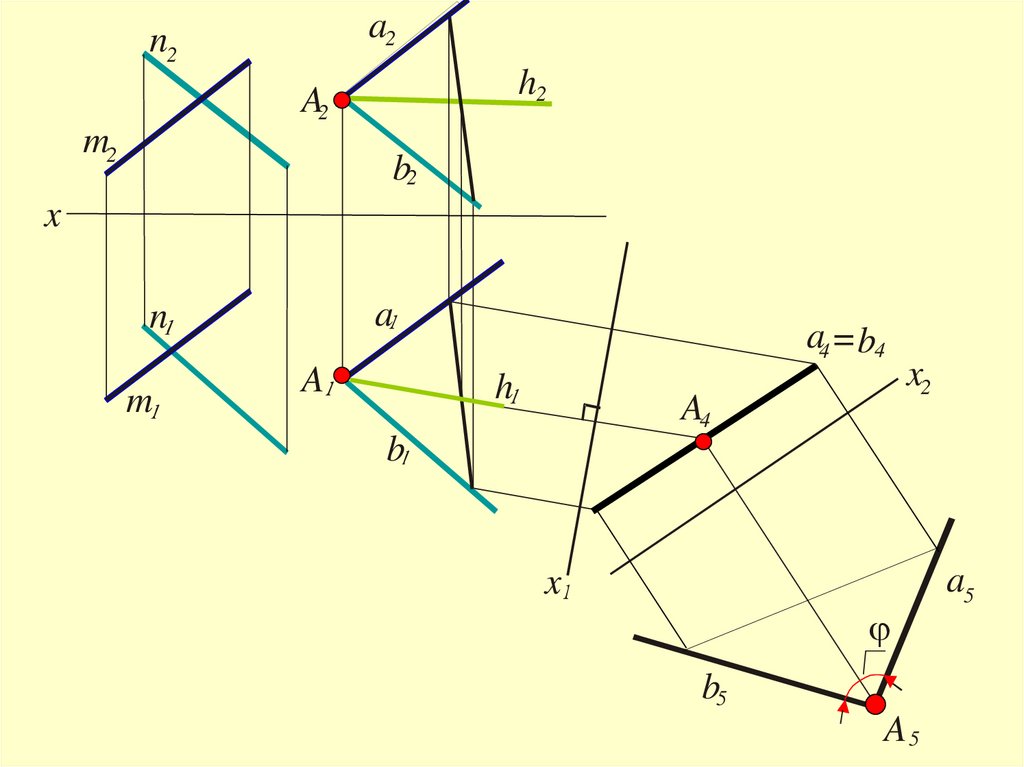
Угол между скрещивающимися
прямыми
измеряется плоским углом, образованным
пересекающимися прямыми, проведенными
из произвольной точки параллельно данным
скрещивающимся прямым
(Решаются 3-я и 4-я задачи преобразования)

64.

a2
n2
h2
A2
m2
b2
x
a
n
m
A
a4 = b4
h
A4
x2
b
x
b5
A5
a5

65.

Угол между прямой и плоскостью
измеряется острым углом между этой
прямой и ее проекцией на эту плоскость
(Угол проще определить, если определить
сначала дополняющий угол α)

66.

Угол между двумя плоскостями
(двугранный угол)
измеряется величиной своего линейного угла,
плоскость которого перпендикулярна
ребру двугранного угла

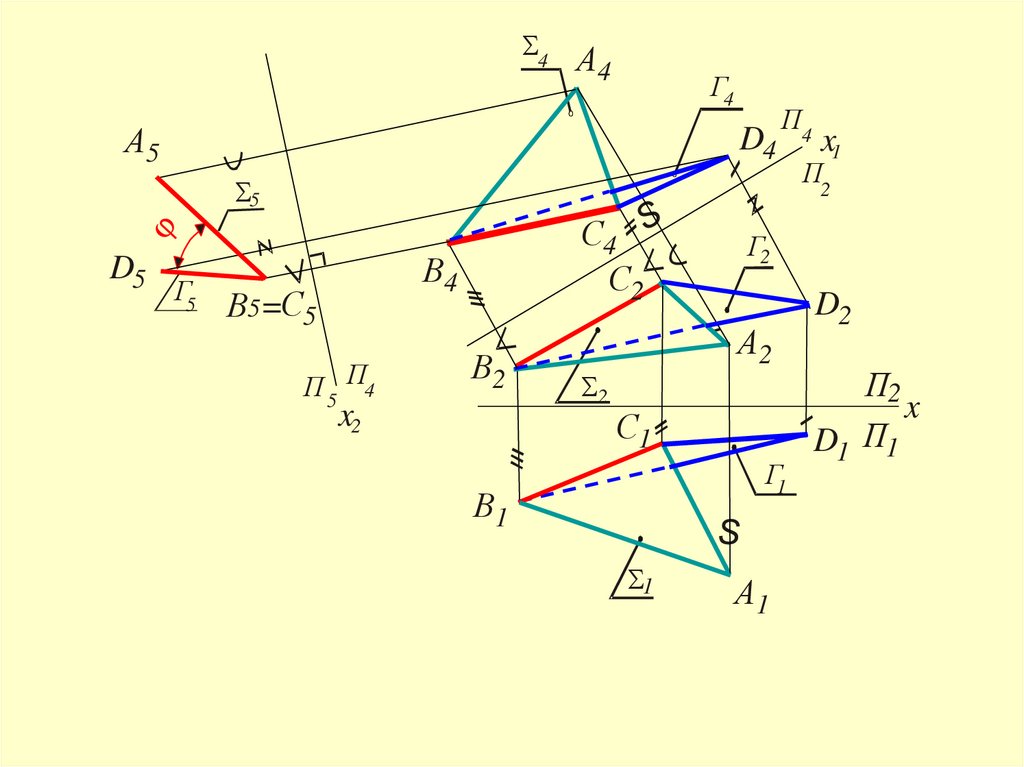
67.

Для решения задачи необходимо ребро
двугранного угла преобразовать в
проецирующее
(1-ая и 2-ая задачи преобразования чертежа)

68.

4
А4
Г4
А5
D4
П4
5
D5
Г5
С4
С2
В4
В5=С5
П 5 П4
В2
x2
2
С1
Г1
1
П2
Г2
А2
В1
x1
А1
D2
П2
x
D1 П1

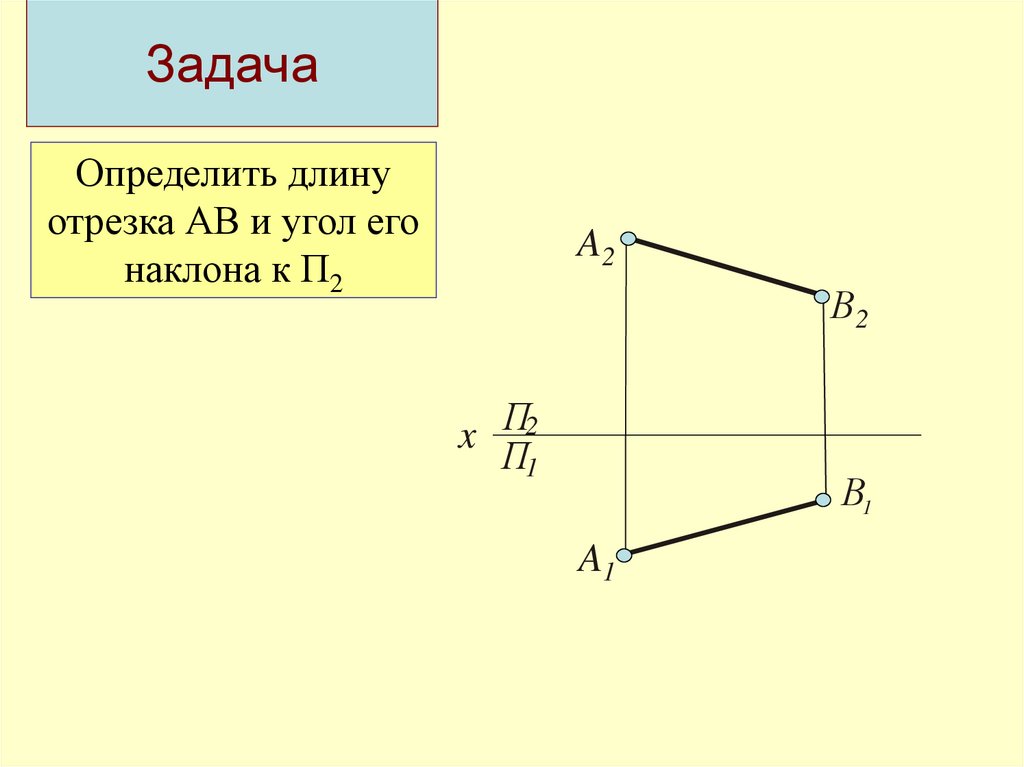
69. Задача

Определить длину
отрезка АВ и угол его
наклона к П2
A2
В2
x П2
П1
В1
A1

70.

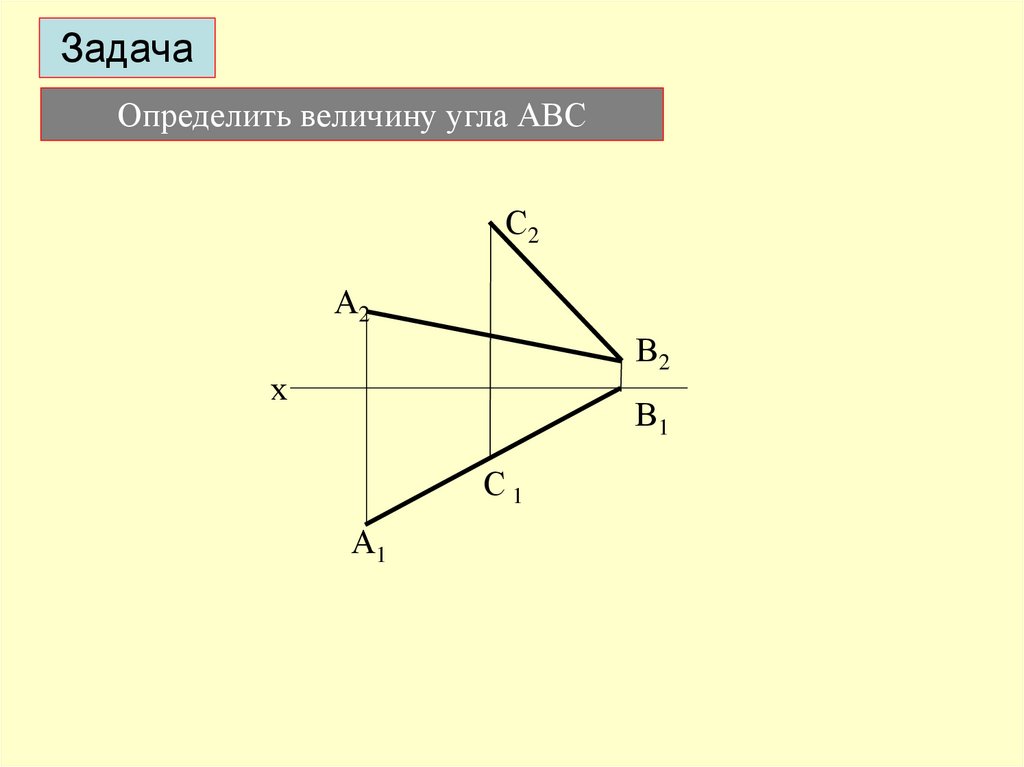
Задача
Определить величину угла АВС
С2
А2
В2
х
В1
С1
А1