Способы преобразования чертежа. Лекция 4

1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Лекция 4. Способы преобразования чертежа

Пьянкова Жанна Анатольевна,
доцент каф. «ПиЭА», канд. пед. наук
1

2. Основные способы преобразования

• Способ перемены (замены) плоскостей
проекций
• Способ плоскопараллельного
перемещения
• Способ вращения вокруг проецирующих
прямых
• Способ вращения вокруг линий уровня

3. ЧЕТЫРЕ ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ СПОСОБАМИ ПРЕОБРАЗОВАНИЯ

1.
ПРЕОБРАЗОВАТЬ ПРЯМУЮ ОБЩЕГО
ПОЛОЖЕНИЯ В ПРЯМУЮ ЧАСТНОГО
ПОЛОЖЕНИЯ (ГОРИЗОНТАЛЬ ИЛИ ФРОНТАЛЬ)
2.
ПРЕОБРАЗОВАТЬ ПРЯМУЮ ЧАСТНОГО
ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩУЮ ПРЯМУЮ
3.
ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ОБЩЕГО
ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩУЮ ПЛОСКОСТЬ
4. ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ
ПРОЕЦИРУЮЩУЮ В ПЛОСКОСТЬ УРОВНЯ

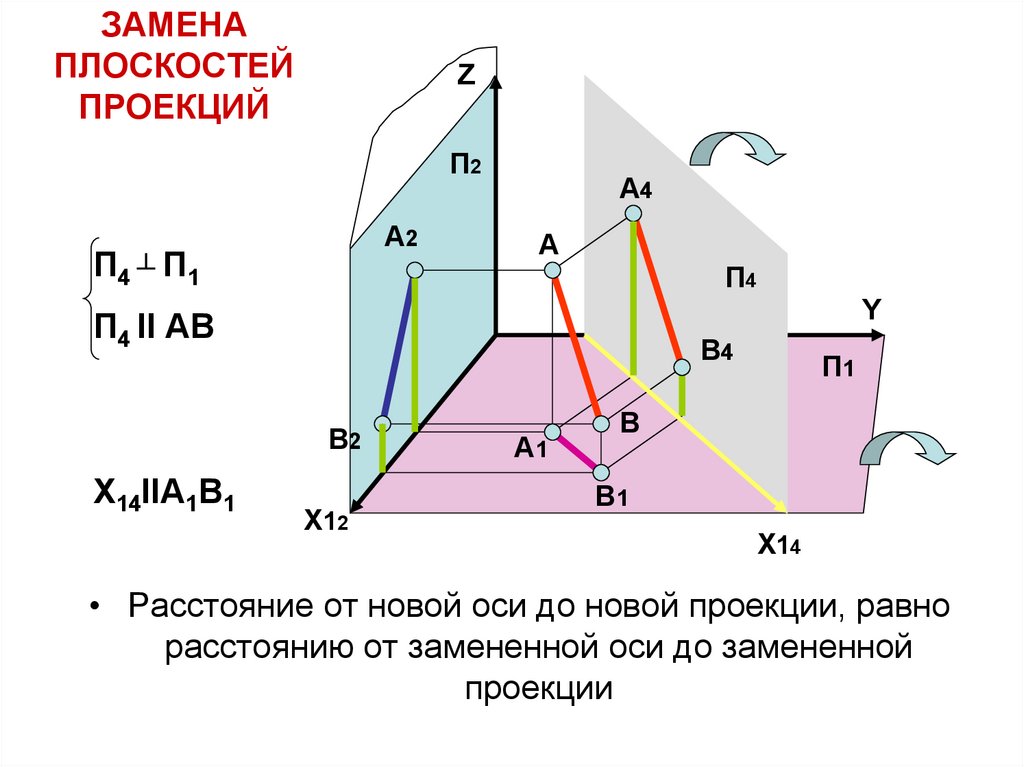
4. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Z
П2
А2
П4 ┴ П1
А4
А
П4
Y
П4 II АВ
В4
В2
X14IIA1B1
X12
А1
П1
В
В1
X14
• Расстояние от новой оси до новой проекции, равно
расстоянию от замененной оси до замененной
проекции

5. Позиционная задача

• Определить углы (φ и ψ)наклона
прямой к горизонтальной и
фронтальной плоскостям проекций,
если А(15,40,10); В(65,30,15).
• Задачу решить способом замены
плоскостей проекций

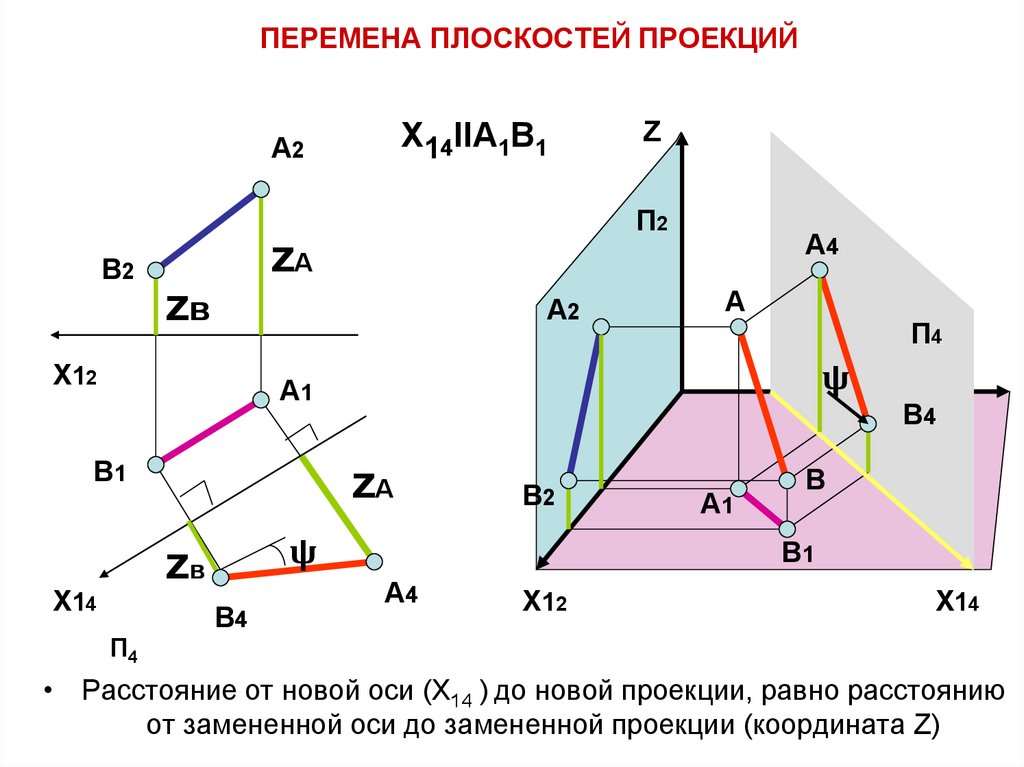
6. ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ

X14IIA1B1
А2
Z
П2
А4
zА
В2
zв
А2
X12
А
П4
ψ
А1
В1
zА
В2
ψ
zв
X14
В4
В4
А1
В
В1
А4
X12
X14
П4
• Расстояние от новой оси (X14 ) до новой проекции, равно расстоянию
от замененной оси до замененной проекции (координата Z)

7.

А5
• Для определения угла
наклона к фронтальной
φ
В5
плоскости проекций (φ) и
натуральной величины
отрезка установим
плоскость П5,
параллельную отрезку АВ.
• П5 ┴ П2
П5 II АВ
А2
ОX25
П5
П2
X12
В2
П1
А1
В1
ψ
П1
ОX14 П4
В4
А4
ОX25IIA2B2

8. Вывод:

• При замене плоскости проекций П2 на новую
плоскость П4 положение новой
прямоугольной проекции точки определяется
ее аппликатой (координатой Z)
• При замене плоскости проекций П1 на новую
плоскость П5 положение новой
прямоугольной проекции точки определяется
ее ординатой (координатой Y)

9. Метрическая задача

• Определить натуральную величину
треугольника АВС и угол его
наклона к горизонтальной
плоскости проекций
• А(90,0,20); В(60,50,40); С(10,20,10)

10.

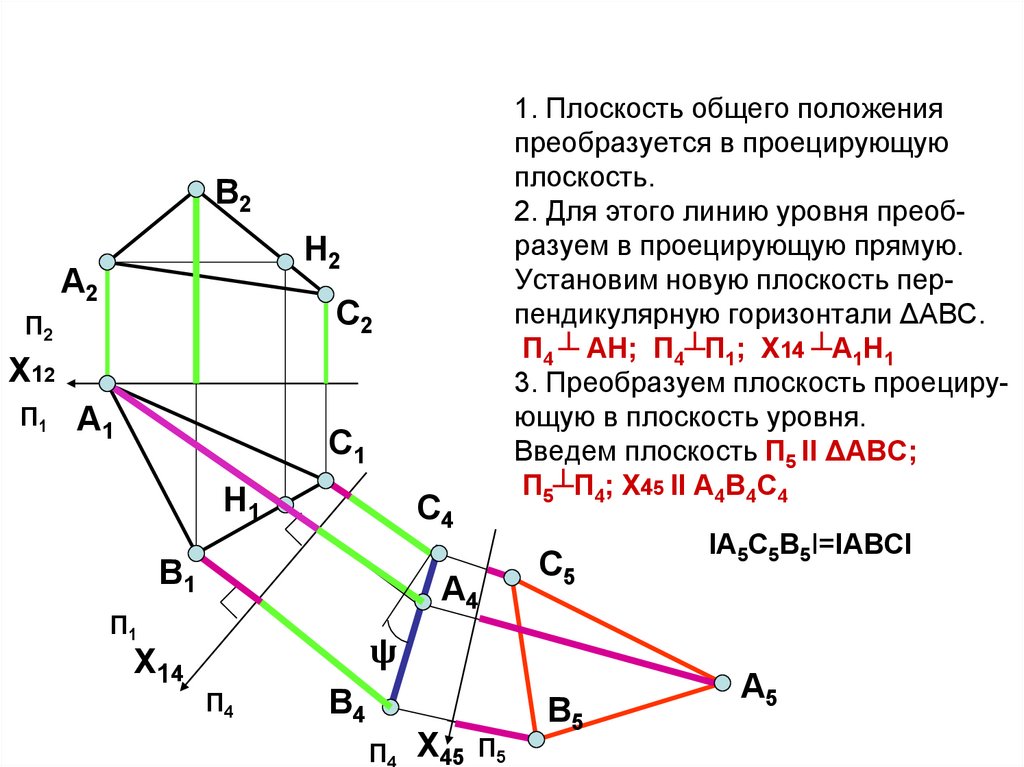
1. Плоскость общего положения
преобразуется в проецирующую
плоскость.
2. Для этого линию уровня преобразуем в проецирующую прямую.
Установим новую плоскость перпендикулярную горизонтали ΔАВС.
П4 ┴ АH; П4┴П1; X14 ┴A1H1
3. Преобразуем плоскость проецирующую в плоскость уровня.
Введем плоскость П5 ІІ ΔАВС;
П5┴П4; X45 II A4B4C4
B2
H2
A2
C2
П2
X12
П1
A1
C1
H1
C4
B1
A4
П1
X14
С5
ψ
П4
B4
П4
X45
П5
В5
ІА5С5В5І=ІАВСІ
А5

11. Сущность способа плоскопараллельного перемещения

• Заданный геометрический объект совершает
плоскопараллельное движение, при котором
ВСЕ ЕГО ТОЧКИ движутся параллельно
некоторой плоскости до положения
параллельного или перпендикулярного
плоскости проекций
• Линия, по которой происходит перемещение всех
точек объекта, находится В ПЛОСКОСТИ УРОВНЯ

12.

• Определить натуральную величину отрезка
прямой способом плоско-параллельного
перемещения
B2
IАВI
B 2’
A2
ψ
A 2’
X
A1
B1
A1’
B 1’
Горизонтальная проекция не меняет своей величины, но плоскопараллельно перемещается

13.

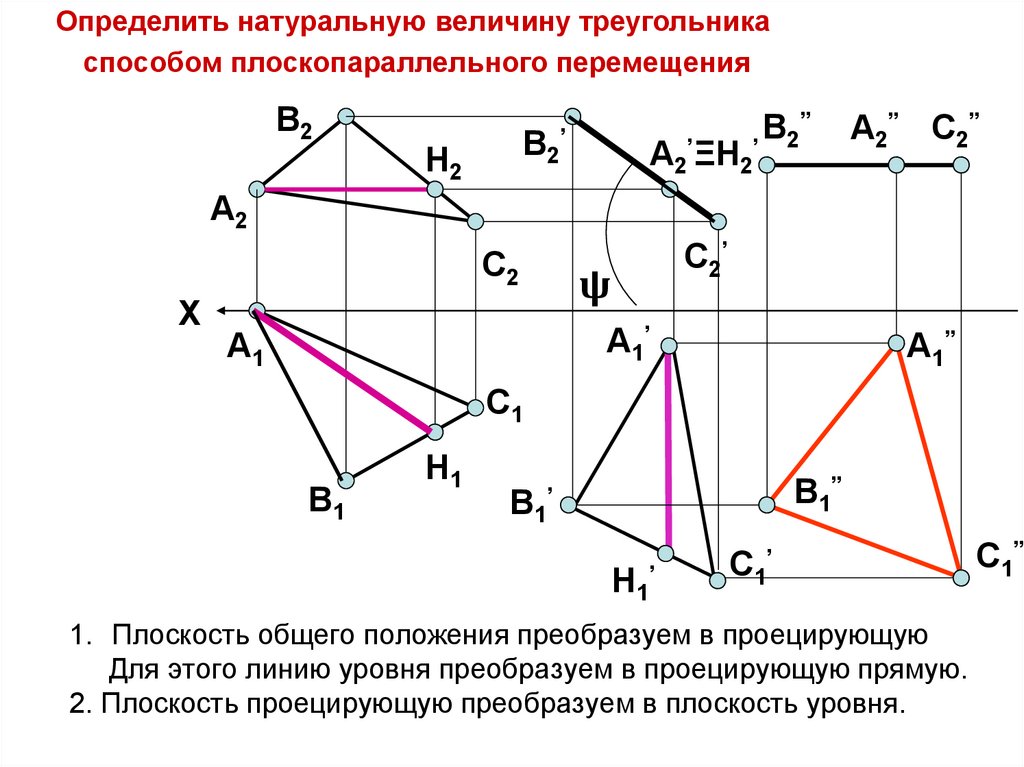
Определить натуральную величину треугольника
способом плоскопараллельного перемещения
B2
B2
H2
’
A2’ΞH2
’’
B
’ 2
A2’’ C2’’
A2
C2
C2’
ψ
X
A1’
A1
A1’’
C1
B1
H1
B1
B1’’
’
H1’
C1’
1. Плоскость общего положения преобразуем в проецирующую
Для этого линию уровня преобразуем в проецирующую прямую.
2. Плоскость проецирующую преобразуем в плоскость уровня.
C1’’

14. Сущность способа вращения вокруг прямых, перпендикулярных плоскостям проекций

• Заданный геометрический объект вращается вокруг
оси до положения параллельного или
перпендикулярного какой-либо плоскости проекций.
• Все точки объекта движутся по окружностям, которые
располагаются в плоскостях уровня,
перпендикулярных оси вращения.

15.

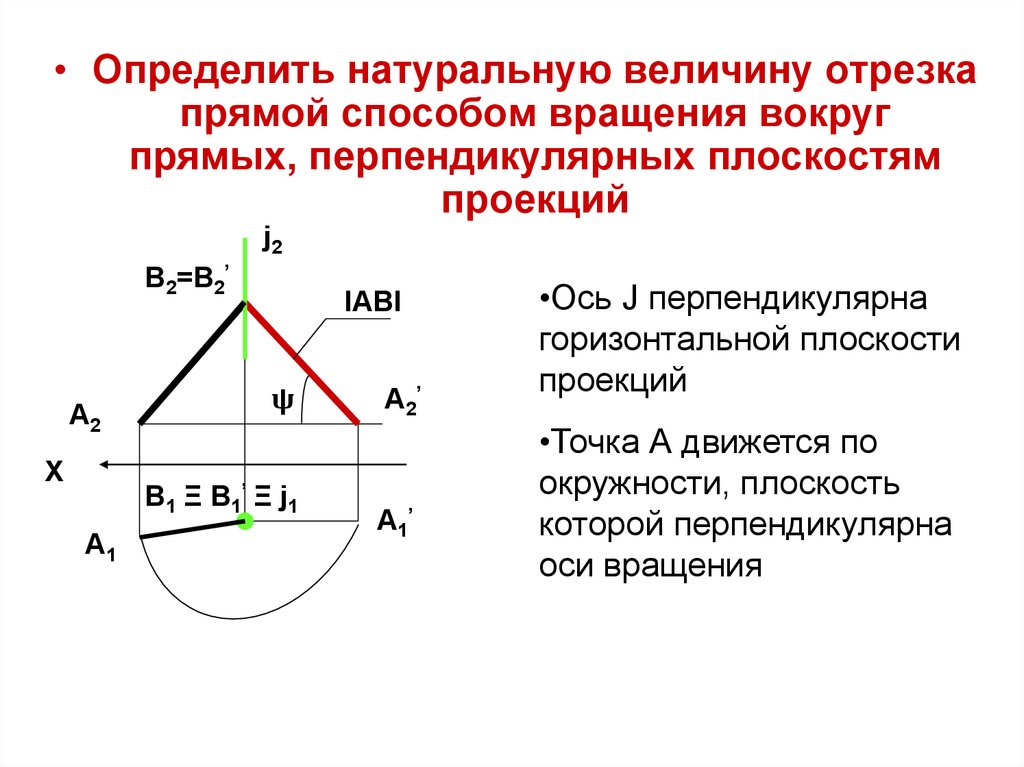
• Определить натуральную величину отрезка
прямой способом вращения вокруг
прямых, перпендикулярных плоскостям
проекций
j2
B2=В2’
A2
X
IABI
ψ
B1 Ξ В1’ Ξ j1
A1
A 2’
A 1’
•Ось J перпендикулярна
горизонтальной плоскости
проекций
•Точка А движется по
окружности, плоскость
которой перпендикулярна
оси вращения

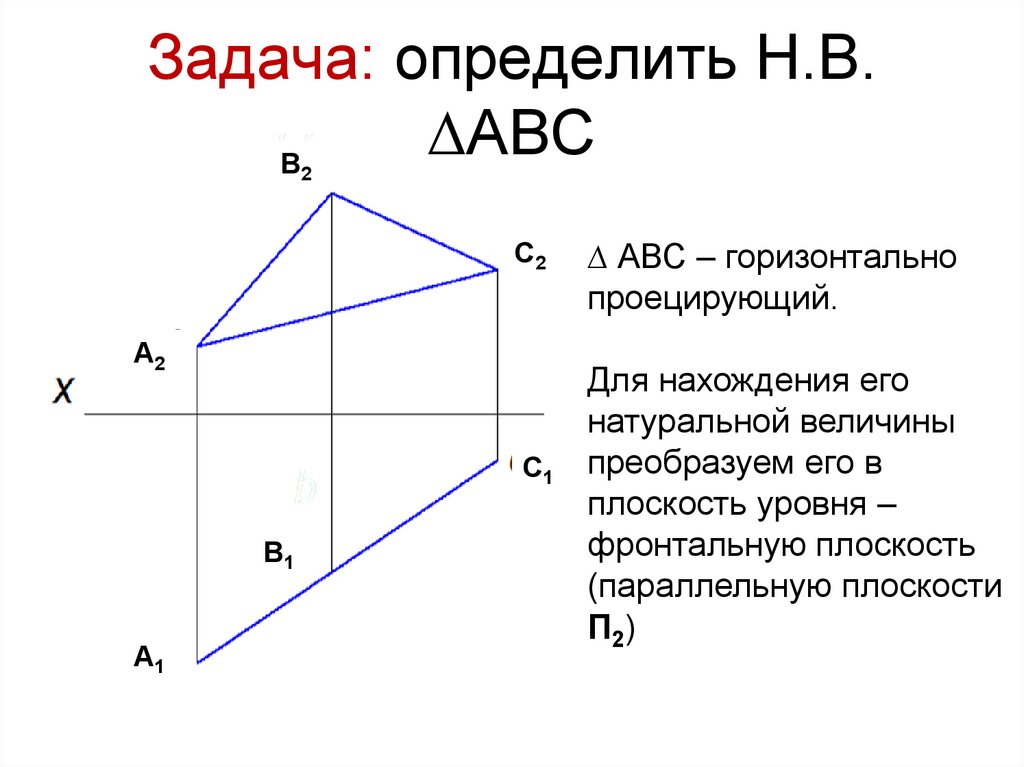
16. Задача: определить Н.В. ∆АВС

B
2
C2
A2
C1
B1
A1
∆ АВС – горизонтально
проецирующий.
Для нахождения его
натуральной величины
преобразуем его в
плоскость уровня –
фронтальную плоскость
(параллельную плоскости
П 2)

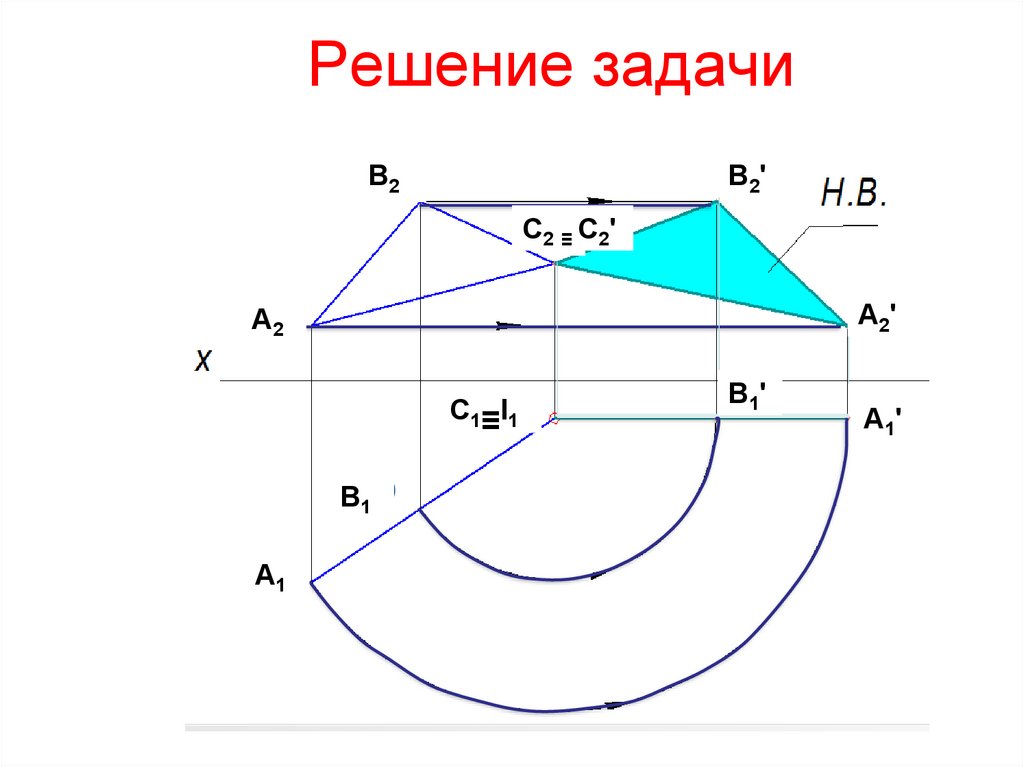
17. Решение задачи

B2
B2'
C 2 ≡ C 2'
A 2'
A2
C1≡I1
B1
A1
B 1'
A 1'

18. Спасибо за внимание!