Способы преобразования чертежа

1.

Пермский государственный технический университет
Кафедра дизайна, графики и начертательной
геометрии
Е.С. Дударь, И.Д. Столбова
Тема 4
Способы преобразования
чертежа
Цель: изучить способы преобразования чертежа,
сформировать навыки применения их при решении
метрических задач

2.

Обзор способов преобразования чертежа
1. Преобразование системы координат
• Способ перемены плоскостей проекций
• Способ дополнительного
проецирования
2. Преобразование пространства
• Способ плоскопараллельного перемещения
• Способ вращение вокруг проецирующей
прямой
• Способ вращения вокруг линии уровня
При преобразование системы координат объект в пространстве остается
неподвижной, а изменяют систему плоскостей проекций или направление
проецирования. При преобразовании пространства перемещается объект,
а система плоскостей проекций остается неизменной

3.

Способ перемены плоскостей проекций
Сущность способа: осуществляется переход
от данной системы («старая система») к
новой системе плоскостей проекций, в
которой геометрический образ займет
частное положение
• Используется метод ортогонального
проецирования
• Новая плоскость проекций П4 называется
дополнительной по отношению к основным П1,
П2, П3
• Плоскость П4 располагается перпендикулярно
одной из основных плоскостей проекций
• Плоскость П4 выбирается так, чтобы
геометрический образ по отношению к ней занял
частное положение

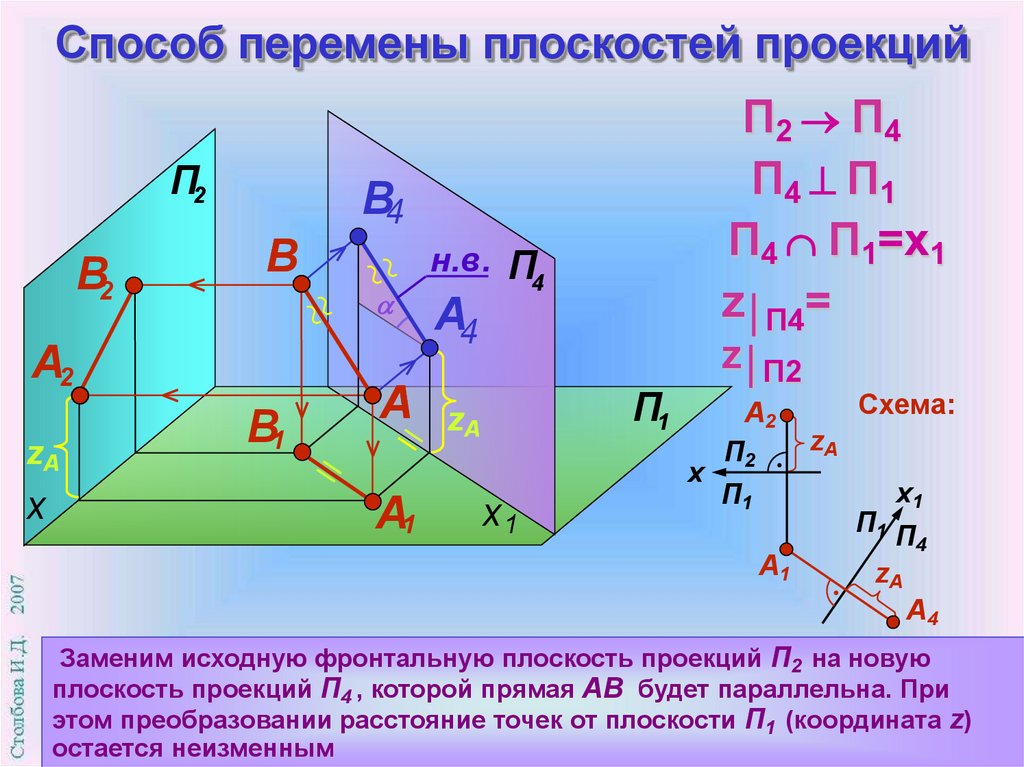
4. Способ перемены плоскостей проекций

П2
В2
В
zА
x
В4
А2
В1
П 2 П4
П 4 П1
П4 П1=x1
z П4=
А
А1
н.в. П
4
А4
П1
zА
x1
z П2
А2
П2
x
П1
А1
Схема:
zА
x1
П1 П
4
zА
А4
Заменим исходную фронтальную плоскость проекций П2 на новую
плоскость проекций П4 , которой прямая АВ будет параллельна. При
этом преобразовании расстояние точек от плоскости П1 (координата z)
остается неизменным

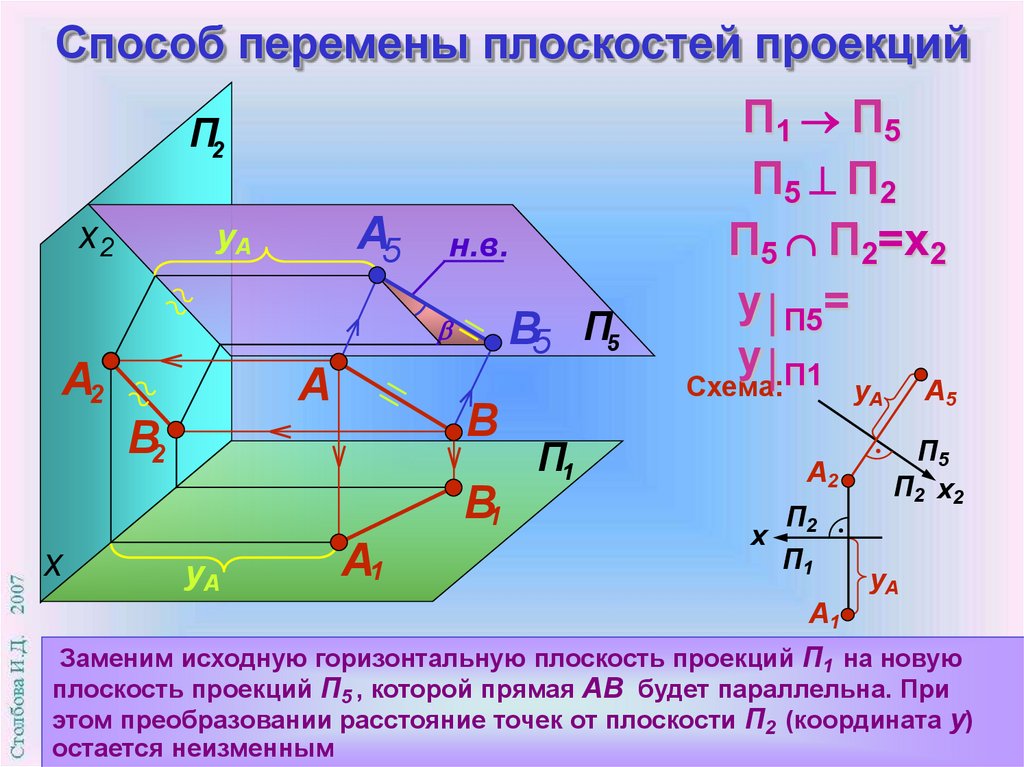
5. Способ перемены плоскостей проекций

П2
x2
А5
yА
н.в.
В5 П5
А2
А
В
В2
В1
x
yА
А1
П 1 П5
П 5 П2
П5 П2=x2
y П5=
y П1
Схема:
П1
А2
x
А5
yА
П2
П1
А1
П5
П2 x2
yА
Заменим исходную горизонтальную плоскость проекций П1 на новую
плоскость проекций П5 , которой прямая АВ будет параллельна. При
этом преобразовании расстояние точек от плоскости П2 (координата у)
остается неизменным

6.

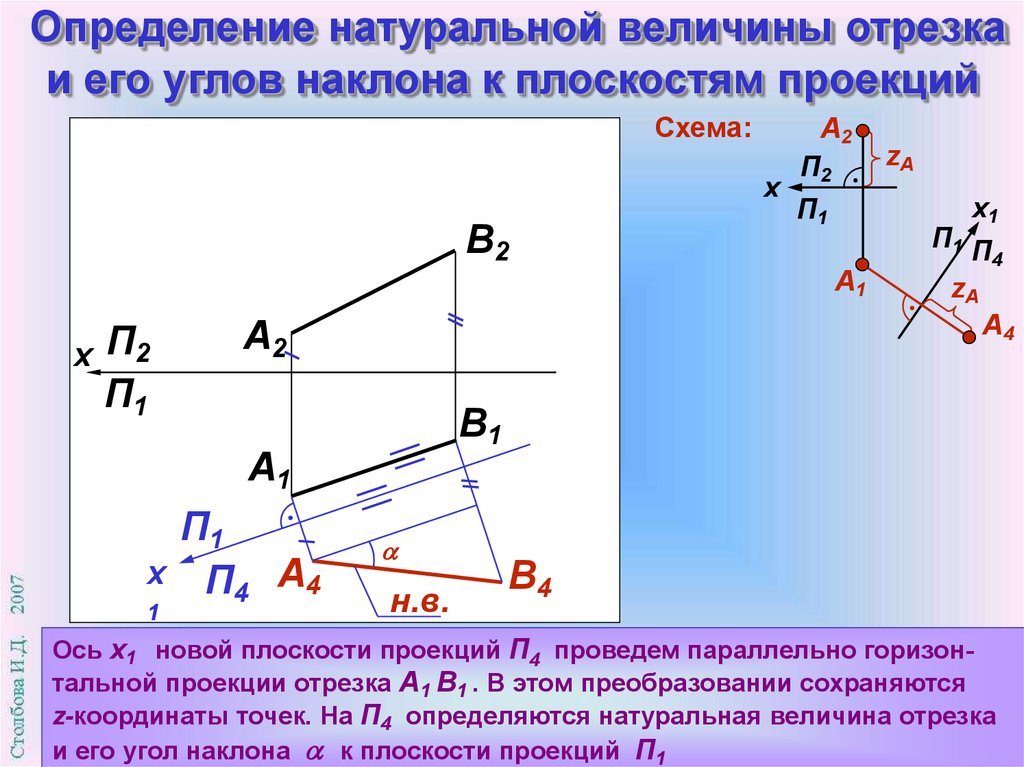
Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
Схема:
B2
x П2
А2
П1
1
А1
zА
x1
П1 П
4
zА
А4
B1
А1
П1
x П А4
4
А2
П2
x
П1
н.в.
В4
Ось х1 новой плоскости проекций П4 проведем параллельно горизонтальной проекции отрезка А1 В1 . В этом преобразовании сохраняются
z-координаты точек. На П4 определяются натуральная величина отрезка
и его угол наклона к плоскости проекций П1

7.

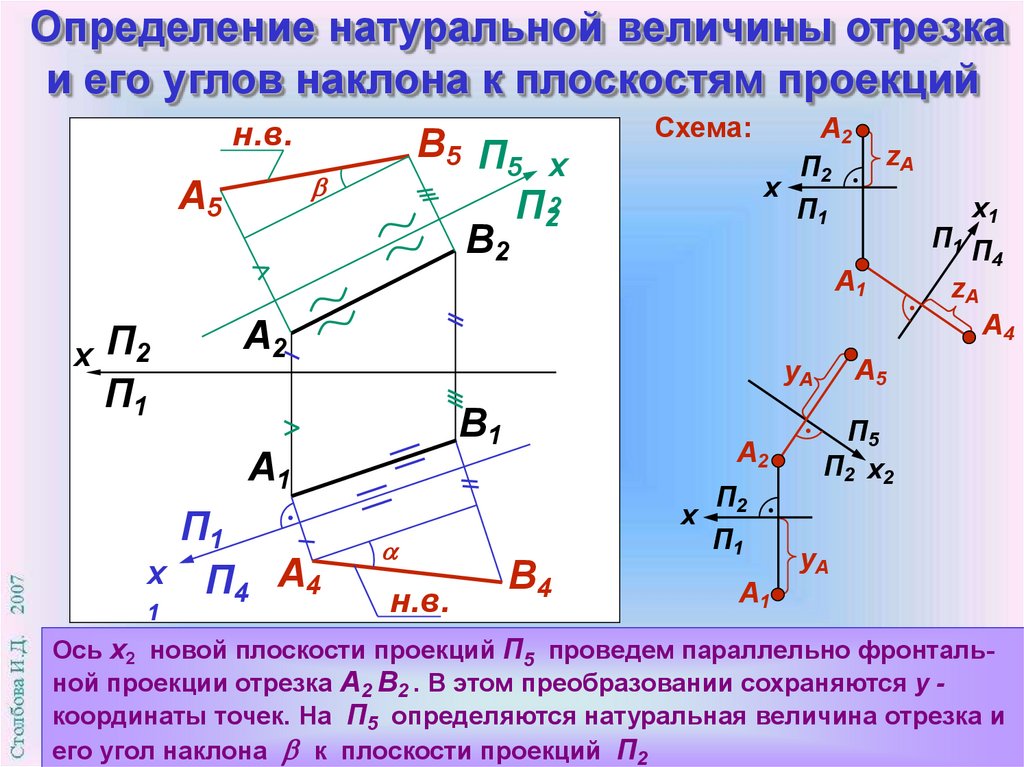
Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
н.в.
В5 П5 x
А5
B2
x П2
П22
А2
П2
x
П1
B1
П1
x П А4
4
А2
x
н.в.
В4
П2
П1
А1
x1
П1 П
4
zА
А4
А5
yА
А1
zА
А1
А2
П1
1
Схема:
П5
П2 x2
yА
Ось х2 новой плоскости проекций П5 проведем параллельно фронтальной проекции отрезка А2 В2 . В этом преобразовании сохраняются y координаты точек. На П5 определяются натуральная величина отрезка и
его угол наклона к плоскости проекций П2

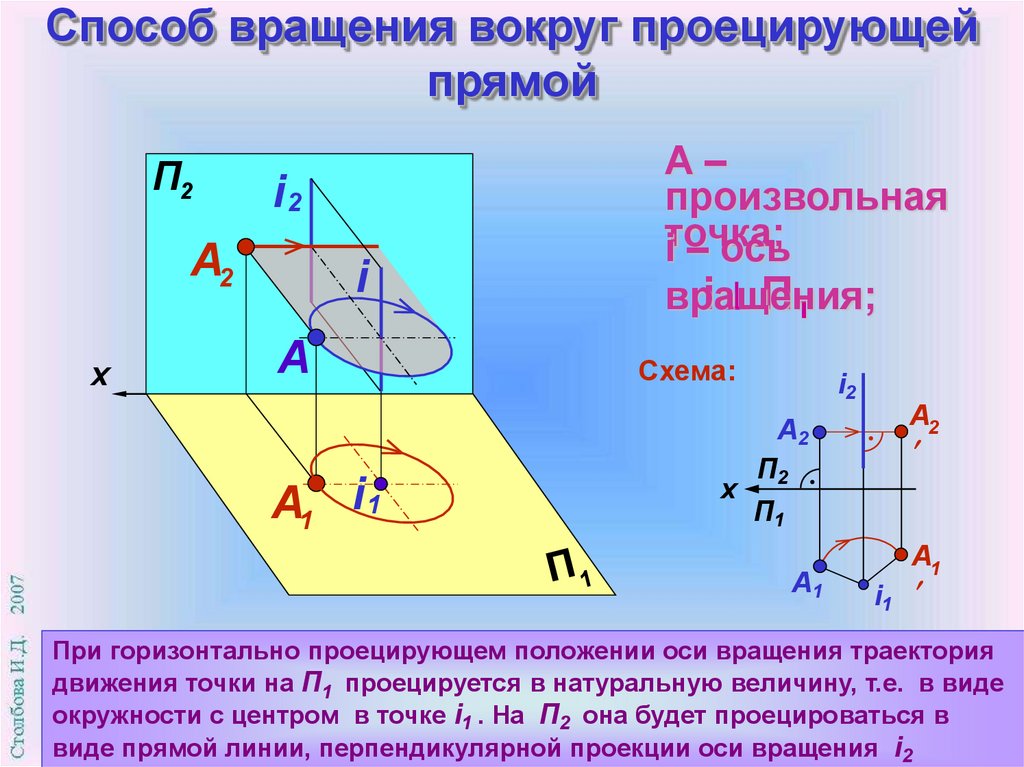
8. Способ вращения вокруг проецирующей прямой

Сущность способа:
геометрический образ
вращают вокруг проецирующей оси до частного
А – произвольная
положения
точка;
i – ось
i П2
вращения;
Схема:
П2
А2
i2
i
x
A
А1
А2
П2
x
П1
i1
А1
А2
i2
А1
i1
При вращении точка описывает окружность, расположенную в плоскости
уровня. Если ось вращения i П2 , то на П2 траектория движения точки
проецируется в натуральную величину (окружность с центром в точке i2 )
На П1 она проецируется в виде прямой, проекции оси вращения i1

9. Способ вращения вокруг проецирующей прямой

П2
i2
А2
x
i
A
А1 i 1
А–
произвольная
точка;
i – ось
вращения;
i П1
Схема:
i2
А2
П2
x
П1
А1
А2
А1
i1
При горизонтально проецирующем положении оси вращения траектория
движения точки на П1 проецируется в натуральную величину, т.е. в виде
окружности с центром в точке i1 . На П2 она будет проецироваться в
виде прямой линии, перпендикулярной проекции оси вращения i2

10.

Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
Схема:
i2
В2
А2
l2
н.в.
A2
x
А1
B1 l 1
А2
П2
x
П1
А1
А2
А1
i1
A1
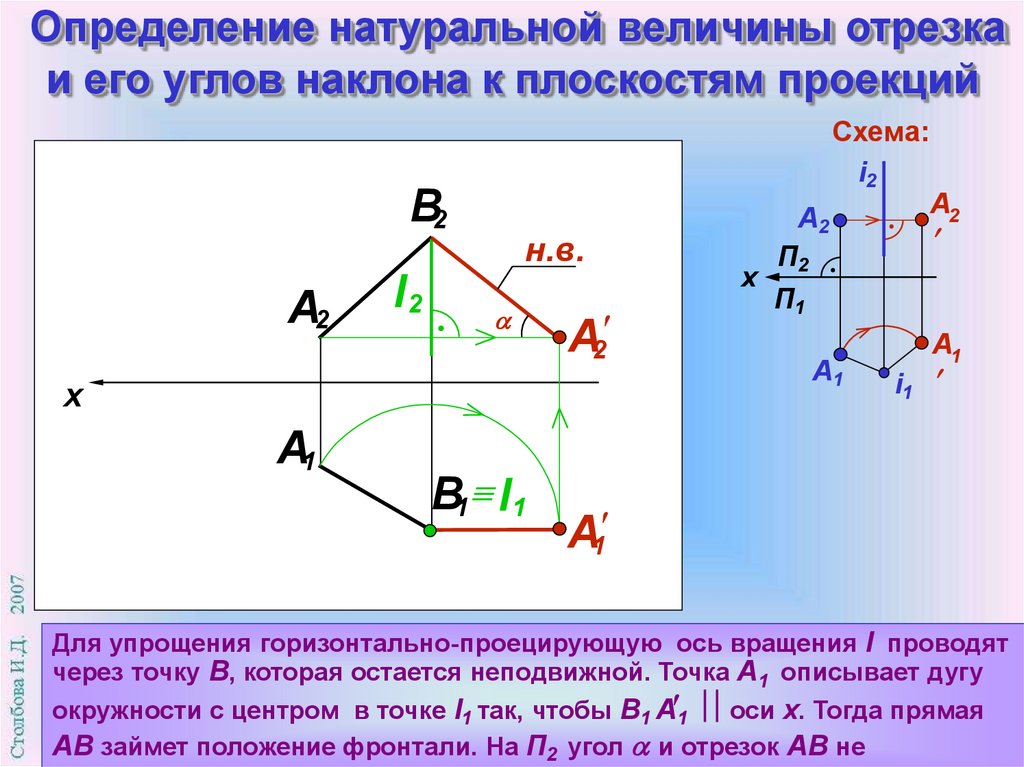
Для упрощения горизонтально-проецирующую ось вращения l проводят
через точку В, которая остается неподвижной. Точка А1 описывает дугу
окружности с центром в точке l1 так, чтобы В1 А 1 оси х. Тогда прямая
АВ займет положение фронтали. На П2 угол и отрезок АВ не

11.

Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
Схема:
i2
В2
B2
i2 А2
l2
н.в.
A2
x
н.в. А1
B1
B1 l 1
i1
A1
А2
П2
x
П1
А1
А1
А2
П2
x
П1
А1
А2
i1
А2
i2
А1
i1
Для определения угла прямую АВ нужно вращать вокруг оси i П2 до
положения горизонтали. Ось проходит через точку А, которая
неподвижна. Точка В2 вращается по дуге окружности с центром в точке i2
до положения В2 А2 оси х. На П1 угол и отрезок АВ не искажаются

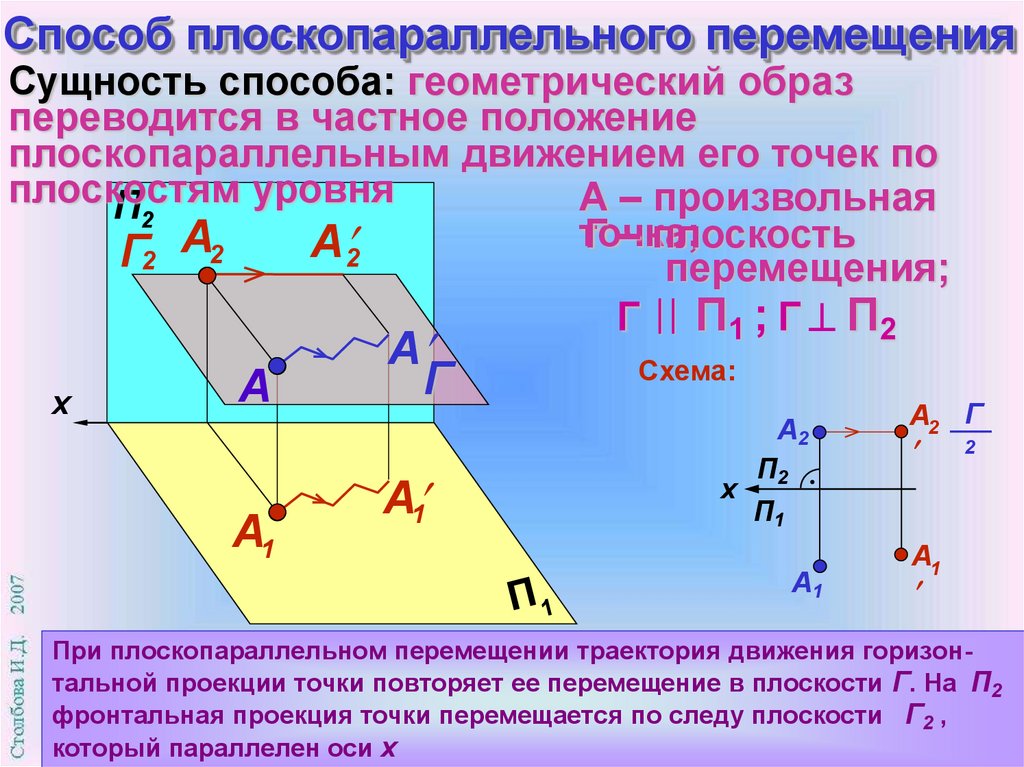
12. Способ плоскопараллельного перемещения

Сущность способа: геометрический образ
переводится в частное положение
плоскопараллельным движением его точек по
плоскостям
уровня
А – произвольная
П2
точка;
Г – плоскость
А 2
Г2 А2
перемещения;
Г П1 ; Г П2
x
A
А1
А
Г
А1
Схема:
А2
П2
x
П1
А1
А2 Г
2
А1
При плоскопараллельном перемещении траектория движения горизонтальной проекции точки повторяет ее перемещение в плоскости Г. На П2
фронтальная проекция точки перемещается по следу плоскости Г2 ,
который параллелен оси х

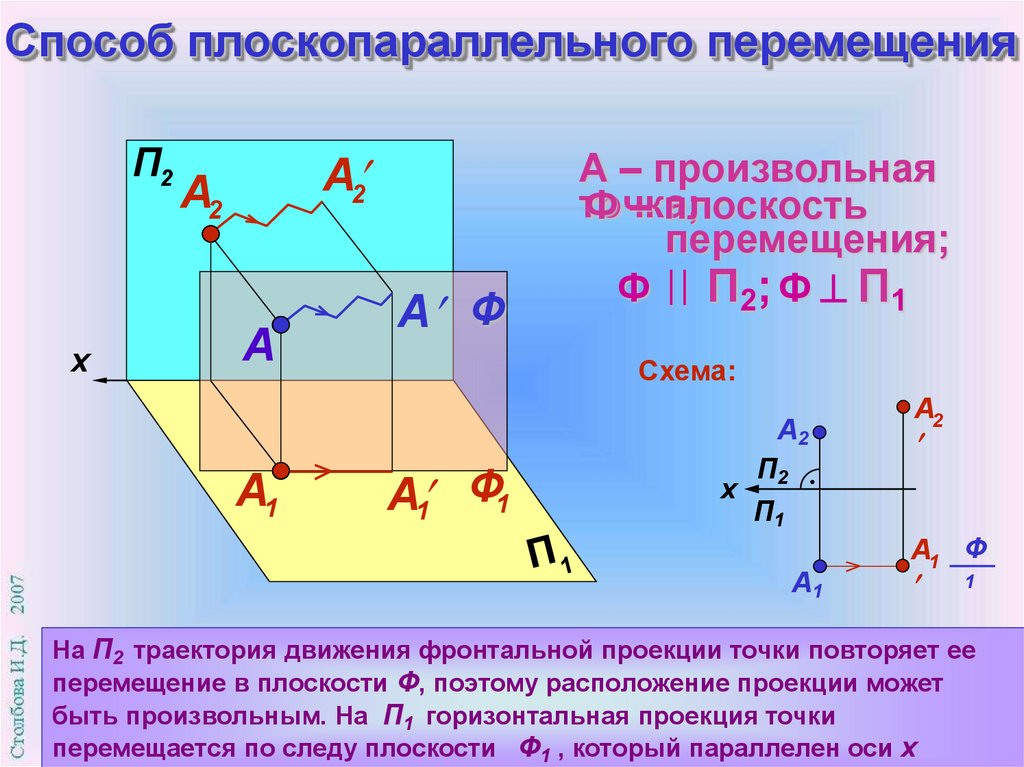
13. Способ плоскопараллельного перемещения

П2
x
А2
А2
A
А1
А Ф
А – произвольная
точка;
Ф – плоскость
перемещения;
Ф П2; Ф П1
Схема:
А1 Ф1
А2
П2
x
П1
А1
А2
А1 Ф
1
На П2 траектория движения фронтальной проекции точки повторяет ее
перемещение в плоскости Ф, поэтому расположение проекции может
быть произвольным. На П1 горизонтальная проекция точки
перемещается по следу плоскости Ф1 , который параллелен оси х

14.

Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
Схема:
В2
А2
А2
П2
x
П1
А1
x
А1
B1
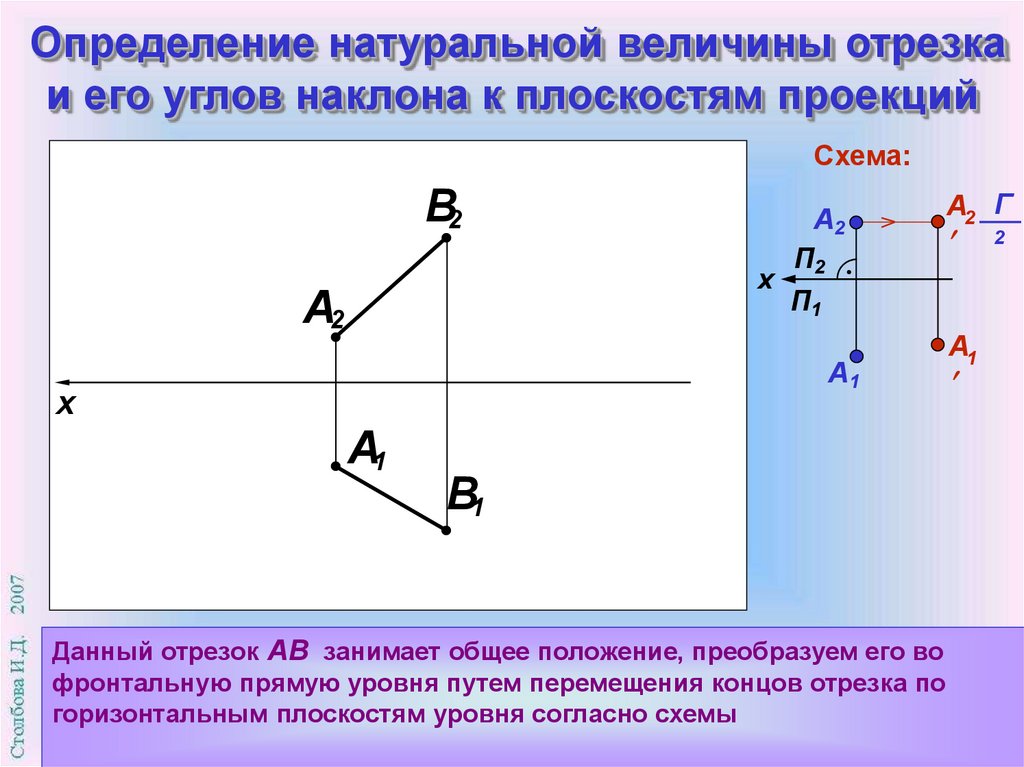
Данный отрезок АВ занимает общее положение, преобразуем его во
фронтальную прямую уровня путем перемещения концов отрезка по
горизонтальным плоскостям уровня согласно схемы
А2 Г
А1
2

15.

Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
Схема:
В2
B2 Г
А2
2 н.в.
A2 Г
2
x
А1
B1 В1
А2
П2
x
П1
А1
А2 Г
2
А1
A1
Горизонтальную проекцию прямой (А1 В1 А1 В1 ) располагают
параллель-но оси х. Фронтальную проекцию (определяющую н.в. отрезка
и угла ) задают новые проекции точек
А2 и В2 , расположенные на
соответствую-щих следах горизонтальных плоскостей уровня Г(Г2 ) и

16.

Определение натуральной величины отрезка
и его углов наклона к плоскостям проекций
Схема:
А2
B2
В2
B2 Г
А2
2 н.в.
A2 Г
2
x
н.в. Ф
Ф
1
B1
1
А1
А1
B1 В1
A1
А2
П2
x
П1
А1
А2
П2
x
П1
Ф
1 А1
А2 Г
2
А1
А2
А1
Для перевода прямой в положение горизонтали фронтальную проекцию
прямой (А2 В2 А2 В2 ) располагают параллельно оси х. Новые проекции
точек А
1 и В
1 расположены на соответствующих следах фронтальных
плоскостей уровня Ф(Ф1 ) и Ф (Ф1 ) . На П1 имеем н.в. отрезка и угла

17. Способ вращения вокруг линии уровня

П2 А2
r2
O2
h2
A
r h
O
x
А1r
1
O1
Сущность способа:
геометрический образ
вращается вокруг линии
уровня до частного положения
А – произвольная
точка;
h – горизонтальная
ось вращения
h1
1
При вращении точки А вокруг линии уровня плоскость окружности (r,O),
перпендикулярная h , будет горизонтально проецирующей П1 ( 1 h1
). Горизонтальная траектория перемещения точки будет принадлежать
следу 1 , длина которого равна диаметру или 2r

18. Определение натуральной величины треугольника

B
12 2
O2
h2 B C
2
2
A
2
A
1
O1
11
B
C
h1
1
н.в. rB
B
1
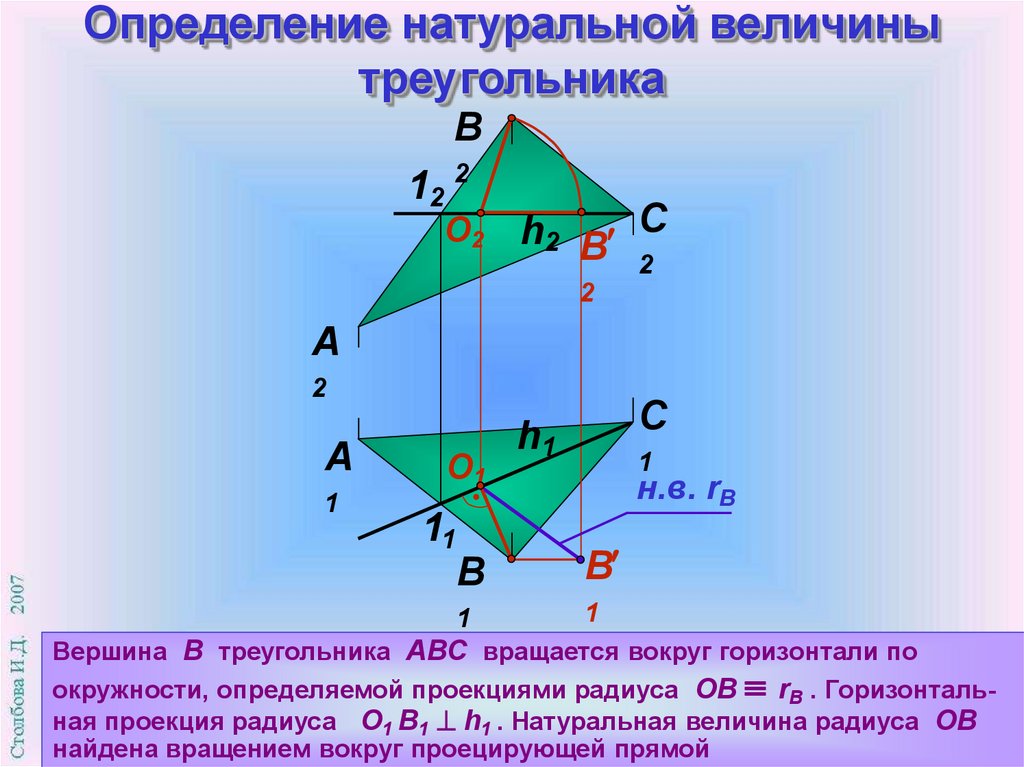
Вершина В треугольника АВС вращается вокруг горизонтали по
окружности, определяемой проекциями радиуса ОВ rВ . Горизонтальная проекция радиуса О1 В1 h1 . Натуральная величина радиуса ОВ
найдена вращением вокруг проецирующей прямой
1

19. Определение натуральной величины треугольника

B
A2
O 2 12
2
O2
h2 B C
2
2
A
A1
н.в. rА
2
A
1
O1
O 1 11
B
C
h1
1
н.в. rB
B
1
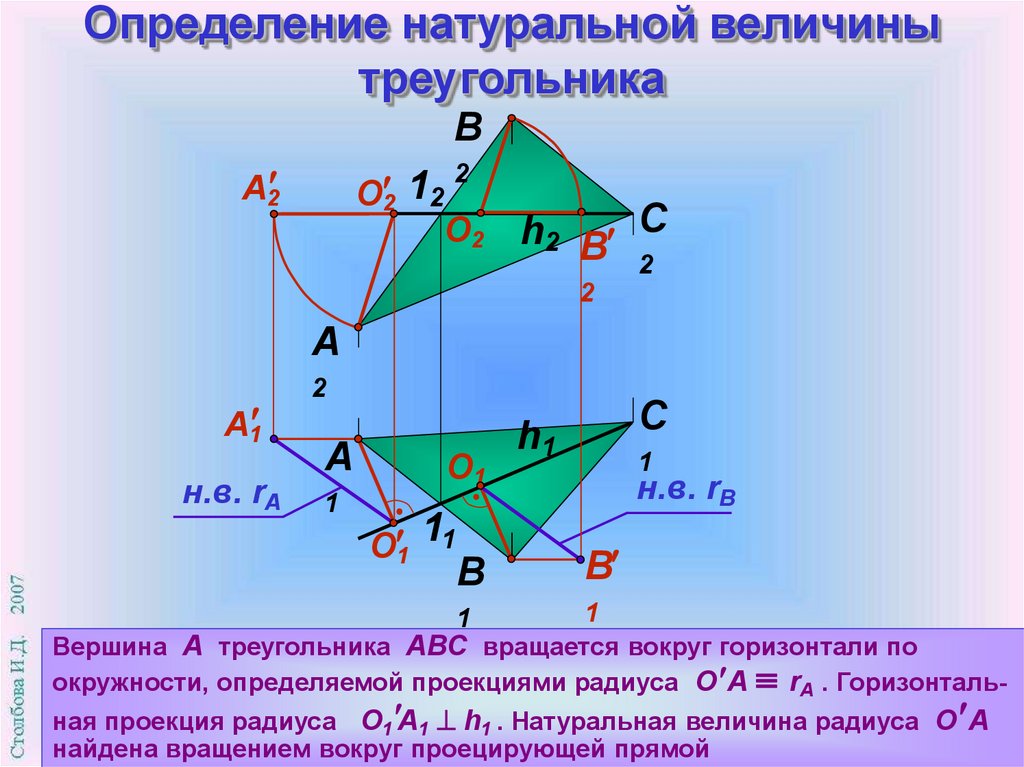
Вершина А треугольника АВС вращается вокруг горизонтали по
окружности, определяемой проекциями радиуса О А rА . Горизонтальная проекция радиуса О1 А1 h1 . Натуральная величина радиуса О А
найдена вращением вокруг проецирующей прямой
1

20. Определение натуральной величины треугольника

B
A2
O 2 12
2
h2 B C
O2
2
2
A
A1
н.в. rА
2
0
A
1
A
1
O1
O 1 11
C
h1
B
0
1B
1
н.в. rB
B
1
1
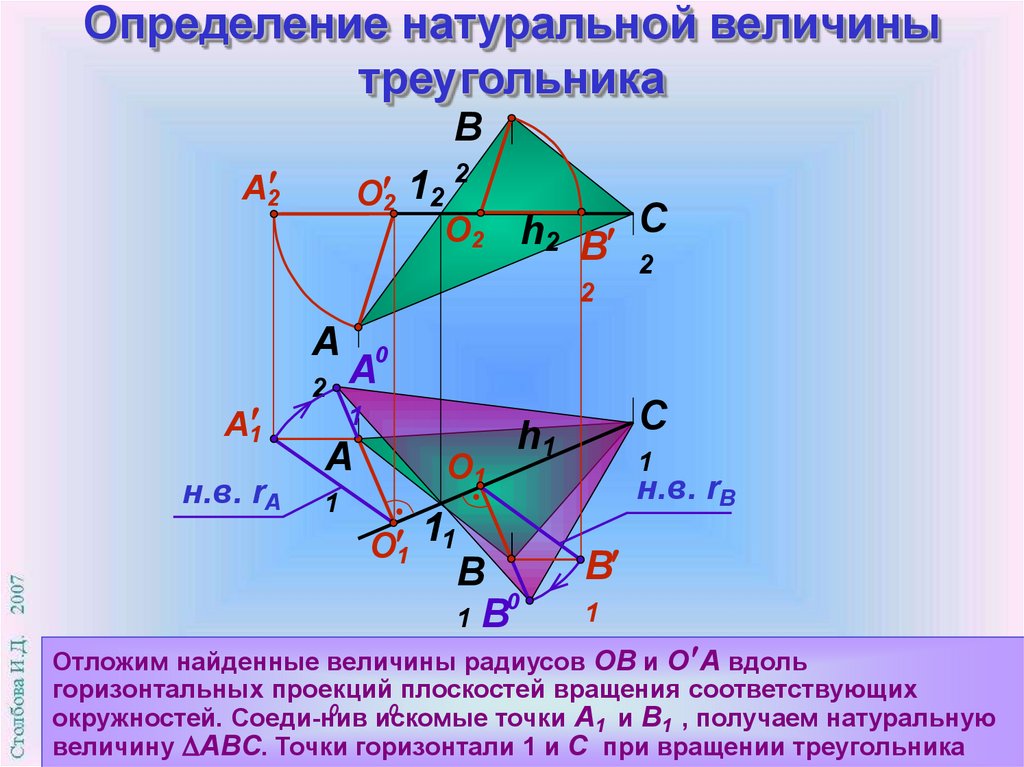
Отложим найденные величины радиусов
ОВ и О А вдоль
горизонтальных проекций плоскостей вращения соответствующих
0
0
окружностей. Соеди-нив
искомые
точки А1 и В1 , получаем натуральную
величину АВС. Точки горизонтали 1 и С при вращении треугольника

21.

Вопросы для самопроверки
1. Какая координата остается неизменной при замене
плоскости П1?
а) x
б) y
в) z
2. Какая координата остается неизменной при замене
плоскости П2?
а) x
б) y
в) z
3. Какую плоскость проекций надо заменить, чтобы
найти угол наклона прямой общего положения к
плоскости проекций П1?
а) П1
б) П2
в) П3

22.

Вопросы для самопроверки
4. Какую плоскость проекций надо заменить, чтобы
найти угол наклона прямой общего положения к
плоскости проекций П2?
а) П1
б) П2
в) П3
5. Какой плоскости проекций перпендикулярна ось
вращения, если фронтальная проекция точки
перемещается по прямой, параллельной оси Ох?
а) П1
б) П2
в) П3
6. Какой плоскости проекций перпендикулярна ось
вращения, если фронтальная проекция точки
перемещается по дуге окружности?
а) П1
б) П2
в) П3

23.

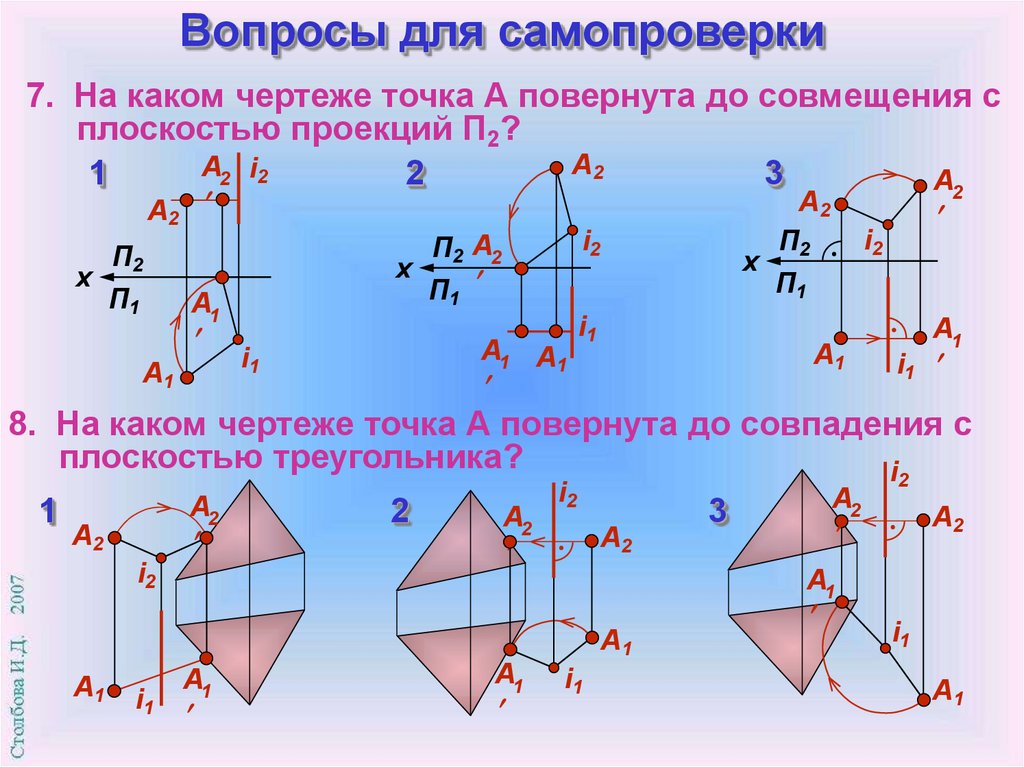
Вопросы для самопроверки
7. На каком чертеже точка А повернута до совмещения с
плоскостью проекций П2?
А2
А2 i2
1
2
3
А2
А2
П2
x
П1
П2 А2
x
П1
А1
А1
i2
А1 А1
i1
А2
П2
x
П1
i1
i2
А1
А1
i1
8. На каком чертеже точка А повернута до совпадения с
плоскостью треугольника?
i
1
А2
А2
2
А2
i1
А1
А2
i2
А1
i2
А1
А2
3
2
А2
А1
А1
i1
i1
А1

24.

Вопросы для самопроверки
9. Установите соответствие названий способов и
чертежей со схемами преобразования точки А:
А2
1
П2
x
П1
А1
А2
А1
2
А2
П2
x
П1
А1
А2
i2
А2
А1
i1
А5
yА
3
П2
x
П1
А1
а) способ перемены плоскостей проекций – рис.?
б) способ плоскопараллельного перемещения – рис.?
в) способ вращения вокруг проецирующей прямой – рис.?
П5
П2 x2
yА
10. Как перемещаются точки геометрического образа при
плоскопараллельном перемещении?
а) по окружности
б) по прямой
в) в плоскостях уровня

25.

Вопросы для самопроверки
11. На каком чертеже угол является углом наклона
прямой АВ к плоскости проекций П1?
А
А
А2
1А
2
3 2
А2
А
2
2
В2
В2
2
В
В
В
2
А
В А
1
1
1
В1
2
А
В
1
А1
1
2
В1
А
В
1
1
А1
12. На каком чертеже правильно построены проекции
радиуса вращения точки А вокруг заданной прямой?
А
О
О
А
1
2
3
2
2
2
2
О
А
2
2
О
1
А
О
А
1
А
1
О
1

26.

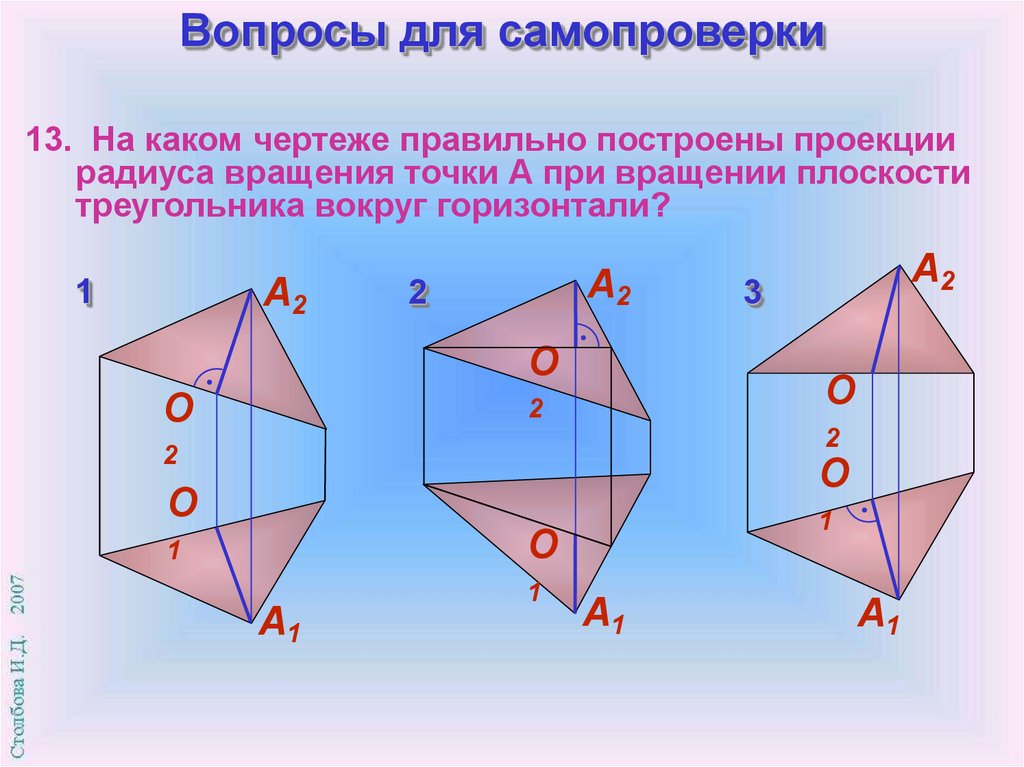
Вопросы для самопроверки
13. На каком чертеже правильно построены проекции
радиуса вращения точки А при вращении плоскости
треугольника вокруг горизонтали?
А2
1
А2
2
О
О
А2
3
О
2
2
2
О
О
1
О
1
А1
1
А1
А1