Similar presentations:
Основы векторной алгебры
1. Лекция 8 Основы векторной алгебры (I)
2. Векторы (Vectors)
Опр. Вектором (геометрическим) (Euclidean)называется
отрезок,
концы
которого
упорядочены. Первый из его концов называется
началом, второй – концом вектора.
Опр. Нулевой вектор (zero vector) - вектор, у
которого начало и конец совпадают:
0
3.
Опр. Модуль (длина) вектора – это расстояниемежду его началом и концом:
a , MN .
Опр. Единичный вектор (unit vector): | e | 1.
Опр. Коллинеарные (collinear) векторы – векторы,
лежащие на одной прямой или на параллельных
прямых.
a
b
a
b
,
a || b,
a : a ||0.
4.
Опр. Компланарные (coplanar) векторы – векторы,лежащие в одной плоскости или в параллельных
плоскостях.
Опр. Равные векторы:
a b a b a b .
Векторы бывают свободными, скользящими и
связанными.
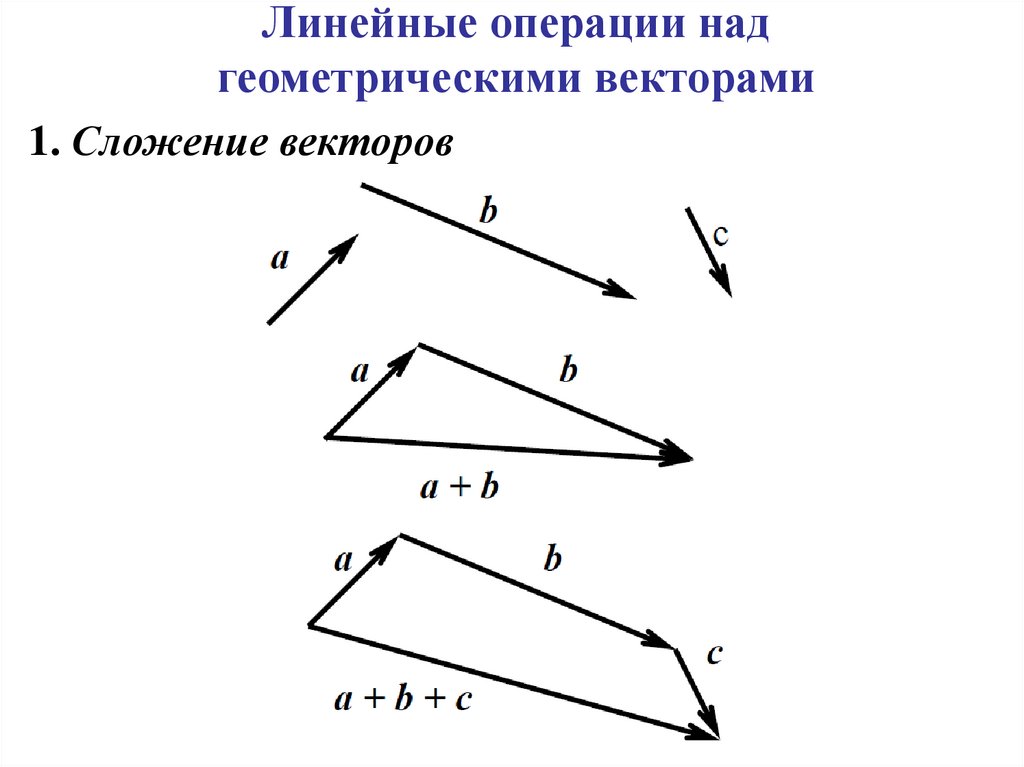
5. Линейные операции над геометрическими векторами
1. Сложение векторов6.
2. Умножение вектора на число:b a b a 0 b a 0
b a , R.
3. Деление вектора на число:
a
1
b , 0 b a, 0 .
7. Свойства линейных операций над векторами
4. Вычитание векторов:c a b c a ( 1) b .
Свойства линейных операций над векторами
4. a 0 a : a a 0
3. a 0 a
5. a a a , , R
6. a a a 7. a b a b.
1. a b b a
2. a b c a b c
Упр. Доказать любые три свойства.
8.
Опр. Линейная комбинация векторов (linearcombination of vectors):
n
a a a ... a , R
i 1
i
i
1 1
2
2
n
n
i
где αi – коэффициенты ЛК.
Опр. Линейно независимая (ЛНЗ) система
векторов {ai} (i=1,..,n):
i ai 0 i 0 i 1, n
i 1
n
9.
Опр. Линейно зависимая (ЛЗ) система векторов{ i , i 1, n
n
2
i 0}: i ai 0
i 1
i 1
n
Т. Если векторы a1, a2,…, an ЛЗ, то хотя бы один из
них может быть представлен в виде ЛК остальных.
Доказательство.
n
1 0 : i ai 0 1 a1 i ai
i 1
i 2
n
i
a1 ai .
i 2 1
n
10.
Опр. Разложение вектора b по системевекторов {ai}
n
i , i 1, n
: b i ai .
i 1
n
Т. b i ai единственно
i 1
a , i 1, n ЛНЗ .
Т. a , i 1, n ЛЗ a
a .
i
i
j
i j
i
i
11.
2. a , a , a ЛЗ a , a , a компланарны ;Следствия. 1. a1 , a2 ЛЗ a1 || a2 ;
1
2
3
1
2
3
3. a1 , a2 , a3 , a4 ЛЗ.
Упр. Доказать п.1 следствия.
Опр. Множество векторов, замкнутое относительно
линейных операций над ними, называется
векторным пространством (vector space) Vn,
Rn. Характеризуется размерностью (dimension) n.
12.
Базис в векторном пространствеОпр. Базисом (basis) в R3 называется
упорядоченная система ЛНЗ векторов {ei}, i=1,2,3
такая, что любой вектор может быть представлен в
виде ЛК этих векторов:
a a1 e1 a2 e2 a3 e3
( )
Опр.
Коэффициенты
разложения
(*)
называются координатами (coordinates) или
компонентами вектора в данном базисе :
a (a1 , a2 , a3 ).
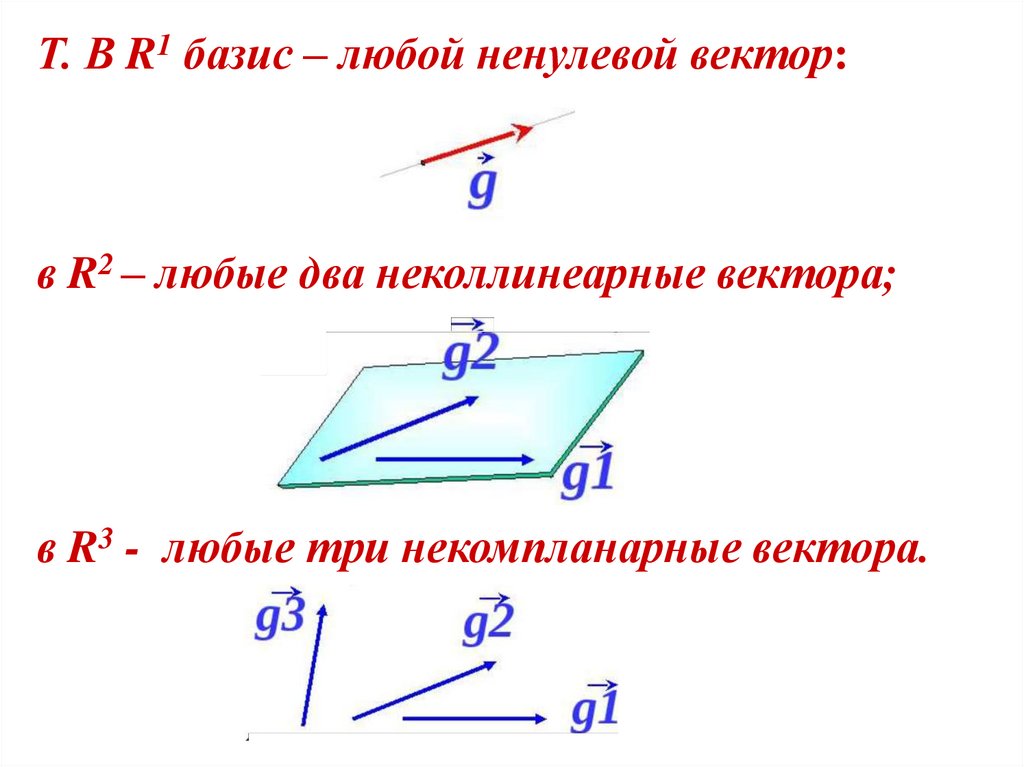
13.
Т. В R1 базис – любой ненулевой вектор:в R2 – любые два неколлинеарные вектора;
в R3 - любые три некомпланарные вектора.
14.
Выражение операций над векторамичерез их координаты
Т. Пусть векторы заданы в одном базисе. Тогда
a b (a b , a b , a b ) ;
2. a (a , a , a ), R
a ( a , a , a ) .
1. a (a1 , a2 , a3 ), b (b1 , b2 , b3 )
1
1
1
2
2
2
3
3
1
2
3
3
15.
Доказательство (1).a a1 e1 a2 e2 a3 e3 ,
b b1 e1 b2 e2 b3 e3
a b a1 e1 a2 e2 a3 e3
b1 e1 b2 e2 b3 e3
a1 b1 e1 a2 b2 e2 a3 b3 e3
a b (a1 b1 , a2 b2 , a3 b3 ).
16.
Следствие. Условие коллинеарности векторовa (a1 , a2 , a3 ), b (b1 , b2 , b3 ).
ai
a || b 0 :
.
bi
Утв. Условие компланарности векторов a, b, c:
a1 a2
a, b, c компланарны b1 b2
c1 c2
a3
b3 0.
c3
17.
П. Показать, что векторы a, b, c, образуют базистрехмерного пространства и найти координаты
вектора d в этом базисе.
a (4;1; 4); b ( 2; 1;1);
c (3;1;5); d ( 3; 2;1).
4 1 4 4 1 4
2 5
2 1 1 2 0 5 1
7 0.
1 1
3 1 5 1 0 1
18.
Так как Δ≠ 0,то векторы образуют базис. Тогдаd a b c
3
4
2
3
2 1 1 1
1
4
1
5
4 2 3 3
1
1 1 1 2 2 d
4 1 5 1
1
d a 2b c .
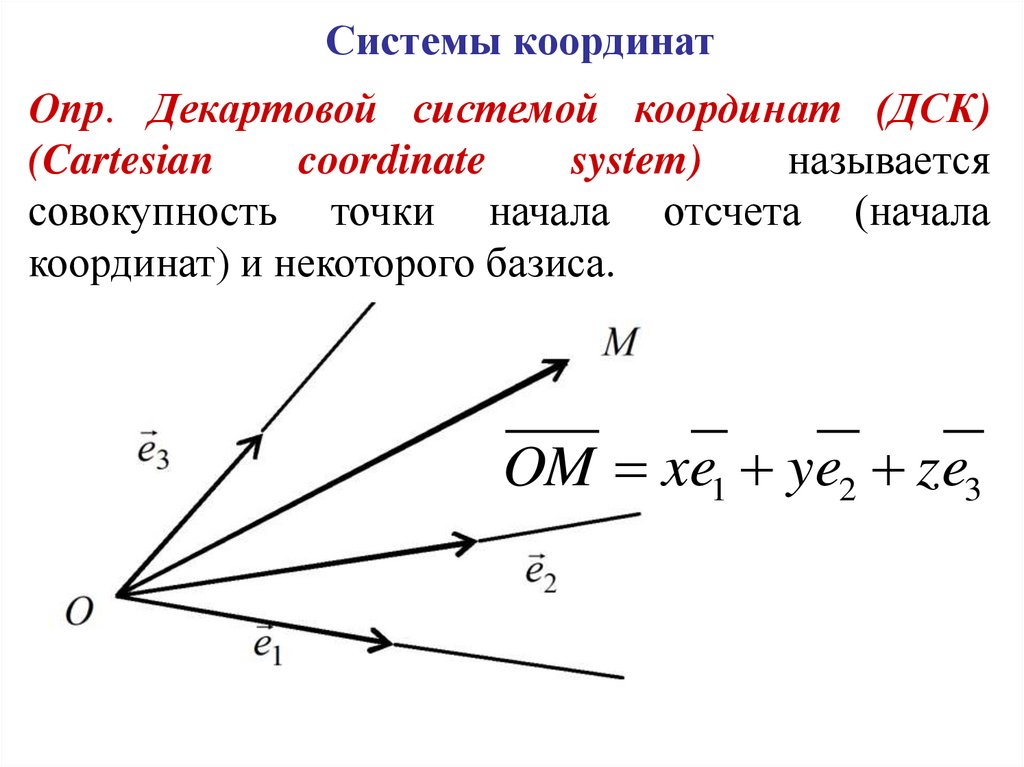
19.
Системы координатОпр. Декартовой системой координат (ДСК)
(Cartesian
coordinate
system)
называется
совокупность точки начала отсчета (начала
координат) и некоторого базиса.
OM xe1 ye2 ze3
20.
Утв. Декартовы координаты вектораAB xB xA ; yB y A ; zB z A .
Упр. Доказать утверждение.
Опр. Орт вектора (normalized vector):
a
a
.
|a|
0
Опр. Ортонормированный (orthonormal) базис
(ОНБ) – базис, векторы которого единичны и
попарно ортогональны.
21.
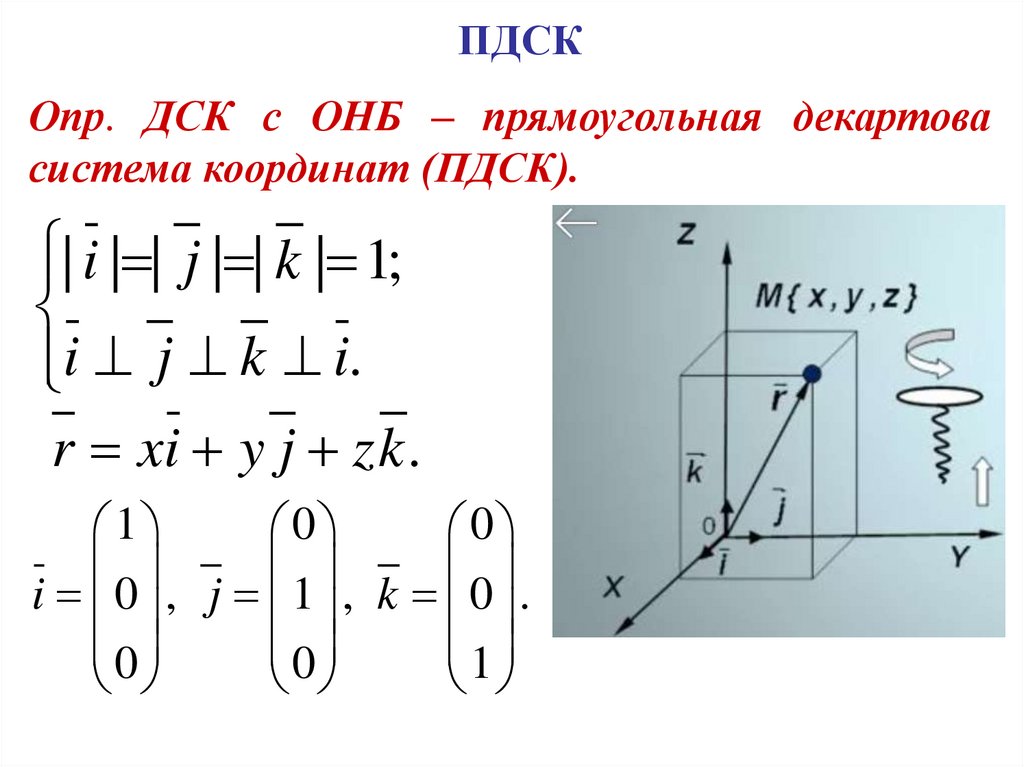
ПДСКОпр. ДСК с ОНБ – прямоугольная декартова
система координат (ПДСК).
| i | | j | | k | 1;
i j k i.
r xi y j zk .
1
0
0
i 0 , j 1 , k 0 .
0
0
1
22.
Полярная СК (ПСК), Polar coordinatesystem
Polar axe – полярная ось
Polar angle – полярный
угол
0 r ;
0 2 ;
x r cos ,
y r sin .
23.
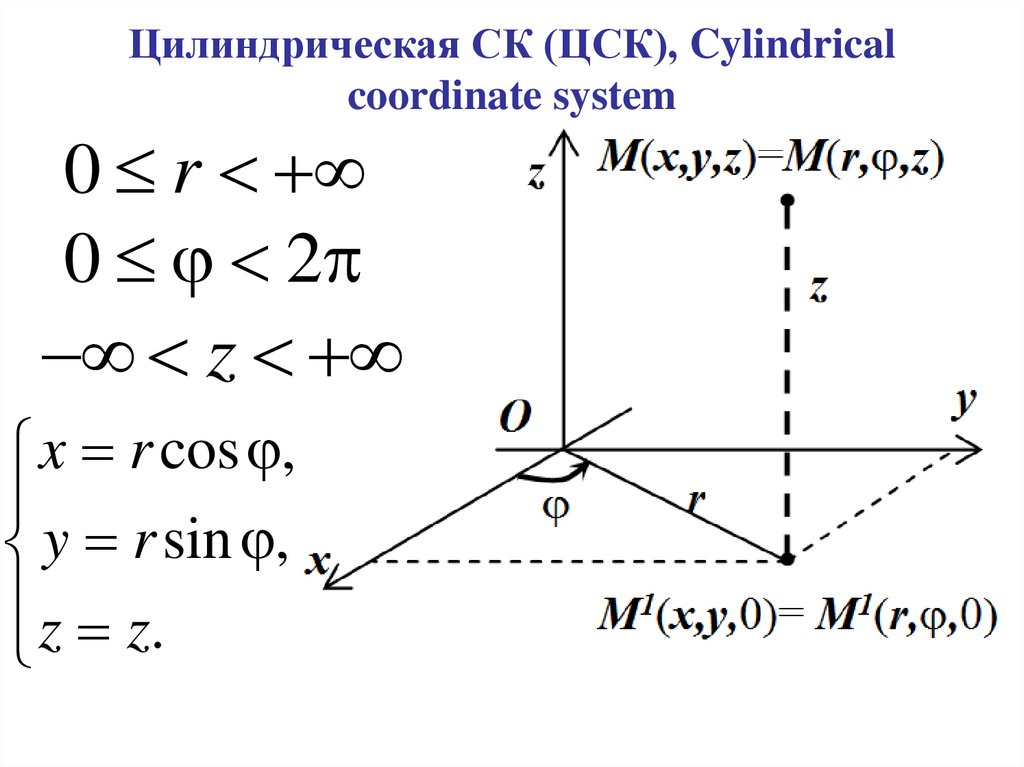
Цилиндрическая СК (ЦСК), Cylindricalcoordinate system
0 r
0 2
z
x r cos ,
y r sin ,
z z.
24.
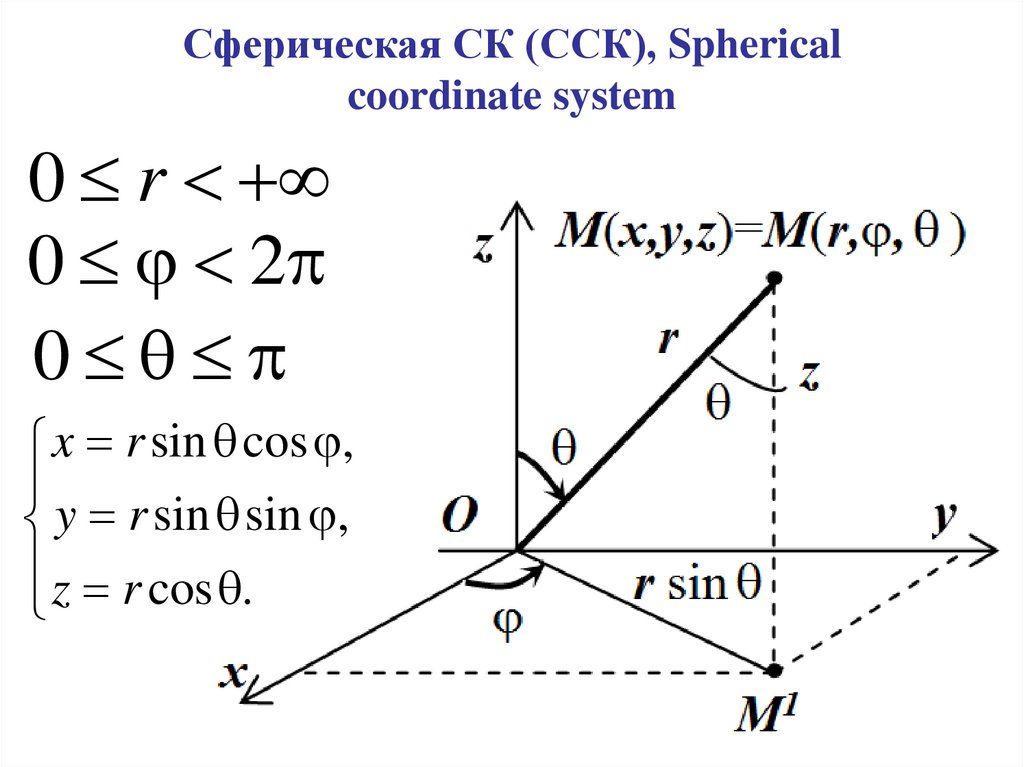
Сферическая СК (ССК), Sphericalcoordinate system
0 r
0 2
0
x r sin cos ,
y r sin sin ,
z r cos .
25. Лекция 9 Основы векторной алгебры (II)
26. Скалярное произведение векторов
A F S cosОпр. Скалярное произведение (dot product, scalar
product) векторов:
.
a, b a b a b cos
def
27. Свойства скалярного произведения
3. a, b 0 a b a 0 b 0 ;4. a b, c a, c b, c ;
2
1. a, b b, a ; 2. a, a a ;
1, if i j
5. {ei } ОНБ (ei , e j ) ij
0, else
.
Упр. Доказать свойства 2-4.
28.
Т. (выражение СП через координаты). В ОНБa, b a b a b a b ,
1 1
где
2 2
3 3
a (a1 , a2 , a3 ), b (b1 , b2 , b3 ).
Доказательство
a, b a i a j a k , b
1
2
3
.
a1 (i, b) a2 ( j, b) a3 (k , b)
a1b1 a2b2 a3b3 .
29.
Следствие. В ОНБ| a | a a a .
2
1
2
2
2
3
a, b
cos
a b
a1b1 a2b2 a3b3
.
a a a b b b
2
1
2
2
2
3
2
1
2
2
2
3
Ортогональные векторы a, b 0.
30.
Проекция вектора а на прямую, заданнуювектором l
a, l
a, l
Pr a | a | cos | a |
.
l
a1l1 a2 l2 a3l3
l l l
2
1
2
2
2
3
|l | | a |
|l |
31.
Проекции вектора а на оси ПДСК:a, i
Pr a
a | a | cos ;
i
1
|i|
Pr j a a2 | a | cos ; Prk a a3 | a | cos .
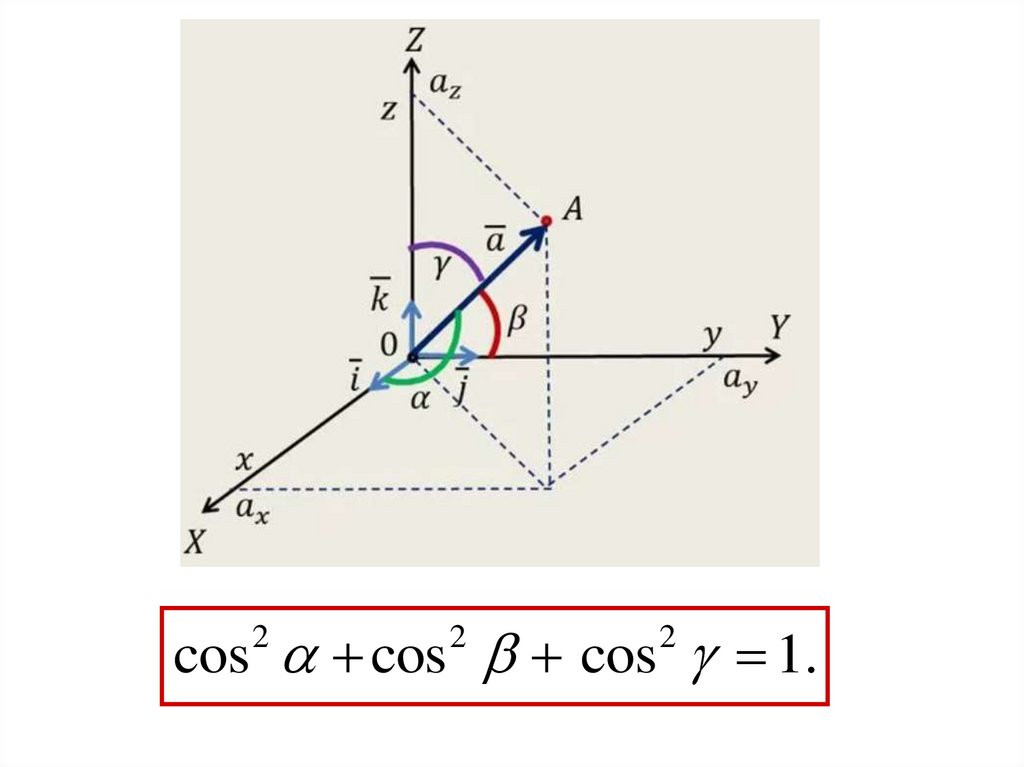
Опр. Направляющие косинусы (direction
cosines) вектора – косинусы углов между
вектором и ортами ПДСК:
.
a
|a|
(cos , cos , cos )
32.
.cos cos cos 1.
2
2
2
33.
П. Дано |a|=1, |b|=3, угол между ними φ=π/3.Вычислить
2a b 3a 2b .
2a b 3a 2b 6a a 4a b 3b a 2b b
2
2
6 a a b 2 b
2
2
6 a a b cos 2 b
.
6 1 1 3 cos
2
3
2 3
2
1
21
2
6 1 1 3 2 3 .
2
2
2
34. Векторное произведение векторов
Опр. Векторным произведением (cross product)векторов a и b называется вектор c,
удовлетворяющий следующим условиям:
1. c a c b
2. с a b sin(a, b)
3. {a, b, c} правая тройка векторов.
c a b или c [a,b]
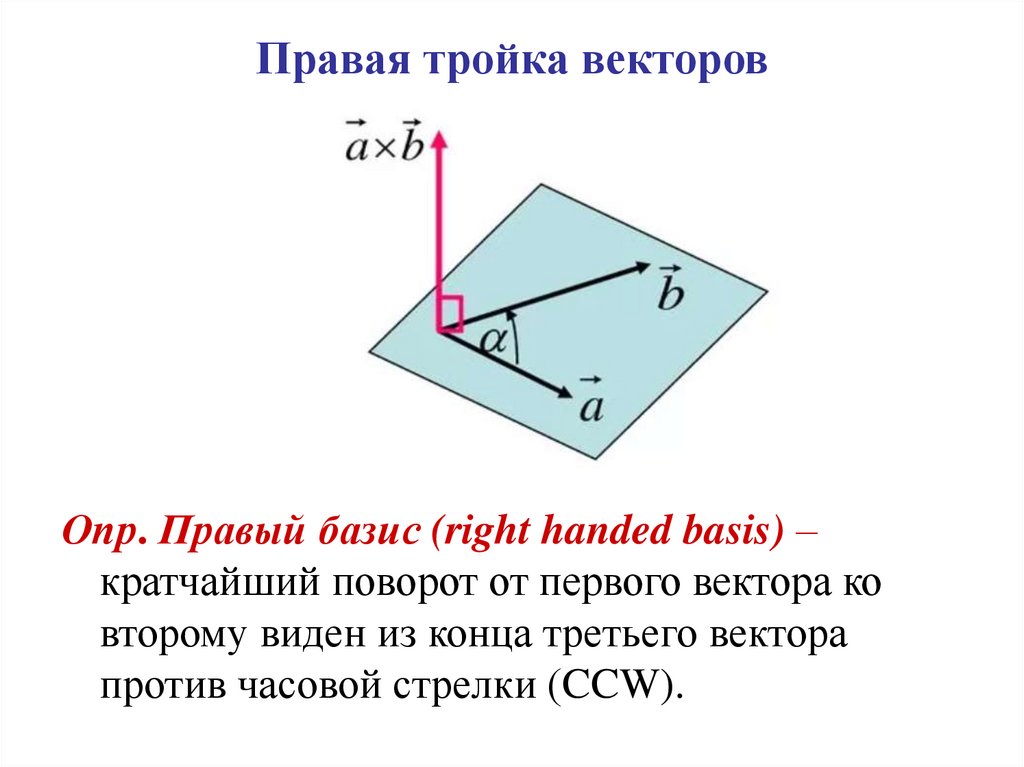
35. Правая тройка векторов
Опр. Правый базис (right handed basis) –кратчайший поворот от первого вектора ко
второму виден из конца третьего вектора
против часовой стрелки (CCW).
36. Свойства векторного произведения
1. a, b b, a ;2. a, b 0 a b a 0 b 0 ;
3. a b, c a, c b, c ;
a, b c a , b a, c ;
.
4. a, b a, b a, b , R.
Упр. Доказать свойства 1-4.
37.
Т. (выражение ВП через координаты). В ПДСКa ax i a y j a z k
b bx i by j bz k ,
тогда
i
a, b a x
bx
.
j
ay
by
k
az
bz
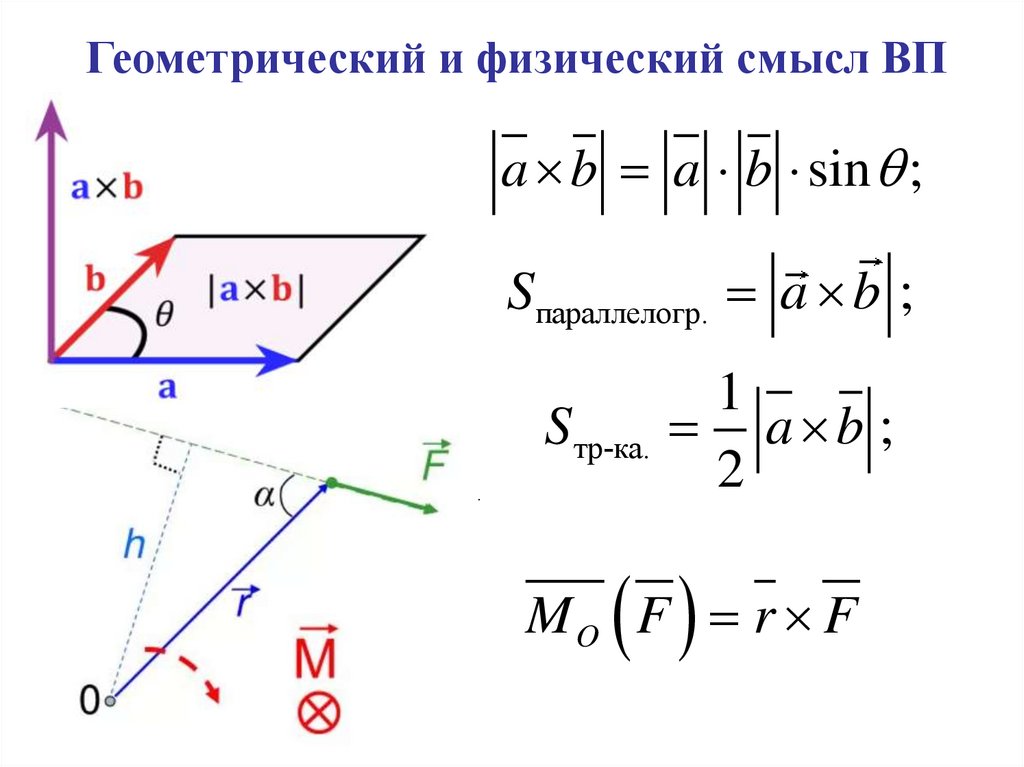
38. Геометрический и физический смысл ВП
a b a b sin ;Sпараллелогр. a b ;
.
1
S тр-ка. a b ;
2
MO F r F
39.
П. Даны координаты вершин треугольникаАВС: А (1, 1, 1), В (2, 3, 4), С (4, 3, 2). Найти его
площадь.
AB (2 1; 3 1; 4 1) (1; 2;3);
AC (3, 2, 1);
1
S ABC AB AС ;
2
i j k
.
AB AC 1 2 3
3 2 1
40.
i (2 6) j (1 9) k (2 6) ( 4, 8, 4);1
2
2
2
S ABC ( 4) 8 ( 4)
2
96
2
2 6 (ед ).
2
Упр.
.
41.
П. Найти площадь параллелограмма, построенногона векторах a+2b и 2a+b, если а и b – единичные
векторы, угол между которыми π/3.
a 2b 2a b
a 2a b 2b 2a b
2a a a b 4a b 2b b
.
0 3a b 0 3b a.
42.
S 3b a 3 b a sin3 3
2
ед .
3 1 1 sin
2
3
Упр.
.
43. Смешанное произведение векторов
Опр. Смешанным произведением (scalar tripleproduct) векторов a и b называется число:
(a ,[b , c ]).
Обозначение: (a, b, c),
abc.
Свойства смешанного произведения
1. (a, b, c) (b, c, a) (c, a, b);
2. (a, b, c) (b, a, c)
(b, c, a) (c, b, a) ...
44.
3. ( a, b, c) (a, b, c) (a, b, c);4. (a1 a2 , b, c) (a1 , b, c) (a2 , b, c);
(a, b1 b2 , c) (a, b1 , c) (a, b2 , c);
(a, b, c1 c2 ) (a, b, c1 ) (a, b2 , c2 );
a 0 b 0 c 0 .
5. a, b, c 0 a, b, c компланарны
.
Упр. Доказать свойства 1-4.
45.
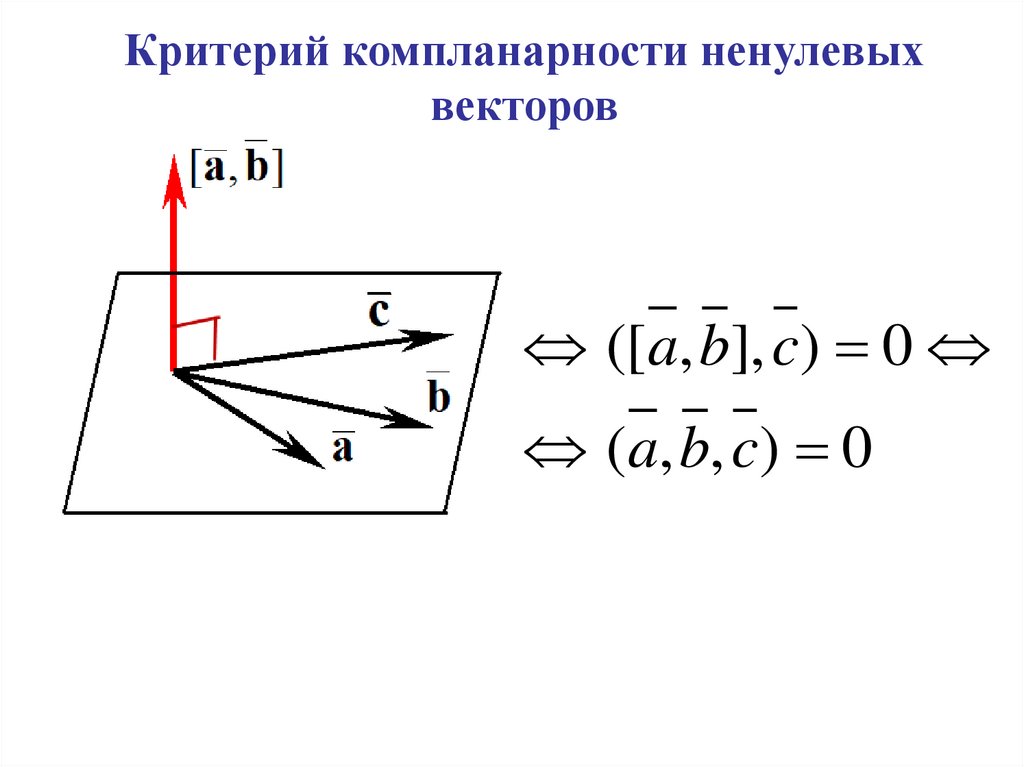
Критерий компланарности ненулевыхвекторов
([a, b], c) 0
(a, b, c) 0
.
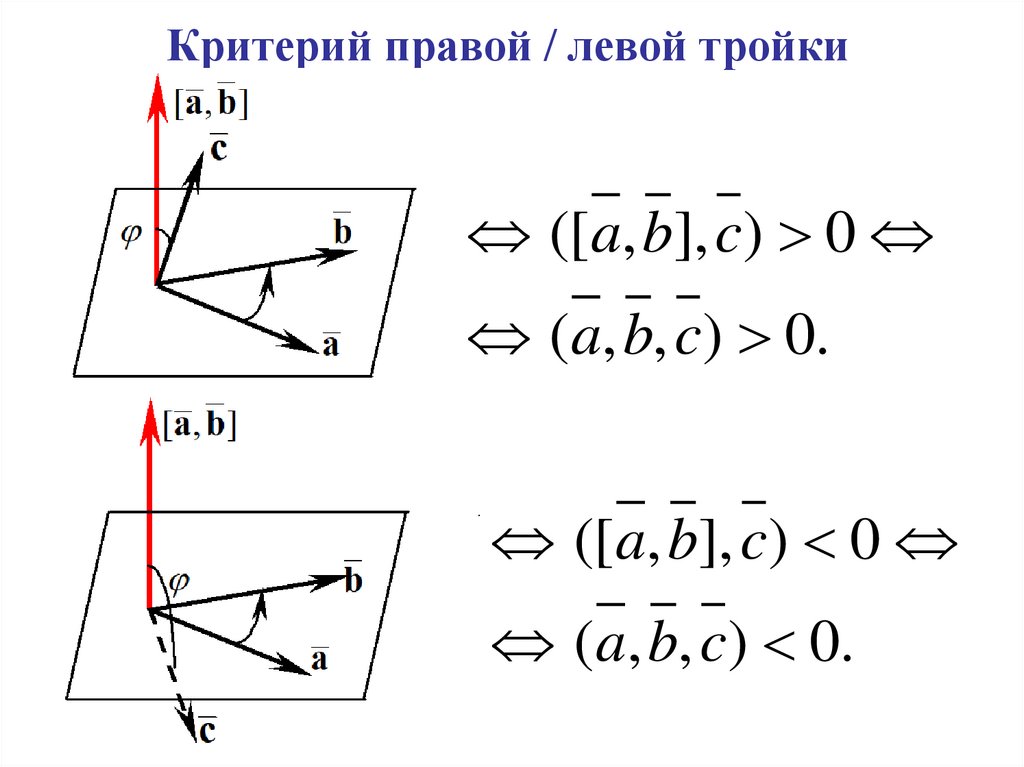
46.
Критерий правой / левой тройки([a, b], c) 0
(a, b, c) 0.
.
([a, b], c) 0
(a, b, c) 0.
47. Геометрический смысл смешанного произведения
Vпаралл да Sh[ a, b] h
.
[a, b] c cos (a, b, c) .
1
Vтетраэдра (a, b, c) .
6
48.
Т. (выражение СмП через координаты). В ПДСКax
(a, b, c) bx
cx
ay
by
cy
az
bz
cz
В любом базисе
a1
(a, b, c) b1
c1
.
a2
b2
c2
a3
b3 (e1 , e2 , e3 ).
c3
49.
Упр..












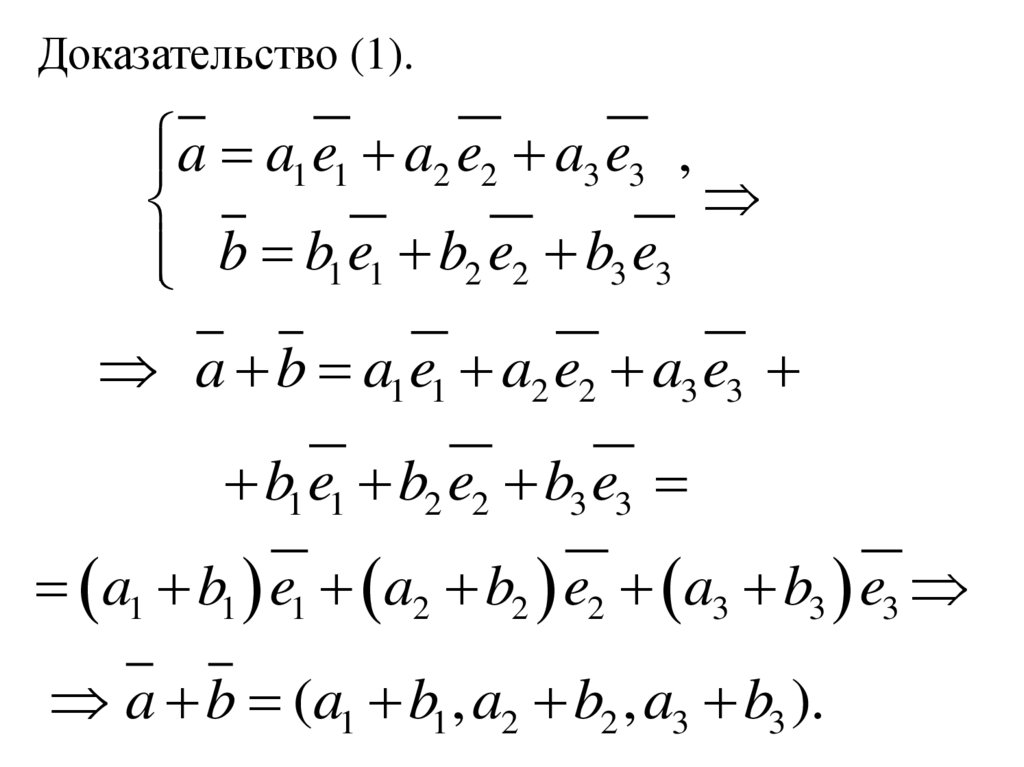












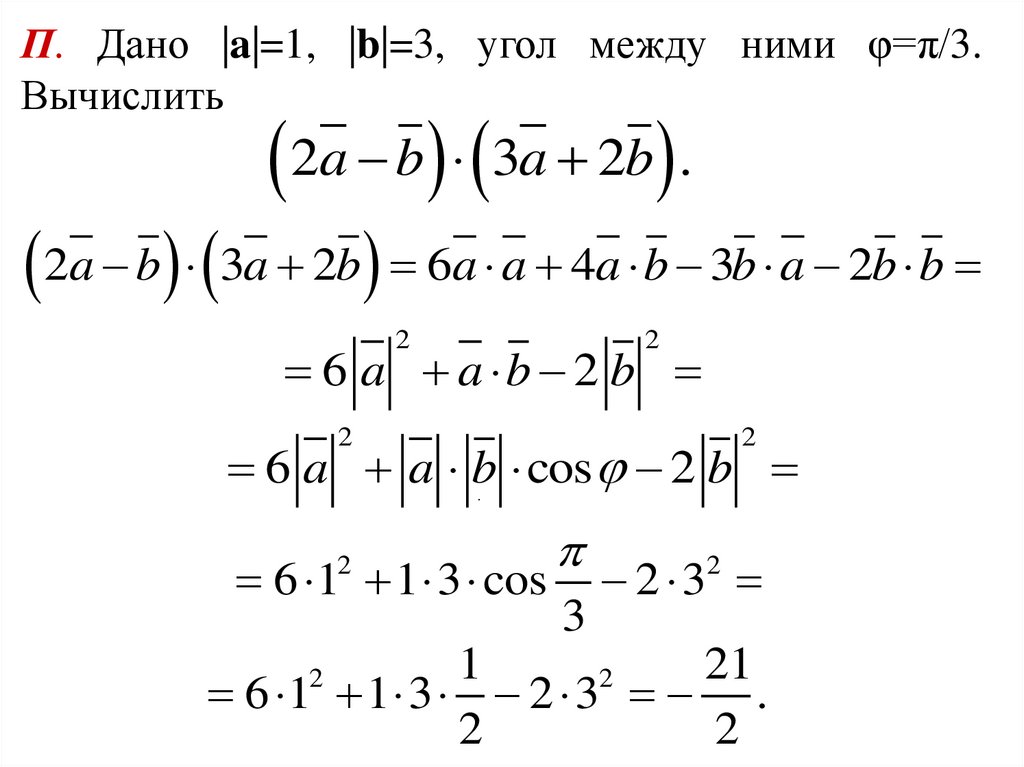








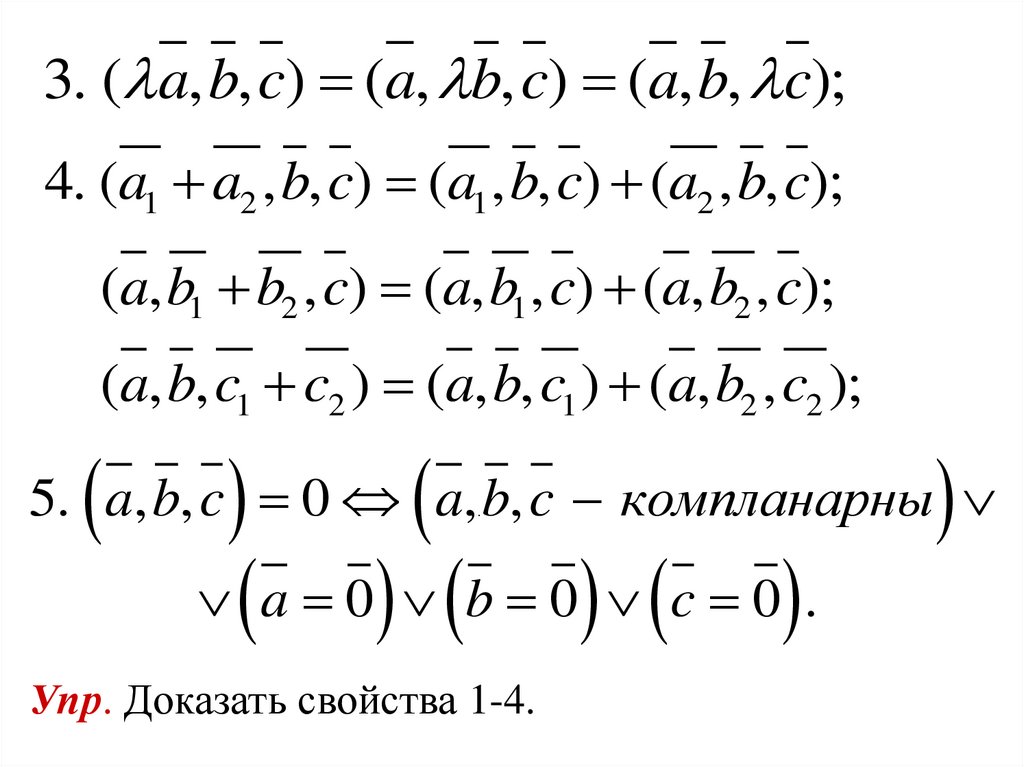



 mathematics
mathematics








