Similar presentations:
Векторы. Векторное n – мерное пространство
1. Векторы
План.1. Векторное n – мерное пространство.
2. Пространство R2 и R3.
3. Скалярное произведение векторов. Длина
вектора. Угол между векторами.
4. Плоскость в трехмерном пространстве.
5. Прямая линия в трехмерном пространстве.
6. Линейная зависимость и линейная независимость
векторов. Базис пространства Rn.
2. Векторное n – мерное пространство.
Определение. Пусть n – любоенатуральное число. Упорядоченная
совокупность n чисел a1, a2, …, an
называется n – мерным вектором.
r
r
a = (a1 , a2 , K , an ) = a (ai )n
r
a
А
uuur
AB
В
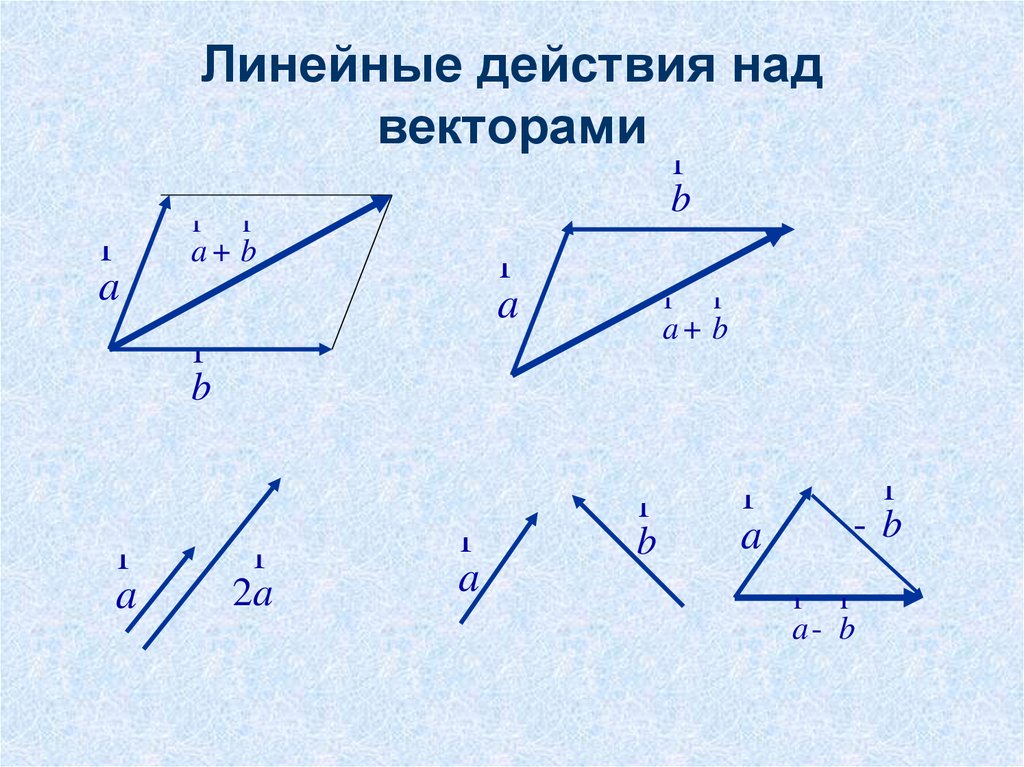
3. Линейные действия над векторами
ra
r
b
r r
a+ b
r
a
r r
a+ b
r
b
r
a
r
2a
r
a
r
b
r
a
r
-b
r r
a- b
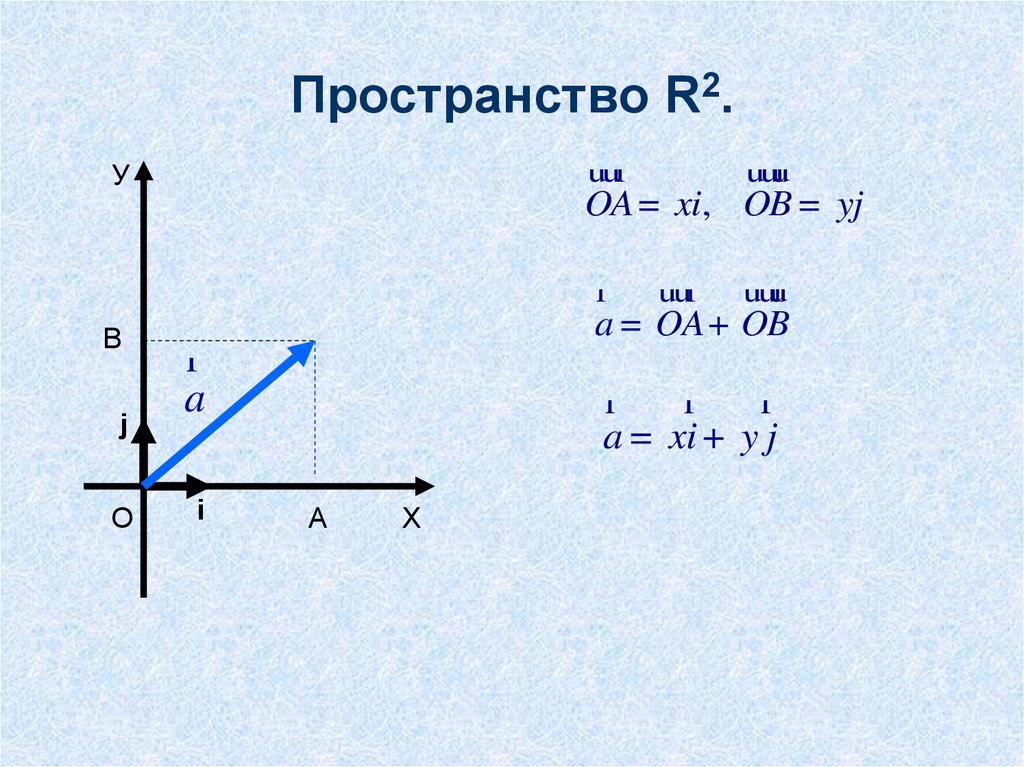
4. Пространство R2.
uuruuur
OA = xi, OB = yj
У
B
j
О
r uur uuur
a = OA + OB
r
a
i
r
r
r
a = xi + y j
A
Х
5. Пространство R3.
Zk
i
O
r
a=
r
a=
r
a
C
j
Y
A
X
B
uur uuur uuur
OA + OB + BC
r
r
r
xi + y j + zk
6. Скалярное произведение векторов
r r r ra Чb = a Чb cosj , 0 Ј j Ј p
r r
a Чb
cos j = r r
a Чb
r
r
a = (a1; a2 , a3 ), b = (b1 , b2 , b3 )
r r
a Чb = a1b1 + a2b2 + a3b3
cos j =
ur ur uur ur ur ur
a1 Чb1 + a2 Чb2 + a3 Чb3
a12 + a22 + a32 Ч b12 + b22 + b32
7. Направляющие косинусы
Zr
a
cos a =
g
О
a
X
cos b =
b
Y
cos g =
a1
a12 + a22 + a32
a2
a12 + a22 + a32
a3
a12 + a22 + a32
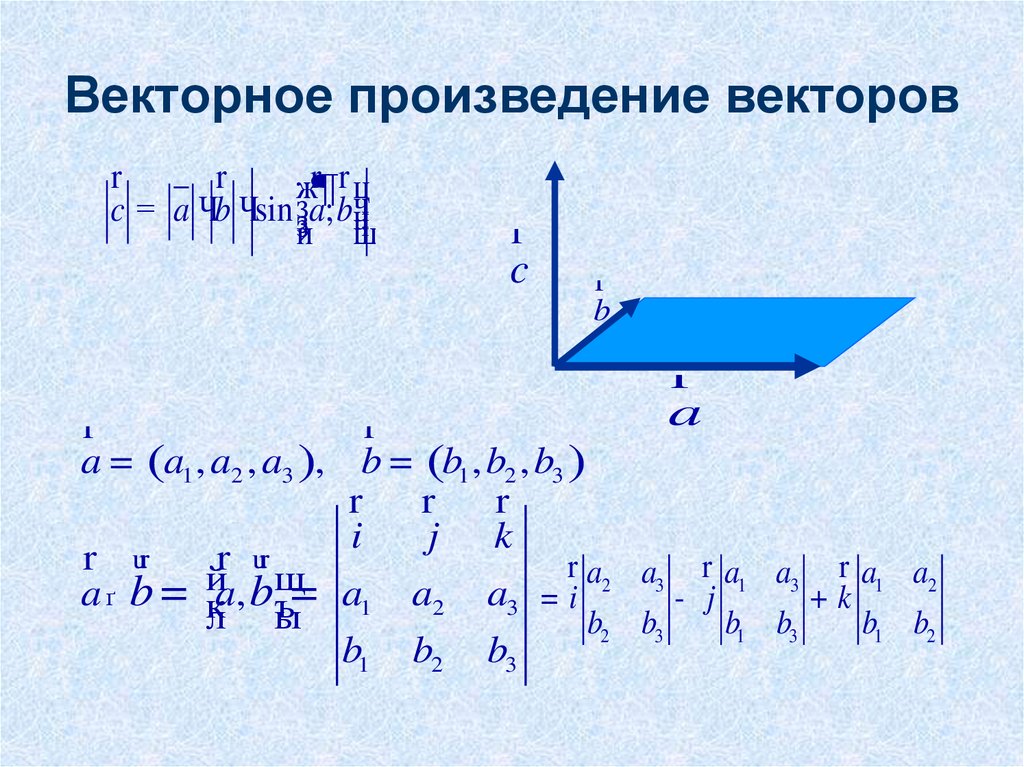
8. Векторное произведение векторов
rr
жr¶r цч
c = a Чb Чsin ззa; bчч
и ш
r
c
r
b
r
a
r
r
a = (a1 , a2 , a3 ), b = (b1 , b2 , b3 )
r
r
r
i
j k
u
r
u
r
r
r
r a2 a3 r a1 a3 r a1 a2
й
щ
a ґ b = кa, bъ= a1 a2 a3 = i
- j
+k
л ы
b2 b3
b1 b3
b1 b2
b1 b2 b3
9. Свойства векторного произведения
rrйa bщ= 0 - условие коллинеарности
к
ъ
л ы
0
1
20
rr
rr
йabщ= - йb a щ
к
л ъ
ы к
л ъ
ы
3
rr
й
щ=
m Чкa bъ
л ы
40
rr
йa bщ=
кл ы
ъ
ur r
йa / bщ
к ъ
л ы
0
йar + br
кл
rщ
c ъ=
ы
0
5
(
)
йmar
кл
rщ
bъ=
ы
( )
rr
йa c щ+
кл ъ
ы
йar mbr щ
кл
ъ
ы
( )
rr
йb c щ
кл ъ
ы
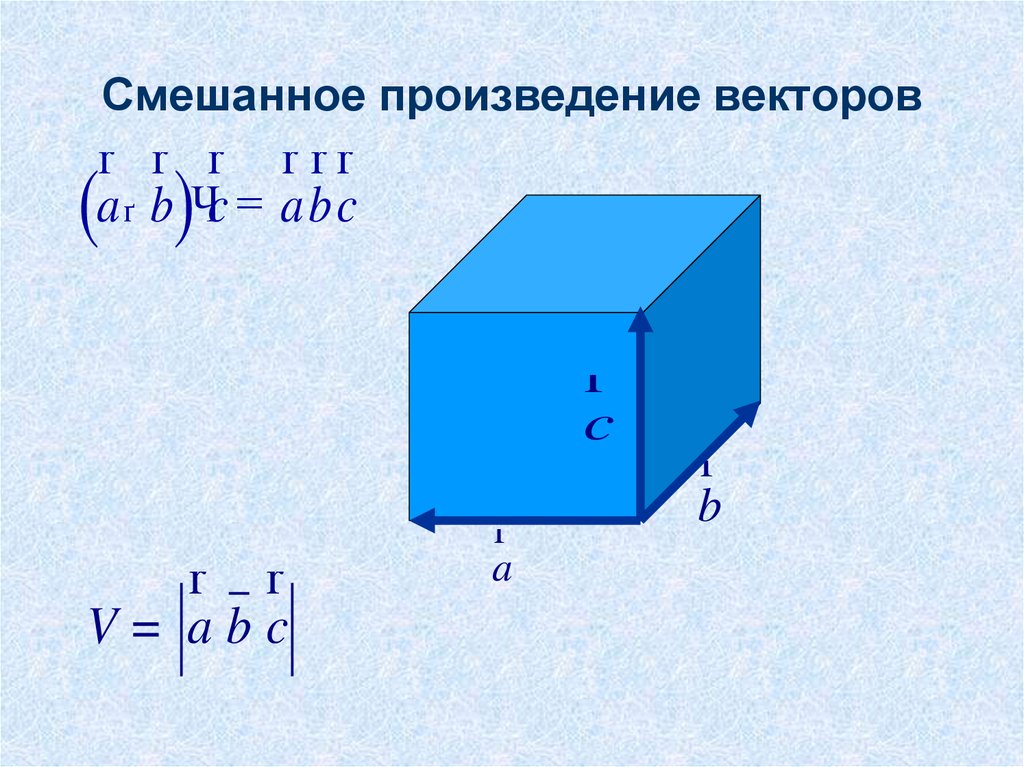
10. Смешанное произведение векторов
r r r rrra ґ b Чc = abc
( )
r
c
r r
V= abc
r
a
r
b
11. Свойства смешанного произведения
rr rr
r
r
йabщc < 0
щc > 0
10 й
a
b
к
кл ы
ъ
л ъ
ы
r
r
r
c r
c a
b
r
b
20
30
r
a
rr r
rr r
rr r rrr
йabщc = йbcщa = йc aщb = abc
к
л ъ
ы к
л ъ
ы к
л ъ
ы
rrr
abc = 0 - условие компланарности
12. Поверхность в трехмерном пространстве
Zf (x; y; z )= 0
Y
X
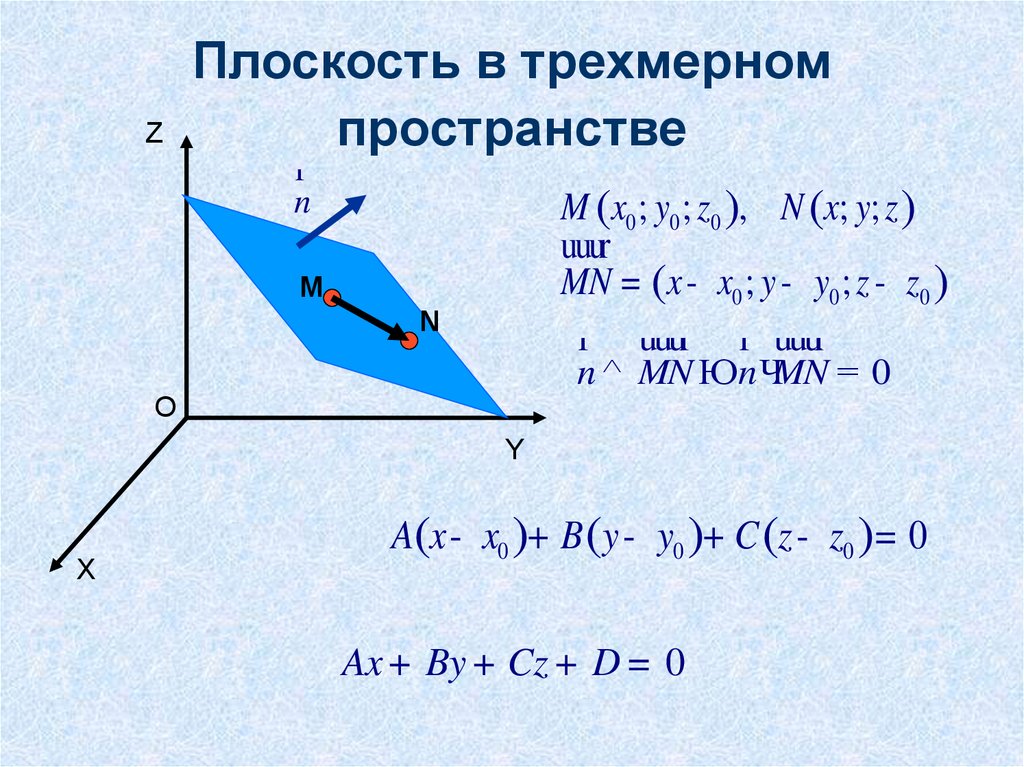
13. Плоскость в трехмерном пространстве
ZПлоскость в трехмерном
пространстве
r
n
M (x0 ; y0 ; z0 ), N (x; y; z )
uuur
MN = (x - x0 ; y - y0 ; z - z0 )
M
N
r uuur r uuur
n ^ MN Юn ЧMN = 0
O
Y
X
A(x - x0 )+ B (y - y0 )+ C (z - z0 )= 0
Ax + By + Cz + D = 0
14. Прямая линия в трехмерном пространстве
Zur
p
M (x0 ; y0 ; z0 ), N (x; y; z ), N1 (x1; y1; z1 )
ur
p (l; m; n)
N
uuur
MN = (x - x0 ; y - y0 ; z - z0 )
М
N1
О
У
Х
uuur
ur
MN = t p
(x - x0 ; y - y0 ; z - z0 )= (tl; tm; tn)
x - x0 = tl , y - y0 = tm, z - z0 = tn
x = x0 + tl , y = y0 + tm, z = z0 + tn
15. Прямая линия в трехмерном пространстве
2)uur
p0 (cos a ; cos b ; cos g )
x = x0 + t cos a ,
y = y0 + t cos b ,
x - x0
y - y0
3)
= t,
= t,
l
m
x - x0
y - y0 z - z 0
=
=
l
m
n
z - z0
= t,
n
z = z0 + t cos g










 mathematics
mathematics








