2.06M

Category: $mathematics$ mathematics

272650 - 108 слайдов Интегральное исчисление

1.

Финансовый университет
при Правительстве Российской Федерации
Тема №6.
Интегральное исчисление

2.

Функция F (x ) называется первообразной
функцией для функции f (x ) на множестве
Х, если в каждой точке х этого множества
справедливо равенство
F ' ( x) f ( x).

Задача
Например:
x является первообразной для 3x
3
2
x 3 1 тоже первообразная для 3x 2 .
Т.о. всякая непрерывная функция имеет
бесконечное множество первообразных,
которые отличаются друг от друга
постоянным слагаемым.

4.

Совокупность всех первообразных для
функции f (x ) на множестве Х называется
её неопределённым интегралом и
обозначается
f ( x)dx.
f ( x) подынтегральная функция
f ( x)dx подынтегральное выражение
x выражение, стоящее под знаком
дифференциала

5.

Свойства неопределённого интеграла
1. Производная неопределённого интеграла
равна подынтегральной функции, а его
дифференциал равен подынтегральному
выражению;
2. Неопределённый интеграл от
дифференциала с точностью до
постоянного слагаемого равен
выражению, стоящему под знаком
дифференциала
d [ f ( x)] f ( x) C;

6.

Свойства неопределённого интеграла
3. Постоянный множитель можно выносить
за знак интеграла
k
f
(
x
)
dx
k
f
(
x
)
dx
;
4. Неопределённый интеграл
алгебраической суммы конечного числа
слагаемых равен алгебраической сумме
интегралов этих слагаемых
f ( x) g ( x) ( x) dx
f ( x ) dx g ( x ) dx ( x ) dx;

7.

Свойства неопределённого интеграла
5. Об инвариантности формул
интегрирования. Всякая формула
интегрирования сохраняет свой вид при
подстановке вместо независимой
переменной любой дифференцируемой
от неё функции
f ( x)dx F ( x) C f (u )du F (u ) C ,
u (x) дифференцируема по х.

8.

Задача
Например:
3x dx x C;
3 sin x d (sin x) sin x C.
2
3
2
3

9.

Основные формулы интегрирования
n 1
x
1. x dx
C , (n 1)
n 1
dx x C
n
dx
2.
ln x C
x
x
a
x
3. a dx
C
ln a
x
x
e
dx
e
C

10.

Основные формулы интегрирования
4. cos xdx sin x C
sin xdx cos x C
dx
cos 2 x tgx C
dx
sin 2 x ctgx C

11.

Основные формулы интегрирования
5.
dx
x
arcsin C
a
a2 x2
dx
1
x
6. 2
arctg C
2
a x
a
a
dx
7.
ln x x 2 a C
2
x a
dx
1
x a
8. 2
ln
C
2
x a
2a x a

12.

Интегрирование
Рассмотрим некоторые из основных методов
интегрирования.
1. Метод разложения интеграла в сумму
интегралов
f ( x) g ( x) ( x) dx
f ( x ) dx g ( x ) dx ( x ) dx

13.

Задача
Пример. Найти
3 x
2
3
5
x
3
dx.
5
2
3
x
x
x 2

14.

Задача
Решение:
3 x
2
3
5
x
3
dx
5
2
3
x
x
x 2
5
3
dx
dx
x dx 3 dx 2 x dx 3 x 5 x 2 2
3
4
x
x
2
3
x
3
x
2
2
3 ln x 5 ln x x 2 C.
2
4 ln 3
3

15.

Задача
Пример. Найти
x 2 dx.
3
x2

16.

Задача
Пример. Найти
x 2 dx.
3
x2
Решение: x 2 dx
x 3 6 x 2 12 x 8
dx
2
x2
x
x 3 6 x 2 12 x 8
2 2 2 2 dx
x
x
x
x
3
dx
2
x dx 6 dx 12 8 x dx
x
x2
8
6 x 12 ln x C.
2
x

17.

Задача
Пример. Найти
2 2 dx.
x
x 2

18.

Задача
Пример. Найти
2 2 dx.
x 2
x
Решение:
2 2 dx 2 2 2 2 2 dx
x 2
x
x 2
2 dx 2dx 2
2x
2 x
x
x
x 2
x
1
dx 4 dx 2 dx dx
4
x
x
x
4
1
1
4
4
2 x : ln C
2 x C.
ln 4
4
ln 4
4
x
x

19.

Задача
2. Метод замены переменной. Метод
внесения функции под знак дифференциала.
Пример. Найти
4 3x dx.

20.

Задача
Решение.
4 y
4 3x y x
3 3
4 3x dx
dy
dx
3
1, 5
dy
1
1
y
0,5
y y dy
C
3
3 1,5
3
2
3
4 3 x C.
9

21.

Задача
dx
Пример. Найти
x ln x

22.

Задача
dx
Пример. Найти
x ln x
Решение:
dx
y
y
x ln x ln x y x e dx e dy
e y dy
dy
y
ln y C ln ln x C.
e y
y

23.

Задача
Можно использовать вместо замены
переменной метод внесения функции под знак
'
дифференциала, используя: y dx dy.
Решение:
dx
x 1dx
(ln x) ' dx
d (ln x)
x ln x ln x ln x ln x ln ln x C.

24.

Задача
Некоторые другие примеры внесения под
знак дифференциала:
dx
2
d (2 x ), xdx d (0,5 x ),
x
dx
d (arcsin x), e x dx d (e x ).
1 x2

25.

Задача
Получение линейной функции:
d (ax b) d (ax) db adx
1
dx d (ax b).
a

26.

Задача
Пример: Найти
dx
(2 5 x)
5
3

27.

Задача
dx
(2 5 x)
Решение:
5
3
5
3
3
5
1
(2 5 x) dx (2 5 x) d (2 5 x)
5
0, 4
(2 5 x)
0, 4
0,2
C 0,5 (2 5 x) C.
0,4

28.

Задача
Решение 1-го примера из этого типа:
1
0,5
4 3x dx 3 (4 3x) d (4 3x)
1 (4 3 x)1,5
2
3
4 3 x C.
3
1,5
9

29.

Задача
Пример. Найти
e
x 2
x
dx.

30.

Задача
Решение:
e
2 e
x 2
x
dx e
x 2
x 2
d (2 x )
d ( x 2) 2e
x 2
C.

31.

Задача
Пример. Найти
dx
x 1 3
Решение:
x 1 3 y x 1 ( y 3)
dx
x 1 3 x y 2 6 y 10 dx 2 y 6 dy
2
2y 6
dy
dy 2 dy 6
2 y 6 ln y C
y
y
2 x 1 3 6 ln x 1 3 C.

32.

Задача
Пример. Найти
x
3
dx
.
x2

33.

Задача
Пример. Найти
x
3
dx
.
x2
Решение:
dy
x 3 dx x y x y dx 2 y
x2
2
y
x2
dy
1 y
3
3
y 3
3 dy
C
C.
2 ln 3
2 ln 3
2 y 2
y

34.

Задача
или:
2
x
x
x
x2
2
x
3
dx
3
d
0
,
5
3
d
(
x
)
2
2
x2
3
C.
2 ln 3
2

35.

Интегрирование
3. Метод интегрирования по частям.
d (uv) du v u dv
d (uv) v du u dv
u dv u v v du
Формула интегрирования по частям.

36.

Задача
Пример. Найти
3x 5 ln x dx

37.

Задача
Пример. Найти
Решение:
3x 5 ln x dx
3x 5 ln x dx
dx
u ln x du
x
2
3x
dv (3 x 5)dx v
5x
2
3x 2
3x 2
dx 3 x 2
ln x
5 x
5 x
5 x ln x
2
2
x 2
2
2
3
x
3
x
3
x
5 dx
5 x ln x
5 x C .
2
2
4

38.

Задача
Пример. Найти
Решение:
x 3x e dx
2
4x

39.

Задача
x 3x e dx
u x 2 3x du 2 x 3 dx
4x
4x
e
e
dv e 4 x dx
d 4 x v
4
4
4x
4x
e
e
x 2 3x
2 x 3
dx
4
4
2x 3 2x 3
u
du 0,5dx
4x
e
4
4 4
2
x
3x
4x
4
e
4x
dv e dx v
4
2x 3 4x 1 4x
x 2 3x 4 x 2 x 3 4 x 1 4 x
e e dx
e
e e C
16
8
4
16
32
2
4x

40.

Интегрирование
4. Интегрирование функций вида:
a1 x b1
;
2
a2 x b2 x c2
a1 x b1
a2 x 2 b2 x c2
.

41.

Интегрирование
1. В числителе дроби выделить производную
a2 x 2 b2 x c2 ;
2. Разложить подынтегральную функцию на
два слагаемых;
3. Один из интегралов (первый) решается
заменой или внесением под знак
дифференциала, другой выделением полного
квадрата в знаменателе.

42.

Задача
Пример. Найти
3 x 15
x 2 4 x 20dx.

43.

Задача
Решение:
3x 15
x 5
x 2 4 x 20dx 3 x 2 4 x 20dx
3 2 x 10
3 2x 4 6
dx 2
dx
2
2 x 4 x 20
2 x 4 x 20
3
2x 4
dx
dx 9 2
2
2 x 4 x 20
x 4 x 20
3 d ( x 2 4 x 20)
dx
9
2
2
2
x 4 x 20
( x 2) 16
9
x 2
2
1,5 ln x 4 x 20 arctg
C.
4
4

44.

Задача
Пример. Найти
dx
6 4x 2x .
2

45.

Задача
Решение:
dx
1
dx
2
6 4x 2x2
( x 2 2 x 3)
1
dx
1
d ( x 1)
2
2
(( x 1) 2 4)
4 ( x 1) 2
1
x 1
arcsin
С.
2
2

46.

Интегрирование
5. Интегрирование дробно-рациональных
функций.
Сначала выделить целую часть дроби (если
эта дробь неправильная, у которой степень
числителя больше или равна степени
знаменателя). Затем разложить дробь в сумму
простейших дробей (у которых знаменатель
не раскладывается на рациональные
множители). Применить «метод
неопределённых коэффициентов».

47.

Интегрирование
Разложение дробей в простейшие:
1. Корни знаменателя действительные и
различные:
P( x)
A
B
C
( x x1 )( x x2 )( x x3 ) x x1 x x2 x x3
2. Корни знаменателя кратные:
P( x)
A
B
C
3
3
2
( x x0 )
( x x0 ) ( x x0 )
x x0

48.

Интегрирование
3. В знаменателе имеются комплексные корни:
P( x)
A
Bx C
2
2
( x x0 )( ax bx c) x x0 ax bx c

49.

Задача
Пример. Найти
2x2 1
x3 3x 2dx

50.

Задача
Решение:
2x2 1
2x2 1
2x2 1
3
3
2
x 3x 2 x 3x 3 1 ( x 1)( x x 1) 3( x 1)
2x2 1
2x2 1
2x2 1
2
2
( x 1)( x x 2) ( x 1)( x 1)( x 2) ( x 1) ( x 2)
A
B
C
2
( x 1)
x 1 x 2
A( x 2) B( x 1)( x 2) C ( x 1) 2
( x 1) 2 ( x 2)

51.

Задача
2 x 1 A( x 2) B( x 2)( x 1) C ( x 1)
2
2
2 x 2 1 Ax 2 A Bx 2 Bx 2 B Cx 2 2Cx C
B C 2
A B 2C 0
2 A 2 B C 1

52.

Задача
1
11
7
A ; B ;C
3
9
9
2x2 1
1
11
7
2
2
( x 1) ( x 2) 3( x 1) 9( x 1) 9( x 2)

53.

Задача
2x2 1
1
dx
11 dx
x 3 3x 2dx 3 ( x 1) 2 9 x 1
7 dx
1
11
7
ln x 1 ln x 2 C
9 x 2
3( x 1) 9
9

54.

Задача
Пример. Найти
3x
x3 1dx

55.

Задача
Решение:
3x
3x
A
Bx C
2
3
2
x 1 ( x 1)( x x 1) x 1 x x 1

56.

Задача
Решение:
3x
3x
A
Bx C
2
3
2
x 1 ( x 1)( x x 1) x 1 x x 1
A( x x 1) ( Bx C )( x 1) 3x
2
A B 0
B A
A 1
A B C 3 C A B 1
A C 0
3 A 3 C 1

57.

Задача
3x
dx
x 1
x 3 1dx x 1 x 2 x 1dx.
x 1
1 2x 1 3
x 2 x 1dx 2 x 2 x 1dx
1
2x 1
3
dx
2
dx 2
2 x x 1
2 x x 1
2
1 d ( x x 1) 3
dx
2
2
2
x x 1
2 ( x 0,5) 0,75

58.

Задача
1
3
1
x 0,5
2
ln x x 1
arctg
C
2
2 0,75
0,75
1
2x 1
2
ln( x x 1) 3 arctg
C.
2
3
2x 1
Ответ : ln x 1 ln x x 1 3 arctg
С.
3
2

59.

Интегрирование
6. Тригонометрические подстановки.
В интегралах, содержащих sin x; cos x
Можно использовать тангенсную подстановку:
x
2dt
t tg x 2 arctg t dx
,
2
2
1 t
2
2t
1 t
sin x
, cos x
.
2
2
1 t
1 t

60.

Задача
Пример. Найти
dx
2 sin x cos x 1

61.

Задача
Решение:
dx
2 sin x cos x 1
2dt
2
4
t
1
t
2
(1 t )
1
2
2
1 t 1 t
2dt
dt
d (t 1)
2
2
2
2
4t 1 t 1 t
t 2t
(t 1) 1
1 t 1 1
1 tg (0,5 x) 2
ln
C C ln
2 t 1 1
2
tg (0,5 x)

62.

Задача
Пример. Найти
1 x dx
2

63.

Задача
Решение:
x sin t
1 x dx
1 sin 2 t cos t dt
dx cos t dt
2
cos 2 t dt 0,5 (1 cos 2t )dt 0,5 dt
0,25 cos 2t d (2t ) 0,5t 0,25 sin 2t C
0,5 arcsin x 0,5 sin(arcsin x) cos(arcsin x) C
0,5 arcsin x 0,5 x 1 x C.
2

64.

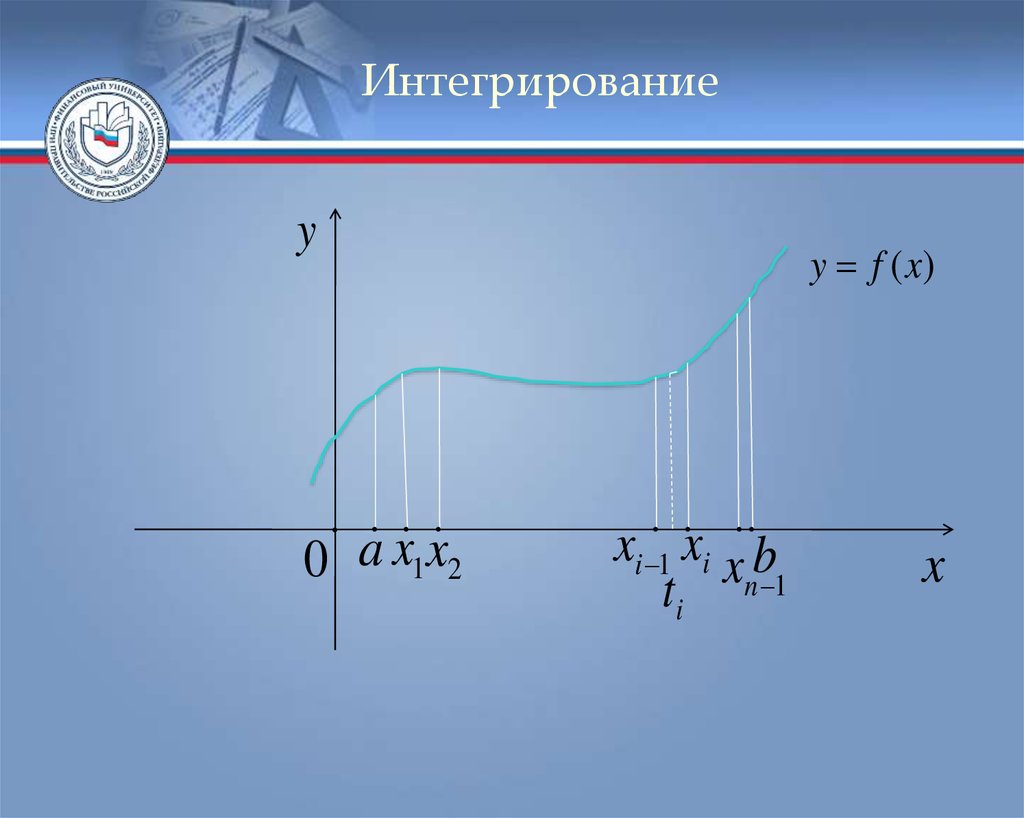
Интегрирование
Рассмотрим задачу о вычислении площади
криволинейной трапеции: Пусть на отрезке
[a; b] задана неотрицательная функция y f (x ).
Найдём площадь криволинейной трапеции,
ограниченной линиями: y f ( x), y 0, x a, x b.
Разобьём отрезок на n частичных интервалов
точками x1 , x2 , ... , xn 1. Обозначим xi xi 1 xi .
На каждом из полученных интервалов
выберем некоторую точку ti .
Si f (ti ) xi
n
S S1 ... S n f (ti ) xi
i 1

65.

Интегрирование
y
y f (x)
x
0 a 1 x2
xi 1 x i x b
ti n 1
x

66.

Интегрирование
Сумма такого вида называется интегральной
суммой для функции y f (x) на отрезке [a; b].
Пусть существует конечный предел
интегральной суммы, который не зависит от
способа выбора точек xi , ti при стремлении к
нулю длины наибольшего частичного
интервала, тогда этот предел называется
определённым интегралом (по Риману) от
функции y f (x) на отрезке [a; b].

67.

Интегрирование
b
f
(
x
)
dx
lim
a
max xi 0
n
f (t ) x .
i 1
i
i
При этом число a называется нижним, число
b – верхним пределами интегрирования
соответственно.

68.

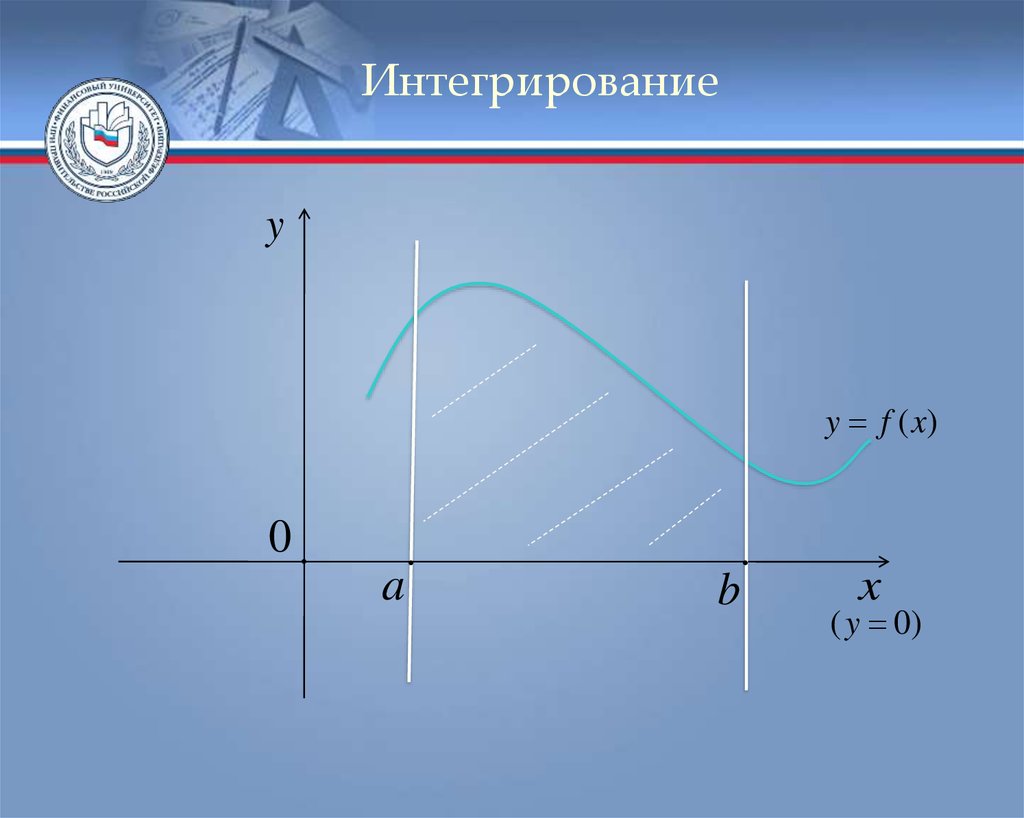
Интегрирование
Геометрический смысл определённого
интеграла. Если функция y f (x)
непрерывна и неотрицательна на отрезке [a; b],
b
То f ( x)dx численно равен площади
a
криволинейной трапеции , ограниченной
линиями y f ( x), y 0, x a, x b.

69.

Интегрирование
y
y f (x)
0
a
b
x
( y 0)

70.

Интегрирование
Теорема (достаточное условие
интегрируемости функции): Если функция
непрерывна на некотором отрезке, то она на
этом отрезке интегрируема (т.е. существует её
определённый интеграл).

71.

Интегрирование
Свойства определённого интеграла.
1. Если верхний и нижний пределы
интегрирования совпадают, то интеграл
равен нулю.
2. Если верхний и нижний пределы
интегрирования поменять местами, то
изменится знак интеграла.
3. Постоянный множитель можно выносить
за знак интеграла.
4. Интеграл алгебраической суммы конечного
числа слагаемых равен алгебраической
сумме интегралов этих слагаемых.

72.

Интегрирование
5.
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx, c [a; b].
6. Если верхний предел интегрирования
больше нижнего и подынтегральная функция
знакопостоянна, то определённый интеграл
имеет тот же знак, что и функция.
7. Если верхний предел интегрирования
больше нижнего и b
b
f ( x) g ( x), то f ( x)dx g ( x)dx.
a
a

73.

Интегрирование
8. Если верхний предел интегрирования
больше нижнего и
b
m f ( x) M , то m(b a) f ( x)dx M (b a),
a
где m и M – некоторые числа.

74.

Интегрирование
9. (Теорема о среднем) Если верхний предел
интегрирования больше нижнего и
подынтегральная функция непрерывна на
отрезке интегрирования, то внутри этого
отрезка найдётся такая точка с, для которой
справедливо равенство:
b
f ( x)dx f (c) (b a).
a

75.

Интегрирование
x
Интеграл вида
f ( x)dx называется
a
интегралом с переменным верхним пределом.
Теорема: Пусть функция непрерывна на
некотором отрезке. Тогда в каждой точке х
этого отрезка производная интеграла с
переменным верхним пределом этой функции
по её верхнему пределу равна
подынтегральной функции.

76.

Интегрирование
Теорема. Пусть функция y f (x)
непрерывна на отрезке [a; b] и F(x) – любая её
первообразная для f (x) на этом отрезке.
Тогда определённый интеграл от этой
функции равен приращению первообразной
на этом отрезке.
b
f ( x)dx F ( x) F (b) F (a)
b
a
a
Это формула Ньютона – Лейбница.

77.

Интегрирование
Теорема. Пусть функция g (t ) имеет
непрерывную производную на отрезке [c; d],
a=g(c), b=g(d) и функция f (x ) непрерывна в
каждой точке х вида х= g(t), где t принадлежит
отрезку [c; d]. Тогда справедливо равенство:
b
d
f ( x)dx f ( g (t )) g (t )dt.
'
a
c
Эта формула называется формулой замены
переменной в определённом интеграле.

78.

Интегрирование
Теорема. Пусть функции u=u(x), v=v(x)
имеют непрерывные производные на отрезке
[a; b]. Тогда
b
b
udv uv vdu.
b
a
a
a
Эта формула называется формулой
интегрирования по частям в определённом
интеграле.

79.

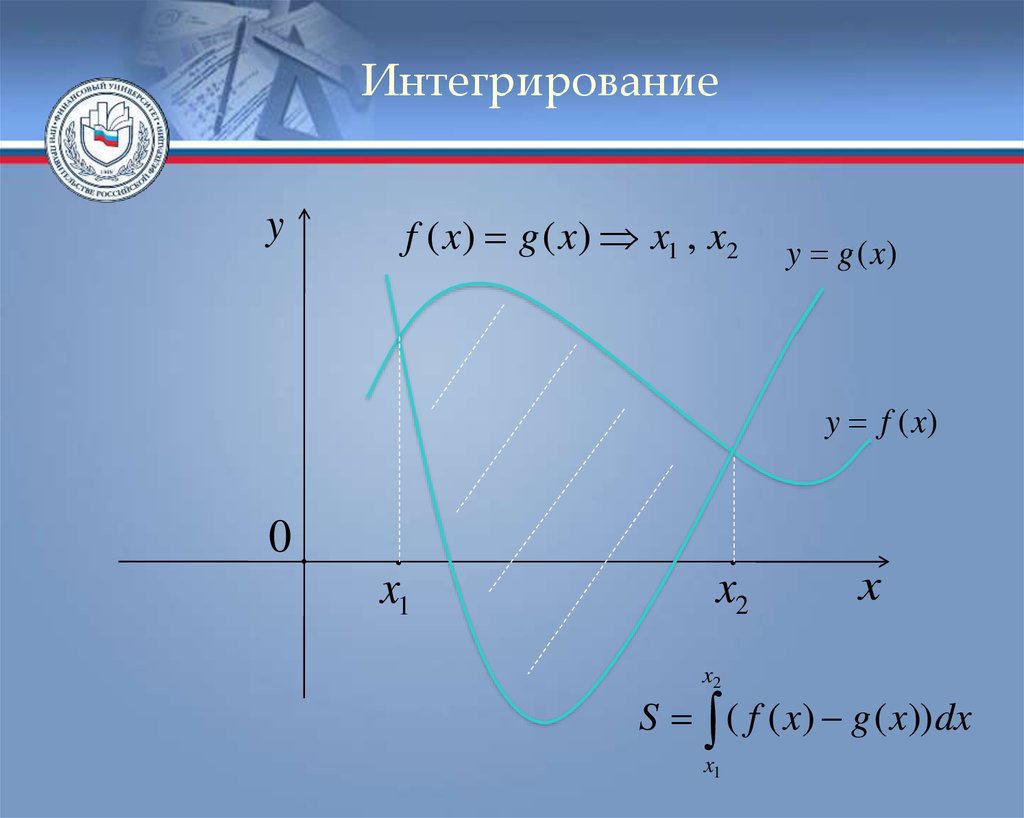
Интегрирование
y
f ( x) g ( x) x1 , x2
y g (x)
y f (x)
0
x1
x2
x2
x
S ( f ( x) g ( x)) dx
x1

80.

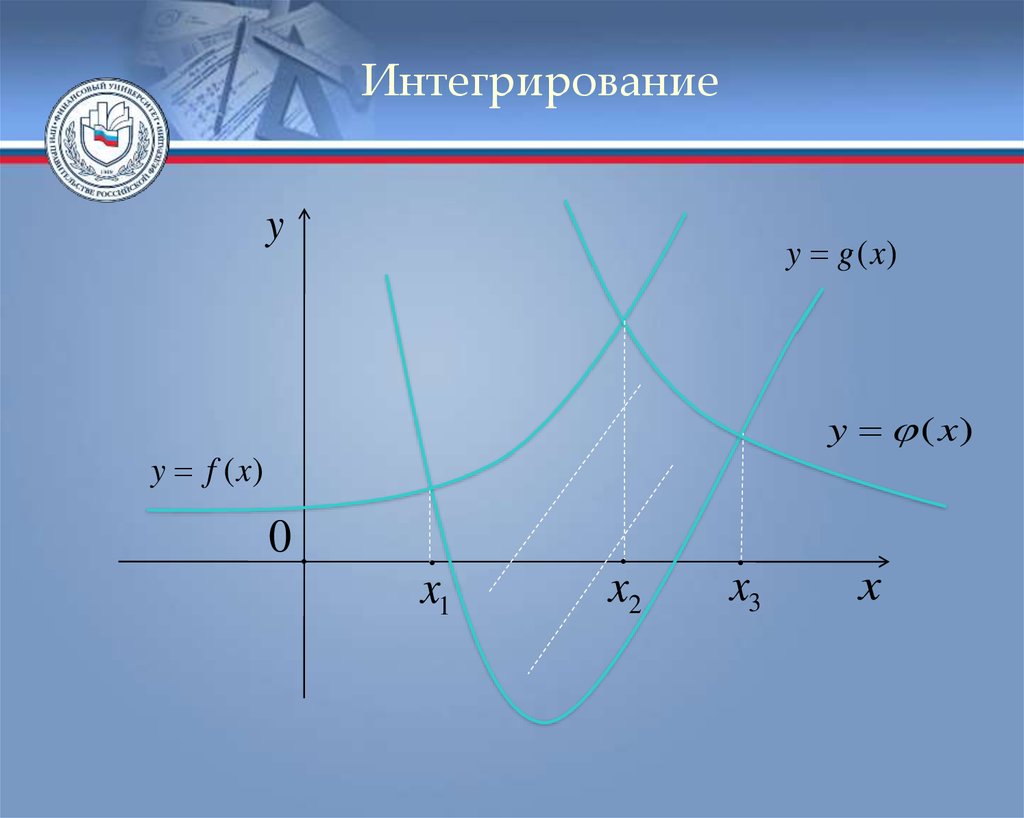
Интегрирование
y
y g (x)
y (x )
y f (x)
0
x1
x2
x3
x

81.

Интегрирование
f ( x) g ( x) x1
f ( x ) ( x ) x2
g ( x ) ( x) x3
x2
x3
x1
x2
S ( f ( x) g ( x)) dx ( ( x) g ( x)) dx

82.

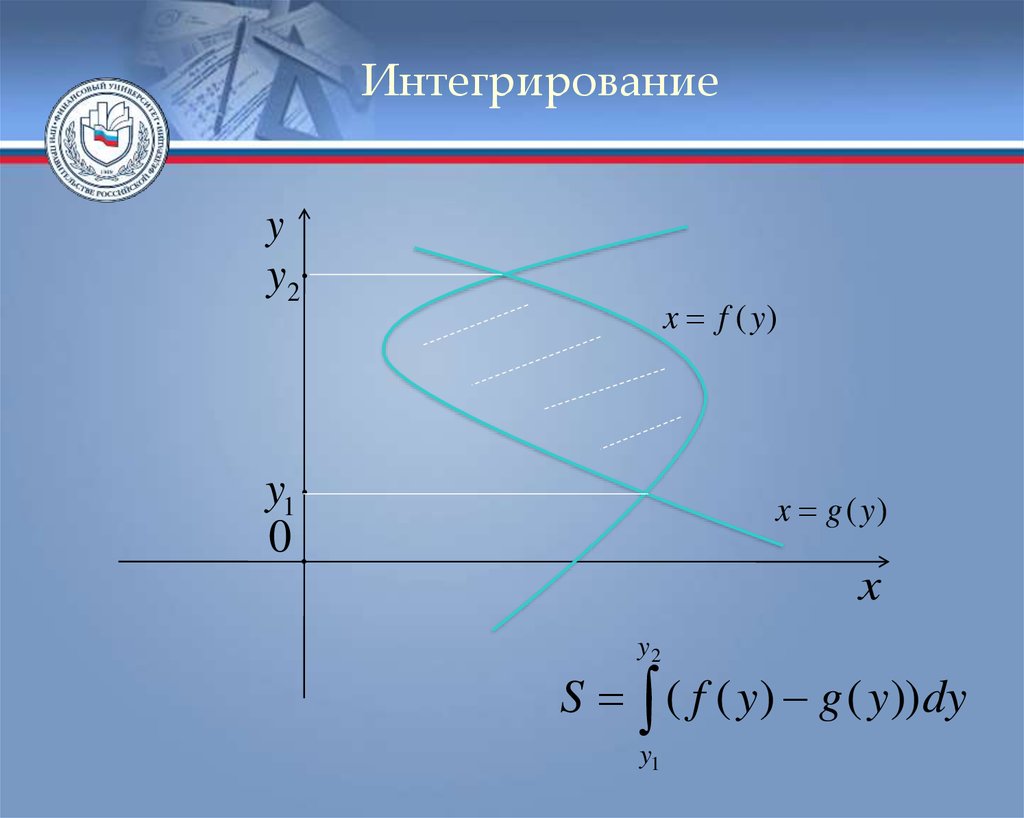
Интегрирование
y
y2
x f ( y)
y1
0
x g ( y)
x
y2
S ( f ( y ) g ( y )) dy
y1

83.

Интегрирование
С помощью определённого интеграла
можно находить площади плоских фигур,
объёмы тел вращения, объёмы тел,
полученных сечением плоскостями, площади
поверхностей, длины дуг линий, центр масс
фигур (в физике) и т.д. Рассмотрим некоторые
из этих задач.

84.

Задача
Пример. Найти площадь фигуры,
ограниченной линиями
y x 3 ; y 0; x 1; x 2.
Решение:
y
1
0
2
x

85.

Задача
0
4 0
2
4 2
x
x
S (0 x )dx x dx
4 1 4 0
1
0
3
3
1
0 4 0 4,25кв.ед.
4

86.

Задача
Пример. Найти площадь фигуры,
ограниченной линиями
y x 2 2; y 6 x 2 .
Решение:
y
6
2 0 2
2
x

87.

Задача
Найдём точки пересечения линий, которые
в свою очередь будут пределами
интегрирования.
y x 2 2
2
2
2
x
2
6
x
2
x
8 x 2.
2
y 6 x
2
2
S [ 6 x 2 x 2 2 ] dx 8 2 x 2 dx
2
2
2
2x
16
16
32 64
16 16
8 x
32
кв.ед.
3 2
3
3
3
3
3

88.

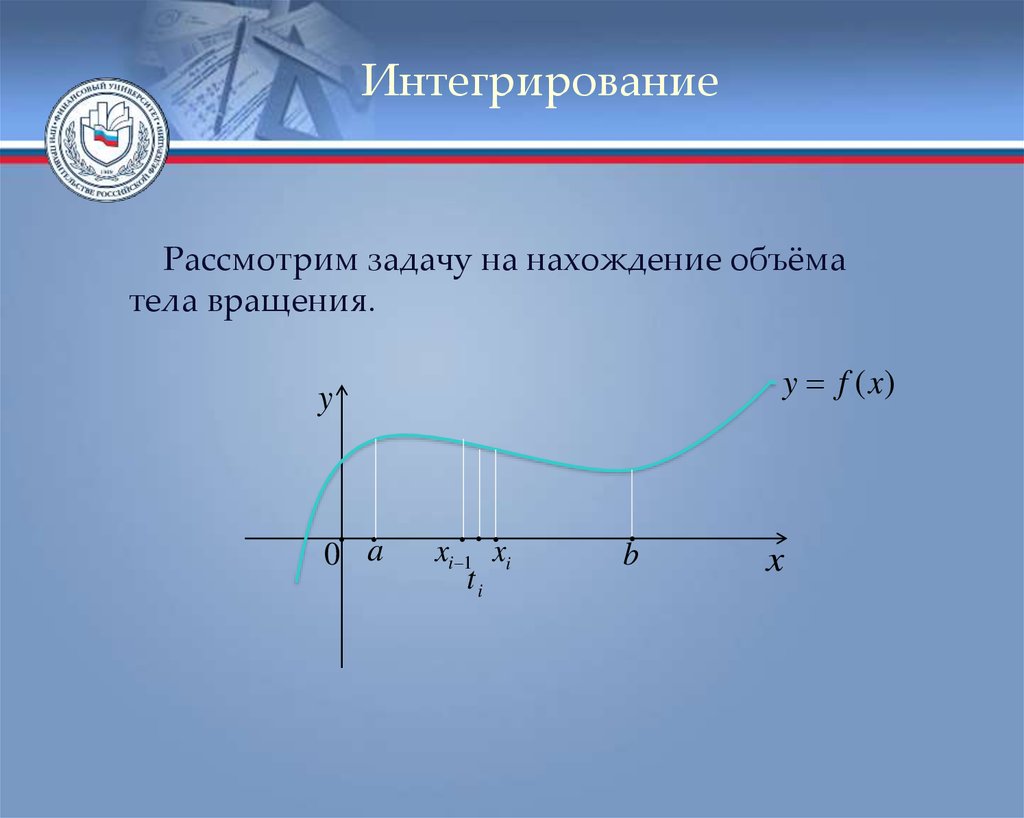
Интегрирование
Рассмотрим задачу на нахождение объёма
тела вращения.
y f (x)
y
0 a
xi 1 xi
ti
b
x

89.

Интегрирование
Vцил r 2 H
r f (ti ), H xi
b
V ( f ( x )) 2 dx
вокруг Ox
a
b
V ( f ( y )) 2 dy
a
вокруг Oy

90.

Задача
Пример. Вычислить объём тела вращения
вокруг оси абсцисс фигуры, ограниченной
линиями y=lnx, y=0, x=1, x=e.

91.

Задача
Решение.
y
y ln x
0
1
e
x

92.

Задача
e
u ln 2 x du
1
dv dx v x
V ln 2 x dx
2 ln x dx
e
e
2 ln x
2
( x ln x x
dx)
x
1
x
1
2dx
e
u 2 ln x du
e
(e 2 ln x dx)
x (e 2 x ln x 1 2dx)
1
1
dv dx v x
e
(e 2e 2 x 1 ) (e 2e 2e 2) (e 2) куб.ед .
e

93.

Задача
Пример. Вычислить объём тела вращения
вокруг оси ординат фигуры, ограниченной
2
2
линиями y x , y 0,5 x 2.

94.

Задача
Решение.
x2 2 y 4
y
4
2
0
x2 y
x

95.

Задача
Решение. Перевыразим x через y.
4
2 4
4
4
y
2
V ( ydy (2 y 4)dy ) (
( y 4 y) )
2
2
0
2
0
(8 4) 4
куб.ед .

96.

Интегрирование
Если функция непрерывна на [a; ) , то
называется
f
(
x
)
dx
интеграл вида
a
несобственным интегралом первого рода.
Аналогично
b
f ( x)dx, f ( x)dx.

97.

Интегрирование
В несобственных интегралах следует
осуществлять предельный переход:
b
f ( x)dx lim f ( x)dx
a
b
b
a
b
f ( x)dx lim f ( x)dx
a
a
Если предел конечен, то интеграл
называется сходящимся. Если бесконечен или
не существует, то он является расходящимся.

98.

Интегрирование
Рассмотрим:
0
0
f ( x)dx f ( x)dx f ( x)dx
Если хотя бы один из двух интегралов
расходится, то исходный тоже расходится.

99.

Интегрирование
Если подынтегральная функция имеет
разрывы на отрезке интегрирования, то её
интеграл является несобственным второго
рода.
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx , где с – точка
разрыва функции на отрезке [a; b]. Затем в
обоих интегралах осуществляем предельные
переходы.

100.

Интегрирование
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
t
lim
t c o
b
f ( x)dx lim f ( x)dx.
a
d c 0
d
Если хотя бы один из двух интегралов
расходится, то исходный тоже расходится.

101.

Интегрирование
Когда невозможно найти первообразную,
можно воспользоваться «признаком
сравнения». Пусть для всех значений х
выполняется неравенство 0 f ( x ) g ( x ),
тогда:
a ) Если сходится g ( x)dx, то сходится f ( x)dx,
a
a
a
a
b) Если расходится f ( x)dx, то расходится g ( x)dx.