Similar presentations:
Электростатика
1.
Электрический заряд. ЗаконКулона. Электростатическое поле.
Напряжённость поля. Линии
напряженности. Потенциал.
Эквипотенциальные поверхности.
Связь между напряженностью
электрического поля и
потенциалом. Энергия
взаимодействия системы зарядов.
Теорема Гаусса.
2.
• 4 фундаментальных взаимодействия:• сильное
• электромагнитное - определяется электрическим зарядом q
• слабое
• гравитационное
• Электрический заряд - это физическая скалярная величина,
характеризующая способность тел участвовать в
электромагнитных взаимодействиях.
• Свойства электрического заряда:
1. Два вида- положительные и отрицательный
2. В любой электрически изолированной системе алгебраическая
сумма зарядов не изменяется – закон сохранения
электрического заряда: q1+q2+…+qn=const .
3. Нигде и никогда в природе не возникает и не исчезает
электрический заряд одного знака. Появление положительного
электрического заряда всегда сопровождается появлением
равного по модулю отрицательного заряда.
3.
4. Электрический заряд является релятивистски инвариантным:его величина не зависит от системы отсчета.
5. Элементарный заряд e: любой заряд q равен
6. Элементарный заряд e является квантом (наименьшей порцией)
электрического заряда.
• В зависимости от концентрации свободных зарядов тела делятся
на проводники, диэлектрики и полупроводники.
• Проводники— это тела, в которых электрический заряд может
перемещаться по всему его объему (носители - электроны, ионы).
• Диэлектрики — тела, в которых практически отсутствуют
свободные заряды (идеальных изоляторов в природе не
существует)
• Полупроводники- занимают промежуточное положение между
проводниками и диэлектриками.
• Взаимодействие между зарядами осуществляется через поле.
Всякий электрический заряд q изменяет определенным образом
свойства окружающего его пространства – создает электрическое
поле.
4.
• Электрическое поле называется однородным, если во всех точкахвектор напряженности постоянен, как по величине, так и по
направлению
• Проявление поля- при помещении «пробного» заряда на него
действует сила.
• Сила, действующая на неподвижный пробный заряд q’, равна:
• где Е – напряженность электрического поля в данной точке.
• Точечный заряд – заряженное тело, размерами которого можно
пренебречь по сравнению с расстоянием эт этого тела до других
тел, несущих электрический заряд.
• Закон Кулона: сила взаимодействия двух точечных зарядов q1 и q2
пропорциональна величине каждого из зарядов и обратно
пропорционально квадрату расстояния r между ними:
• где k=4 0-коэффициент пропорциональности
5.
• Закон Кулона в векторном виде:• где r – вектор, проведенный от одного заряда к другому и
имеющий направление к заряду, на который действует сила f
• Напряженность поля- векторная величина равная:
• Из закона Кулона: напряженность поля неподвижного точечного
заряда q на расстоянии r от него:
• В Си [Е] = вольт / метр – в/м
• Принцип суперпозиции электрических полей: напряженность
поля системы зарядов равна векторной сумме напряженностей
полей, которые создавал бы каждый из зарядов системы в
отдельности:
• - позволяет вычислить напряженность поля любой системы
зарядов, представив в виде совокупности точечных зарядов.
6.
• Электрический диполь- система двух одинаковых по величинеразноименных точечных зарядов: +q и –q, расстояние между
которыми l значительно меньше, чем расстояние до точки
наблюдения
• Произведение
называется моментом диполя. Прямая
линия, соединяющая заряды называется осью диполя. Обычно
момент диполя считается направленным по оси диполя в
сторону положительного заряда.
• Электрическое поле наглядно изображается с помощью силовых
линий.
• Силовой линией электрического поля называется линия, в
каждой точке которой касательная совпадает с вектором
напряженности поля.
Число силовых линий, пронизывающих
воображаемую
площадку
1м2,
перпендикулярную полю, = величине
напряженности поля.
7.
• Силовые линии точечного заряда:• Силовые линии системы зарядов:
+q = -q
+q > -q
8.
• Т.к. густота линий = по величине E, то число линий N равно:• Количество линий, пронизывающих площадку dS,
перпендикулярную к вектору E, равно EdS.
• Пусть площадка dS ориентирована так, что нормаль образует с
вектором E угол , тогда число линий через площадку:
• где En- составляющая вектора Е по направлению нормали к
площадке.
• Поток вектора E есть величина:
• Полное число силовых линий, проходящих через поверхность S
называется потоком вектора напряженности через эту
поверхность.
• Поток вектора есть скаляр: в зависимости от величины угла α
может быть положительным и отрицательным
9.
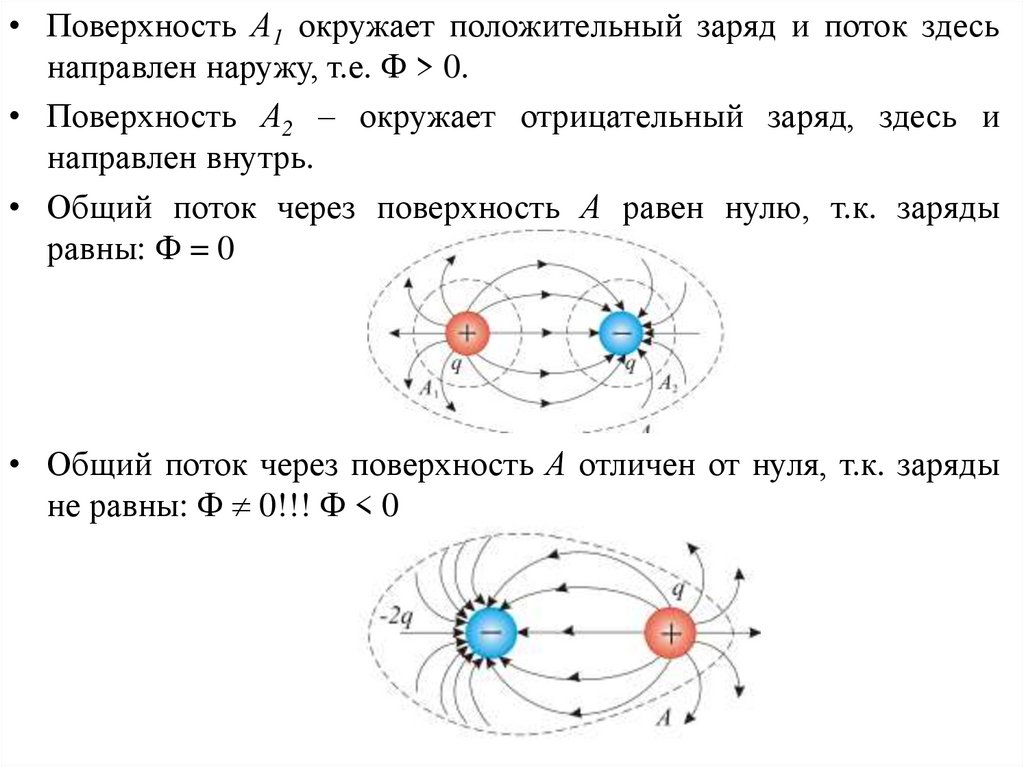
• Поверхность А1 окружает положительный заряд и поток здесьнаправлен наружу, т.е. > 0.
• Поверхность А2 – окружает отрицательный заряд, здесь и
направлен внутрь.
• Общий поток через поверхность А равен нулю, т.к. заряды
равны: = 0
• Общий поток через поверхность А отличен от нуля, т.к. заряды
не равны: 0!!! < 0
10.
• По принципу суперпозиции:• Подставим в поток:
• где Eni – нормальная составляющая напряженности поля,
создаваемого i-м зарядом в отдельности.
• Т.к.
, то получим:
• Теорема Гаусса в интегральной форме: поток вектора
напряженности электрического поля через замкнутую
поверхность равен алгебраической сумме заключенных внутри
этой поверхности зарядов, деленной на 0.
• Если заряд распределен внутри поверхности непрерывно с
объемной плотностью :
11.
• Интегральнаяформа
теоремы
Гаусса
характеризует
соотношения между источниками электрического поля
(зарядами)
и
характеристиками
электрического
поля
(напряженностью или индукцией) в объеме V произвольной, но
достаточной для формирования интегральных соотношений,
величины.
12.
• Рассмотрим поле точечного неподвижного заряда.• Работа dА, которая совершается силами поля неподвижного
точечного заряда q над перемещающимся в этом поле точечным
зарядом q’, на элементарном пути dl:
• Работа на пути 1-2:
• Работа не зависит от пути перемещения, зависит от начального
и конечного положений этого заряда.
• Силы, действующие на заряд q’ в поле неподвижного заряда q,
являются потенциальными.
• Для системы зарядов:
13.
• Учитывая:• Работа потенциальных сил на замкнутом пути равна нулю
• Работа сил поля наад зарядом q’ при обходе по замкнутому
контуру:
• Теорем о циркуляции вектора Е электростатического поля:
• Поле обладающим таким свойством называют потенциальным.
• Электростатическое поле – потенциальное поле
14.
• Работа может быть представлена как разность потенциальнойэнергии заряда q’ в точках 1 и 2 поля заряда q:
• Потенциал поля в данной точке есть скалярная величина,
численно равная потенциальной энергии, которой обладает в
данной точке поля единичный положительный заряд:
• Потенциал точечного заряда:
• Потенциал поля, создаваемого системой зарядов, равен
алгебраической сумме потенциалов, создаваемых каждым из
зарядов в отдельности:
• Си [ ] = вольт
15.
Электрическое поле описывается векторной функцией E(r).
Найдем связь и Е.
Пусть перемещение dl паралельно оси X.
Тогда dl=idx, где i – орт оси X, dx- приращение координаты х.
Тогда:
• Т.к.
, то
• Для Ey и Ez - аналогично, тогда:
• Напряжённость в какой-либо точке электрического поля равна
градиенту потенциала в этой точке, взятому с обратным
знаком:
16.
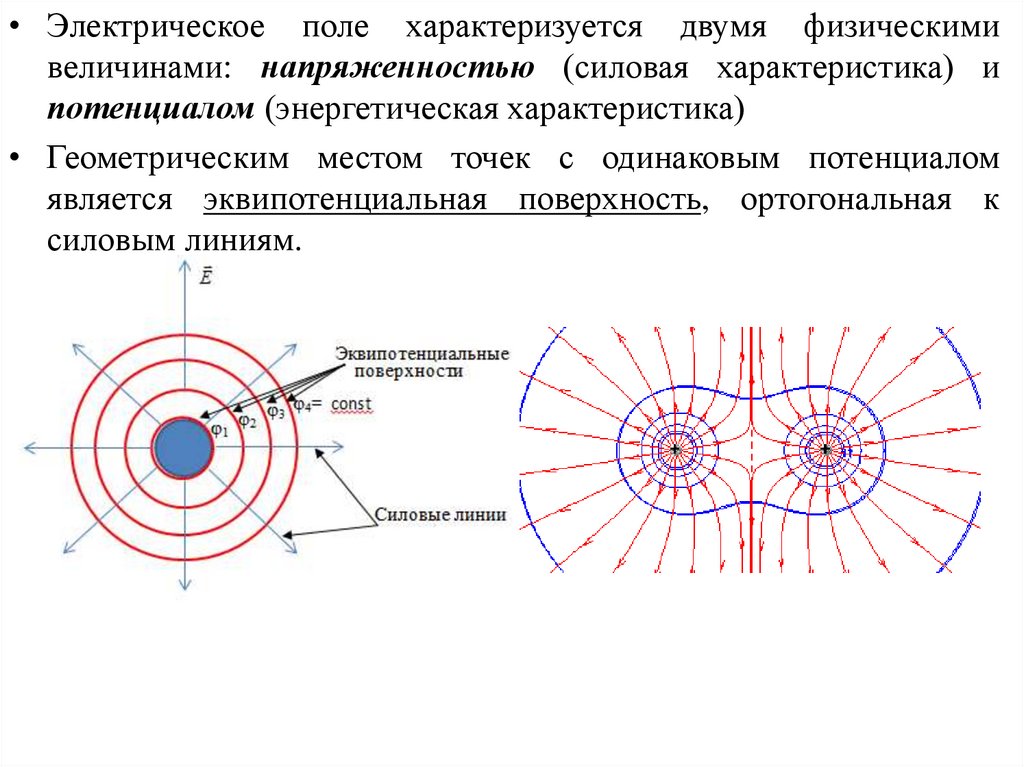
• Электрическое поле характеризуется двумя физическимивеличинами: напряженностью (силовая характеристика) и
потенциалом (энергетическая характеристика)
• Геометрическим местом точек с одинаковым потенциалом
является эквипотенциальная поверхность, ортогональная к
силовым линиям.














 physics
physics








