Основные теоремы электростатики. Тема 2

1. Омский государственный технический университет Кафедра физики

Калистратова Л.Ф.
Электронные лекции по разделам
электромагнетизма
(электростатика, постоянный ток, магнетизм)
17 лекций
(34 аудиторных часа)

2. Тема 2. Основные теоремы электростатики

План лекции
1. Циркуляция вектора напряжённости. Теорема о
циркуляции вектора напряжённости.
2. Поток вектора напряжённости. Теорема Гаусса.
3. Методы расчёта электрических полей.
4. Электростатическое поле точечного заряда.
5. Электростатическое поле диполя.

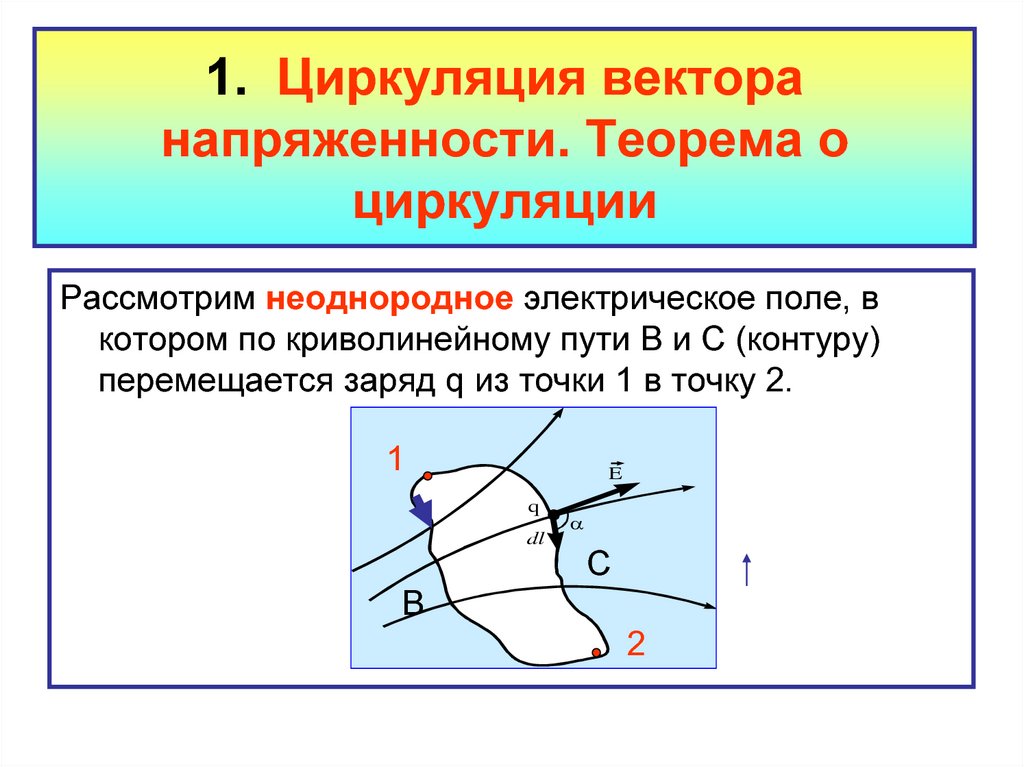
3. 1. Циркуляция вектора напряженности. Теорема о циркуляции

Рассмотрим неоднородное электрическое поле, в
котором по криволинейному пути В и С (контуру)
перемещается заряд q из точки 1 в точку 2.
1
E
q
dl
С
В
2

4.

В предыдущей теме показано, что работа сил
электростатического поля:
- не зависит от формы пути:
А1В2 = А1С2;
- равна нулю при перемещении заряда по некоторому
замкнутому контуру.
A dA 0
L
Эти условия можно сформулировать несколько иначе,
введя понятие о циркуляции вектора
напряженности.

5.

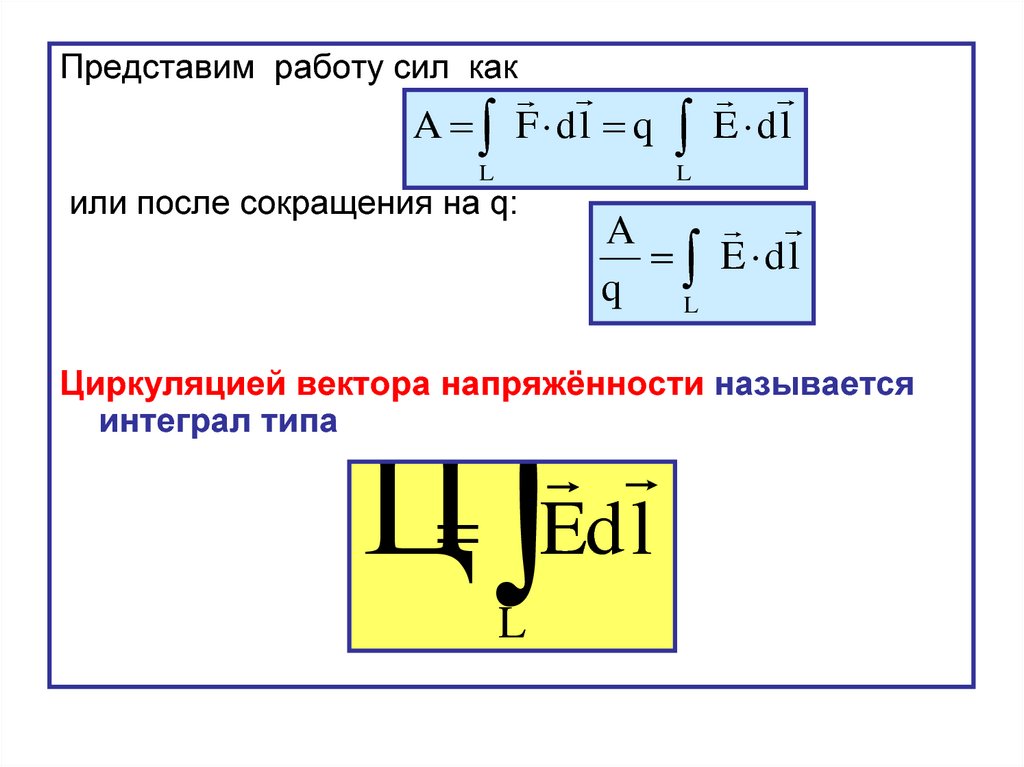
Представим работу сил как
A
F dl q
L
или после сокращения на q:
E dl
L
A
E dl
q
L
Циркуляцией вектора напряжённости называется
интеграл типа
Ц Ed l
L

6.

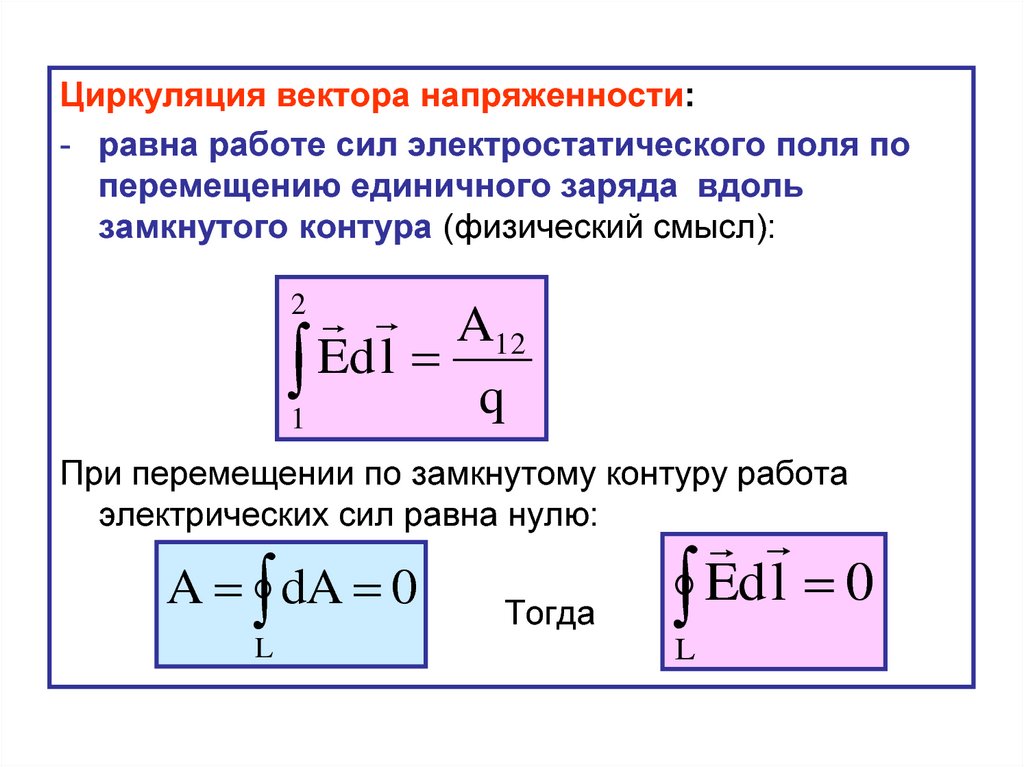
Циркуляция вектора напряженности:
- равна работе сил электростатического поля по
перемещению единичного заряда вдоль
замкнутого контура (физический смысл):
A12
1 Ed l q
2
При перемещении по замкнутому контуру работа
электрических сил равна нулю:
A dA 0
L
Тогда
Ed l 0
L

7.

E
d
l
0
L
Теорема о циркуляции вектора напряжённости:
циркуляция вектора напряжённости
электростатического поля по замкнутому контуру
равна нулю.
Физический смысл теоремы о циркуляции:
электростатическое поле – потенциально;
электрические силы – консервативны.

8. 2. Поток вектора напряжённости. Теорема Гаусса

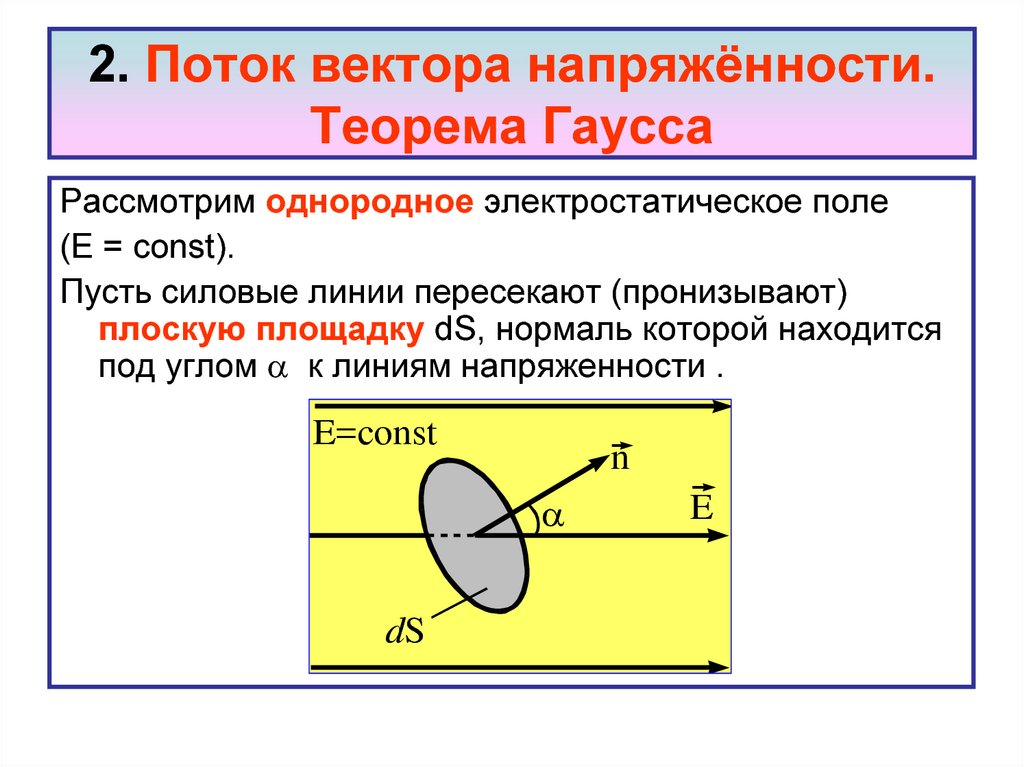
Рассмотрим однородное электростатическое поле
(Е = const).
Пусть силовые линии пересекают (пронизывают)
плоскую площадку dS, нормаль которой находится
под углом к линиям напряженности .
E=const
n
dS
E

9.

Элементарный поток вектора напряжённости
определяется выражением:
dN EdS EdS cos E n dS
En – проекция вектора E на нормаль
n к площадке dS.
Элементарный поток вектора напряжённости:
– скалярная величина;
- равен общему числу линий, пронизывающих
площадку dS;
- является положительной величиной, если угол –
острый, и отрицательной, если угол - тупой;
B 2
- измеряется в вольтах на метр:
N 1
ì
ì
 ì

10.

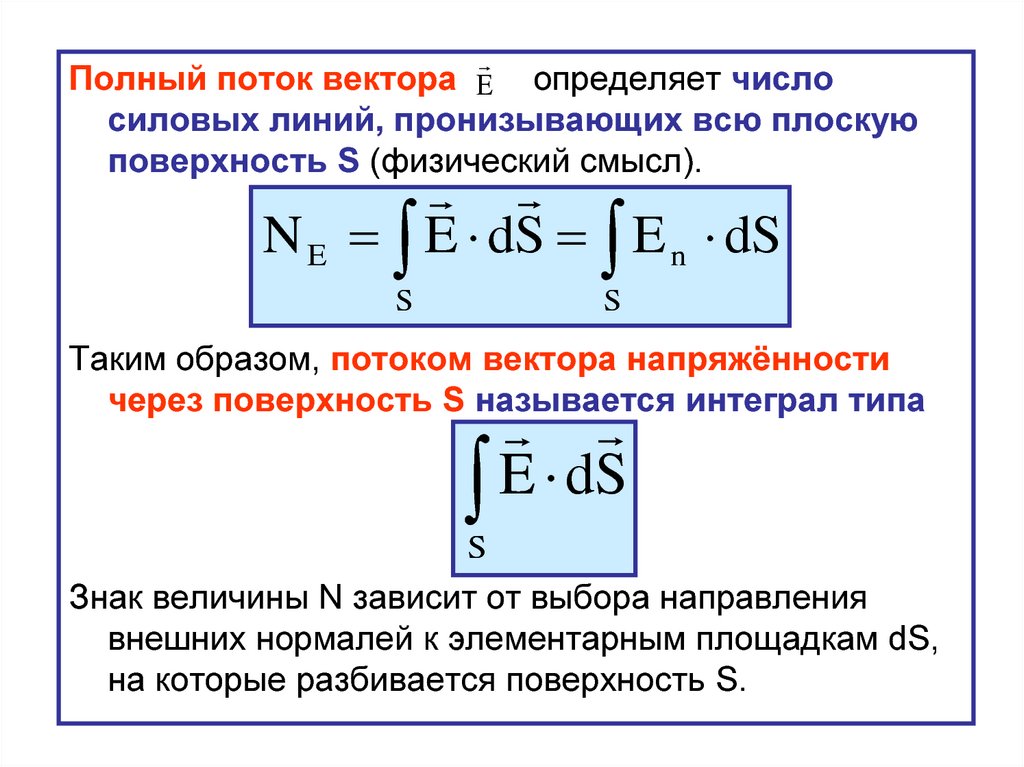
Полный поток вектора E
определяет число
силовых линий, пронизывающих всю плоскую
поверхность S (физический смысл).
N E E dS E n dS
S
S
Таким образом, потоком вектора напряжённости
через поверхность S называется интеграл типа
E
d
S
S
Знак величины N зависит от выбора направления
внешних нормалей к элементарным площадкам dS,
на которые разбивается поверхность S.

11.

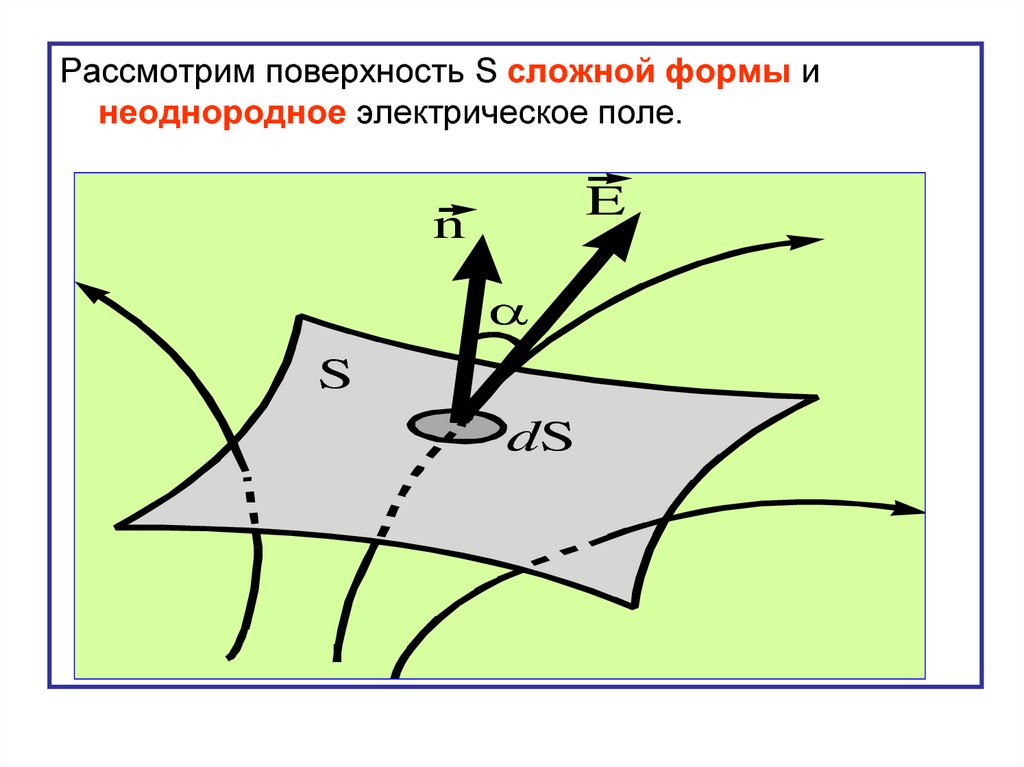
Рассмотрим поверхность S сложной формы и
неоднородное электрическое поле.
E
n
S
dS

12.

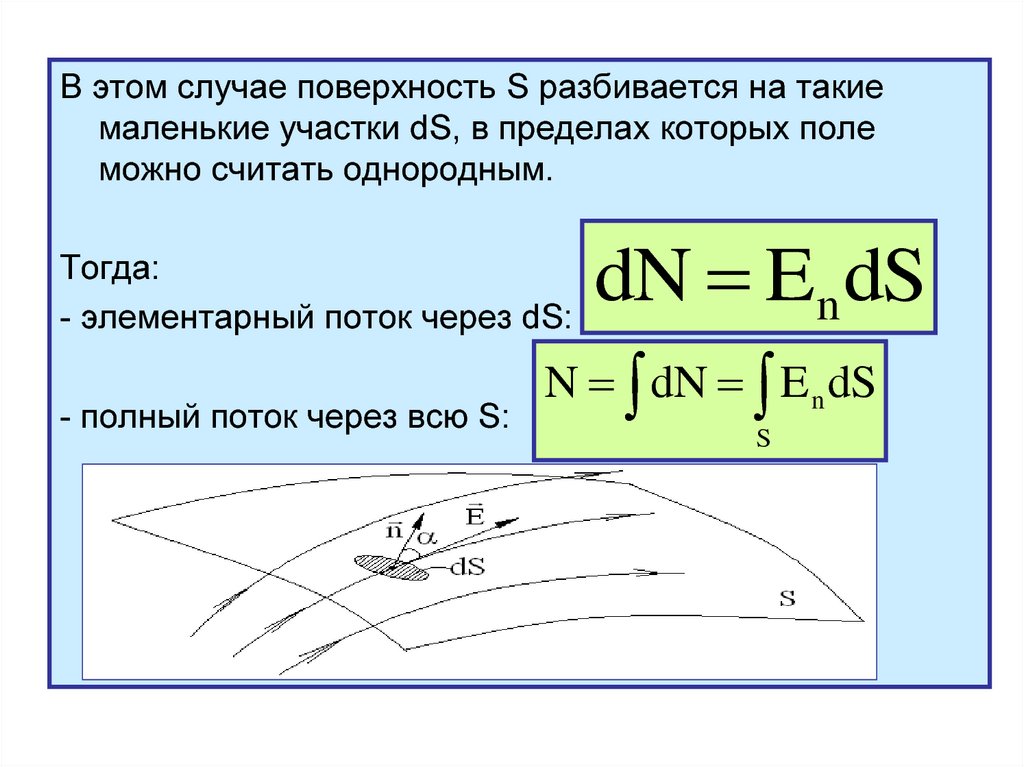
В этом случае поверхность S разбивается на такие
маленькие участки dS, в пределах которых поле
можно считать однородным.
Тогда:
- элементарный поток через dS:
- полный поток через всю S:
dN En dS
N dN E n dS
S

13.

Если поверхность S будет замкнутой, то силовые
линии неоднородного поля будут входить в
поверхность и выходить из неё.
В этом случае поверхность S также разбивается на
маленькие участки dS.
Элементарный поток через площадку dS будет
положительным, если угол α - острый (линии
напряженности выходят из объёма, ограниченного
поверхностью).
Если же угол α – тупой , то поток через площадку dS
отрицателен (линии напряжённости входят в
объём, ограниченный поверхностью S).

14.

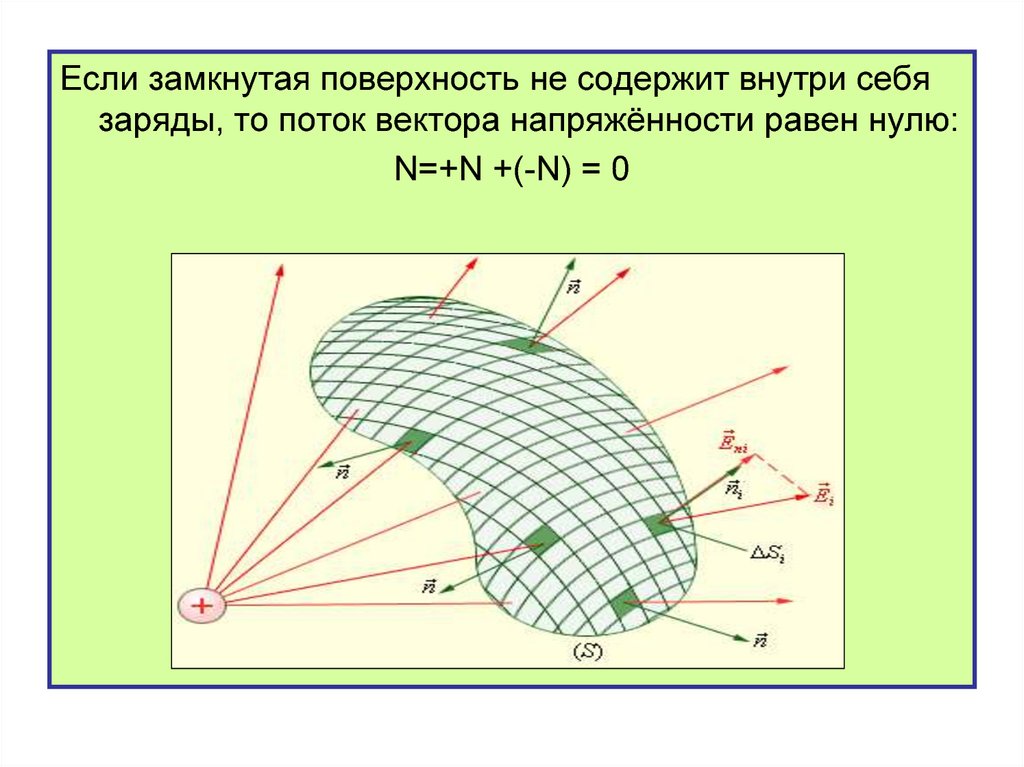
Если замкнутая поверхность не содержит внутри себя
заряды, то поток вектора напряжённости равен нулю:
N=+N +(-N) = 0

15.

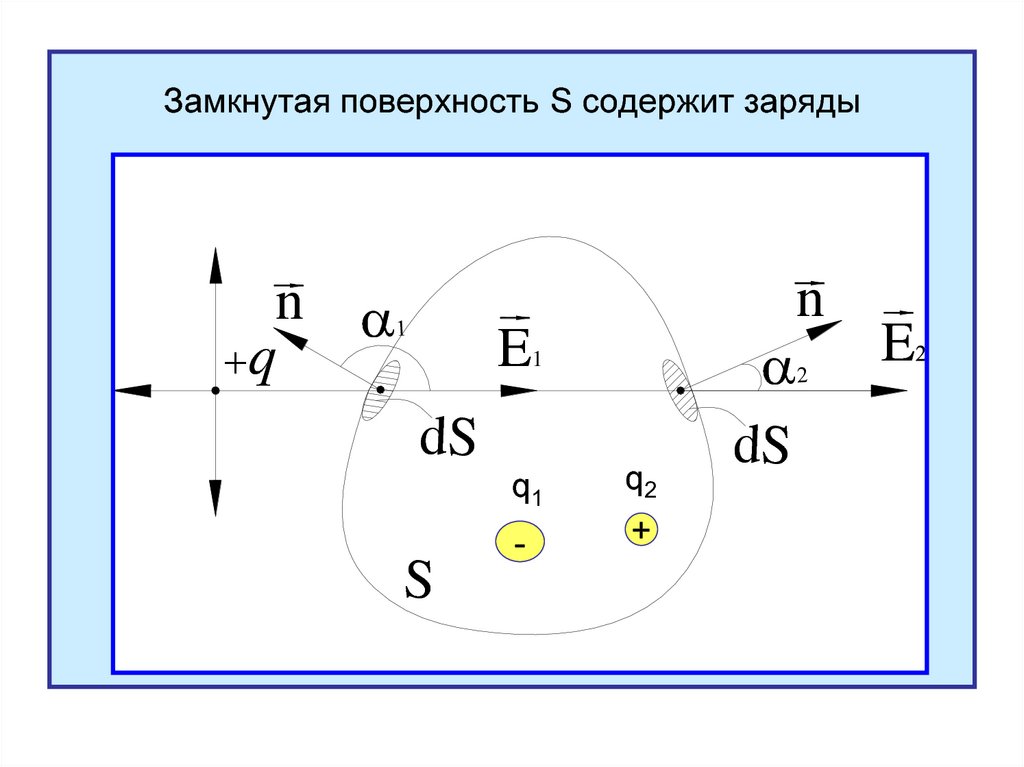
Замкнутая поверхность S содержит заряды
n
q
E1
dS
S
q1
q2
-
+
n
dS
E

16.

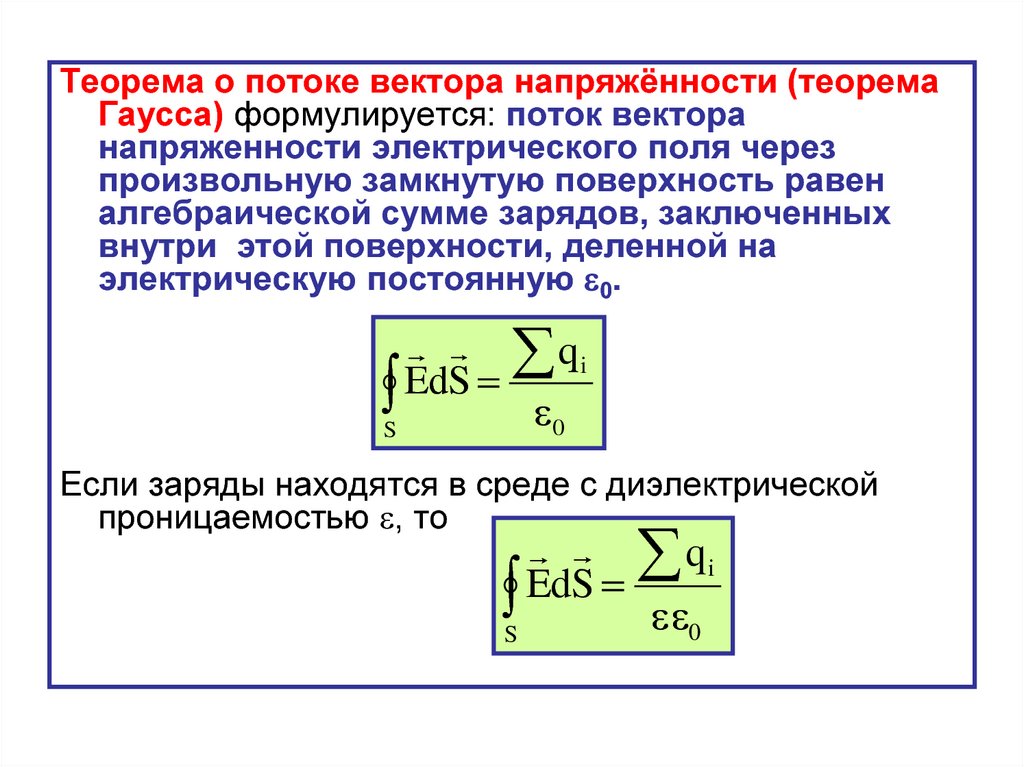
Теорема о потоке вектора напряжённости (теорема
Гаусса) формулируется: поток вектора
напряженности электрического поля через
произвольную замкнутую поверхность равен
алгебраической сумме зарядов, заключенных
внутри этой поверхности, деленной на
электрическую постоянную 0.
qi
S EdS 0
Если заряды находятся в среде с диэлектрической
проницаемостью , то
qi
S EdS 0

17.

Физическое содержание теоремы Гаусса:
- силовые линии электростатического поля
начинаются и оканчиваются на неподвижных
зарядах;
- источником электростатического поля являются
неподвижные заряды.

18. 3. Методы расчёта электрических полей

Важной прикладной задачей электростатики является
расчет электрических полей, имеющихся в
различных приборах и аппаратах – конденсаторах,
электронных лампах, кабелях и т.д.
Рассчитать поле – значит определить в любой его
точке модуль и направление вектора напряженности
и величину потенциала.
Эта задача, в общем случае, решается на основе
принципа суперпозиции с:
- применением закона Кулона;
- применением теоремы Гаусса.

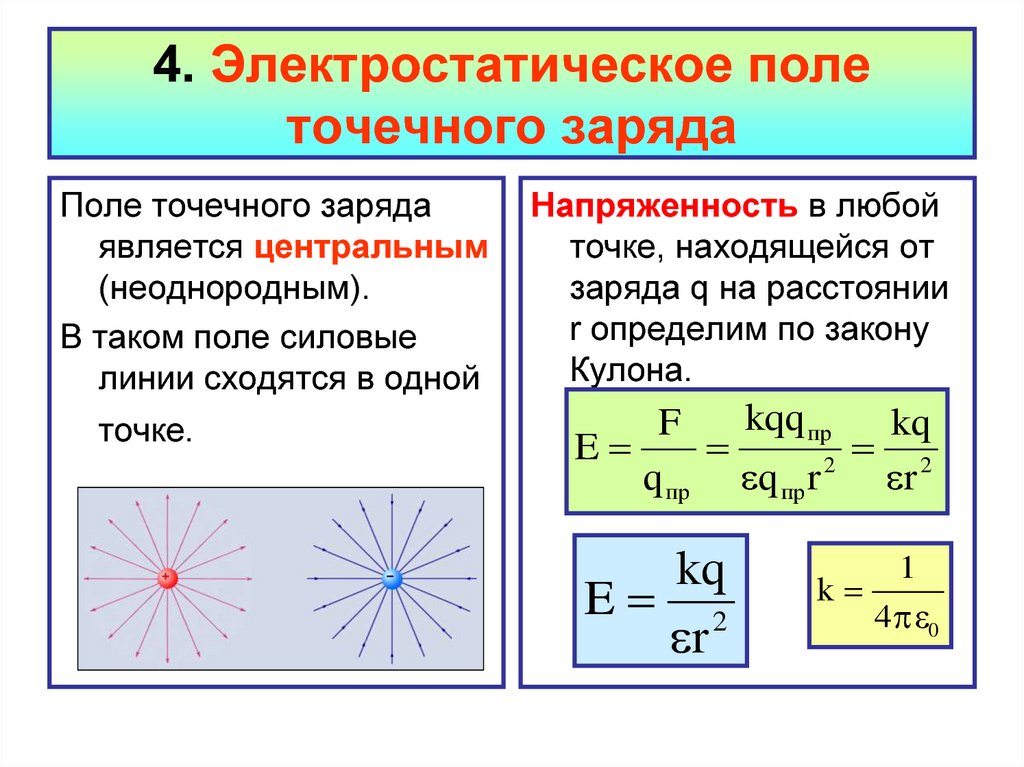
19. 4. Электростатическое поле точечного заряда

Поле точечного заряда
является центральным
(неоднородным).
В таком поле силовые
линии сходятся в одной
точке.
Напряженность в любой
точке, находящейся от
заряда q на расстоянии
r определим по закону
Кулона.
kqq пр
F
kq
E
2
2
q пр q пр r
r
kq
E 2
r
1
k
4 0

20.

Разность потенциалов двух точек поля с
потенциалами 1 и 2 определим на основе
формулы
d E dr
2
Проинтегрируем это выражение:
Отсюда
r2
kq
d r r 2 dr
1
1
kq 1 1
2 1
r2 r1
r1 и r2 – расстояния от заряда q до точек, потенциалы
которых равны 1 и 2 соответственно.
Потенциал точечного заряда:
kq
r

21.

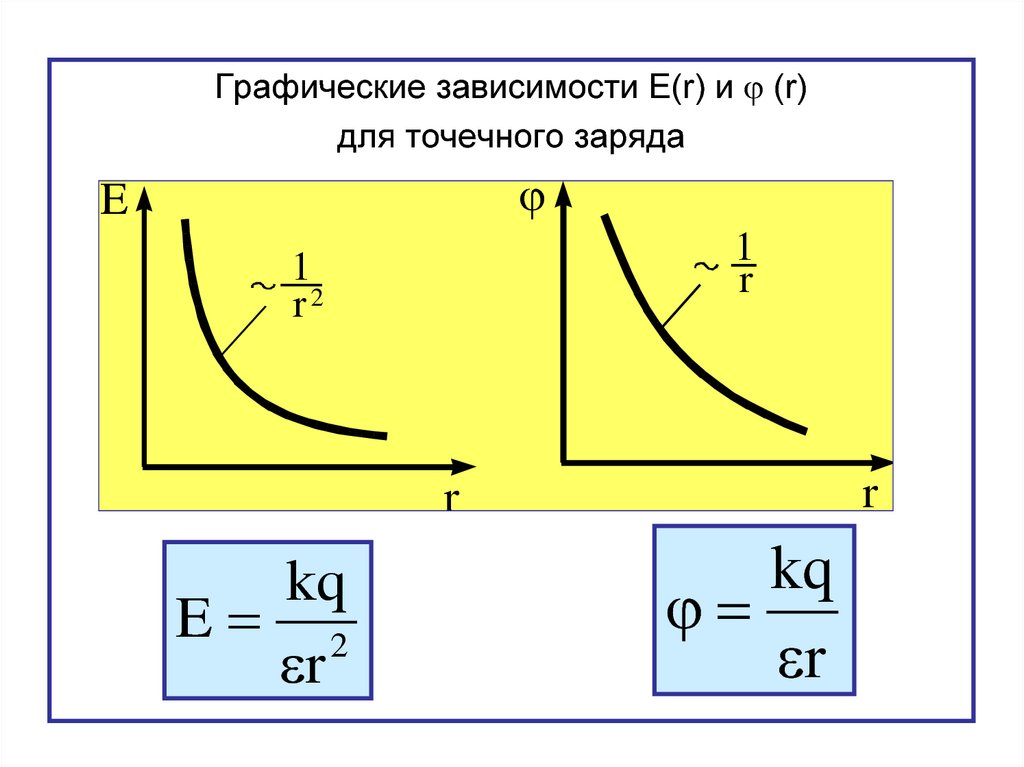
Графические зависимости E(r) и (r)
для точечного заряда
E
1
r
1
r2
r
r
kq
E 2
r
kq
r

22.

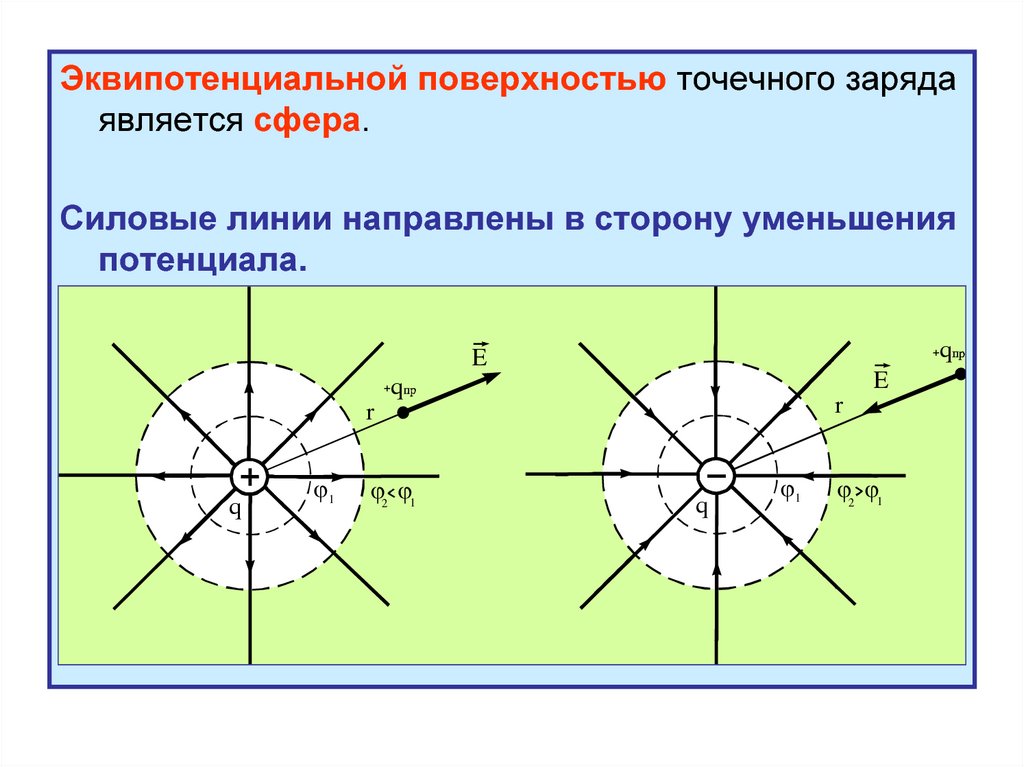
Эквипотенциальной поверхностью точечного заряда
является сфера.
Силовые линии направлены в сторону уменьшения
потенциала.
+
E
+
E
q
r
r
q
1
1
2
q
1
1
2
q

23. 5. Электростатическое поле диполя

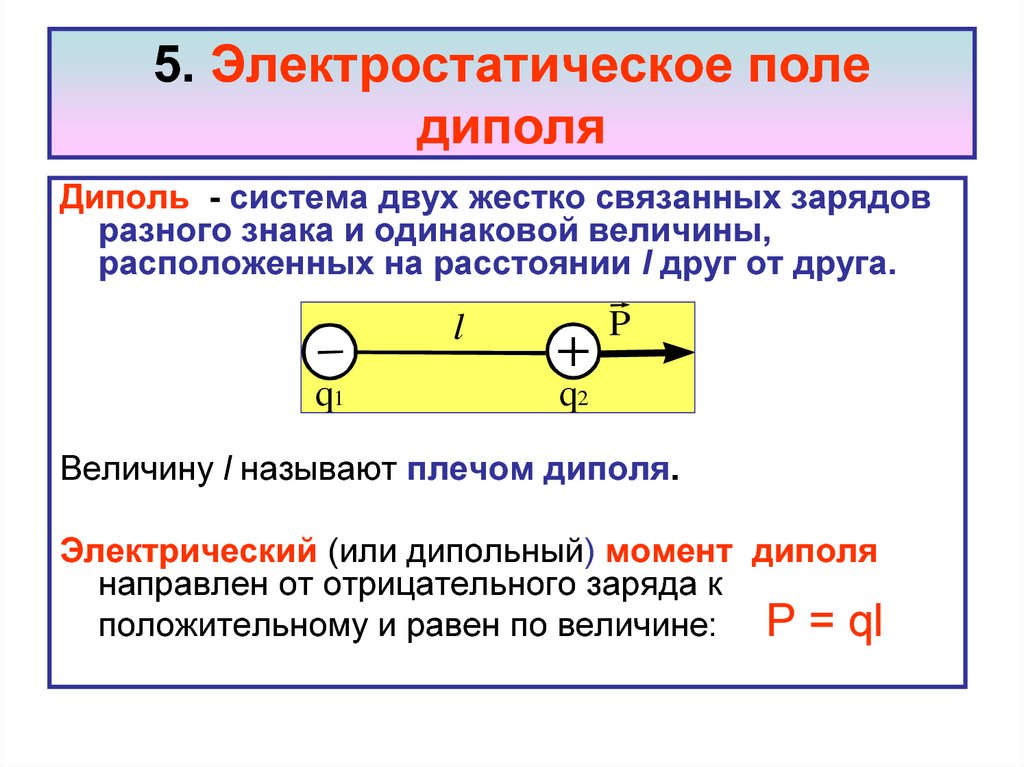
Диполь - система двух жестко связанных зарядов
разного знака и одинаковой величины,
расположенных на расстоянии l друг от друга.
l
q1
+
P
q2
Величину l называют плечом диполя.
Электрический (или дипольный) момент диполя
направлен от отрицательного заряда к
положительному и равен по величине: P = ql

24.

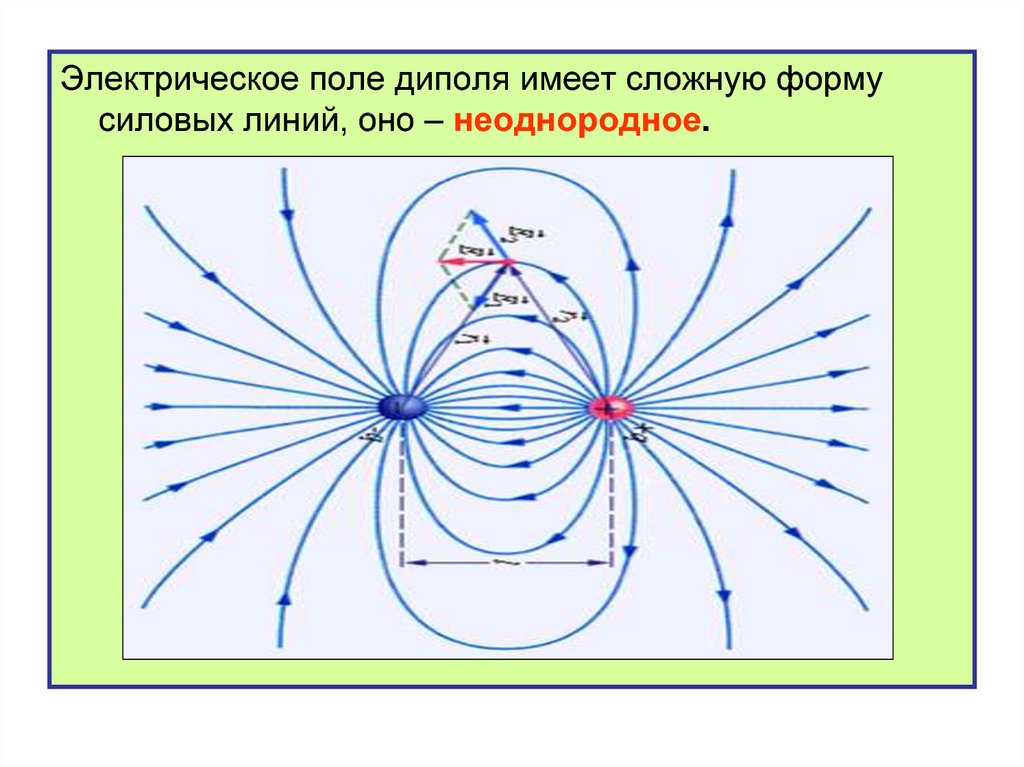
Электрическое поле диполя имеет сложную форму
силовых линий, оно – неоднородное.

25.

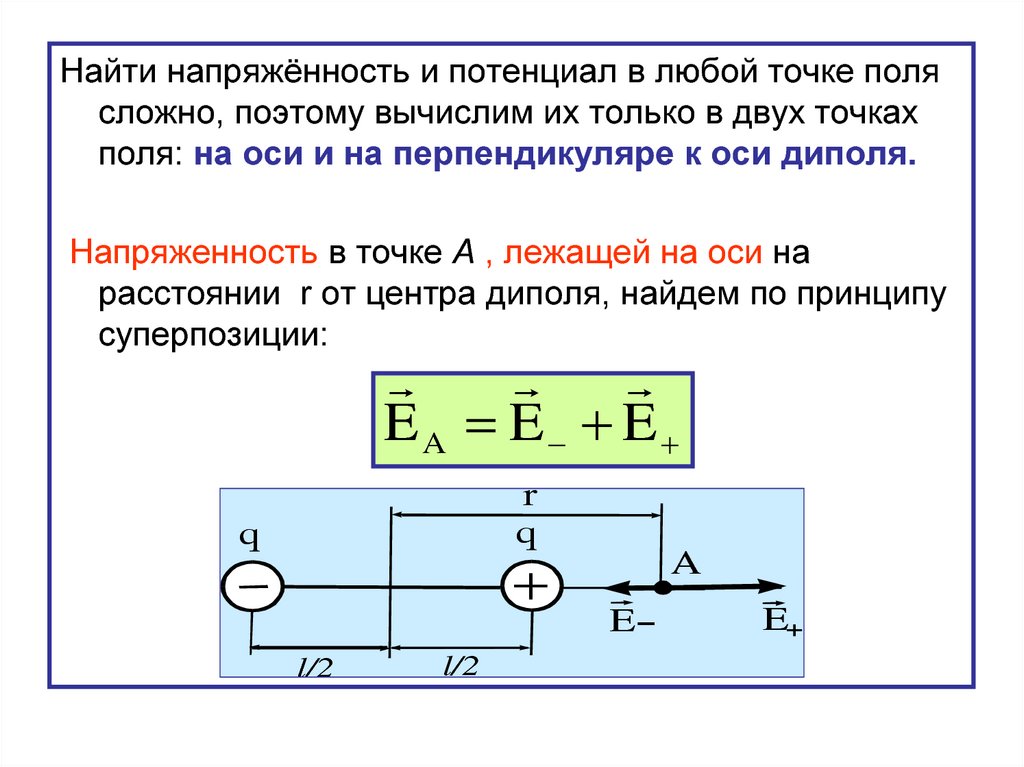
Найти напряжённость и потенциал в любой точке поля
сложно, поэтому вычислим их только в двух точках
поля: на оси и на перпендикуляре к оси диполя.
Напряженность в точке А , лежащей на оси на
расстоянии r от центра диполя, найдем по принципу
суперпозиции:
EA E E
r
q
q
+
l/2
l/2
A
E
_
E+

26.

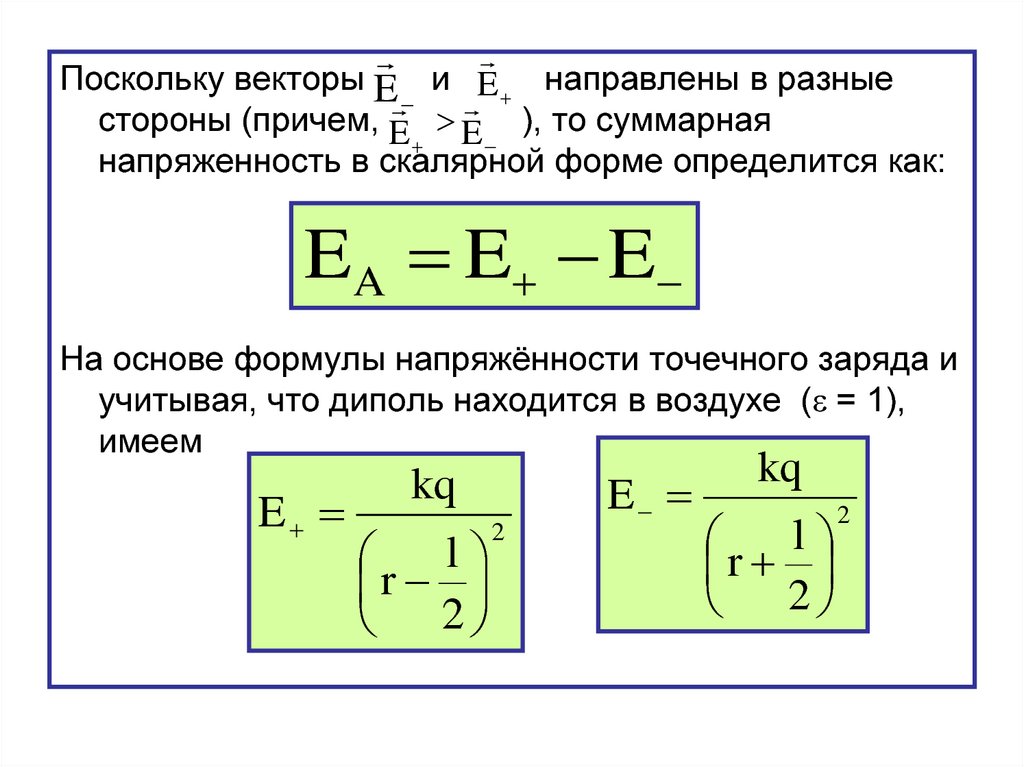
Поскольку векторы E и E направлены в разные
стороны (причем, E E ), то суммарная
напряженность в скалярной форме определится как:
EA E E
На основе формулы напряжённости точечного заряда и
учитывая, что диполь находится в воздухе ( = 1),
имеем
E
kq
l
r
2
2
E
kq
l
r
2
2

27.

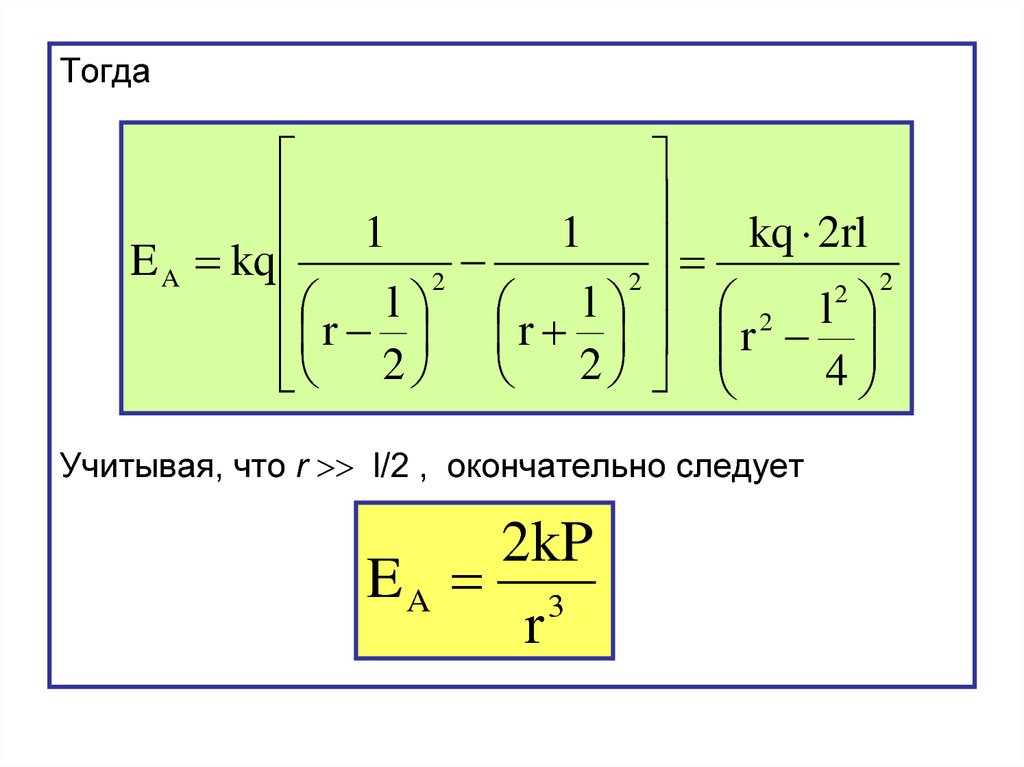
Тогда
1
1
kq 2rl
E A kq
2
2
2 2
l
l
2 l
r r r
4
2 2
Учитывая, что r l/2 , окончательно следует
2kP
EA 3
r

28.

Проделаем те же операции для точки В, лежащей на
перпендикуляре к оси диполя на расстоянии r от нее
и на одинаковом расстоянии от зарядов.
У
E+
E
B
Х
E_
r
l/2
l/2

29.

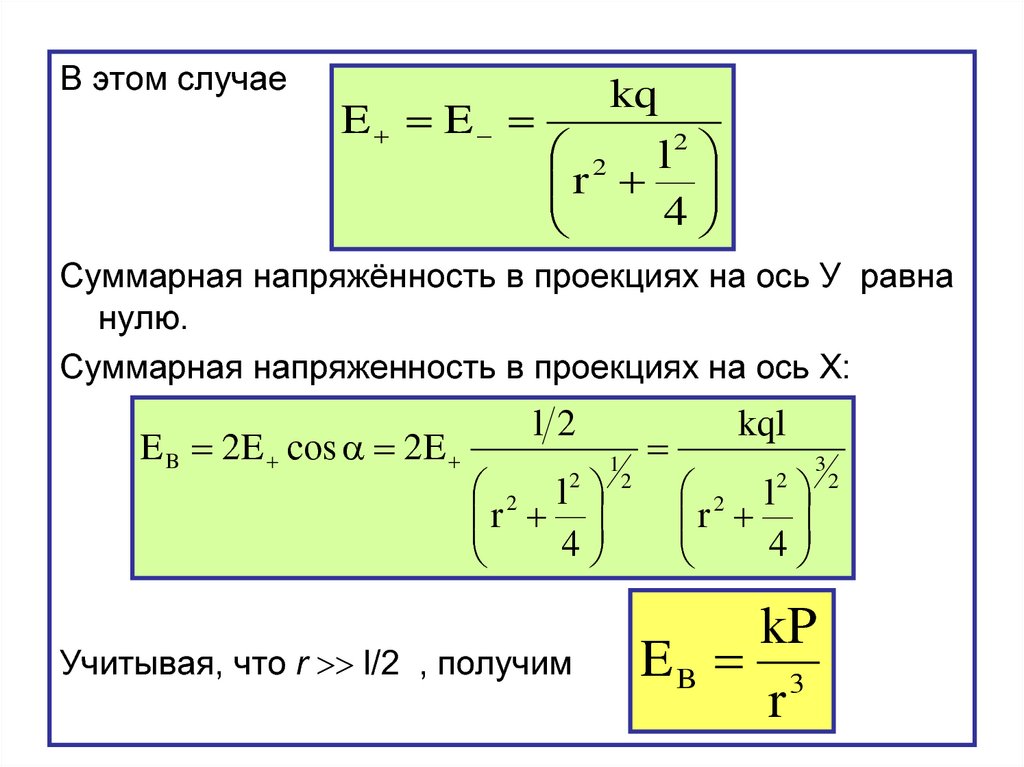
В этом случае
kq
E E
2 l2
r
4
Суммарная напряжённость в проекциях на ось У равна
нулю.
Суммарная напряженность в проекциях на ось Х:
E B 2E cos 2E
l2
2 l
r
4
2
Учитывая, что r l/2 , получим
1
2
kql
2 l
r
4
2
3
kP
EB 3
r
2

30.

Напряжённость диполя
на перпендикуляре к оси
на оси
2kP
E 3
r
kP
E 3
r
в произвольной точке
kP
2
E 3 1 3 cos
r
Потенциал
в произвольной точке определится как:
kP cos
2
r

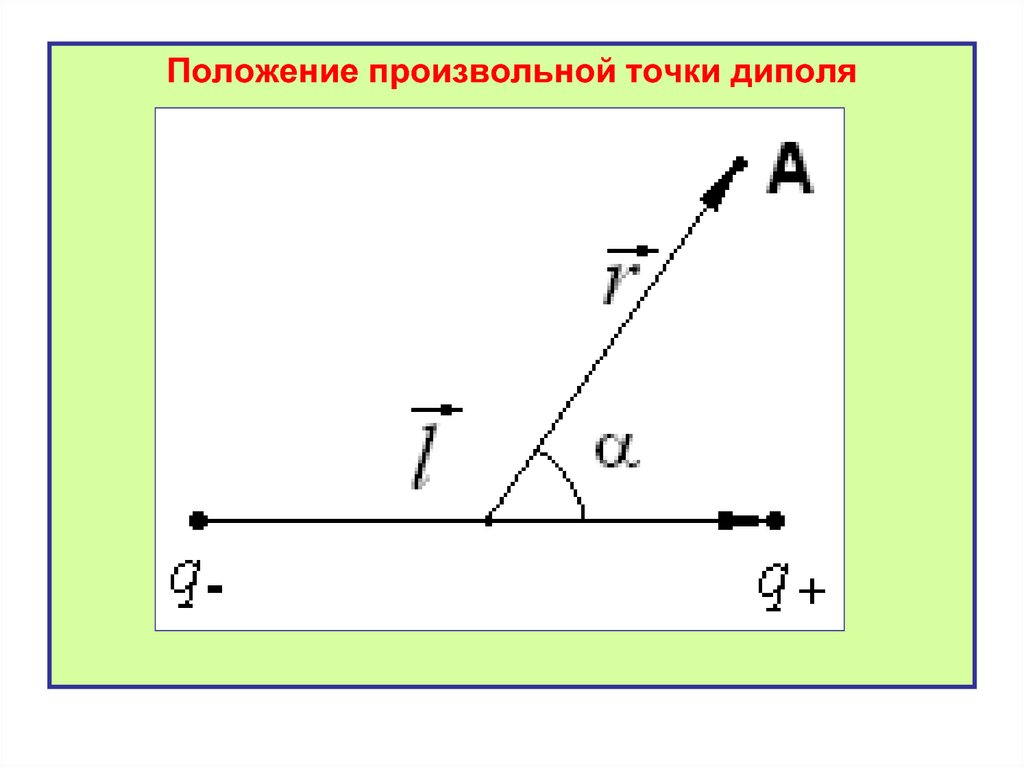
31.

Положение произвольной точки диполя

32.

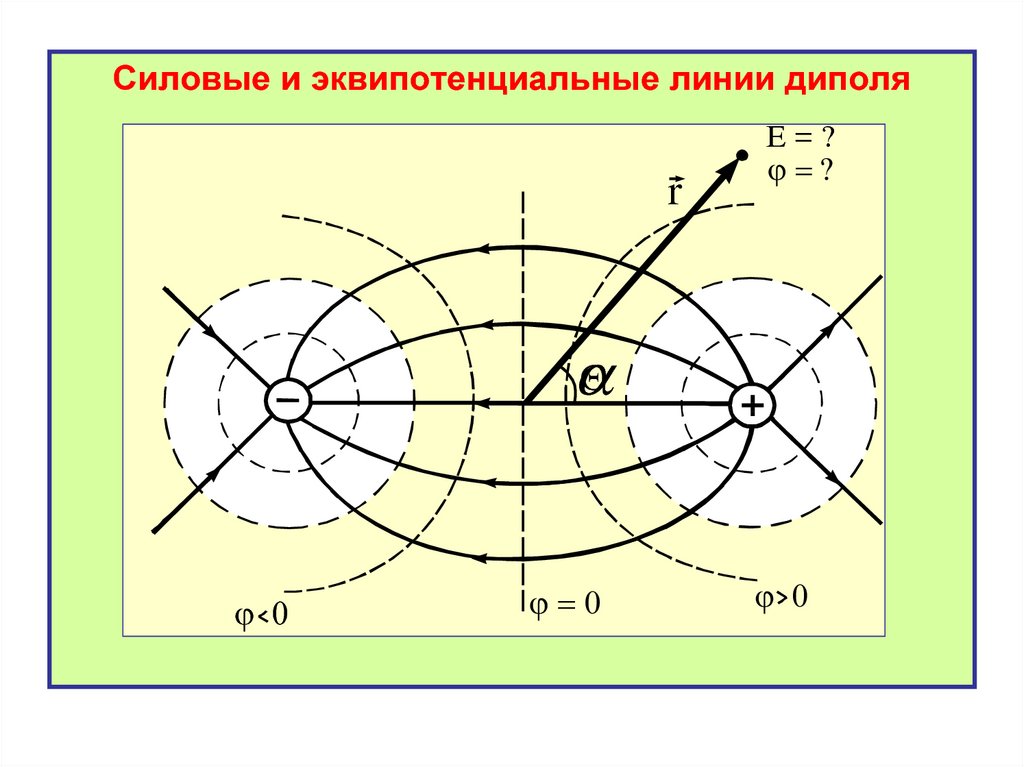
Силовые и эквипотенциальные линии диполя
r
E=?