Similar presentations:
Электростатика. Основные теоремы (в вакууме)
1. ЭЛЕКТРОСТАТИКА основные теоремы (в вакууме)
2.
1. Теорема о циркуляции2. Поток вектора напряженности электростатического поля
3. Теорема Гаусса
4. Поле заряженной сферы (металлический шар)
Поле равномерно заряженного шара (шар из
диэлектрика)
5. Поле заряженной плоскости (двух плоскостей)
6. Поле полого цилиндра, заряженной нити
7. Теорема Остроградского-Гаусса
8. Дивергенция напряженности электростатического поля
.
9. Теорема Гаусса в дифференциальной форме
10. Уравнение Пуассона
11. Ротор векторного поля
12. Теорема Стокса
13. Основные теоремы ЭП в вакууме
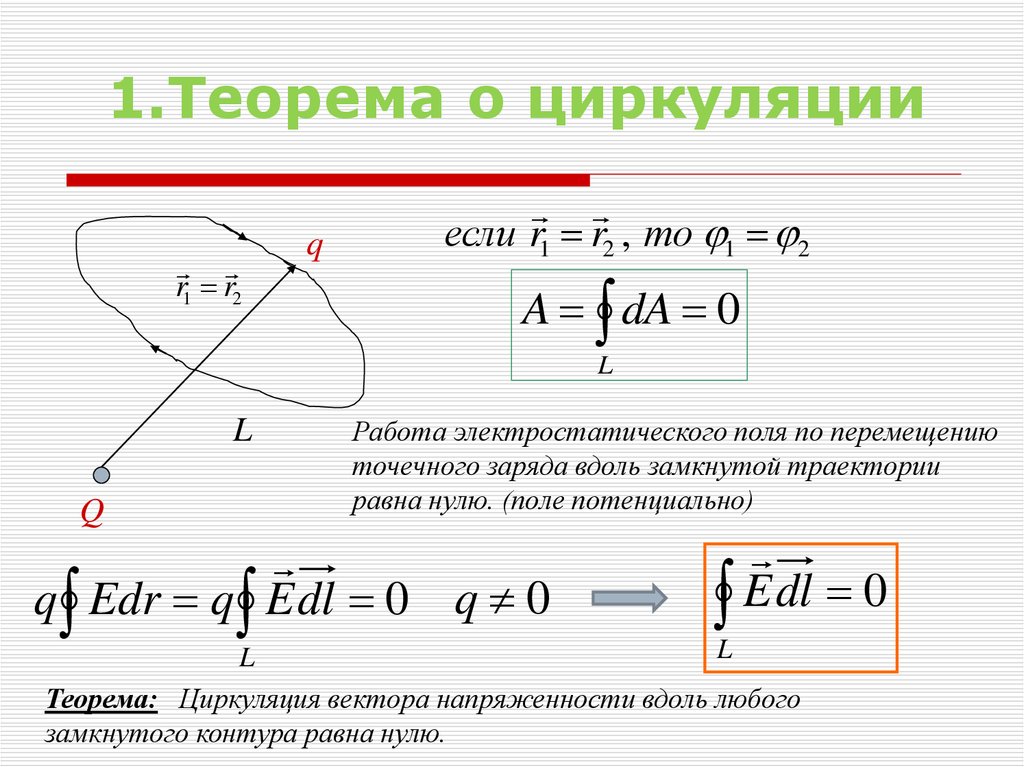
3. 1.Теорема о циркуляции
r1 r2q
если r1 r2 , то 1 2
A dA 0
L
L
Q
Работа электростатического поля по перемещению
точечного заряда вдоль замкнутой траектории
равна нулю. (поле потенциально)
q Edr q E dl 0 q 0
E dl 0
L
L
Теорема: Циркуляция вектора напряженности вдоль любого
замкнутого контура равна нулю.
4.
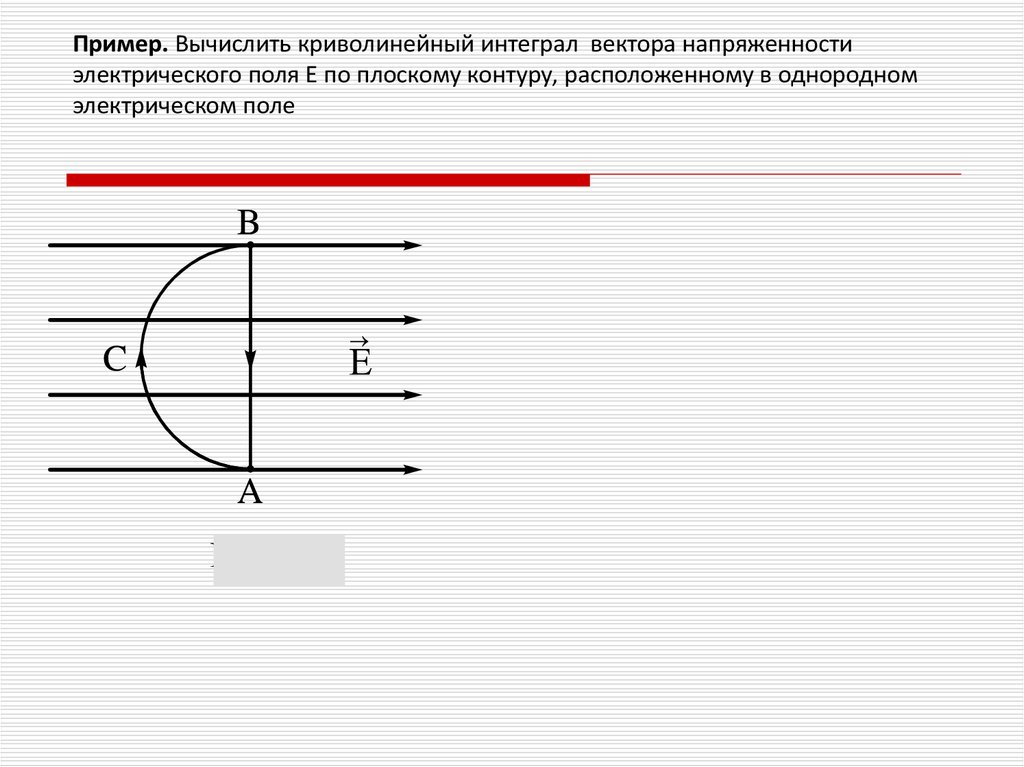
Пример. Вычислить криволинейный интеграл вектора напряженностиэлектрического поля Е по плоскому контуру АВС, расположенному в
однородном электрическом поле
5.
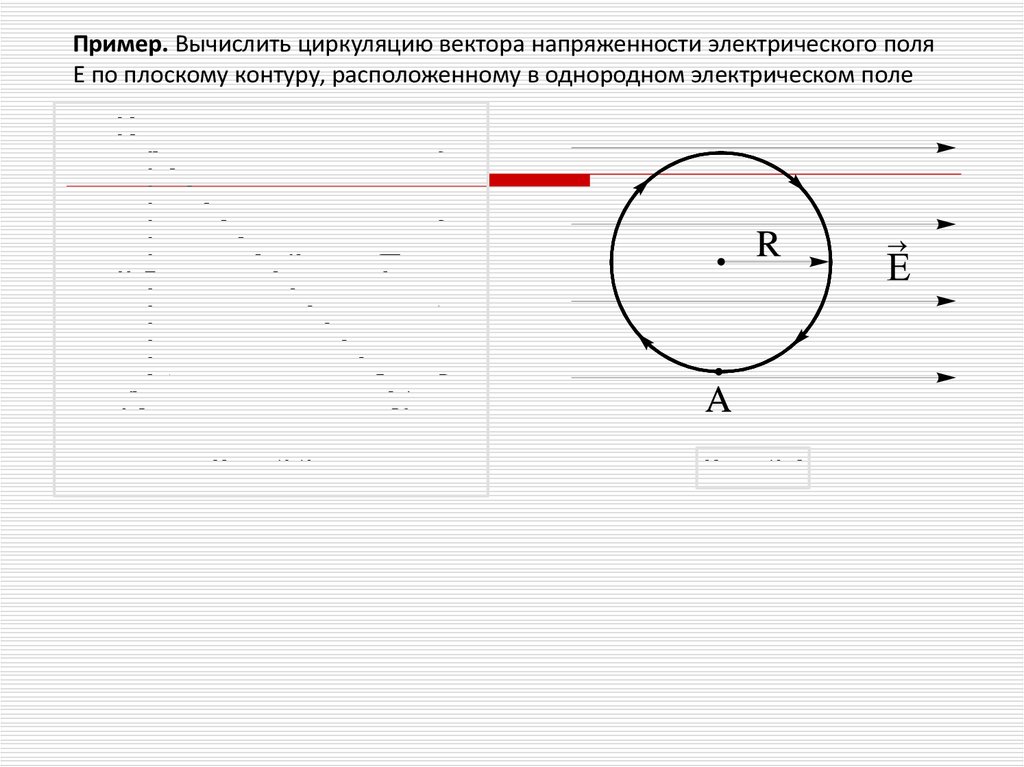
Пример. Вычислить циркуляцию вектора напряженности электрического поляЕ по плоскому контуру, расположенному в однородном электрическом поле
6.
Пример. Вычислить криволинейный интеграл вектора напряженностиэлектрического поля Е по плоскому контуру, расположенному в однородном
электрическом поле
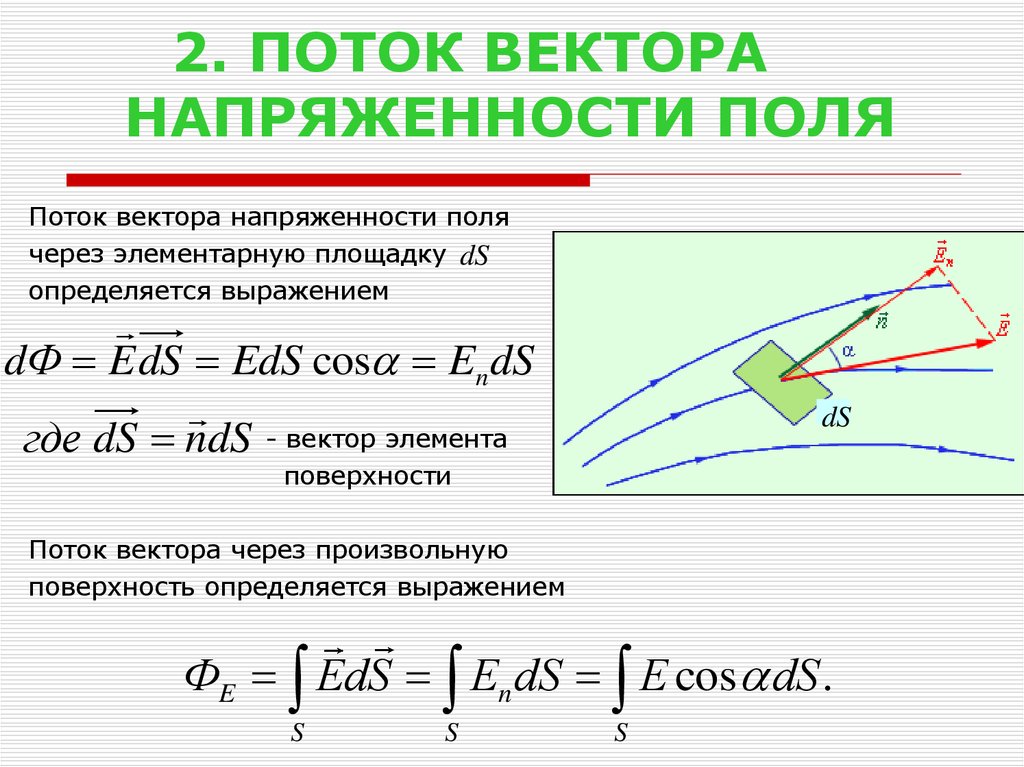
7. 2. ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ПОЛЯ
Поток вектора напряженности полячерез элементарную площадку dS
определяется выражением
dФ E dS EdS cos En dS
где dS ndS - вектор элемента
dS
поверхности
Поток вектора через произвольную
поверхность определяется выражением
ФE EdS En dS E cos dS .
S
S
S
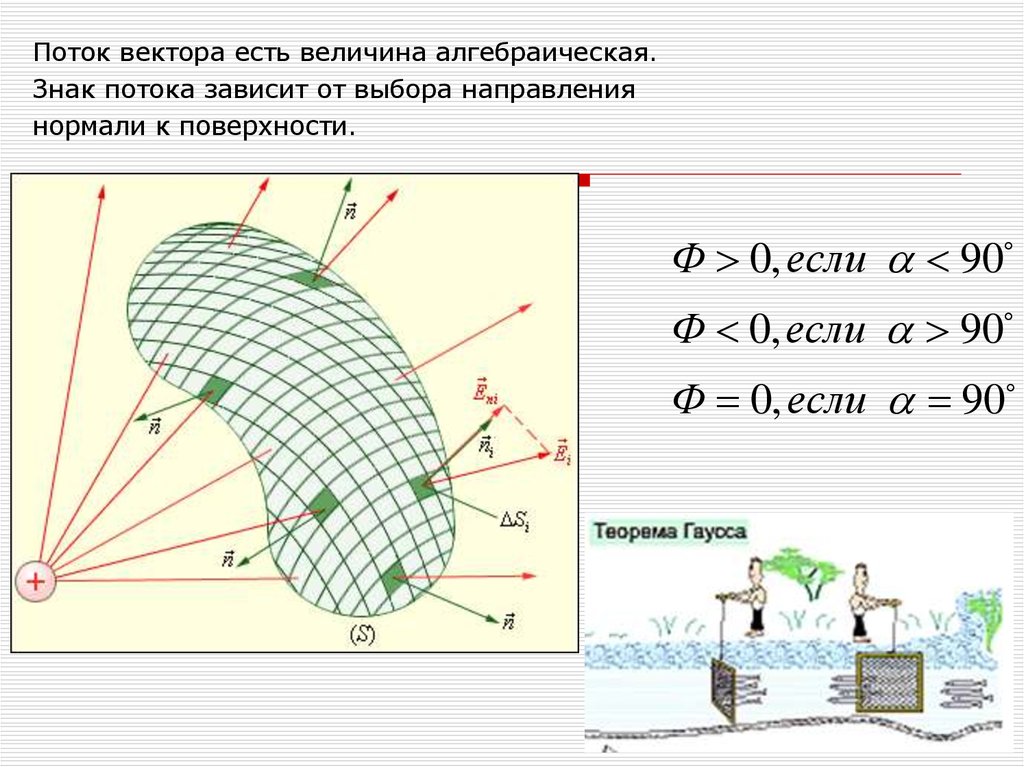
8.
Поток вектора есть величина алгебраическая.Знак потока зависит от выбора направления
нормали к поверхности.
Ф 0, если 90
Ф 0, если 90
Ф 0, если 90
9. 3. ТЕОРЕМА ГАУССА
Поток вектора напряженности электростатического полясквозь любую замкнутую поверхность равен алгебраической
сумме зарядов, находящихся внутри этой поверхности, деленной
на 0.
1
E dS
S
0
q
i
1. Теорема Гаусса устанавливает фундаментальное
свойство ЭП – наличие у него источников (+ заряды) (и
стоков (- заряды)) линий поля.
2. Теорема Гаусса позволяет вычислять
напряженность поля систем дискретно и непрерывно
распределенных зарядов, т.е. выступает аналогом закона
Кулона и принципа суперпозиции.
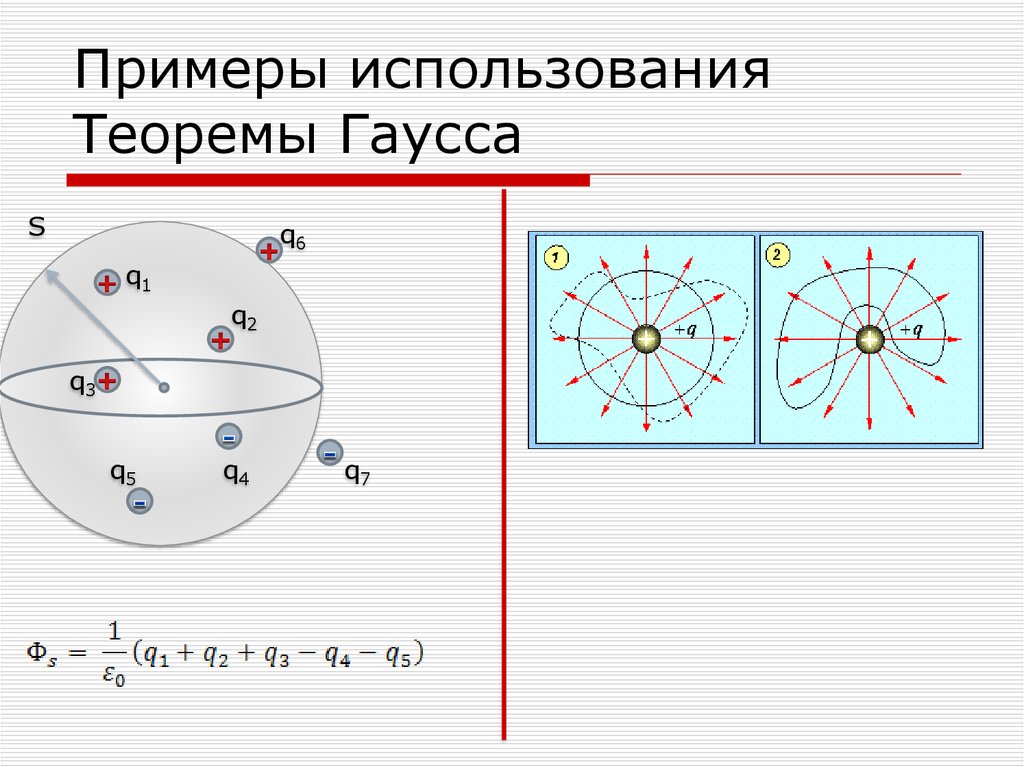
10. Примеры использования Теоремы Гаусса
Sq6
q1
q2
q3
q5
q4
q7
11. Примеры вычислений полей заряженных тел простых симметрий 4. Поле заряженной сферы
r R q r q0Er r 4 r 2
q0
0
q0
E (r )dS
r
S
0
1 q0
Er r
.
2
4 0 r
q0
(r ) ( ) k 2 dr; ( ) 0
r
r
dr
kq0
1
(r ) kq0 2 kq0
.
r
r
r r
r
kq0
(r)
.
r
12. ПОЛЕ ЗАРЯЖЕННОЙ СФЕРЫ
rR q r 0 E dS 0
S
Er r const Er (r ) dS 0
E (r )dS 0
r
S
Er (r ) 0.
S
R
r R Er r dr 0 (r ) ( R) 0 .
r
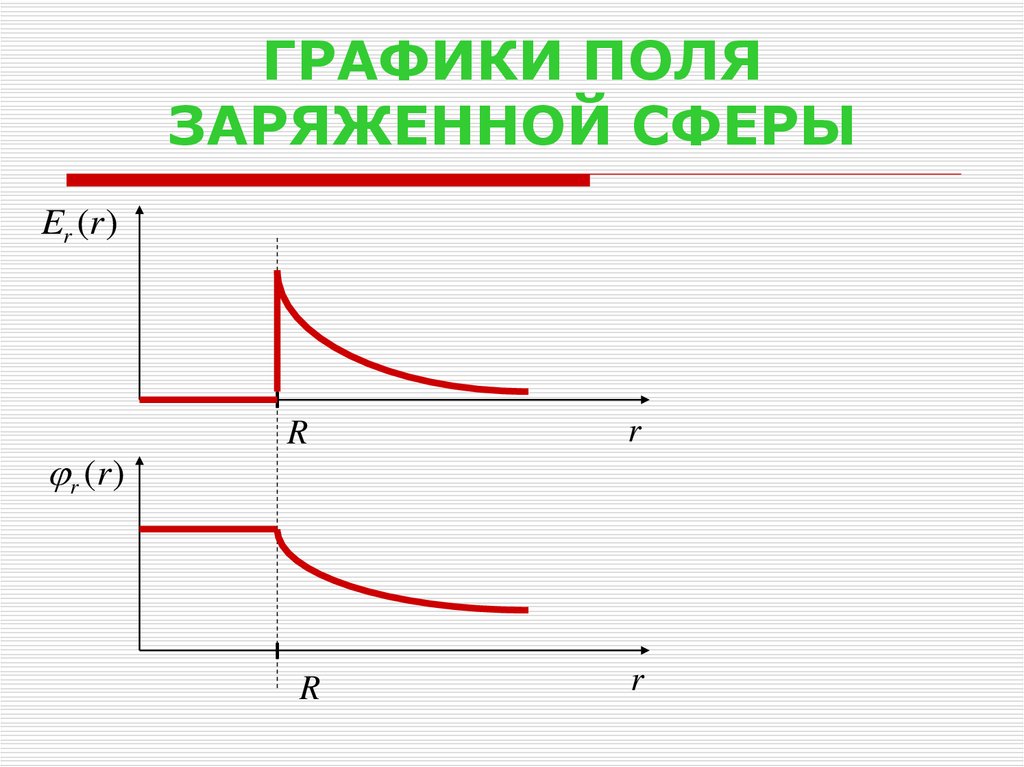
13. ГРАФИКИ ПОЛЯ ЗАРЯЖЕННОЙ СФЕРЫ
Er (r )r (r )
R
R
r
r
14. 4*. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ШАРА (I)
4 3q0
3q0
r R q(r ) r ;
3
V0 4 R
3
3
3q0 4 3
r
q(r )
q(r )
r
q
.
;
0
EdS
3
4 R 3
R
0
3
q0 r
EdS Er (r )dS Er (r )dS
0 R
3
q0 r
Er (r ) dS ;
0 R
3
q0 r
2
2
dS 4 r Er (r )4 r 0 R
R
kq0
kq0 2 2
1 q0 r
Er ( r )
. (r ) ( R) 3 rdr 3 ( R r ).
3
R r
2R
4 0 R
15. 4*. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ШАРА (II)
q(r ) q0r R
EdS Er (r )dS
EdS
Er (r ) dS
q0
0
q0
0
;
1 q0
q0
k 2.
Er (r )4 r Er (r )
2
4 0 r
r
0
2
q0
(r ) ( ) Er (r )dr;
( ) 0
r
dr
(r ) kq0 2
r
r
kq0
1
kq0
.
(r ) kq0
. 0 ( R )
R
r
r r
kq0 2 2
kq0 kq0 kq0 2 (0) 3 kq0 .
r R (r ) ( R) 3 ( R r )
3r .
2 R
2R
R 2R 2R
16. ГРАФИКИ ПОЛЯ равномерно ЗАРЯЖЕННОГО ШАРА
Er (r )r (r )
R
R
r
r
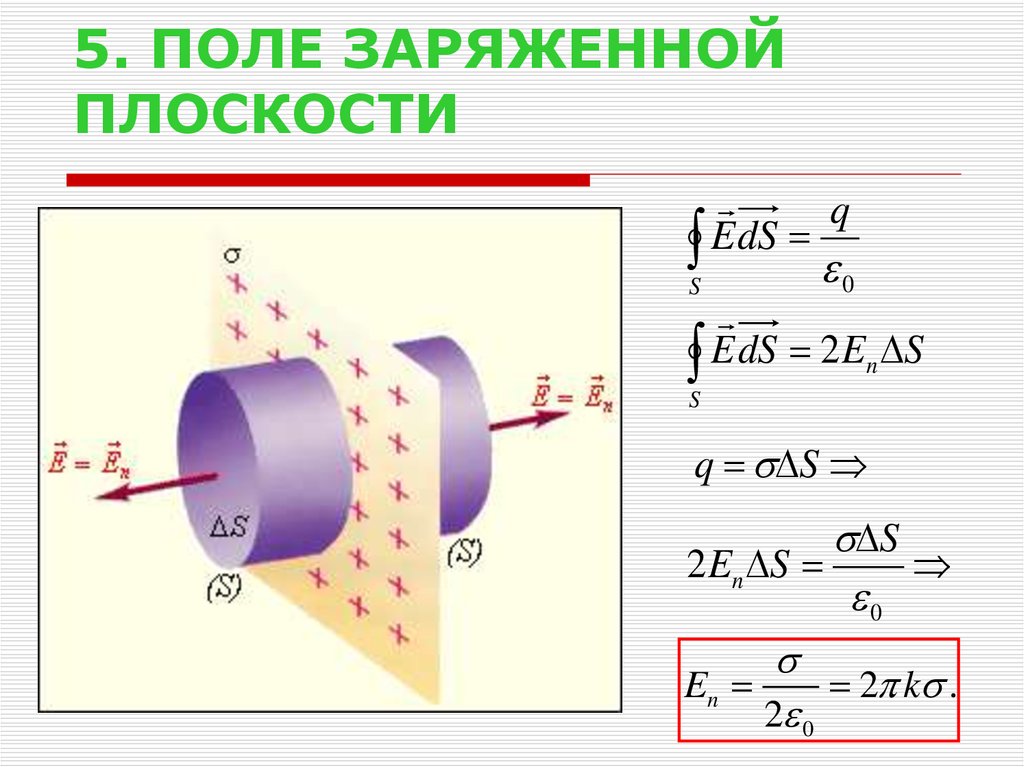
17. 5. ПОЛЕ ЗАРЯЖЕННОЙ ПЛОСКОСТИ
qE dS
S
0
E dS 2 En S
S
q S
S
2 En S
0
En
2 k .
2 0
18.
Разность потенциалов в поле равномерно заряженнойбесконечно протяженной плоскости
Поскольку поле однородно и направлено параллельно оси
ОХ, то потенциал поля зависит только от координаты Х
E
2 0
2 o
0 Edx E
.
2 0
0
E
х
2 o
x
19.
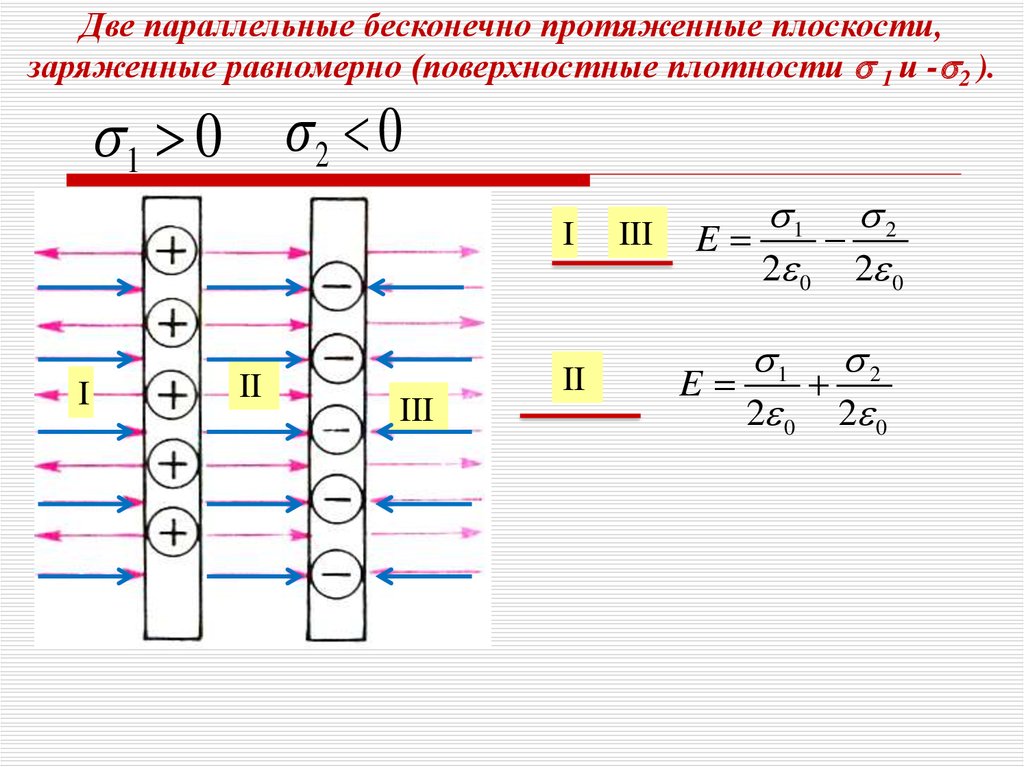
Две параллельные бесконечно протяженные плоскости,заряженные равномерно (поверхностные плотности 1 и - 2 ).
1 0 2 0
I
I
II
II
III
III
1 2
E
2 0 2 0
1 2
E
2 0 2 0
20.
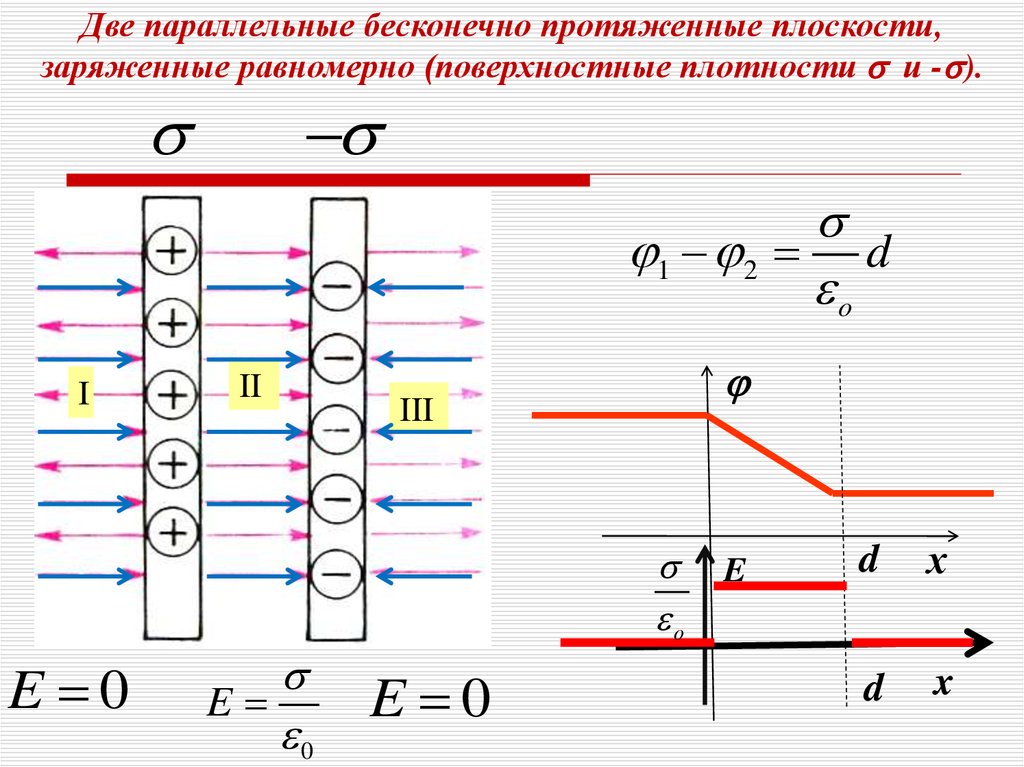
Две параллельные бесконечно протяженные плоскости,заряженные равномерно (поверхностные плотности и - ).
1 2 d
o
I
II
III
o
E 0
E
0
E 0
E
d
х
d
x
21. 6. ПОЛЕ ПОЛОГО ЦИЛИНДРА
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной плотностью заряда:l 2 Rl 2 R . R
r R Er (r ) 0. (r ) ( R) Er (r )dr 0.
l
S EdS 0
l
Er ( r ) dS
0
S
q(l ) l
r
r R q(l ) l
EdS Er (r )dS
dS 2 rl
S
dr
1
r
(
R
)
(
r
)
ln
Er
.
.
2 0 R r 2 0 R
2 0 r
r
22. 6+. ПОЛЕ ЗАРЯЖЕННОЙ ПРЯМОЛИНЕЙНОЙ НИТИ
Er ( r )1
2k
2 0 r
r
(r 0).
r2
dr
( r1 ) ( r2 ) Er dr 2k 2k ln .
r
r1
r1
r1
r2
r2
r2
( r1 ) ( r2 ) 2k ln
r1
23. 7. ТЕОРЕМА ОСТРОГРАДСКОГО - ГАУССА
Поток некоторого вектора через произвольную замкнутую поверхностьравен интегралу от дивергенции этого же вектора по объему,
ограниченному рассматриваемой поверхностью
E dS divEdV
S
Михаил Васильевич
Остроградский
1801 – 1862
русский математик
V
Карл Фридрих
Гаусс
1777 – 1855
немецкий математик
24. 8. ДИВЕРГЕНЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ПОЛЯ
Дивергенцией (divergentia – расхождение) векторного поля называетсявеличина, численно равная плотности точек (т.е. количеству точек в единице объема), в которых начинаются либо оканчиваются силовые линии
поля. Определение дивергенции имеет вид:
1
divE lim
E dS
V 0 V
S
ФE ( E x 2 E x1 ) y z ( E y 2 E y1 ) x z
( E z 2 E z1 ) x y
E y
E x
E z
ФE
x y z
y x z
z x y
x
y
z
x y z V
Ex E y Ez
E x E y E z
divE
E .
V
ФE
x
y
z
x
y
z
25. 9. ТЕОРЕМА ГАУССА в дифференциальной форме
1E dS
S
0
q
i
1
qi dV E dS
V
S
используем Т О-Г
dV
0 V
divE ;
divEdV
dV
;
V
0
0 V
1
div E
0
или
E .
0
26. 10. УРАВНЕНИЕ ПУАССОНА
E ; E0
divgrad ; ;
0
0
2
.
0
2
Симеон Дени Пуассон
1781 – 1840
французский математик
2
2
2
2
2 i
j k 2 2 2
y
z x y
z
x
оператор
Лапласа.
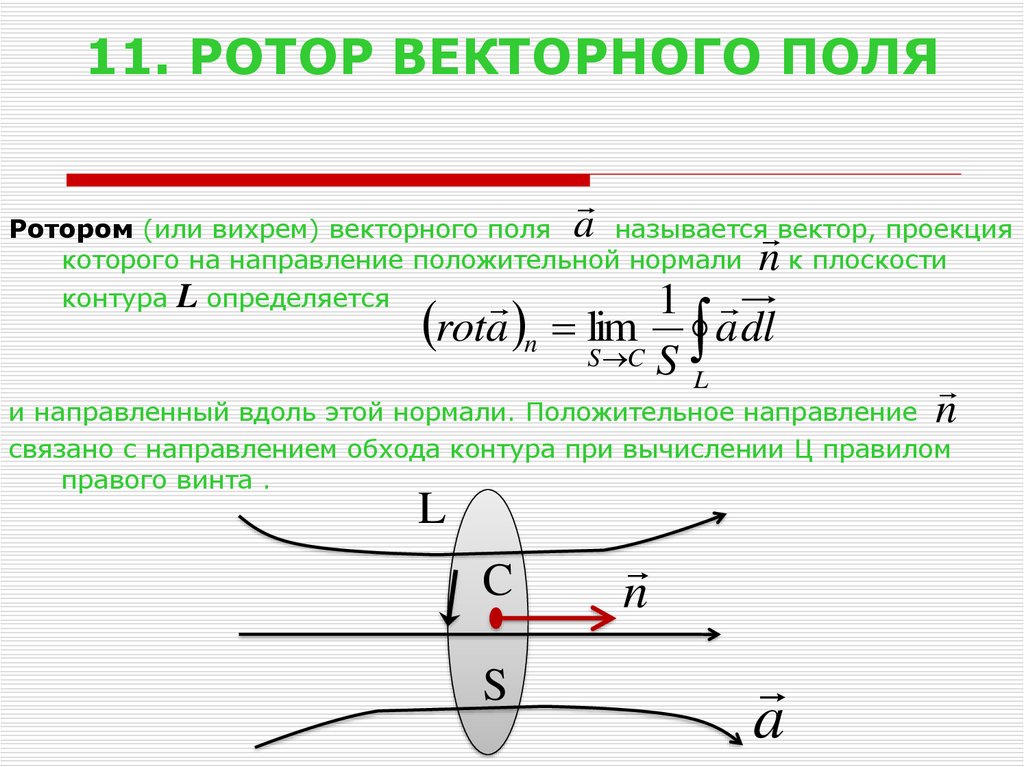
27. 11. РОТОР ВЕКТОРНОГО ПОЛЯ
an
Ротором (или вихрем) векторного поля
называется вектор, проекция
которого на направление положительной нормали
к плоскости
контура L определяется
1
rota n lim
a dl
S C S
L
n
и направленный вдоль этой нормали. Положительное направление
связано с направлением обхода контура при вычислении Ц правилом
правого винта .
L
C
S
n
a
28. 12. ТЕОРЕМА СТОКСА. РОТОР НАПРЯЖЕННОСТИ ПОЛЯ
Теорема Стокса. Циркуляция любого вектора по произвольномуконтуру равна потоку ротора этого же вектора через произвольную
поверхность, ограниченную данным контуром
E dl rotE dS
E dl 0
L
rotE dS 0
L
S
rotE E ;
rotE 0
E 0
S
теорема о Ц в диф. форме
i
j
k
Ex
Ey
Ez
.
i
j k E
x y z
x
y
z
29. 13. ОСНОВНЫЕ ТЕОРЕМЫ ЭП В ВАКУУМЕ
ТЕОРЕМА ГАУССАИФ
1
E dS
S
ДФ
ТЕОРЕМА О
ЦИРКУЛЯЦИИ
E dl 0
dV
0 V
E .
0
L
E 0


















 physics
physics








