RC&Masonry

1.

Моделирование нелинейной
работы железобетонных и
каменных конструкций

2.

Поведение изгибаемых железобетонных элементов
Бетон: Rb=29 МПа, Rbt=5 МПа, εult,c=130x10-5, εult,t=65x10-5, Еb=1.56х107 кПа
Арматура: Rs=538 МПа, Es=2.06x108 кПа, εult,s=2000x10-5

3.

СП 63.13330.2018

4.

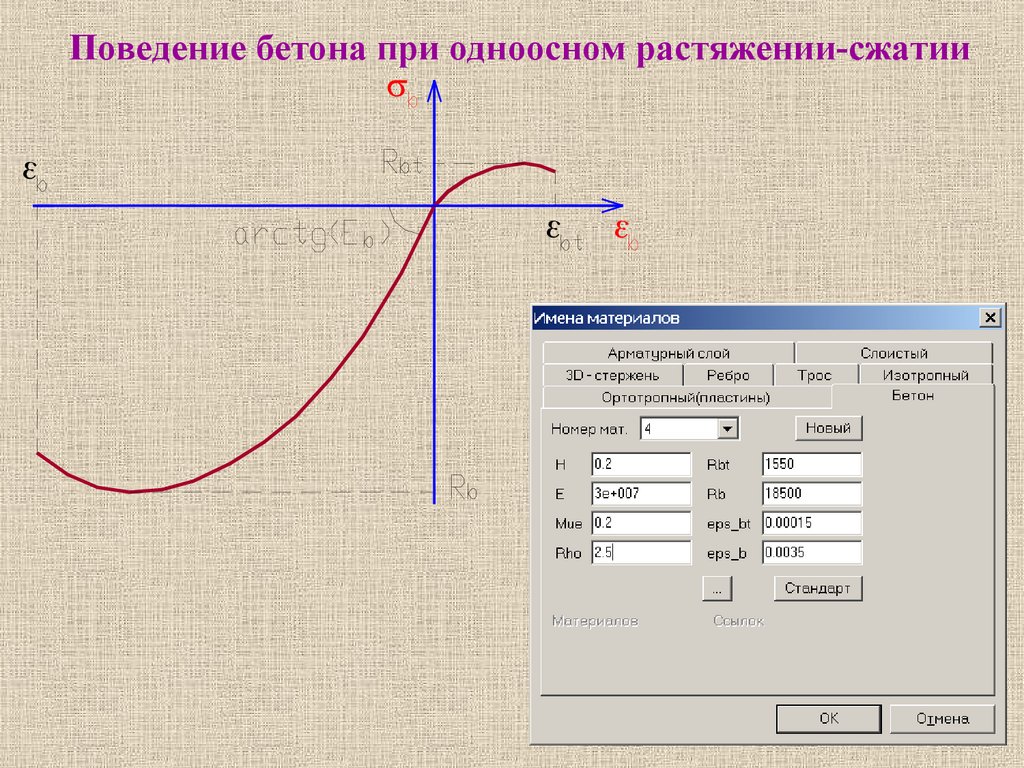
Поведение бетона при одноосном растяжении-сжатии

5.

Ф12 AIII (мягкая сталь)
800
700
600
500
Образец №1
Образец №2
Образец №3
400
300
200
100
0
0
1000
2000
3000
4000
5000
s , МПа
s , МПа
Поведение арматурной стали при растяжении
6000
7000
e *105
Ф12 Ат-V
1400
1200
1000
800
Образец №1
Образец №2
600
400
200
0
0
1000
2000
3000
4000
e *105
5000

6.

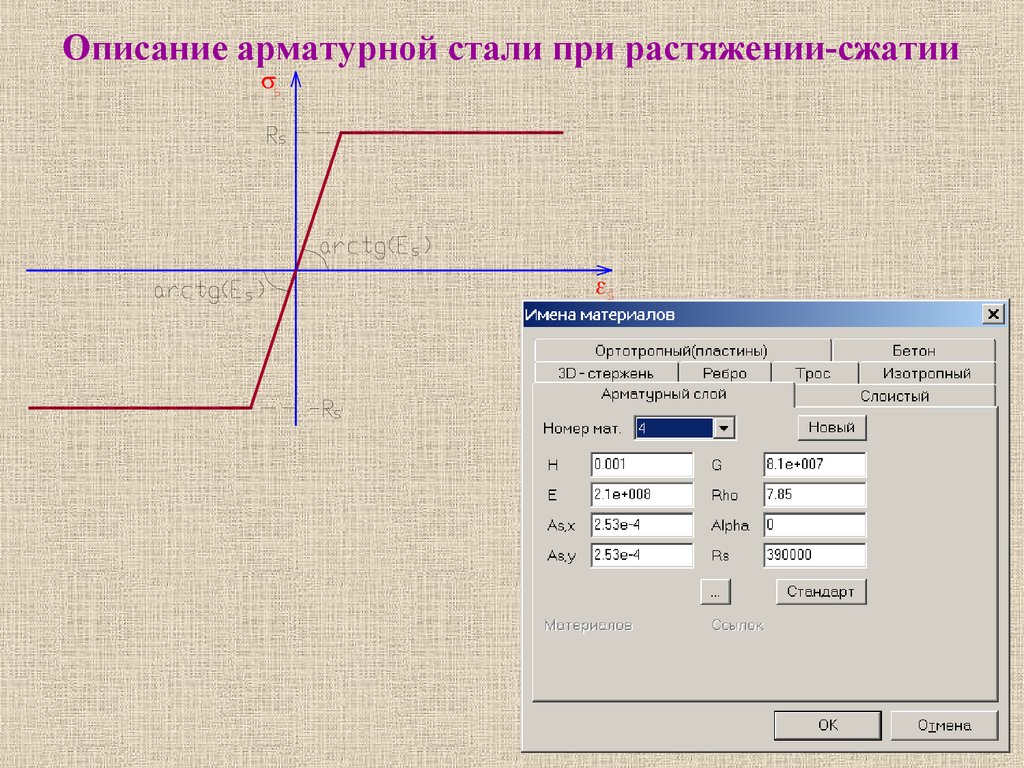
Описание арматурной стали при растяжении-сжатии

7.

Поведение кирпичной кладки при изгибе в своей плоскости
P , kN
12
10
образец 1.1-1
образец 1.1-2
образец 1.1-3
8
6
4
2
0
0
0.1
0.2
0.3
0.4
0.5
Прогибы под точками приложения нагрузки, мм

8.

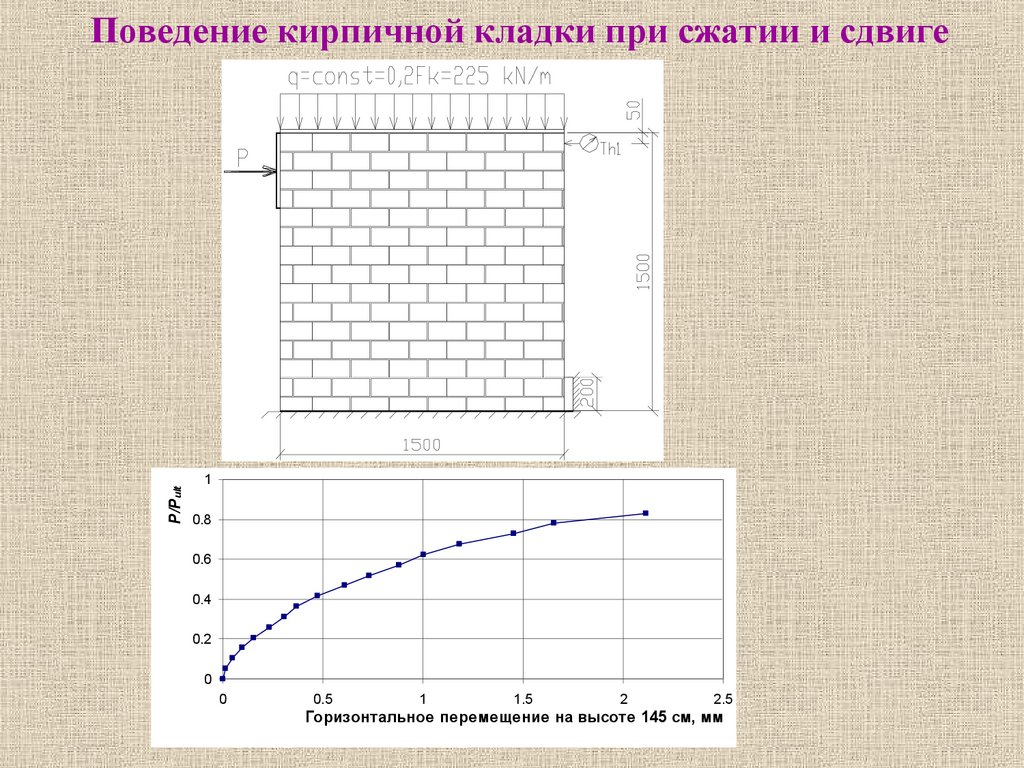
P/Pult
Поведение кирпичной кладки при сжатии и сдвиге
1
0.8
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
Горизонтальное перемещение на высоте 145 см, мм

9.

Разрушение кирпичной кладки при сжатии и сдвиге
При большом обжатии
При малом обжатии

10.

Поведение кирпичной кладки при одноосном сжатии

11.

s / s ult
Поведение кирпичной кладки при одноосном сжатии
1
0.8
0.6
0.4
продольные
деформации
поперечные
деформации
0.2
0
-25
0
25
0.6
50
s / s ult
s / s ult
-50
0.5
0.4
75
0.6
0.5
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.05
0.1
0.15
0.2
n
0.25
100
125
5
e x10
7500
10000
12500
15000
17500
E sec, MPa

12.

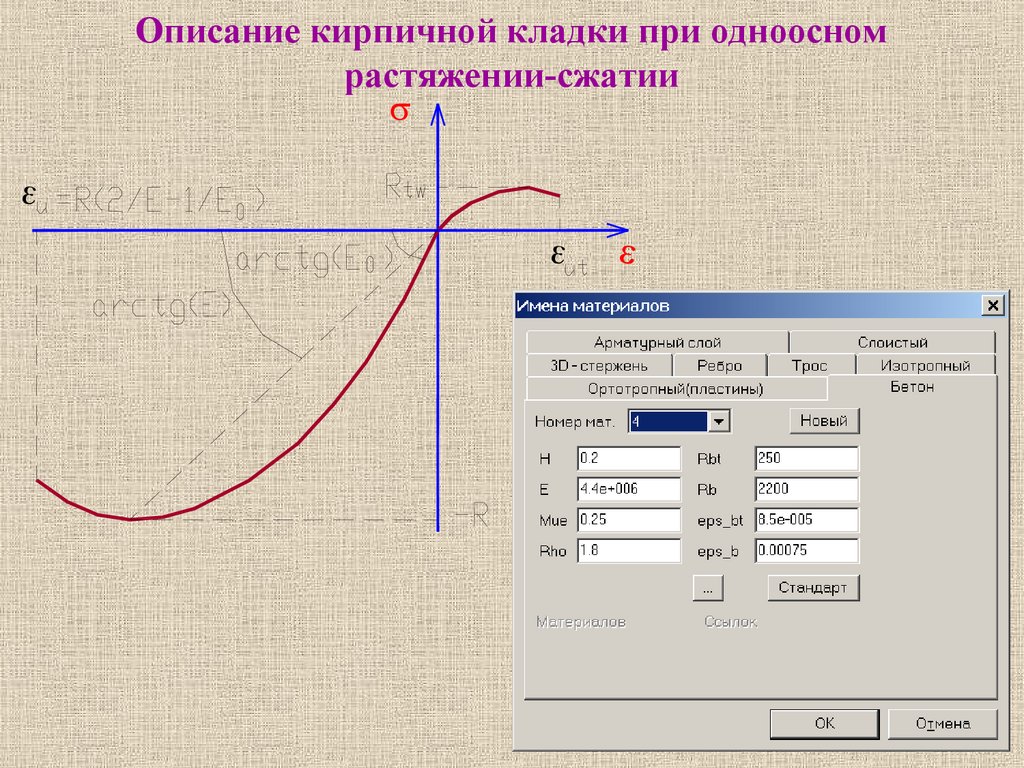
Описание кирпичной кладки при одноосном
растяжении-сжатии

13.

Нелинейные зависимости для железобетонных
элементов

14.

Нелинейные зависимости для железобетонных
2. Элемент пологой оболочки
элементов
1 о1 1 ( z z о1 ) ;
2 о 2 2 ( z z о 2 ) ,
1
2
zdA
zdA
A 1
,
A 2
z о1
zо2
;
1
2
dA
dA
A
A
1
2
где
1
2
1
2
1 о1 N 1 ;
B M 1 ;
1
1
2 о 2 N 2 ;
B2 2 M 2 ;
si,1 f si,1 ( si,1 ) ;
si, 2 f si, 2 ( si, 2 ) ;
c1 f c ( c1 , c 2 ) ; c 2 f c ( c 2 , c1 ) ,
где 1 1 dA ; B1 1 ( z z о1 ) 2 dA ;
1
A 1
A
1
1
2 2 dA ; B2 2 ( z z о 2 ) 2 dA .
2
A 2
A
2
2

15.

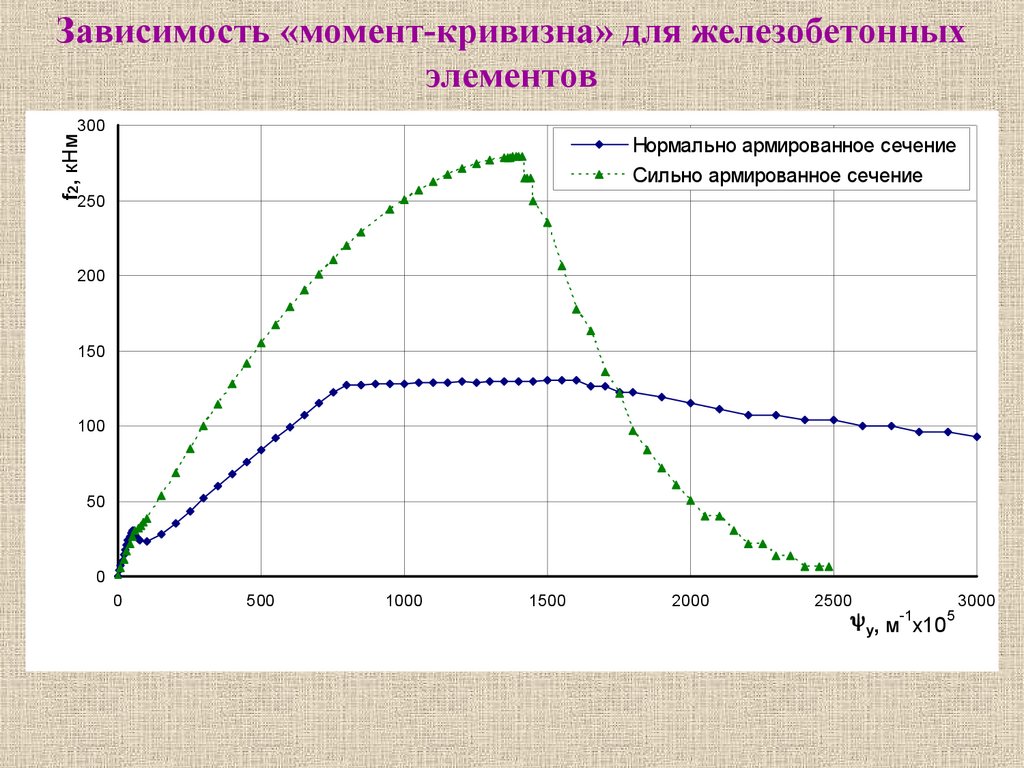
Зависимость «момент-кривизна» для железобетонных
элементов
300
f2, кНм
Нормально армированное сечение
Сильно армированное сечение
250
200
150
100
50
0
0
500
1000
1500
2000
2500
y y, м х10
-1
5
3000

16.

Упражнение. Расчет прогиба железобетонной плиты
Имеется расчетная модель
железобетонной плиты,
представленной линейными
изотропными элементами
(Slab0.fea), известно продольное
армирование плиты.
Требуется выполнить физически
и геометрически нелинейный
расчет плиты с учетом
трещинообразования и
ползучести бетона с целью
контроля ее прогибов при
действии нормативной
постоянной и длительной
нагрузки.

17.

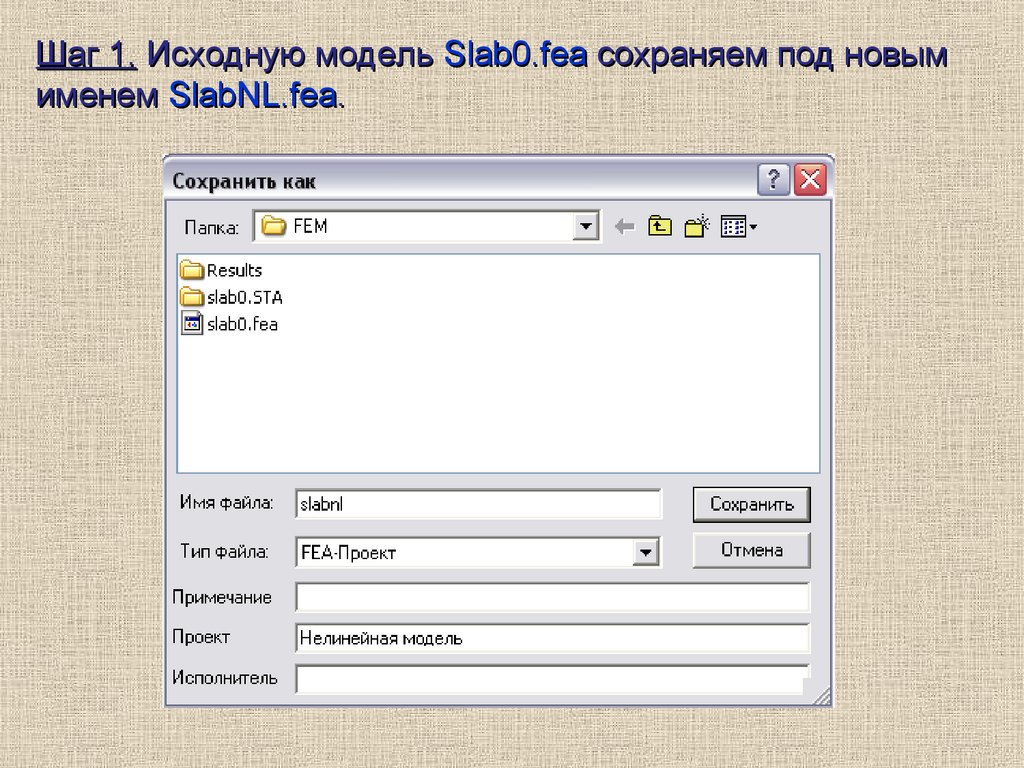
Шаг 1. Исходную модель Slab0.fea сохраняем под новым
именем SlabNL.fea.

18.

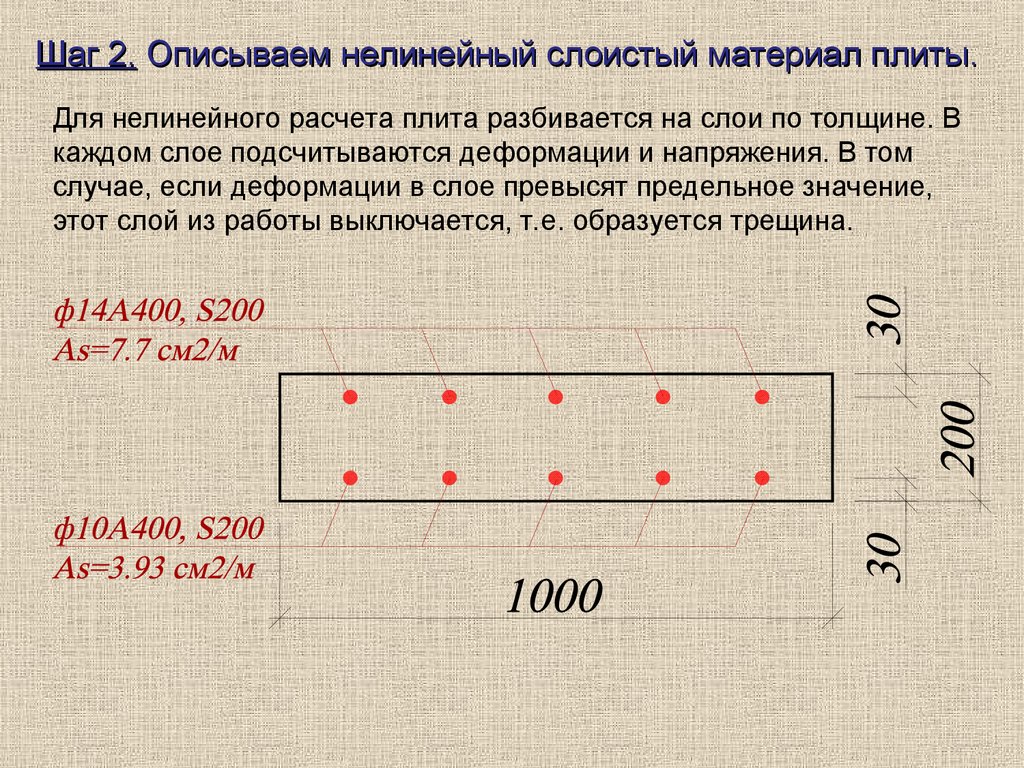
Шаг 2. Описываем нелинейный слоистый материал плиты.
Для нелинейного расчета плита разбивается на слои по толщине. В
каждом слое подсчитываются деформации и напряжения. В том
случае, если деформации в слое превысят предельное значение,
этот слой из работы выключается, т.е. образуется трещина.

19.

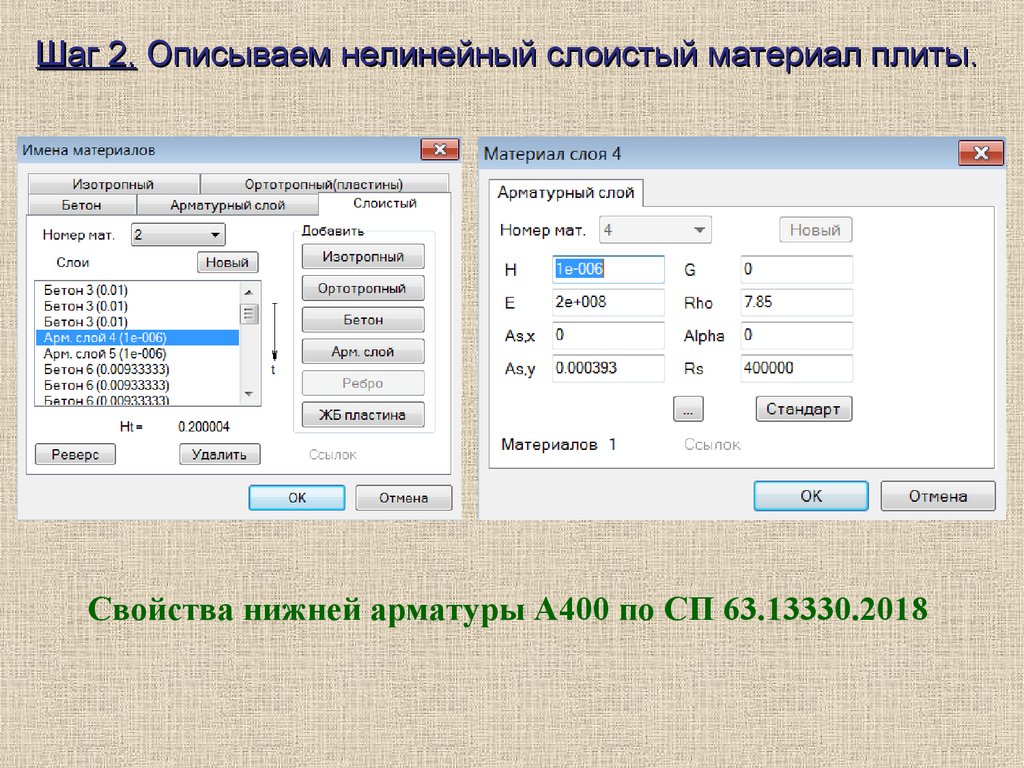
Шаг 2. Описываем нелинейный слоистый материал плиты.

20.

Шаг 2. Описываем нелинейный слоистый материал плиты.
Свойства бетона В25 при длит. нагрузке по СП 63.13330.2018

21.

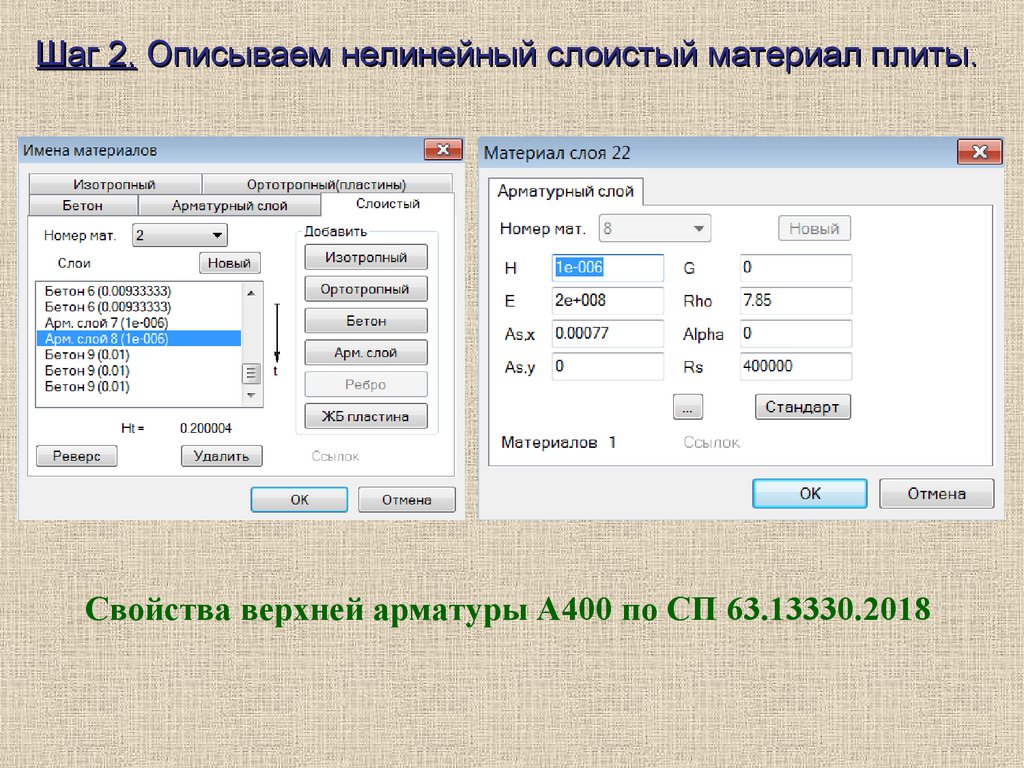
Шаг 2. Описываем нелинейный слоистый материал плиты.
Свойства верхней арматуры А400 по СП 63.13330.2018

22.

Шаг 2. Описываем нелинейный слоистый материал плиты.
Свойства нижней арматуры А400 по СП 63.13330.2018

23.

Шаг 3. Присваиваем нелинейный слоистый материал
элементам плиты.

24.

Шаг 4. Задаем комбинацию нормативных постоянных и
длительных нагрузок.
1.0:1.2
0.35:1.2
Для перевода расчетных полных нагрузок в нормативные
длительные используем коэффициенты для нагружений, равные
отношению Кд/Кн (к-тов длительности и надежности по нагрузке).

25.

Шаг 5. Выполняем статический расчет при следующих
установках:
Учет геометрической нелинейности
Учет физической нелинейности

26.

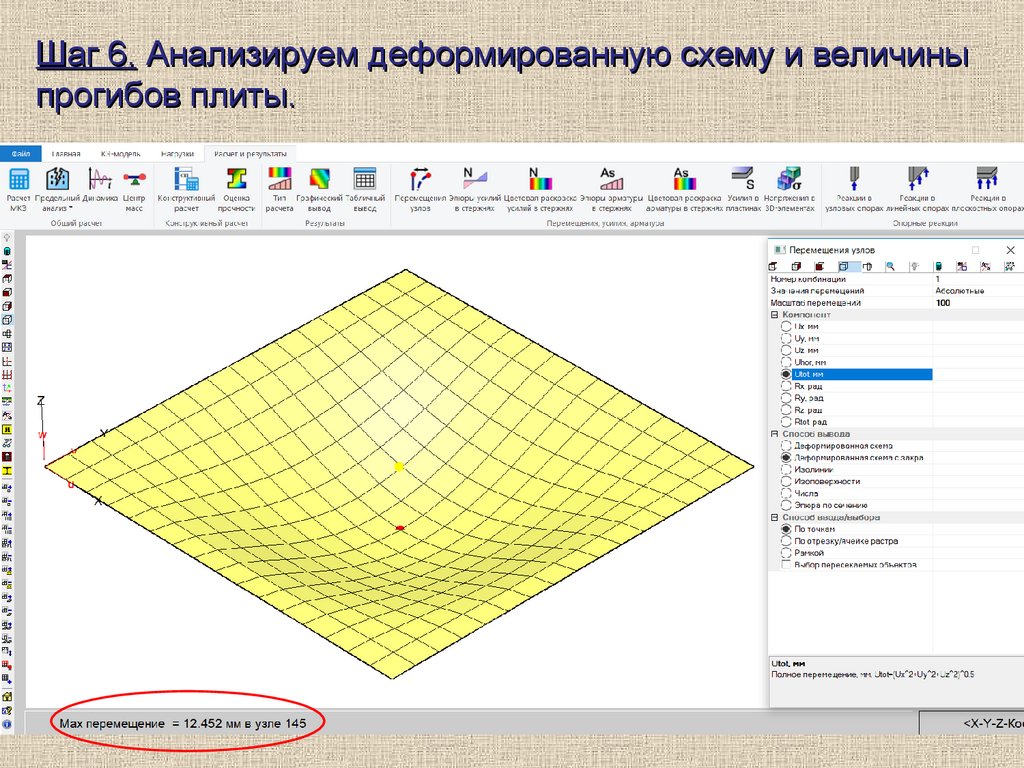
Шаг 6. Анализируем деформированную схему и величины
прогибов плиты.