Методы выбора и принятия решений

1. Тема. Методы выбора и принятия решений

1. Классификация задач выбора.
2. Критериальный язык описания
выбора.
Сведение многокритериальной задачи к
однокритериальной. Условная максимизация. Нахождение паретовского множества.
3. Описание выбора на языке
бинарных отношений.
Способы задания бинарных отношений.
Отношения эквивалентности, порядка и
доминирования. Функция полезности.

2. Тема. Методы выбора и принятия решений

4. Выбор в условиях статистической
неопределенности.
Общая схема принятия статистических
решений. Понятие о байесовом подходе.
5. Выбор в условиях неопределенности.
Платежная матрица. Максиминный критерий.
Критерии Сэвиджа, Гурвица.
6. Выбор на нечетком множестве
альтернатив.
Нечеткие множества целей, ограничений,
решений.

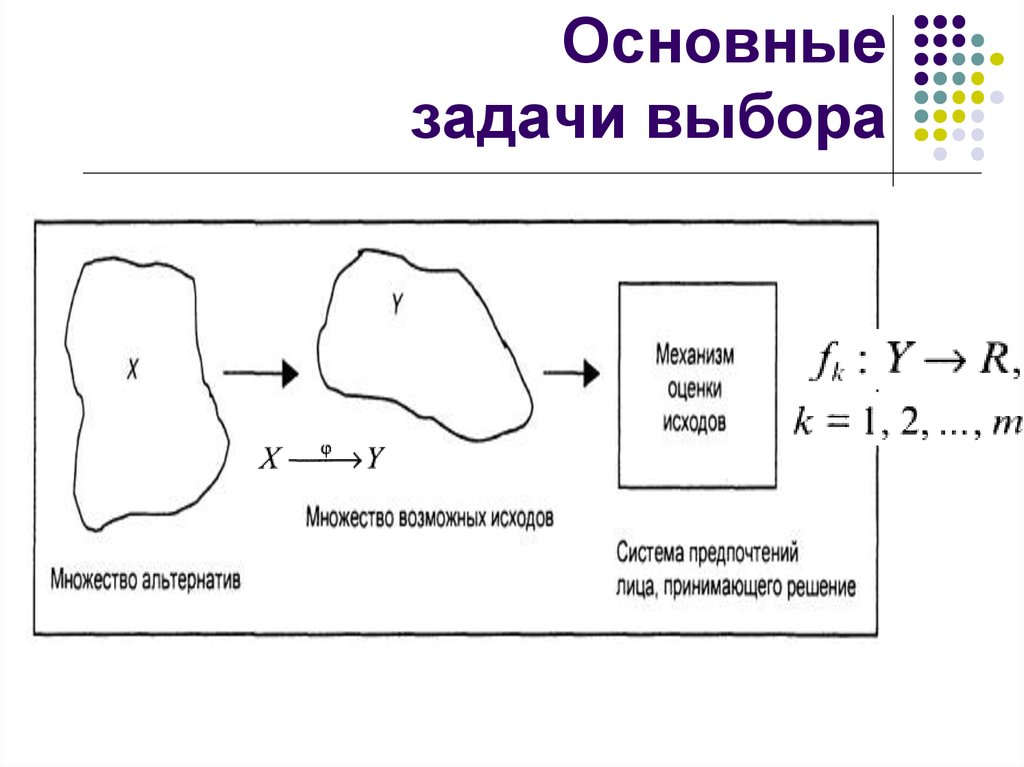
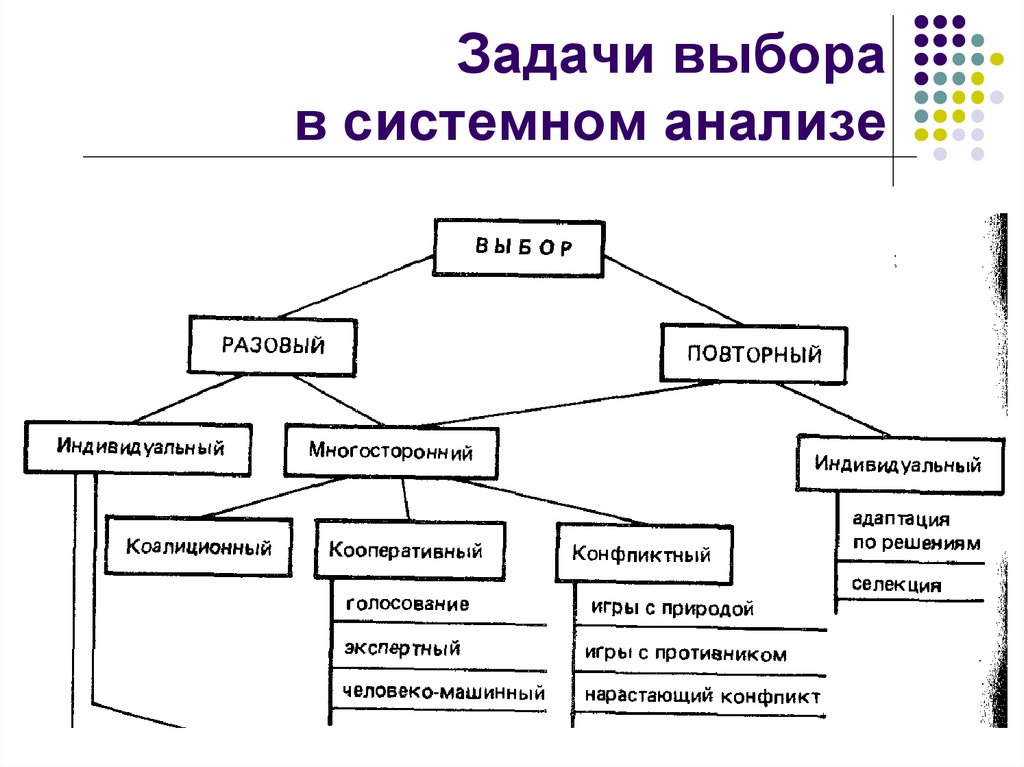
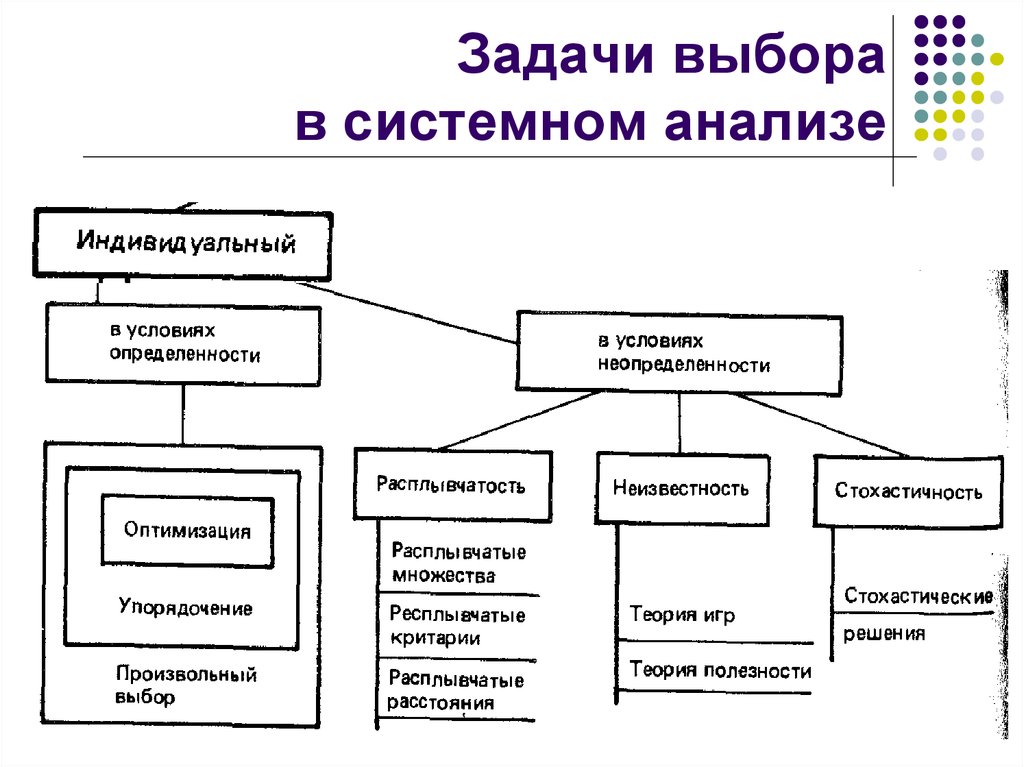
3. Основные задачи выбора

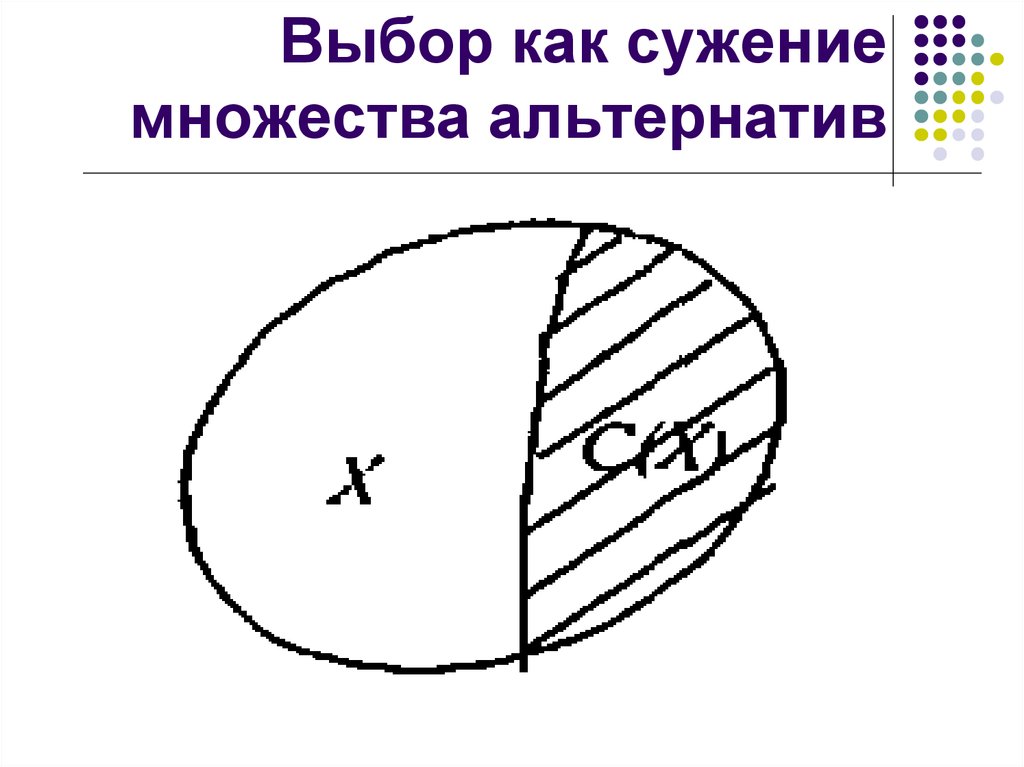
4. Выбор как сужение множества альтернатив

5. Основные задачи выбора

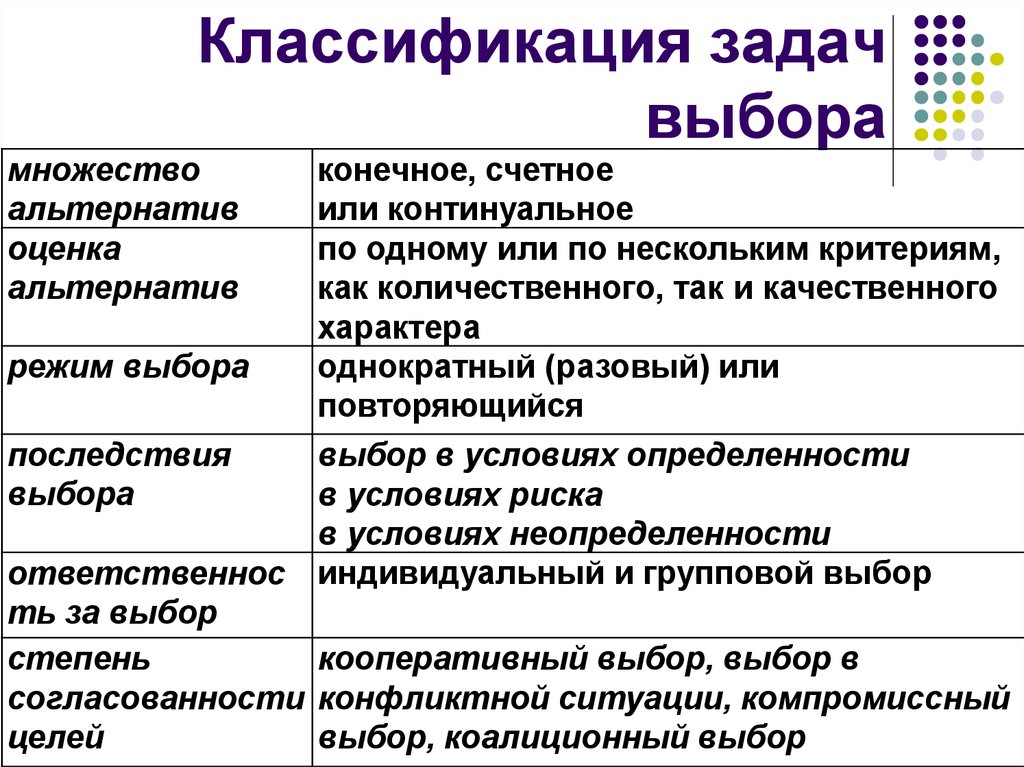
6. Классификация задач выбора

множество
альтернатив
оценка
альтернатив
конечное, счетное
или континуальное
по одному или по нескольким критериям,
как количественного, так и качественного
характера
режим выбора
однократный (разовый) или
повторяющийся
последствия
выбор в условиях определенности
выбора
в условиях риска
в условиях неопределенности
ответственнос индивидуальный и групповой выбор
ть за выбор
степень
кооперативный выбор, выбор в
согласованности конфликтной ситуации, компромиссный
целей
выбор, коалиционный выбор

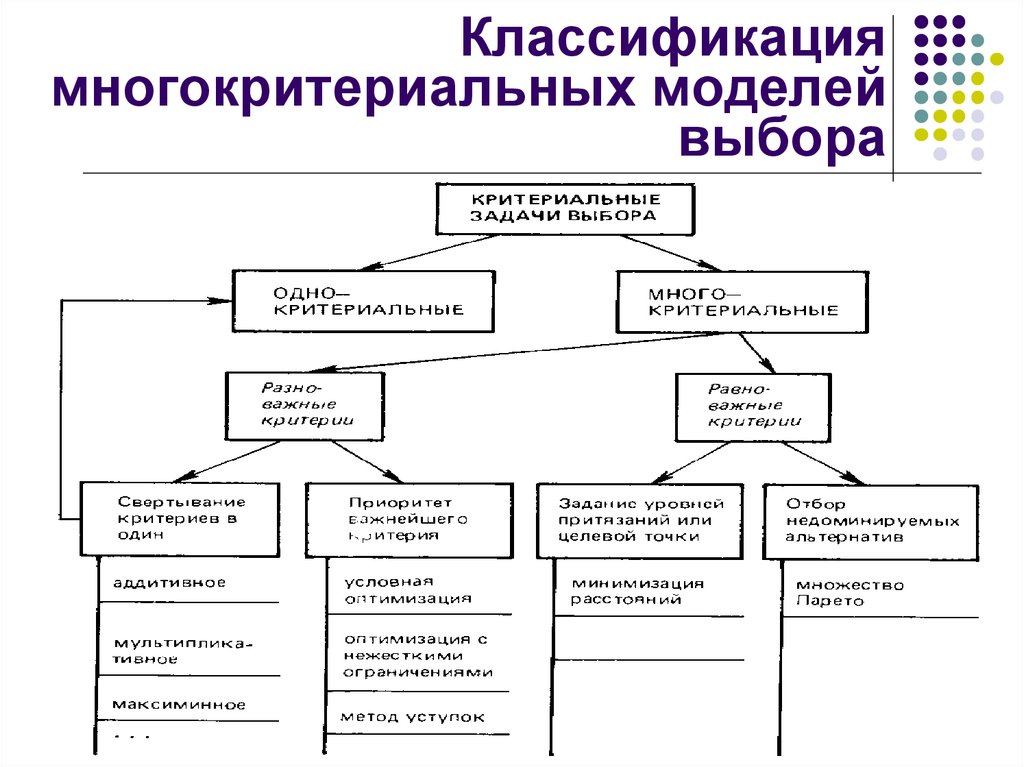
7. Постановка критериальной задачи выбора

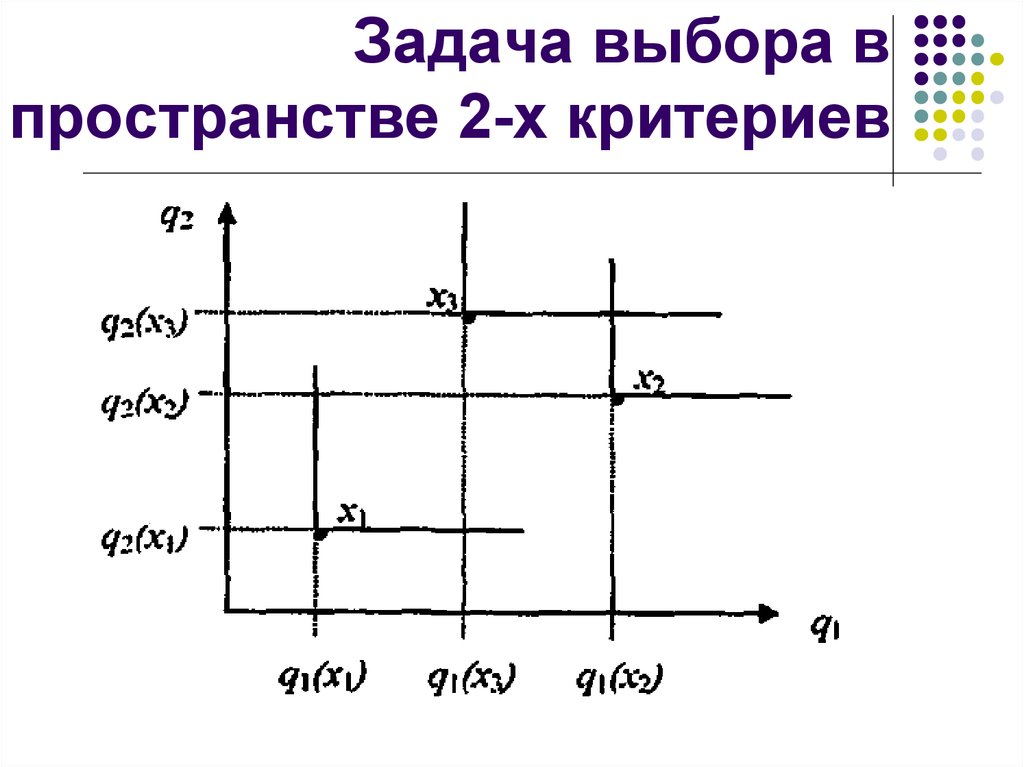
8. Задача выбора в пространстве 2-х критериев

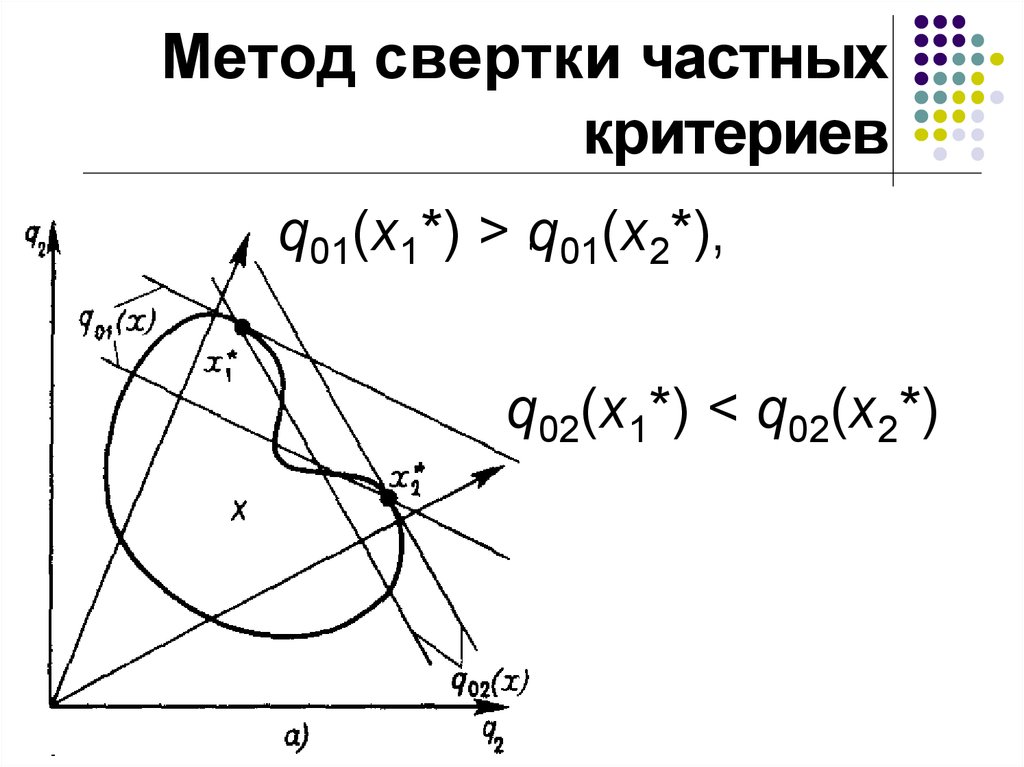
9. Метод свертки частных критериев

q0(x) = q0(q1(x), q2(x), ..., qp(x))
p
q0
i 1
i qi
;
si
x * arg max q0 ( q1 ( х ),..., q p ( х )).
x X

10. Метод свертки частных критериев

q01(x1*) > q01(x2*),
q02(x1*) < q02(x2*)

11. Метод условного экстремума основного критерия

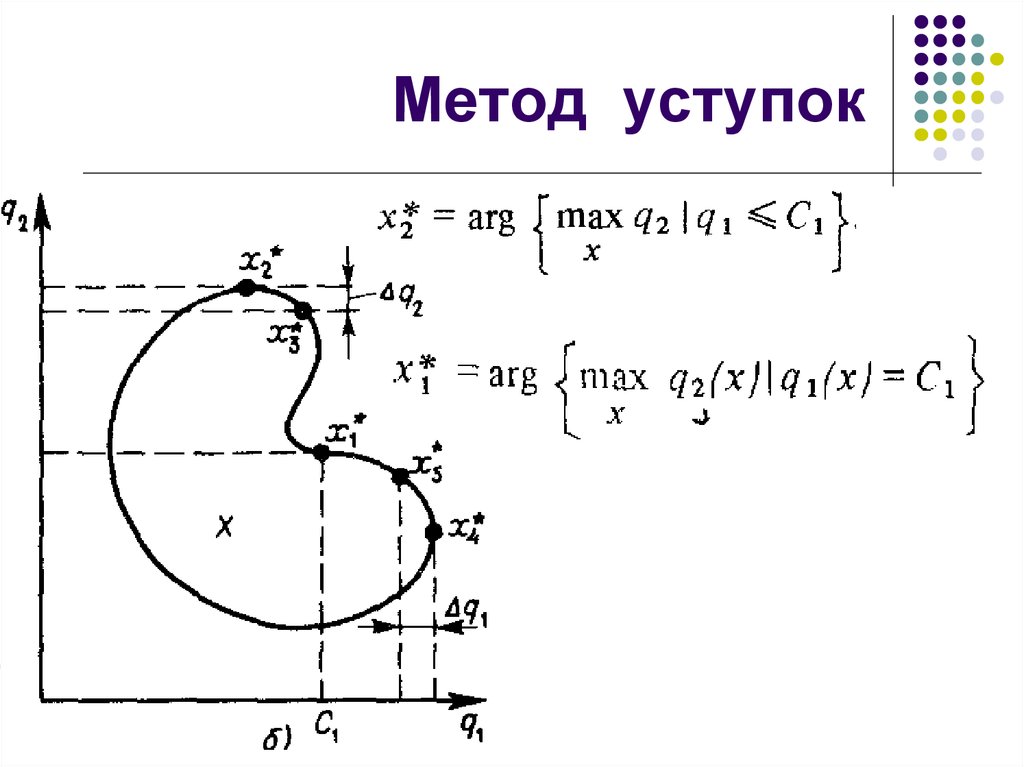
12. Метод уступок

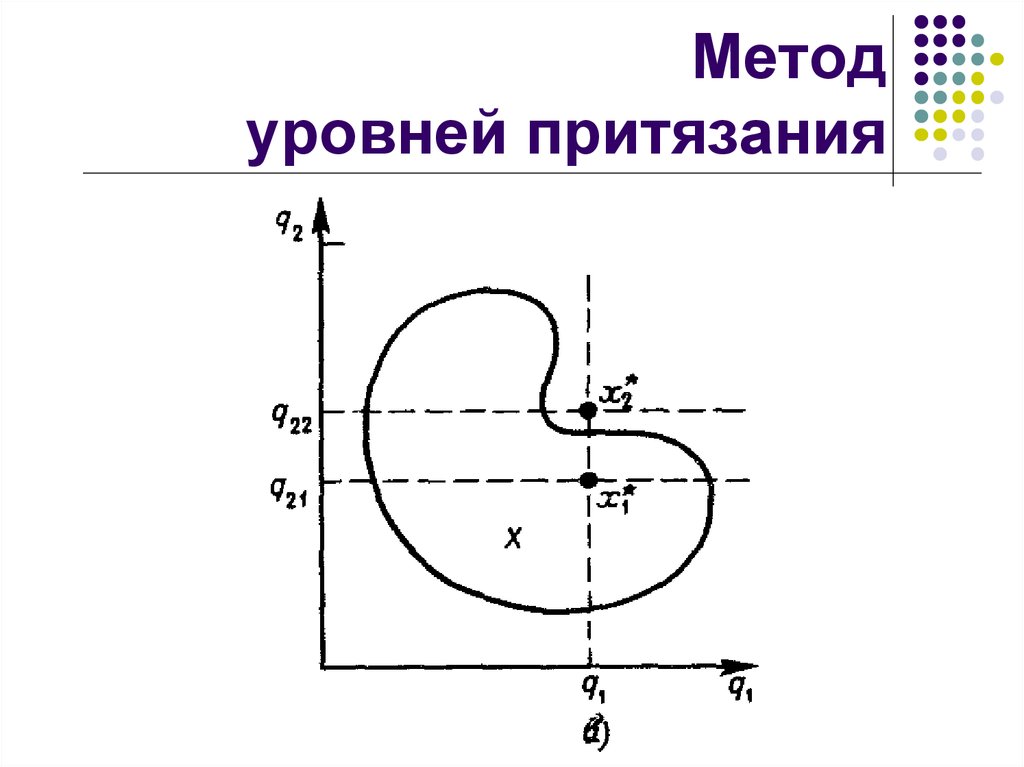
13. Метод задания опорных значений (уровней притязания)

Числовые меры близости (расстояние):

14. Метод уровней притязания

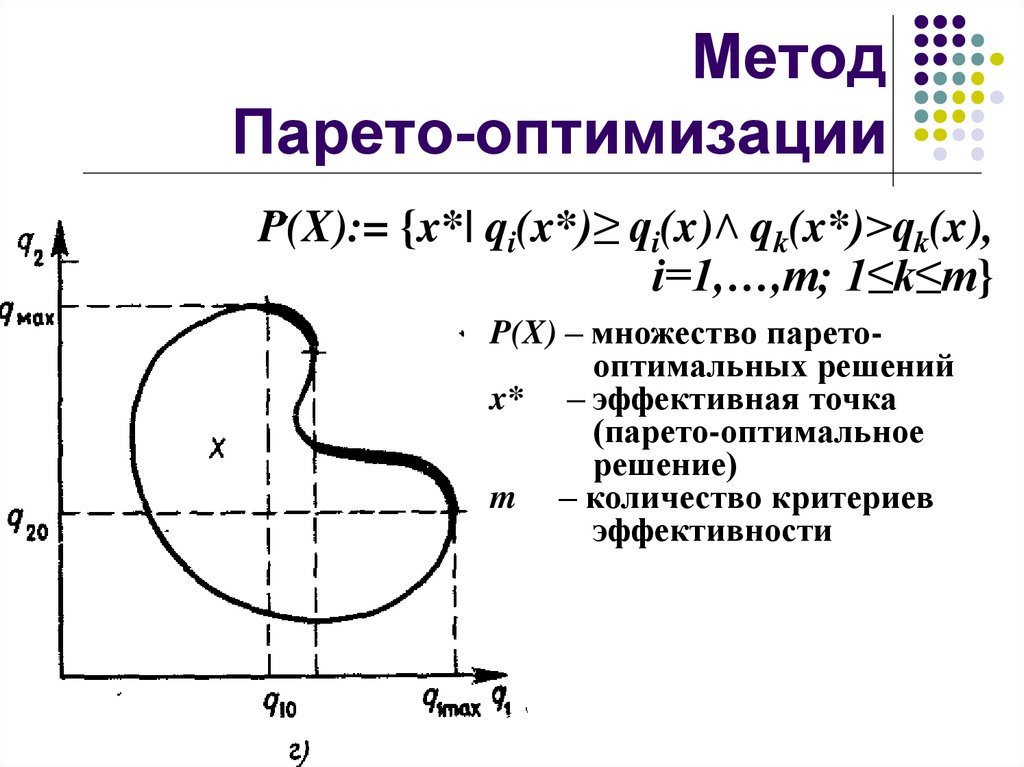
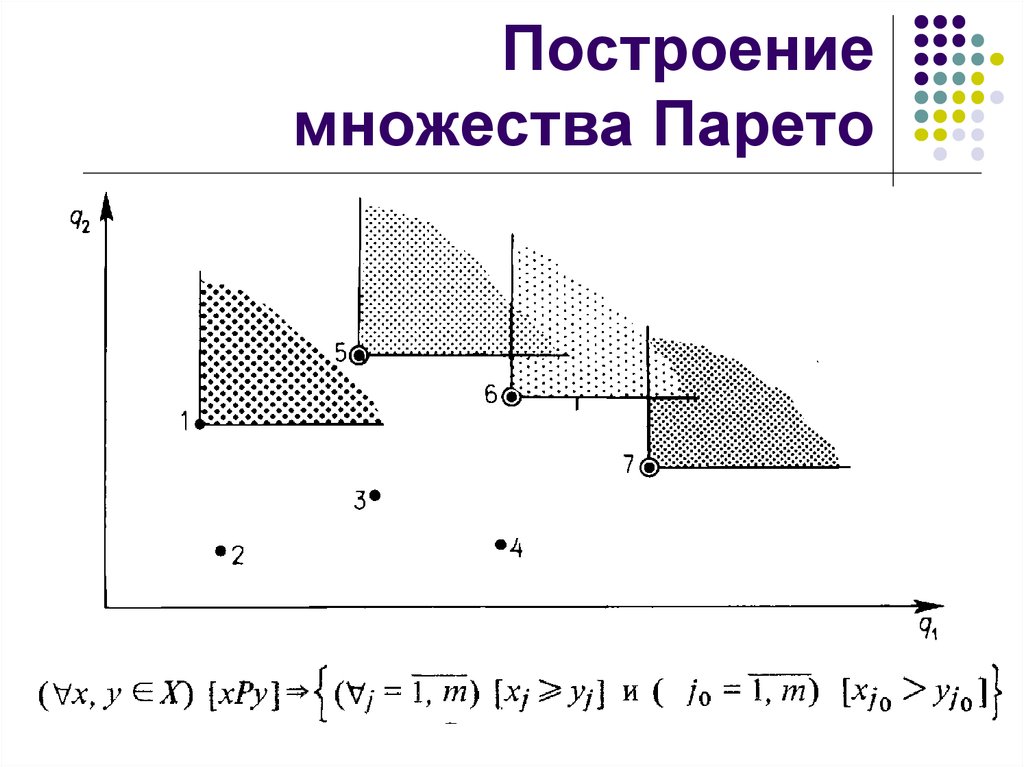
15. Метод Парето-оптимизации

P(X):= {x*| qi(x*)≥ qi(x)˄ qk(x*)˃qk(x),
i=1,…,m; 1≤k≤m}
P(X) – множество паретооптимальных решений
x* – эффективная точка
(парето-оптимальное
решение)
m – количество критериев
эффективности

16. Построение множества Парето

17. Классификация многокритериальных моделей выбора

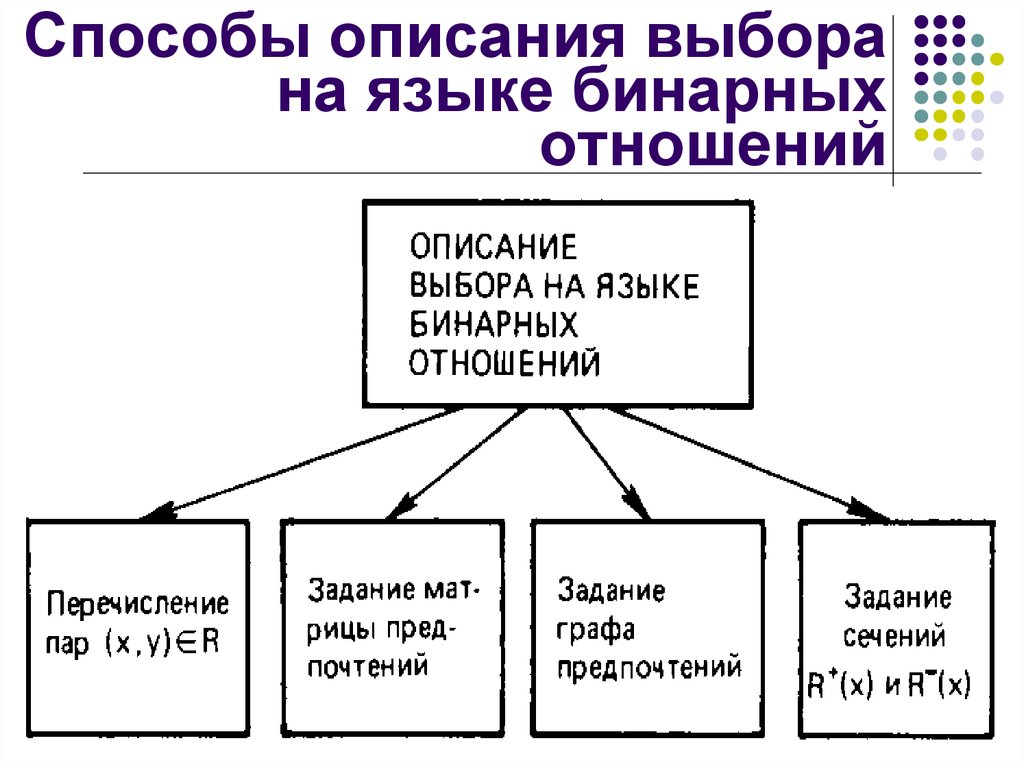
18. Способы описания выбора на языке бинарных отношений

19. Способы задания отношений на конечном множестве 

Способы задания
отношений на конечном
множестве

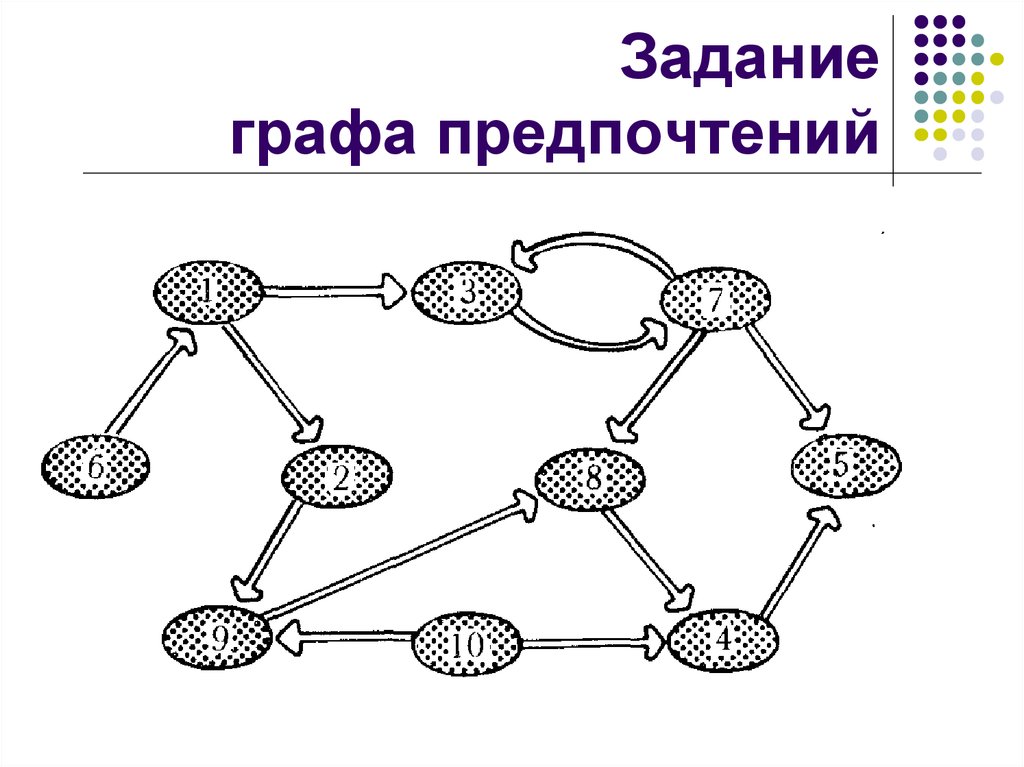
20. Задание графа предпочтений

21. Задание диагонального отношения E. Пример

1) в E входят только пары с
одинаковыми номерами: xi E xj
верно только при i = j;
2) aij(E) = { 1: i = j; 0: i ≠ j };
3) граф G(E) такой, что каждая его
вершина имеет петлю, а остальные
дуги отсутствуют;
4) R+(x) = R–(x) = x для любого x X.

22. Свойства бинарных отношений R на множестве X

23. Бинарные отношения на множестве альтернатив

Отношение эквивалентности (~):
Отношение нестрогого порядка ( )
рефлексивное, антисимметричное и транзитивное
Отношением строгого порядка (<)
рефлексивное, симметричное и транзитивное
антирефлексивное, асимметричное и транзитивное
Отношение доминирования
антирефлексивное и асимметричное

24. Функция полезности u(x)

u(x X): (x < y) [u(x) < u(y)]
u(x) - произвольное монотонное
преобразование, которое сохраняет
упорядочивающее свойство
множество X конечно
имеется отношение строгого
порядка на множестве X

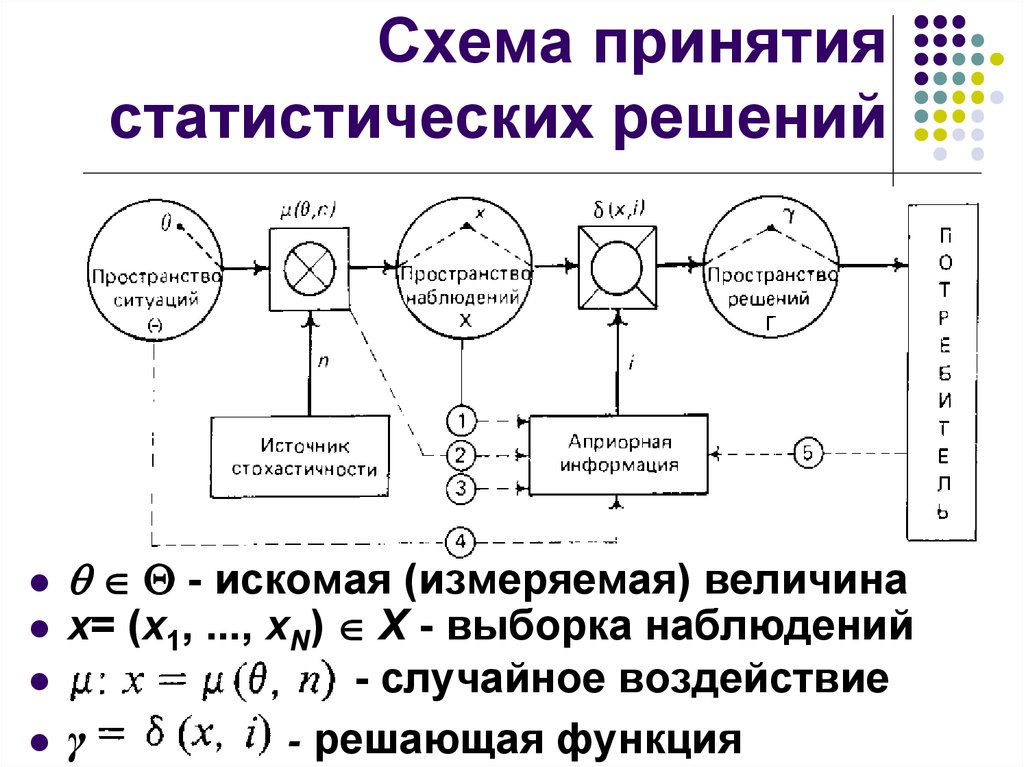
25. Схема принятия статистических решений

- искомая (измеряемая) величина
x= (x1, ..., xN) X - выборка наблюдений
- случайное воздействие
γ
- решающая функция

26. Байесов подход к выбору решений

*( x ) arg min R ( ( x )) arg min M X l( ( x ), )
( x )
( x )
arg min l( x ), dF ( x | ) dP ( ).
( x )
X
P( ), - функция распределения;
F(x| ), x X, - условное
распределение выборочных значений;
l(γ, ) - функция потерь l (γ, )
R - байесов риск

27. Формула Байеса

P(A) - априорная вероятность гипотезы A;
P(B|A) - вероятность гипотезы A при наступлении события B (апостериорная вероятность);
P(B|A) - вероятность наступления события
B при истинности гипотезы A;
P(B) - полная вероятность наступления
события B.

28. Платежная матрица игровых моделей

X\Y
x1
...
xi
...
xn
y1
q11
...
qi1
...
qn1
y2
q12
...
qi2
...
qn2
...
...
...
...
...
...
yj
q1j
...
qij
...
qnj
...
...
...
...
...
...
ym
q1m
...
qim
...
qnm
y = (y1, ...ym) – вектор возможных исходов
х = (х1, ...хn) – вектор альтернатив
qi = (qi1, ..., qim) – вектор “выигрышей”,
“потерь”, “платежей”

29. Критерии выбора в условиях неопределенности исходов

Максиминный (минимаксный) критерий
x * arg max min qij .
i
j
Критерий минимаксного сожаления Сэвиджа
sij qij min qij , x * arg min max sij
i
i
j
Критерий пессимизма – оптимизма Гурвица
g( x i ) min qij (1 ) max qij , 0 1.
j
при
α=1
j
x * arg max g( x i )
i

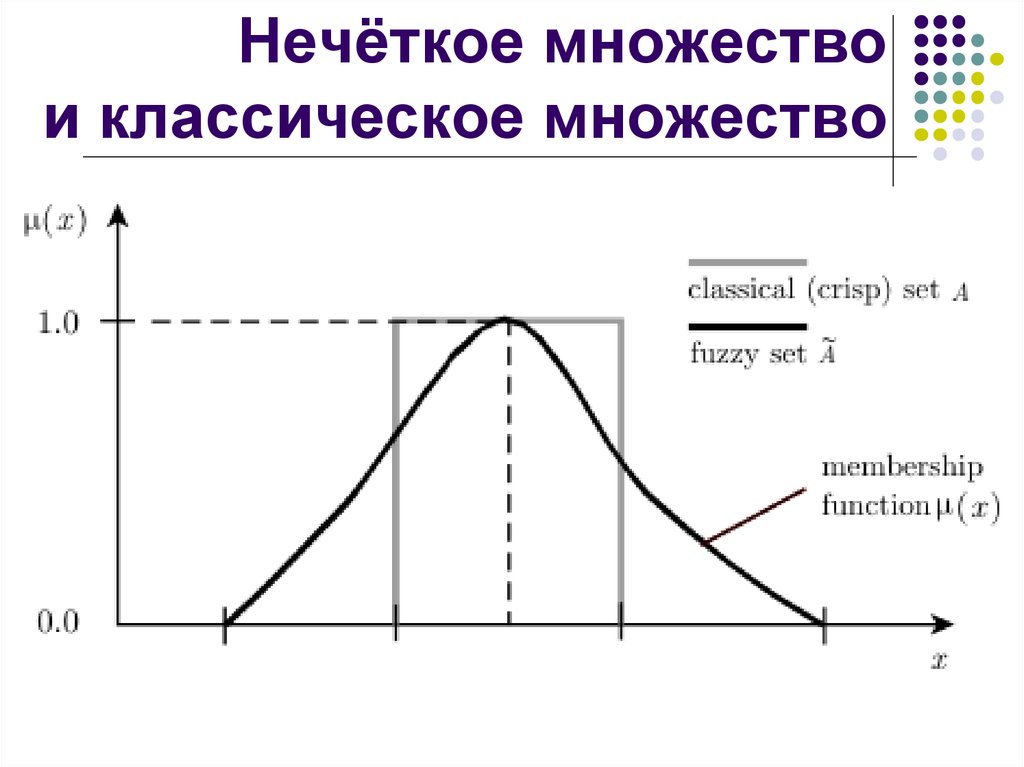
30. Нечёткое множество и классическое множество

31. Выбор на нечетком множестве альтернатив

x * arg max D ( x )
x X
μD(x) = min [μG(x), μC(x)] - нечеткое множество
решений D
G = {x, μG(x)} - нечеткое множество целей
C = {x, μC(x)} - нечеткое множество
ограничений
d( x i , x j )
1
( m
m
p
| r ( x i ) r ( x j )| )
1
μr(x) – функция принадлежности по r-му
признаку
1
p

32. Бинарные отношения на языке нечетких множеств

R ( x i , x k ) max{min[ R ( x i , x j ), R ( x j , x k )]}
xj
п ри ( x i , x j ) R ,
R (x i, x j )
0 п ри ( x i , x j ) R ,

33. Задачи выбора в системном анализе

34. Задачи выбора в системном анализе

35. Контрольные вопросы

1. В чем состоит метод свертки в задаче
многокритериальной оптимизации?
2. Какой смысл имеет множество
Парето?
3. Перечислите способы задания
отношений на конечном множестве.
4. Какие свойства имеет отношение
эквивалентности?

36. Тема. Методы выбора и принятия решений

1. Постановка задачи
многокритериальной
оптимизации.
2. Оптимизация методом свертки
частных критериев.
3. Оптимизация методом уступок.
4. Метод Парето-оптимизации
5. Способы задания отношений на
конечном множестве.

37. Тема. Методы выбора и принятия решений

6. Свойства отношений эквивалентности, порядка и доминирования.
7. Схема принятия статистических
решений.
8. Платежная матрица игровых
моделей.
9. Критерии выбора в условиях
неопределенности исходов.
10. Выбор на нечетком множестве
альтернатив.