Similar presentations:
Многокритериальные задачи принятия решения. Скаляризация
1. Многокритериальные задачи принятия решения. Скаляризация
2. Следует повторить
• Графический метод решения ЗЛП• Критерий
– Скалярный
– Векторный
– Позитивный
– Негативный
• Решение многокритериальной задачи
– Идеальное
– Компромиссное
• Векторная оценка альтернативы
• Множество векторных оценок
3. План лекции
1. Нормирование критериев
2. Метод аддитивной свертки критериев
3. Метод главного критерия
4. Лексикографическая оптимизация
5. Метод последовательных уступок
6. Метод целевого программирования
7. Принцип гарантированного результата (метод
максиминной свертки)
• 8. Метод равных наименьших относительных
отклонений
4.
а) Методы, использующие ограничения накритерии;
• метод ведущего критерия
• метод последовательных уступок.
б) Методы целевого программирования;
в) Методы, основанные на отыскании
компромиссного решения;
г) Методы, в основе которых лежат человекомашинные процедуры принятия решений
(интерактивное программирование).
5. Нормирование критериев
Нормирование – приведение критериев к единомумасштабу и безразмерному виду.
f1( x )
f ( x ) ... max
x X
f ( x )
m
g1( x )
g( x ) ... max
x X
g ( x )
m
gi ai fi bi
ai 0, bi
x, y X : x
fi x fi y
- некоторые константы
y
gi x g i y
Решение задачи не изменится при переходе от функций
fi к функциям gi
6.
Некоторые варианты нормированияПусть fk* – оптимальное, fk* – гарантированное значение критерия fk
Замена абсолютных значений критериев их:
1)безразмерными относительными величинами:
fk ( x )
fk ( x )
,
fk *
fk * max fk ( x ) 0
x X
2)относительными значениями отклонений
значений критериев f*k
fk ( x ) fk *
fk ( x )
3)относительными оценками:
gk x
fk *
от
оптимальных
,
fk x fk *
fk* fk *
Заметим, что gk(xk*) = 0, gk(xk*) = 1, для остальных x X gk(x) [0; 1].
7. Метод аддитивной свёртки
Пусть критерии соизмеримы (например, нормированы) иопределен вектор весовых коэффициентов критериев
=( 1,…, m), характеризующих важность соответствующего
критерия (если fi f j то i j ):
m
1, 0, i 1, m.
i
i 1
i
Решается задача оптимизации скалярного критерия:
m
F ( x ) i fi ( x ) max, x X
(4)
i 1
! Решение задачи (4) эффективно (т.е. Парето-оптимально) для исходной
многокритериальной задачи
8. Пример решения задачи методом аддитивной свёртки
Весовые коэффициенты:f ( x ) (f1 x1 3 x 2 , f2 40 x1 10 x 2 ) max
X 2 x1 x2 90, x1 x2 90, x2 50, x1, x 2 0
1 0,3, 2 0,7
Нормировка критериев
Находим f ,f
, решая задачу отдельно по каждому из критериев:
По второму критерию:
По первому критерию:
*
1
*
2
x1* = (10, 50), f1* = 160
x 2* = (45,0), f2* = 1800
Нормированные критерии
f1
f1
f
1
1
( x 1 3 x 2 ), f2 2*
(40 x 1 10 x 2 )
*
f1
160
f2
1800
Линейная свертка критериев:
F ( x ) 0,3f 1 0,7f 2 0,3
1
1
( x1 3 x 2 ) 0,7
(40 x 1 10 x 2 ) (25,1x 1 13,7 x 2 ) / 720
160
1800
9. Недостатки метода аддитивной свертки
1. Значения , как правило, устанавливаютсяисходя из неформальных соображений,
связанных с результатами экспертного анализа.
2. Вообще говоря априори не ясно, в каком
соотношении должны находиться весовые
коэффициенты, если известно желательное
отношение значений критериев на оптимальной
точке.
3. Возможны «плохие» значения некоторых
критериев за счет достаточно «хороших»
значений остальных целевых функций.
10. Метод главного критерия
• Один критерий выделяется в качестве главного• Остальные критерии переводятся в разряд ограничений.
Пусть – ( 2 , 3 ,..., m ) вектор, компоненты которого – это нижние
границы соответствующих критериев.
Решение считается оптимальным, если критерий f1 достигает своего
максимального значения при условии, что по всем остальным
критериям достигнуты значения, не меньше заданных.
Задача будет иметь вид:
F ( x ) f1( x ) max
fi ( x ) i , i 2, m,
x X.
Метод ведущего критерия применяется в таких задачах, как:
• минимизация полных затрат,
•максимизация выпуска комплектных наборов при ограничении на
потребляемые ресурсы
11. Пример
f ( x , y ) (f1 x , f2 y ) max,X {( x , y } | ( x 2)2 ( y 2)2 4, x 0, y 0}.
2 1
f1 x max
f2 y 1
(x, y ) X
x
a
c
0
1
b
y
Решение задачи – это точка c на рис. ,
множество эффективных точек
Э
X {a, b}, c X Э .
Проблемы принципа:
• Возможно наличие нескольких «главных» критериев, находящихся в
противоречии друг с другом.
• Не всегда ясен алгоритм выбора нижних границ
• Решение может быть слабоэффективно, но не эффективно
i
12. Лексикографические оптимумы.
1. Критерии нумеруются в порядке убывания их важности.f1
f2
...
fm
2. Определяется значение
.
f1* max f1( x ), X 1* argmax f1( x ), x X
x X
3. Решается задача:
f2 ( x ) max, x X 1*
Пункты 2 и 3 повторяются для критериев
f2,..., .fm
Недостаток метода:
уже на первом шаге множество может состоять из единственного
элемента и остальные функционалы не принимают никакого участия в
построении оптимального решения.
Этот недостаток исправляется следующим методом.
13. Метод последовательных уступок
1. Критерии нумеруются в порядке убывания их важности.f1 f2 ... fm
f1( x ) . ЛПР
2. Определяется значение f1* max
x X
устанавливает величину уступки Δ1 по этому критерию.
3. Решается задача:
f2 ( x ) max, x X , f1( x ) f1* 1.
Пункты 2 и 3 повторяются для критериев f2,..., f.m
Недостаток
Получаемое решение не всегда является эффективным.
14.
Пример 6. Решить задачу с уступкой по первому критерию 10% отего оптимального значения
f ( x ) (f1 x1 3 x 2 , f2 40 x1 10 x 2 ) max
X 2 x1 x2 90, x1 x2 90, x2 50, x1, x2 0
Решение. 1 этап.
Решим задачу по критерию
f1
f2
f1* 160 Величина уступки 1 16
*
Дополнительное ограничение: f1 ( x ) f1 1 x1 3x 2 160 16
2 этап: Решаем задачу
f1
Получим
f2 40 x1 10 x 2 max
2 x1 x 2 90x 3 x 160 16
1
2
x1 x 2 90
x 2 50
x1, x 2 0,
Ответ:
x * (18,42), f2 ( x * ) 1440, f1( x * ) 144
(A)
15.
Проблемы метода:- Произвольный выбор уступок может привести к
тому, что у задачи (А) не будет допустимых планов.
– решение задачи (А) может в общем случае не
быть оптимальным по Парето для задачи (исходной);
– числа i не соизмеряются между собой и обычно
подбираются по принципу: выберем достаточно
маленькие, если задача не будет иметь решения –
немного их увеличим.
16. Пример Решение задачи методом последовательных уступок
f1Пусть эксперты упорядочили критерии f2
Уступка по главному критерию составляет 3% от его
оптимального значения.
Задача 1-го этапа:
f ( x ) f2 40 x1 10 x 2 max
2 x 1 x 2 90
x1 x 2 60
x 2 50
x1, x 2 0,
Решение задачи первого этапа x 2* (10, 50), f2* 1800
Экспертом назначена уступка по главному критерию:
Δ2 = 0,03 * f2* = 0,03 * 1800 = 54
17.
Дополнительное ограничениеf2 ( x ) f2* 2
40 x1 10 x 2 1800 54 1746
Задача 2-го этапа:
f ( x ) f1 x1 3 x2 max
2 x1 x 2 90
x1 x 2 60
x 2 50
40 x1 10 x 2 1800 54 1746
x1, x 2 0,
Ответ: по методу уступок оптимальной является альтернатива
x * у (42,3; 5,4),
соответствующие значения критериев:
f1( x * у ) 58,5, f2 ( x * у ) 1746
Заметим, что
f1 ( x * у ) 58,5 160 f1* , f2 ( x * у ) 1746 1800 f2*
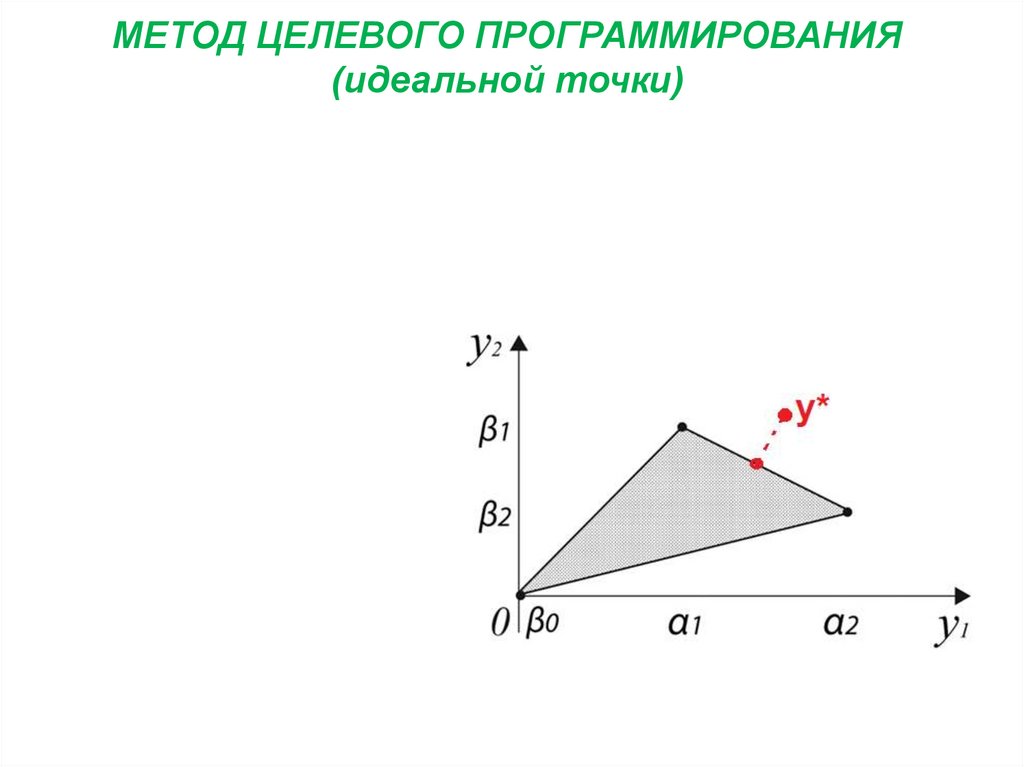
18. МЕТОД ЦЕЛЕВОГО ПРОГРАММИРОВАНИЯ (идеальной точки)
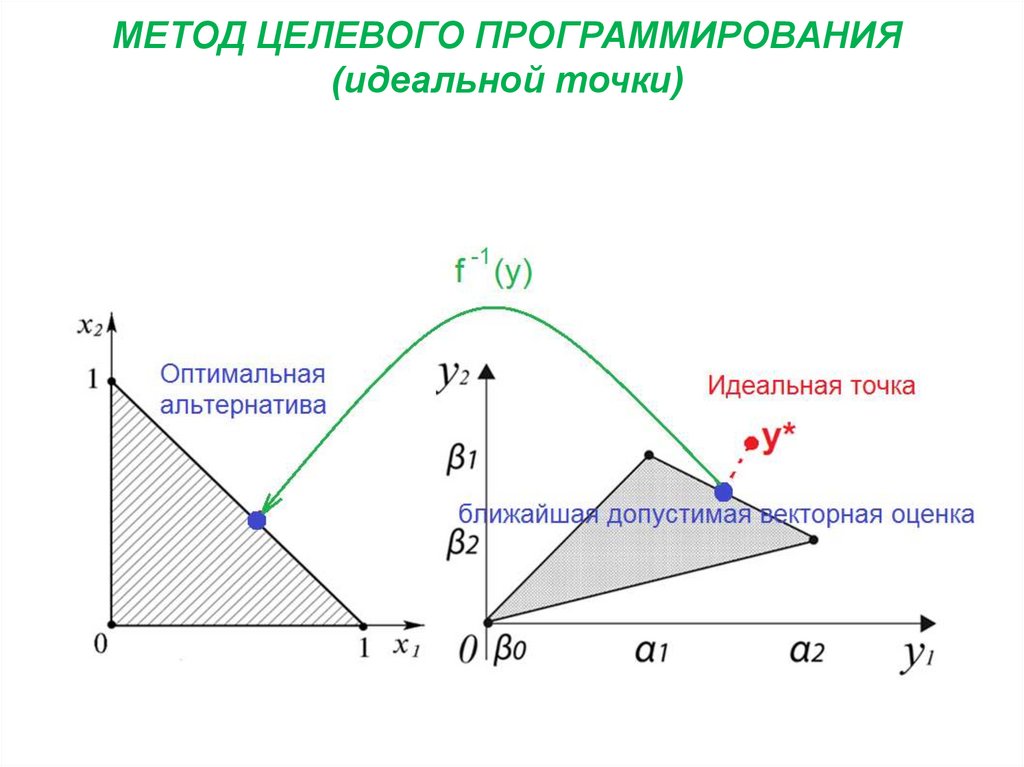
19. МЕТОД ЦЕЛЕВОГО ПРОГРАММИРОВАНИЯ (идеальной точки)
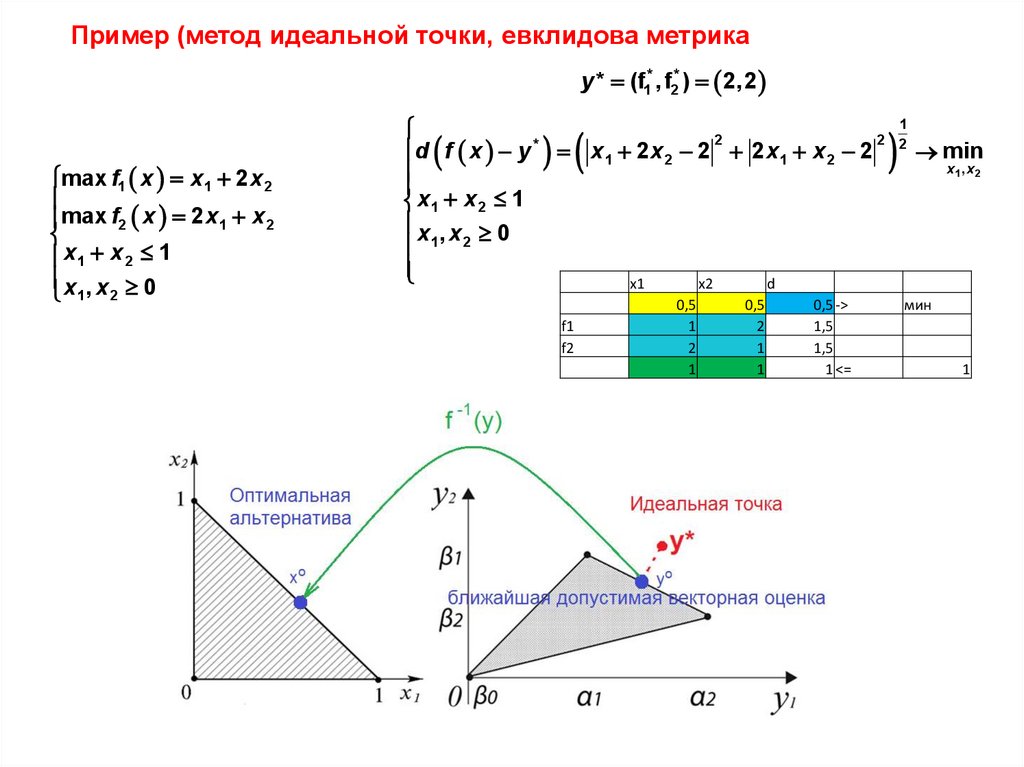
20.
Пример (метод идеальной точки, евклидова метрикаy * (f1* , f2* ) 2,2
max f1 x x1 2 x 2
max f2 x 2 x1 x 2
x1 x 2 1
x , x 0
1 2
1
2
2
d f x y * x1 2 x 2 2 2 x1 x 2 2 2 min
x1 , x 2
x1 x 2 1
x , x 0
1 2
x1
f1
f2
x2
0,5
1
2
1
d
0,5
2
1
1
0,5 ->
1,5
1,5
1 <=
мин
1
21.
МЕТОД ЦЕЛЕВОГО ПРОГРАММИРОВАНИЯ(идеальной точки)
* p
d(f(x),y ) = w i fi (x) - y i
i 1
n
1/p
*
min
x X
где y * y 1* ,..., y m* - вектор целевых значений,
*
.
d(f(x),y
) - расстояние (мера отклонения) между f(x)
и y * , 1 p , w i - весовые коэффициенты.
Часто (например, в случае линейного целевого
программирования) полагают p=1.
22. МЕТОД КОМПРОМИССНОГО РЕШЕНИЯ максиминной свертки
Принцип гарантированного результата. Задачаформулируется следующим образом:
fi ( x )
min * max, x X
i
fi
f (x )
fi
f (x )
fi
min i * i * 0
i
Эквивалентная задача:
max,
-задача:
fi ( x )
* 0,
fi
x X.
Получаемое решение эффективно. Оптимальное значение
max , 0 1
Чем меньше
тем противоречивее
критерии
23.
Примерf ( x ) (f1 8 x1, f2 10 x 2 ) max,
5 x1 3 x 2 450,
2 x1 6 x 2 420,
.
x1, x 2 0.
Решение. Находим решение по каждому из критериев:
f1* 720, x1* (90,0), f2 ( x1* ) 0,
f 700, x (0,70), f1 ( x ) 0,
*
2
*
2
*
2
max,
90 x1 0, 70 x 2 0,
x 1 , x 2 0,
5 x1 3 x 2 450, 2 x1 6 x 2 420.
Ответ
0,6818; x * 61,36; 47,73
f1 8 61,36 546,88, f2 10 47,73 477,3
f1 ( x ) 8 x 1
*
f1
720
f2 ( x ) 10 x 2
*
f2
700
x1 61,36; x 2 47,73
24. МЕТОД ИНТЕРАКТИВНОГО ПРОГРАММИРОВАНИЯ
• В методах основанных на человеко-машинныхпроцедурах (методы интерактивного
программирования) решение задачи происходит
в интерактивном режиме.
• ЛПР оценивает полученное решение и вносит или
изменяет заранее заданные коэффициенты или
уступки по критериям, а также определяет
направление оптимизации. Эта информация
служит для постановки новой задачи оптимизации
и получения промежуточного решения.
Диалог продолжается до тех пор, пока решение не
будет удовлетворять требованиям ЛПР.
25. Резюме
1. Нормирование критериев2. Метод аддитивной свертки критериев
3. Метод главного критерия
4. Лексикографическая оптимизация
5. Метод последовательных уступок
6. Метод целевого программирования
7. Принцип гарантированного результата (метод максиминной свертки)
8. Метод равных наименьших относительных отклонений



















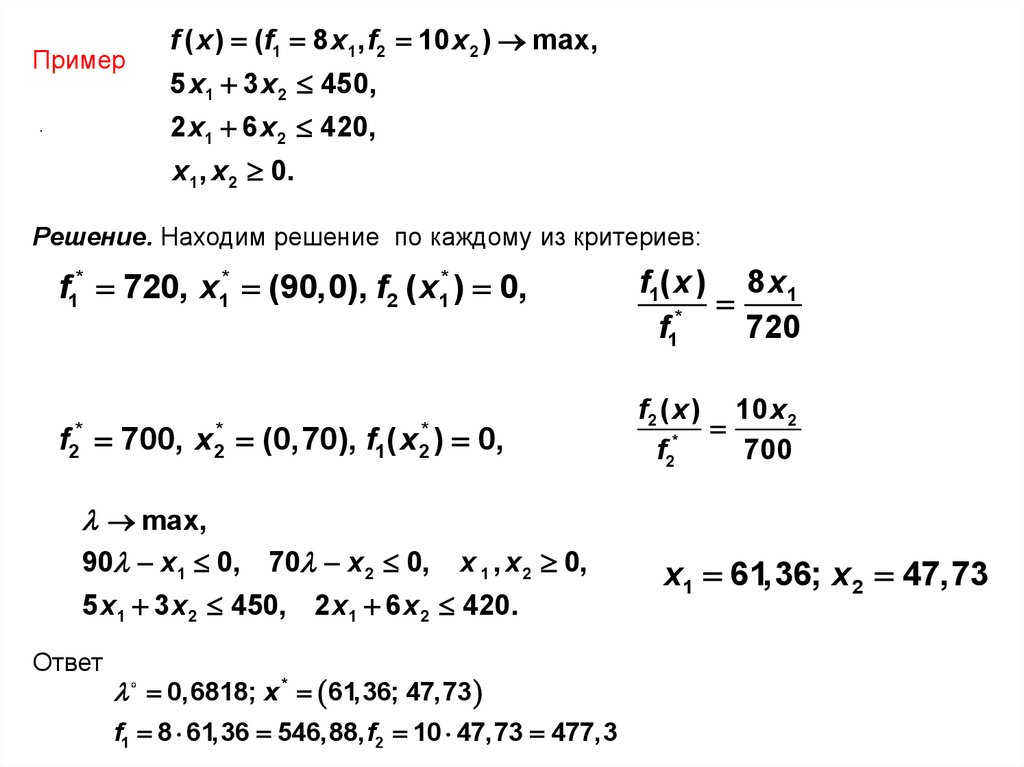


 mathematics
mathematics








