Методы принятия решений в условиях многокритериальности

1. 7. МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ МНОГОКРИТЕРИАЛЬНОСТИ

2.

Методы многокритериального анализа
Задачи развития ЭЭС являются многокритериальными, поэтому
поиск оптимального решения существенно затрудняется.
Успех оптимизации во многом зависит от сопоставимости
критериев.
Типы сопоставимости критериев
Количественный
Качественный
Несопоставимый
Методы сопоставления критериев
Метод
скаляризации
Метод
предпочтений
Метод
Парето

3.

Методы многокритериального анализа
Методn скаляризации
F a j Fj extr
j 1
Содержание – замена j = 1,..n
критериев одним скалярным.
Трудности – проблема определения весовых коэффициентов
aj .
Пример, в формуле приведенных затрат З Ен К И весовыми
коэффициентами являются Ен и 1. Случаи, когда критерии
выражаются в одинаковых единицах измерения, редки.
При выражении критериев в разных единицах измерения удобно
предварительно приводить их к безразмерному виду. Наиболее
часто используются:
- нормирование - выражение критериев в долях от некоторой
базисной величины
- центрирование - вычитание из значений критериев их средней
арифметической величины .

4.

Методы многокритериального анализа
Метод скаляризации
n
F a j Fj extr
j 1
Нормирование критериев
Fjнорм Fj Fj
m
F jцент
1
F j Fij ;
m i 1
F j ,F j max ,F j min
-
Нормированный
скалярный критерий
Центрирование критериев
Fj Fj
F j
F j F jmax F jmin
среднее, максимальное и минимальное
значения
(i =1,..) критерия
j,
m – число вариантов
n
F p j FjН extr
j 1
p j - весовые коэффициенты критериев
n
j 1
pj 1
4

5.

Методы многокритериального анализа
Метод предпочтений
При качественной сопоставимости критериев, когда невозможно
задать
весовые
коэффициенты
критериям,
но
можно
проранжировать их по степени убывания важности (обычно
ранжирование осуществляется экспертами).
Возможность
оптимизации
при
этом
обеспечивается
неопределенностью
информации,
являющейся
причиной
существования множества планов, не различающихся по
критерию оптимальности ( вероятно-оптимальных планов).
Неопределенность
информации
может
быть
объяснена
следующими причинами:
- неопределенностью прогноза внешних условий развития;
- погрешностью моделирования функционала цели;
погрешностью
модели,
возникающей
как
результат
агрегирования и приближенности моделирования связей;
- погрешностью метода решения;
- погрешностью реализации решения.

6.

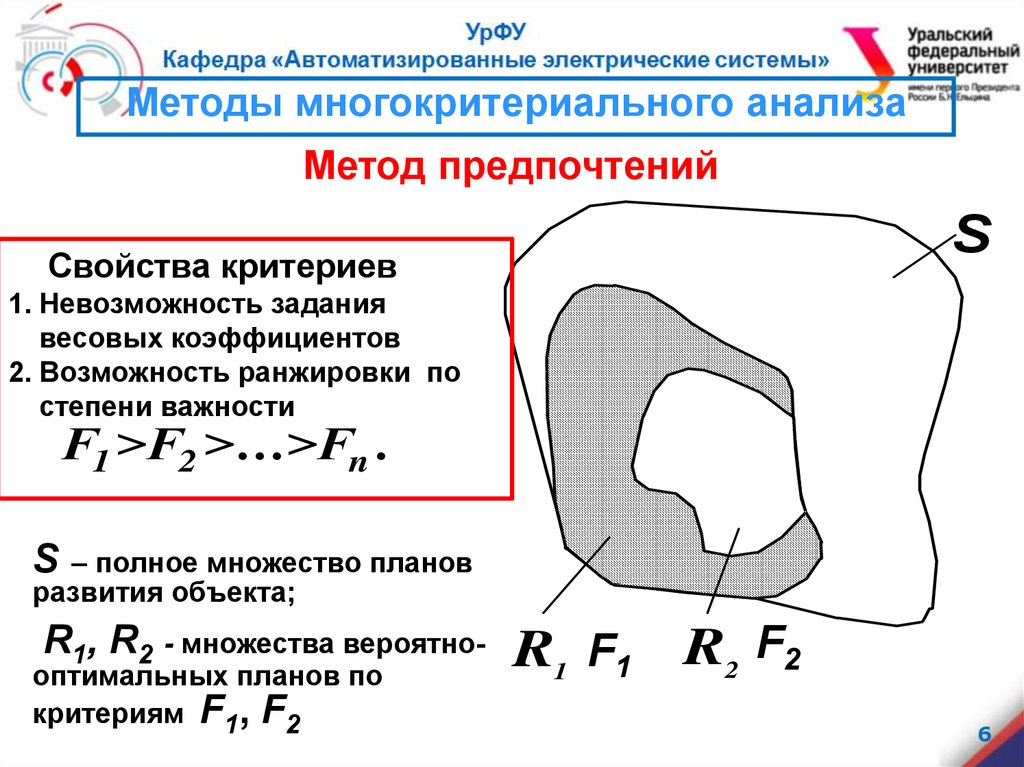
Методы многокритериального анализа
Метод предпочтений
S
Свойства критериев
1. Невозможность задания
весовых коэффициентов
2. Возможность ранжировки по
степени важности
F1 >F2 >…>Fn .
F
S
– полное множество планов
развития объекта;
R1, R2 - множества вероятно-
оптимальных планов по
критериям F1, F2
R1 F1 R2 F2
6

7.

Методы многокритериального анализа
Метод предпочтений
Алгоритм оптимизации по методу предпочтений
1. Формируется множество планов (вариантов развития) S ,
допустимых по всем критериям.
2. На множестве S осуществляется однокритериальная
оптимизация по наиболее важному критерию F1 и определяется
множество вероятно-оптимальных планов R1.
3. На множестве R1 выполняется оптимизация по следующему по
важности критерию F2 и определяется множество планов R2.
Процесс продолжается до рассмотрения последнего критерия или
до некоторого критерия Fj , множество вероятно-оптимальных
планов которого неразличимо по критерию Fj+1 .

8.

Методы многокритериального анализа
Метод Парето
Сложным
случаем
принятия
решения
в
условиях
многокритериальности является ситуация, когда критерии
несопоставимы
как
количественно,
так
и
качественно.
Основополагающим принципом сопоставления альтернатив при
этом является принцип Парето.
Принцип Парето - альтернативы (варианты) считаются
неразличимыми по оптимальности, если ни одну из них нельзя
улучшить ни по одному из критериев, не ухудшив хотя бы по
одному из остальных.
Множество
вероятно-оптимальных
альтернатив,
удовлетворяющих принципу Парето, является множеством Парето
(множеством компромиссов).
8

9.

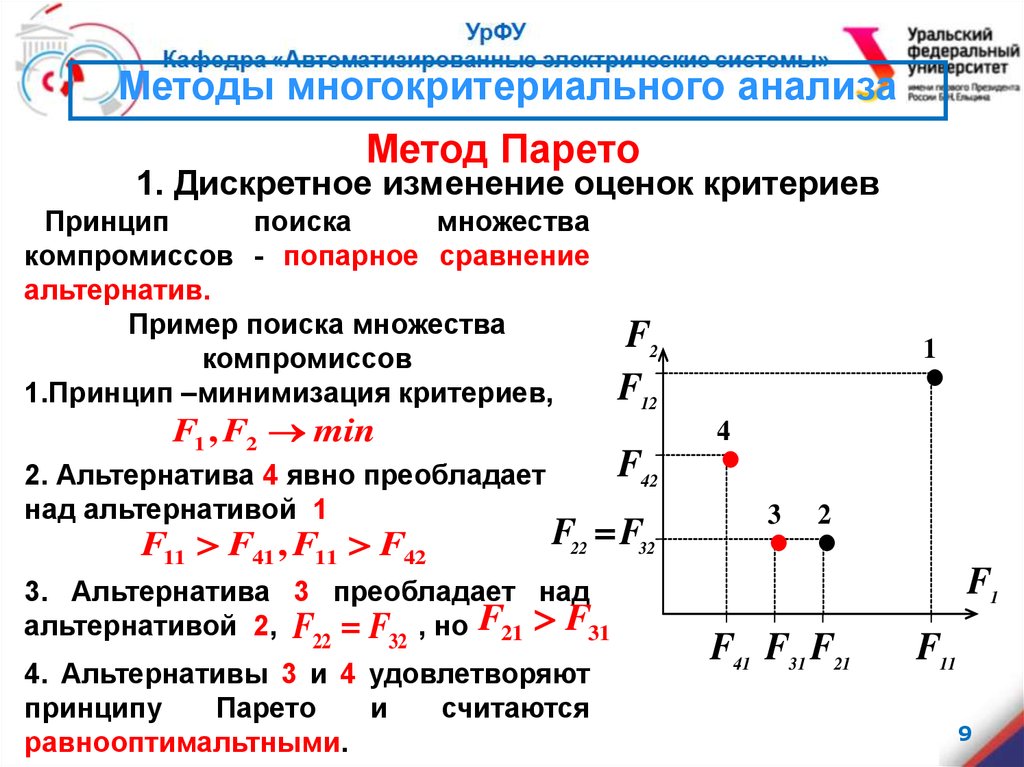
Методы многокритериального анализа
Метод Парето
1. Дискретное изменение оценок критериев
Принцип
поиска
множества
компромиссов - попарное сравнение
альтернатив.
Пример поиска множества
компромиссов
1.Принцип –минимизация критериев,
F1 , F2 min
2. Альтернатива 4 явно преобладает
над альтернативой 1
F11 F41 , F11 F42
F2
F12
1
4
F42
F22 F32
3. Альтернатива 3 преобладает над
альтернативой 2, F22 F32 , но F21 F31
4. Альтернативы 3 и 4 удовлетворяют
принципу
Парето
и
считаются
равнооптимальтными.
3
2
F1
F41 F31 F21
F11
9

10.

Методы многокритериального анализа
Метод Парето
Особенности использования метода Парето в
условиях неопределенности
Наиболее сложным случаем принятия решения в условиях
многокритериальности является ситуация, когда критерии
изменяются не дискретно, а непрерывно и несопоставимы
количественно. При этом возникает бесконечное множество
альтернатив.
Оценки по критериям изменяются непрерывно
непрерывном изменении параметров управления.
при
Попарное сравнение альтернатив невозможно.
10

11.

Методы многокритериального анализа
Метод Парето
2. Непрерывное изменение оценок критериев
F2
А3
Множество допустимых
альтернатив непрерывно и
ограничено
замкнутой
кривой.
Любую
альтернативу
(А1),
принадлежащую
множеству,
можно
улучшать,
двигаясь
в
направлении
вектора,
лежащего
в
третьем
квадранте,
улучшение
альтернативы
будет
продолжаться
до
достижения
границы
множества (А2).
А1
А4
Fa2
Fb2
a
b
Fc2
А2
c
Fd2
d
Fa1 Fb1
Fc1
Fd1
F1
11

12.

Методы многокритериального анализа
Метод Парето
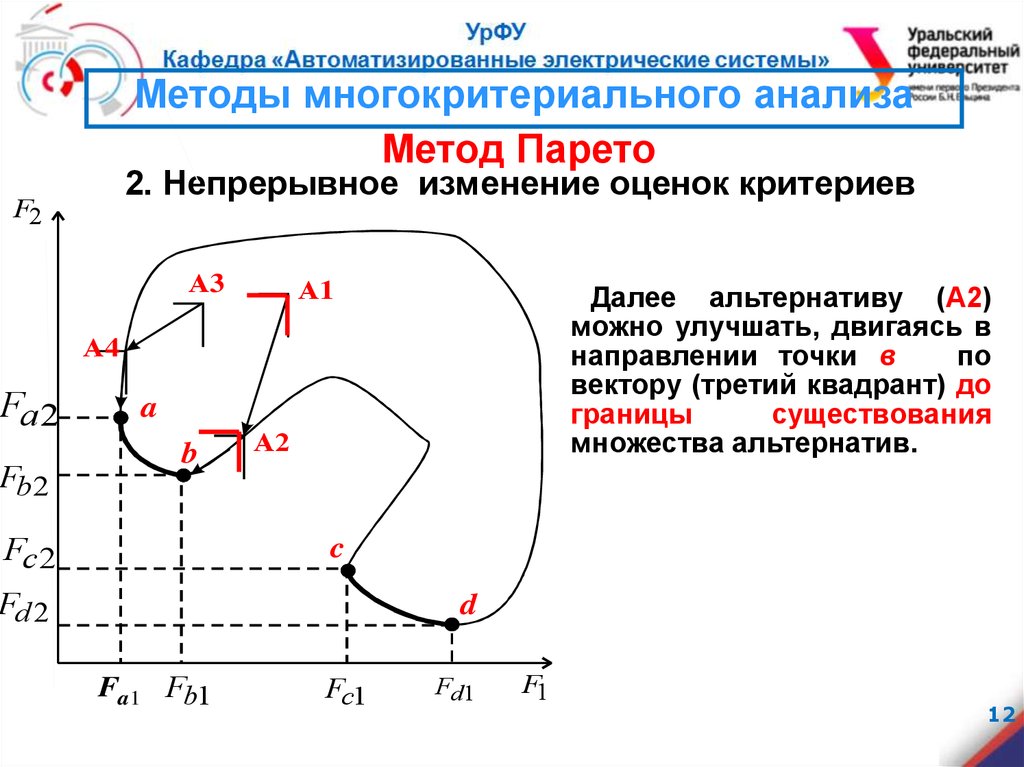
2. Непрерывное изменение оценок критериев
F2
А3
А1
Далее альтернативу (А2)
можно улучшать, двигаясь в
направлении точки в
по
вектору (третий квадрант) до
границы
существования
множества альтернатив.
А4
Fa2
Fb2
a
b
Fc2
А2
c
Fd2
d
Fa1 Fb1
Fc1
Fd1
F1
12

13.

Методы многокритериального анализа
Метод Парето
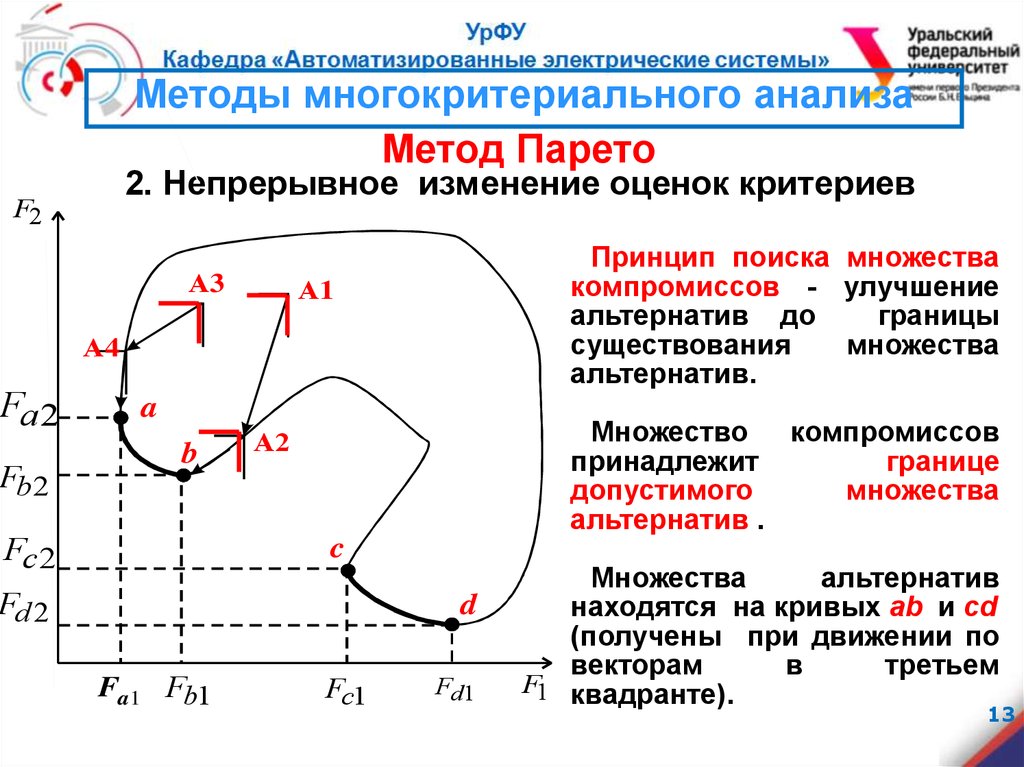
2. Непрерывное изменение оценок критериев
F2
А3
Принцип поиска множества
компромиссов - улучшение
альтернатив до
границы
существования
множества
альтернатив.
А1
А4
Fa2
Fb2
a
b
Fc2
Множество компромиссов
принадлежит
границе
допустимого
множества
альтернатив .
А2
c
Fd2
d
Fa1 Fb1
Fc1
Fd1
Множества
альтернатив
находятся на кривых ab и cd
(получены при движении по
векторам
в
третьем
F1 квадранте).
13

14.

Методы многокритериального анализа
Анализ множества Парето
1. Альтернативы, образующие множество Парето, теоретически
равнооптимальны. Часто количество альтернатив в множестве
компромиссов оказывается слишком большим, требуется о его
сократить ибо лицо принимающее решение должно сделать
единственный выбор.
2.
Практически существуют возможности сопоставления и
дальнейшего отсеивания менее рациональных альтернатив.
3. Анализ альтернатив внутри множества компромиссов
вторжение во множество компромиссов.
-
4. Один из методов - районирование решений (альтернатив) в
пространстве критериев.
14

15.

Методы многокритериального анализа
Районирование альтернатив в пространстве критериев
Две альтернативы
при трех критериях
B1 и B 2 удовлетворяют принципу Парето,
F1 , F2 ,F3 .
Алгоритм районирования альтернатив
1. Образование скалярного
весовыми коэффициентами
критерия
F
с неизвестными
pi
F p1F1 p2 F2 p3 F3 , p1 p2 p3 1.
F p1F1 p2 F2 1 p1 p2 F3
15

16.

Методы многокритериального анализа
Районирование альтернатив в пространстве критериев
3. Определение критических значений весовых коэффициентов
p1к , p2к при которых альтернативы B1 и B 2 по скалярному
F критерию строго равнооптимальны.
Если
, тогда
FB1 FB2
p1к F11 p2к F12 1 p1к p2к F13
p1к F21 p2к F22 1 p1к p2к F23 .
Это уравнение прямой в осях p1 и
имеют одинаковые оценки вариантов
критерию,
FB1 FB2
p2 . Все точки на прямой
B1 и B 2 по скалярному
16

17.

Методы многокритериального анализа
Районирование альтернатив в пространстве критериев
p1к F11 p2к F12 1 p1к p2к F13
p1к F21 p2к F22 1 p1к p2к F23 .
После преобразования
уравнение прямой
имеет вид
p1к F11 F13 F21 F23 p2к F12 F13 F22 F23
F23 F13
17

18.

Методы многокритериального анализа
Районирование альтернатив в пространстве критериев
Множество возможных сочетаний весовых коэффициентов
ограничено прямоугольным треугольником в осях p1 и p2 ,
ограниченным координатными осями и отрезком с координатами
(1,0) и (0,1).
Для определения зон эффективности следует сравнить
значения скалярного критерия F для альтернатив B1 и B 2 .
Пусть зона эффективности варианта B1 определяется
множеством
весовых
коэффициентов,
ограниченным
многоугольником bcde.
Тогда
зона
эффективности
варианта B 2 определяется
треугольником abc.
Если зона эффективности варианта B1 больше зоны
эффективности варианта
B 2 , то вариант B1 более
предпочтителен.
18

19.

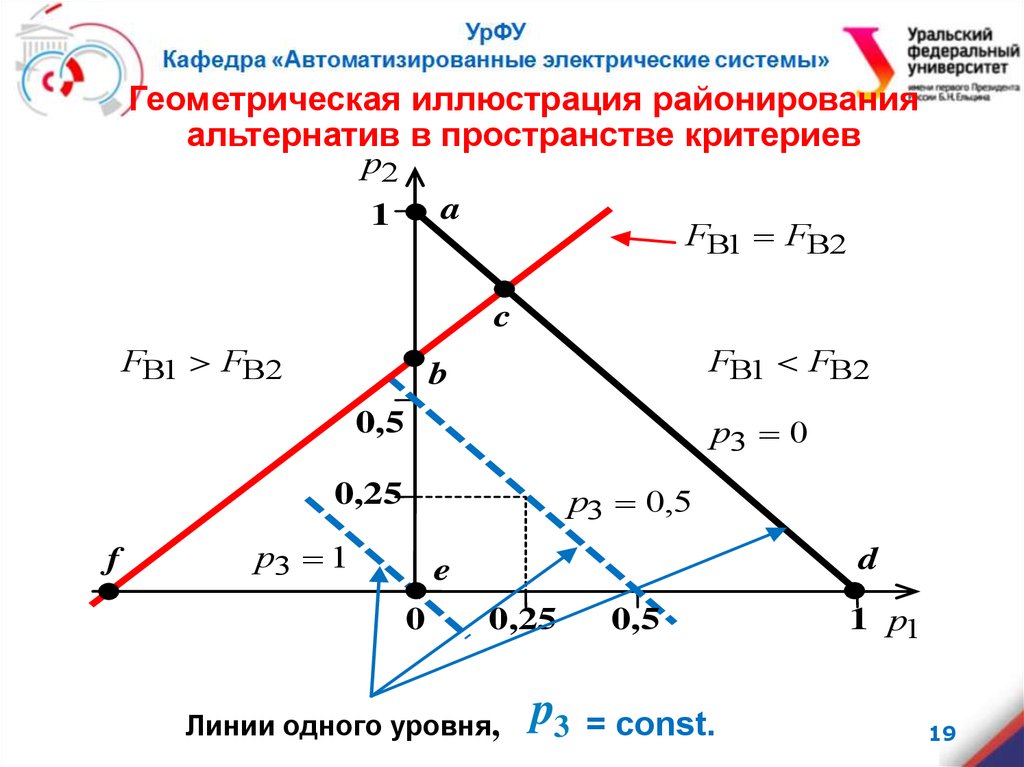
Геометрическая иллюстрация районирования
альтернатив в пространстве критериев
p2
a
1
FB1 FB2
c
FB1 FB2
FB1 FB2
b
0,5
p3 0
p3 0,5
0,25
f
p3 1
d
e
0
0,25
Линии одного уровня,
p3
0,5
= const.
1 p1
19

20.

Методы многокритериального анализа
Этапы многокритериального анализа
1.
Агрегирование
информации
распознавания образов.
-
методы
таксономии
и
2. Поиск компромиссных решений при согласовании интересов
субъектов СУ - методы ситуационного анализа.
3. Анализ влияния факторов риска на принимаемые решения
(финансовые и экологические риски).
4. Исследование устойчивости решений к изменению расчетных
условий.
5. Нахождение областей эффективности альтернатив.
20

21.

МЕТОД ПАРЕТО
Районирование альтернатив в пространстве критериев
Задача. Четыре варианта сооружения электростанции
характеризуются
различными
показателями
по
трем
несопоставим критериям.
Дать рекомендации по предпочтительности вариантов.
Значения критериальных оценок по вариантам
№
п/п
1
2
3
Наименование критерия
Ед.
изм.
Варианты
1
2
3
4
Расчетные ежегодные выбросы
загрязняющих веществ
тыс.
тонн
154
206
138
215
Ежегодные приведенные затраты
по сооружению и эксплуатации
млн.
руб.
Среднегодовое ожидаемое
количество аварийных ситуаций
Случаев
1230 1200 1400 1400
3,0
4,2
3,5
4,3
21

22.

МЕТОД ПАРЕТО
Районирование альтернатив в пространстве критериев
Решение задачи.
1. Проверка образования вариантами множества компромиссов.
Анализ значений критериальных оценок вариантов:
- по первому критерию лучшим является вариант 3;
- по второму критерию - вариант 2;
- по третьему - вариант 1.
- вариант 4 явно уступает вариантам 1 и 2 по всем критериям и
варианту 3 по критериям 1 и 2, следовательно он не входит в
область Парето и не рассматривается.
Вывод - три варианта 1, 2 и 3 образуют множество Парето
(множество компромиссов), так как ни один из них нельзя
объявить худшим.
22

23.

МЕТОД ПАРЕТО
Районирование альтернатив в пространстве критериев
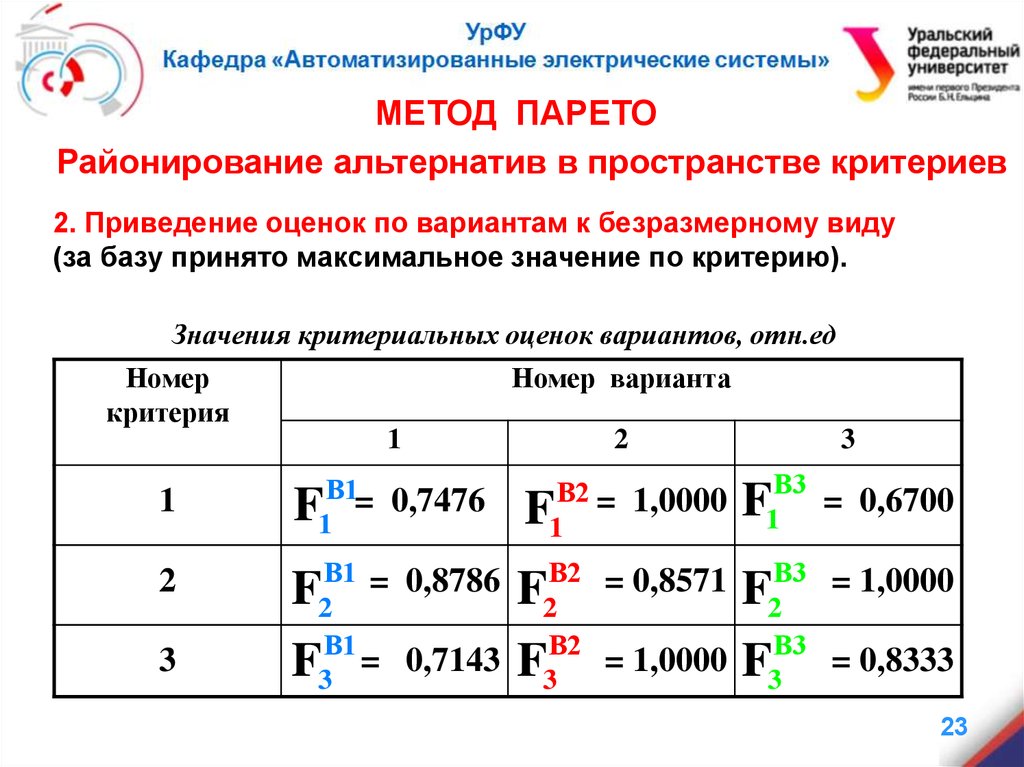
2. Приведение оценок по вариантам к безразмерному виду
(за базу принято максимальное значение по критерию).
Значения критериальных оценок вариантов, отн.ед
Номер
Номер варианта
критерия
1
2
3
1
2
3
В1=
1
F
В1 =
2
В1
=
3
F
F
0,7476
0,8786
0,7143
В2 =
1
F
В2
2
В2
3
F
F
1,0000
= 0,8571
В3
1
F
В3
2
В3
3
F
= 1,0000 F
= 0,6700
= 1,0000
= 0,8333
23

24.

(
3. Определение областей эффективности вариантов.
Сущность - получение уравнений прямых, разделяющих области
эффективности вариантов в пространстве критериев при
попарном сравнении вариантов.
p2
Область допустимых значений
весовых
коэффициентов
прямоугольный
треугольник
с
вершинами:
1
p1
0
1
( р1 1, р2 0, р3 0);
( р1 1, р2 0, р3 0);
( р1 0, р2 0, р3 1).
24

25.

3.1. Равенство оценок для пары вариантов 1 и 2
FВ1 = FВ2
р1 и
значения р1К и
можно записать через весовые коэффициенты первого
второго
р 2К
р2
критериев, придав им критические
при которых эффективности вариантов одинаковы.
Так как
р 3 =1-р1 -р 2 , то
условие
FВ1 = FВ2 имеет вид
р1К F1В1 +р2К F2В1 +(1-р1К -р2К )F3В1 = р1КF1В2 +р 2КF2В2 +(1-р1К -р 2К )F3В2
или
после
преобразования
р1К (F1В1 -F3В1 -F1В2 +F3В2 )+р 2К (F2В1 -F3В1 -F2В2 +F3В2 ) = F3В2 -F3В1
25

26.

,.
;
,
При подстановке числовых значений
по критериям уравнение
.
прямой, разделяющей области эффективности
вариантов 1 и 2 в
пространстве критериев имеет вид,
р1К (0,7476 - 0,7143 - 1,0 + 1,0) +
+р 2К (0,8786 - 0,7143 - 0,8571 + 1,0) = 1,0 - 0,7143
0,0333 р1К + 0,3072 р 2К = 0,2857
Две точки для построения прямой (В1=В2):
( р1К =
0, р 2К =0,93);
( р 2К = 0, р1К = 8,58 ).
Прямая (В1=В2) строится в осях весовых коэффициентов.
26

27.

Определение областей эффективности вариантов
FВ1 = FВ2
p2
1
0,93
В1
0
В2
Для
определения
областей
эффективности вариантов 1 и 2
необходимо сравнить варианты в
одной из точек любой из областей.
р = р 3 = 0, р 2 =1
В1 = В2 В красной точке 1
варианты можно сравнивать по
одному критерию F2 .
В1
В2
0,8786 = F2 < F2 = 0,8571.
В этой точке вариант 2 лучше
варианта
1
по
принципу
p1минимизации критериев.
Все точки красного треугольника,
1
выше прямой (В1=В2), принадлежат
области эффективности варианта 2.

28.

3.2. Равенство оценок для пары вариантов 1 и 3
В1
1К 1
В1
2К 2
В1
3
В3
1К 1
FВ1 = FВ3
В3
2К 2
В3
3
р F +р F +(1-р1К -р2К )F = р F +р F +(1-р1К -р 2К )F
.
В1
1
В1
3
В2
1
В2
3
В1
2
В1
3
В2
2
В2
3
В2
3
В1
3
р1К (F -F -F +F )+р 2К (F -F -F +F ) = F -F
0,1966 р1К - 0,0024 р 2К = 0,119 .
Две точки для построения прямой (В1=В3):
(р1к = 0, р 2к = -49,6); (р 2к = 0, р1к = 0,605) .
28

29.

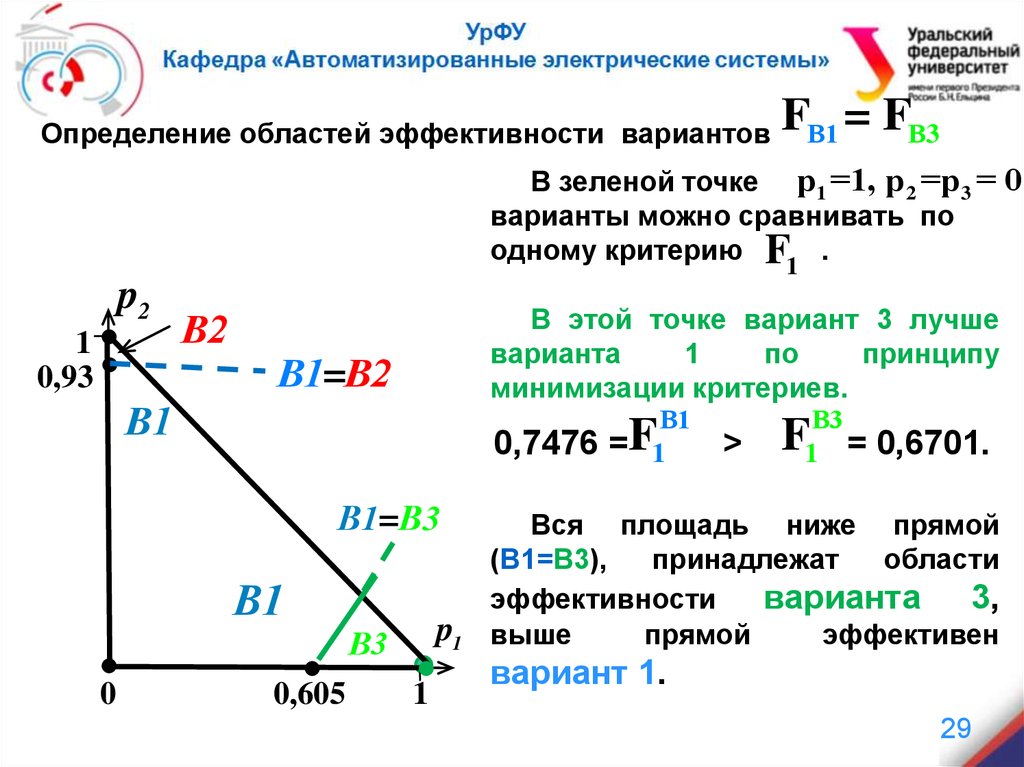
Определение областей эффективности вариантов
FВ1 = FВ3
В зеленой точке р1 =1, р 2 =р 3 = 0
варианты можно сравнивать по
одному критерию F1 .
p2
1
0,93
В2
В этой точке вариант 3 лучше
варианта
1
по
принципу
минимизации критериев.
В1=В2
В1
В1
1
0,7476 =F
В1=В3
В1
p1
В3
0
0,605
1
>
В3
1 =
F
0,6701.
Вся площадь ниже прямой
(В1=В3),
принадлежат
области
эффективности
варианта 3,
выше
прямой
эффективен
вариант 1.
29

30.

FВ2 =FВ3
3.3. Равенство оценок для пары вариантов 2 и 3
В2
1К 1
В2
2
В2
3
р F +р 2К F +(1-р1К -р 2К )F
р F +р 2К F +(1-р1К -р 2К )F
В3
1К 1
В3
2
В3
3
.
0,1633 р1К - 0,3096 р 2К = -0,1667 .
Две точки для построения прямой (В2=В3):
(р1К = 0, р 2К = 0,538); (р 2К = 0, р1К = -1,1875) .
30

31.

(
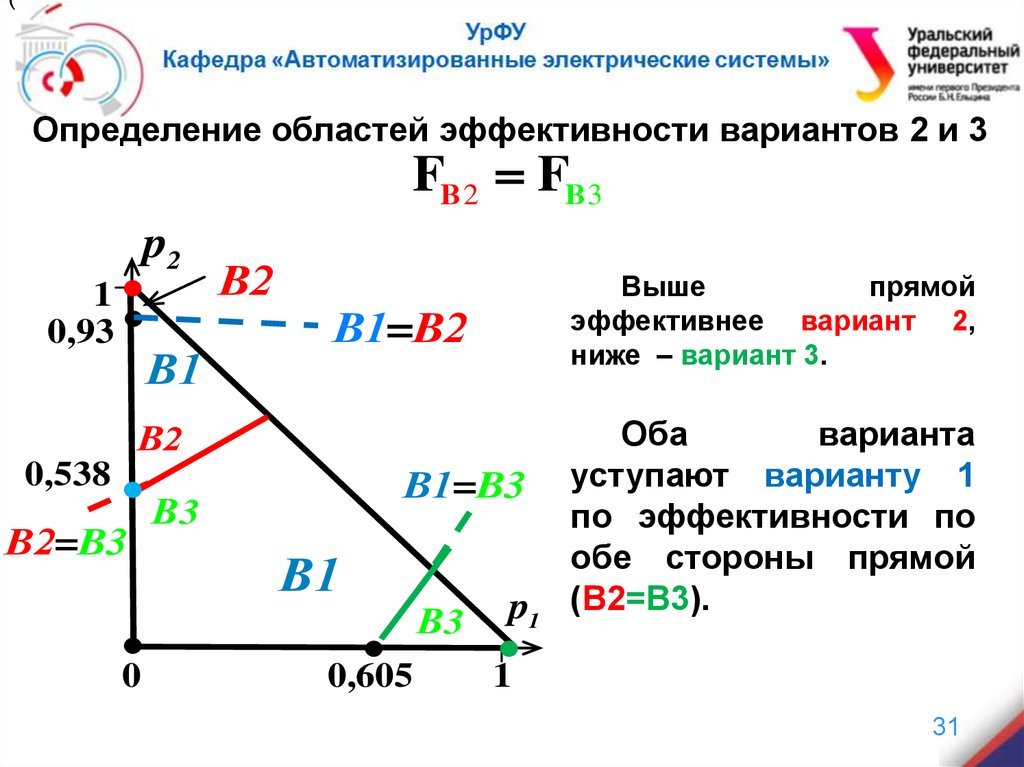
Определение областей эффективности вариантов 2 и 3
FВ 2 FВ 3
p2
1
0,93
В1
В2
Выше
прямой
эффективнее вариант 2,
ниже – вариант 3.
В1=В2
В2
0,538
В2=В3
В1=В3
В3
В1
В3
0
0,605
p1
Оба
варианта
уступают варианту 1
по эффективности по
обе стороны прямой
(В2=В3).
1
31

32.

Методы многокритериального анализа
Выводы по задаче
1. Область эффективности варианта 2 - маленький
треугольник выше отрезка (В1=В2).
2. Область эффективности варианта 3 - треугольник
правее отрезка (В1=В3).
3. На всей остальной области прямоугольного
треугольника
допустимых
значений
весовых
коэффициентов вариант 1 абсолютно доминирует над
вариантами 2 и 3.
4. Выполненные процедуры позволили провести
районирование области эффективности вариантов в
пространстве критериев.
Скорее всего, стоит отдать предпочтение варианту 1.
32

33. Обзор методов многокритериального анализа

ОБЗОР МЕТОДОВ
МНОГОКРИТЕРИАЛЬНОГО
АНАЛИЗА
33

34.

Методы многокритериального анализа
В современном понимании системы энергетики являются
открытыми человеко-машинными системами, предназначенными
для получения, преобразования, транспортирования, хранения и
распределения энергоресурсов и энергоносителей. Такие
системы
представляют
собой
взаимосвязанные
части:
топливоснабжающие, теплоснабжающие и электроснабжающие.
В настоящее время системы энергетики характеризуются
увеличением неопределенности условий функционирования и
целей развития.
В рыночных условиях социально-экономического развития
возникла ограниченность методов системных исследований в
энергетике, которые были развиты и ориентированы на
централизованное
управление
отраслями
хозяйства
и
предсказуемое развитие экономики.
34

35.

Методы многокритериального анализа
С ростом экономической самостоятельности субъектов РФ и
формированием рыночных отношений в значительной мере
расширился круг субъектов системы управления энергетикой.
Отмеченные
обстоятельства
требуют
соответствующего
развития средств и процедур обоснования и принятия решений
по структурной и технической политике в энергетике на основе
многокритериального анализа возможных альтернатив и
достижения
эффективного
компромисса
между
заинтересованными сторонами.
35

36.

Методы многокритериального анализа
Системы энергетики обладают такими свойствами больших
систем, как иерархичность решений, неполнота информации,
многокритериальность и инерционность.
На основе этих свойств задачи развития и оценки состояния
можно сформулировать как многокритериальный анализ
альтернатив
и
классификацию
состояний
в
условиях
неопределенности. Для решения таких задач перспективно
применение понятий и методов теории нечетких множеств.
Решение
задач
анализа
состояния
и
развития
электроэнергетических систем и их объектов осложняется
неопределенностью исходной информации при описании
текущего и перспективного состояния исследуемых объектов,
неопределенностью
критериев
качества
состояния
и
принимаемых
решений
по
рациональному
развитию
электроэнергетических систем.
36

37.

Методы многокритериального анализа
Адекватное
реальности
представление
энергосистемы
практически всегда содержит неопределенности различного типа.
Различают следующие типы неопределенностей:
- неопределенность целей;
- неопределенность природы;
- неопределенность действий противника или партнера.
Неопределенность целей в энергетике может быть
связана:
- с ее нечеткой формулировкой, обусловленной трудностью или
невозможностью четкого описания;
- с многозначностью целей, многоцелевой ситуацией.
37

38.

Методы многокритериального анализа
Например,
цель
«обеспечение
нормального
уровня
энергетической безопасности» является двояко неопределенной.
С
одной
стороны
понятие
нормальности
является
неопределенным, зависящим от конкретной территории и от
сформированных представлений.
С другой стороны, энергетическая безопасность включает в
себя
состояние
топливоснабжения,
теплоснабжения,
электроснабжения, финансовую состоятельность объектов
энергетики – электрических станций и электрических сетей, а
также множество других факторов неэнергетического характера,
прямо или косвенно влияющих на состояние защищенности
энергетических интересов граждан и государства.
38

39.

Методы многокритериального анализа
Неопределенность природы отражает степень нашего
незнания изучаемого объекта и его окружения, а также
невозможность определенного знания на прогнозный период.
Оценка текущего состояния ЭЭС связанна с неточностью
измерений, статистическим характером информации.
Для задачи развития часть информации, описывающей систему,
носит прогнозный, а, следовательно, объективно неопределенный
характер.
39

40.

Методы многокритериального анализа
Неопределенность
противника – это
действий
партнера
неопределенности внешней,
отношению к рассматриваемой системе, среды.
или
по
Например, уровень потребления электроэнергии, топлива,
тепла в расчетный год может быть указан как некоторый
интервал. Прогнозные возможности сопряженных отраслей
экономики, также несут в себе неопределенность.
40

41.

Методы многокритериального анализа
Когда
лицо,
принимающее
решение,
сталкивается
с
неопределенностью реальной системы в процессе принятия
решений, то он поступает самыми различными способами.
1.Сознательно или бессознательно игнорирует существование
неопределенности и использует детерминированные модели,
внося определенность в ситуации, где ее в действительности нет.
2. Выбирает один наиболее существенный, с его точки зрения, вид
неопределенности и использует соответствующую теорию, так как
разработанные в настоящее время количественные методы
принятия решений помогают выбрать наилучшие из множества
возможных решений лишь в условиях конкретного вида
неопределенности.
41

42.

Методы многокритериального анализа
Когда
лицо,
принимающее
решение,
сталкивается
с
неопределенностью реальной системы в процессе принятия
решений, то он поступает самыми различными способами.
3. Проводит дополнительные исследования системы
получает информацию в ходе контроля или управления.
или
4. Чаще всего, при невозможности использования других
методов учета неопределенности, проводит вариантные расчеты с
целью определения наилучшей стратегии управления по какомулибо компромиссному критерию.
42

43. СПАСИБО ЗА ВНИМАНИЕ !