Lektsia_2_1_Proizvodnaya_i_ee_primenenia (2)

1.

2.

Определение.
Производной функции y=f(x), заданной на
некотором интервале (a;b), в точке х этого
интервала,
называют
предел
отношения
приращения функции в этой точке к
соответствующему приращению аргумента, когда
приращение аргумента стремится к нулю.
Производную функции f(x) обозначают f '(x).

3. Алгоритм нахождения производной (для функции y=f(x)).

Зафиксировать значение х, найти f(x).
Дать аргументу х приращение ∆х, перейти в
новую точку х+∆х, найти f(x+∆x).
Найти приращение функции: ∆у=f(x+∆x)–f(x).
у
Составим отношения
.
x
Вычислить
Этот предел и есть f '(x).

4. Пример. Найти производную функции у=2х+3 в точке х=3

у (3) 2 3 3 9
f ( x x) 2 (3 x) 3 2 x 9
y y (3 x) y (3) 2 x
y 2 x
2
x x
f
2
lim
x x
у (3) = 2

5. Физический смысл производной

Если при прямолинейном движении путь s,
пройденной точкой, есть функция от времени t,
т.е. s=f(t), то скорость точки есть производная от
пути по времени, т.е. v(t)=f '(t), этот факт выражает
механический смысл производной.

6. Пример

Тело движется по прямой так, что расстояние S (в метрах) от
него до точки В этой прямой изменяется по закону
S (t ) 2t 3 12t 2 3(t – время движения в секундах). Через сколько
секунд после начала движения ускорение тела будет равно 36
м/ с 2?
Решение.
Из механического смысла производной имеем скорость – это
производная пути по времени. Скорость изменяется по закону
v(t ) S (t ) 6t 2 24t
Так как ускорение – это производная скорости по времени, то
ускорение изменяется по закону
a(t ) v (t ) 12t 24 , с другой стороны
ускорение равно 36 м/с 2 . Решим уравнение12t 24 36 , t=5 c.
Ответ: через 5 секунд.

7. Геометрический смысл производной

Если в точке х 0 к графику функции y=f(x) проведена
касательная, то число f '( х0 ) есть тангенс угла альфа
между
этой
касательной
и
положительным
направлением оси ОХ, т.е. f '( х 0 )=tgα. Этот угол
называю углом наклона касательной. Этот факт
выражает геометрический смысл производной.
Формулами дифференцирования называют формулы
для нахождения производных конкретных функций.

8. Пример

На рисунке изображен график функции y=f(x) и
касательная к нему в точке с абсциссой х . Найдите
значение производной функции f(x) в точке х 0.
0
Рис.1

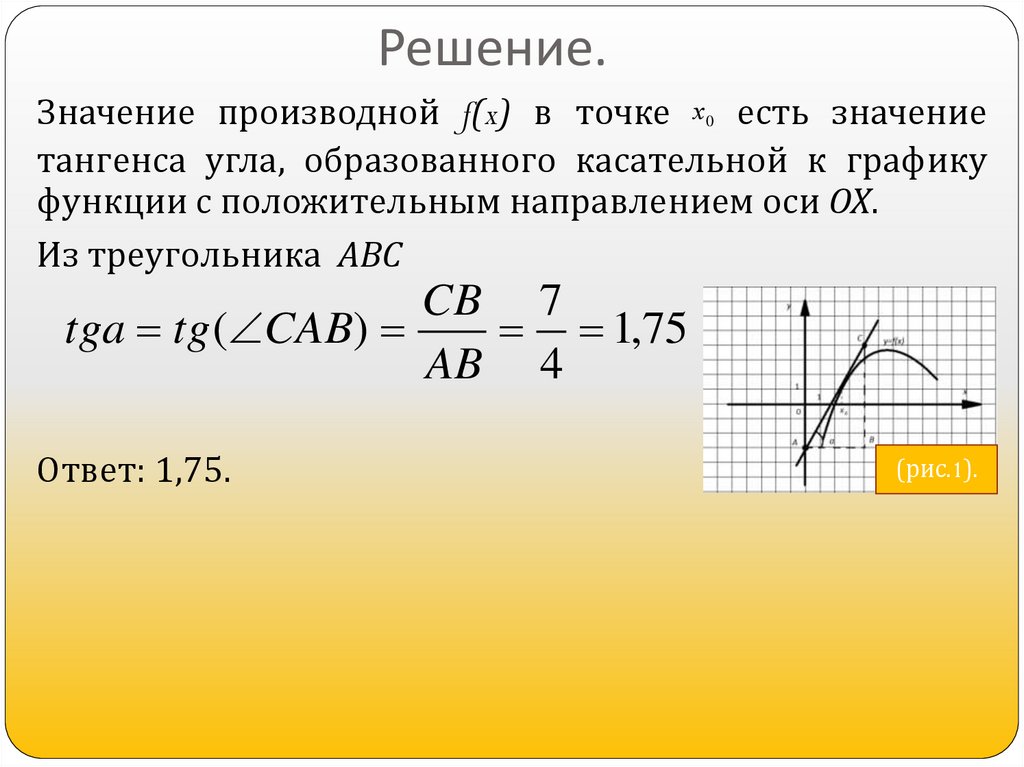
9. Решение.

Значение производной f(x) в точке х 0 есть значение
тангенса угла, образованного касательной к графику
функции с положительным направлением оси ОХ.
Из треугольника АВС
CB 7
tga tg ( CAB)
1,75
AB 4
Ответ: 1,75.
(рис.1).

10. Правила дифференцирования

Теорема 1.
Если функции y=f(x) и y=g(x) имеют производную в
точке x, то и их сумма имеет производную в точке x,
причем
производная
суммы
равна
сумме
производных:
( f ( x) g ( x)) f x g ( x)

11.

Теорема 2.
Если функция y=f (x) имеет производную в точке х, то
и функция y=k f(x) имеет производную в точке х,
причем
kf x kf x
Теорема 3.
Если функции y=f(x) и y=g(x) имеют производную в
точке x, то и их произведение имеет производную в
точке x, причем
( f ( x) g ( x)) f x g ( x) f ( x) g ( x)

12.

Теорема 4.
Если функции y=f(x) и y=g(x) имеют производную в
точке х и в этой точке g(x) ≠0,
то функция y
f x
g x
имеет производную в точке х, причем
f x
f x g x f x g x
2
g
x
g ( x)

13.

Теорема 5.
Если функция f(x) имеет производную в точке х0 , а
функция g имеет производную в точке y0 f x0 ,то
сложная функция h x g f x также имеет производную
в точке х0 , причем
h x0 g f x0 f x0

14.

С´=0, где С – константа.
(xn)´=n.xn-1 где n – натуральное
число
(ax)´=ax∙lna, где a>0, a≠1.
В частности, (ex)´=ex
(logax)´= 1 , где a>0, a≠1.
x ln a
1
В частности, (lnx)´= x .
(arcsinx)´=
1
(tgx)
2
cos x
1
(ctgx)
sin 2 x
(arctgx)´= 1
1
1 x2
(arccosx)´= -
(sinx)´=cosx.
(cosx)´= - sinx
1
1 x2
1 x2
(arcctgx)´= - 1
1 x2

15.

Примеры. Найти
производные функций
.
Решения
1.
f x x 3 x 4 ;
1.
f x 3x3 1 4 x 4 1 3x 2 4 x 3 .
2.
f x 3x 3 2 x 2 ;
2.
f x 3 3x3 1 2 2 x 2 1 9 x 2 4 x.
3.
f x x 2 x 3 x ;
3.
f x
x 2x x x 2x x 2 1 x 2x x x 2 3x 1
3
3
3 1
3
2 x3 x
x 6x2 1 .
2 x
4.
2x2 4
f x
;
5x 8
4.
2 x 4 5 x 8 2 x 4 5 x 8
4 x 5 x 8 2 x 4 5
f x
2
2
5x 8 2
2
5x 8 2
20 x 2 32 x 10 x 2 20 10 x 2 32 x 20
.
5x 8 2
5x 8 2
5.
f x 8 x 4 ;
3
2
2
2
5. f x 3 8 x 4 8 x 4 3 8 x 4 8 24 8 x 4 .

16. Применение производной к исследованию функции

Пример 1.
Функция y=f(x) определена на промежутке (-5;9). На рисунке
2 изображен график производной этой функции. Определите
число касательных к графику функции y=f(x), которые
наклонены под углом 45 0 к положительному направлению оси
абсцисс.
Рис.2

17.

Решение. Пусть α –угол касательной, проведенной к графику
функции y =f(x) в точке х 0 , и положительным
направлением оси абсцисс, тогда
tg f x0
Так как tg 45 1, то для
решения
задачи
достаточно определить
количество
точек
пересечения
графика
функции y f x
и
прямой у=1. Таких
точек четыре.
0
У=1
Рис.3

18.

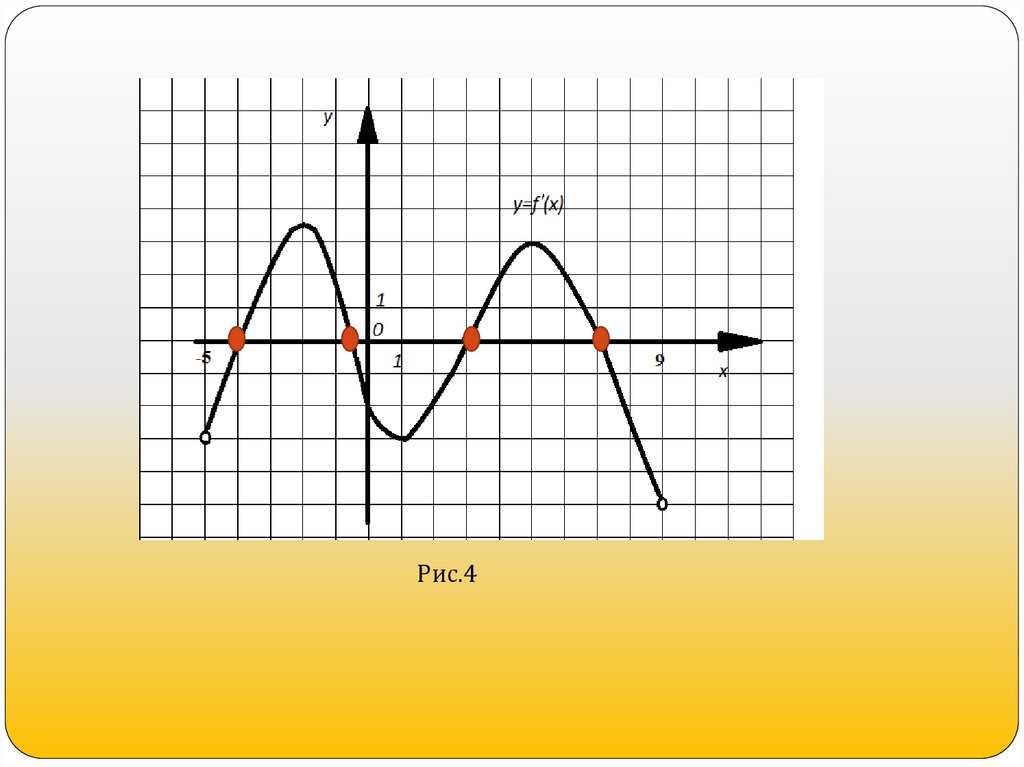
Пример 2.
На рисунке 2
изображен график производной
функции y=f(x) найдите абсциссу точки, в которой
касательная к графику y=f(x) параллельна прямой у=1
или совпадает с ней.
Решение. Так как касательная параллельна прямой
у=1, то ее угловой коэффициент равен 0 и тогда
производная равна 0. По графику (рис.2) определяем,
что производная обращается в ноль при х=-4; х=-0,5;
х=3; х=7.

19.

Рис.4

20.

Пример 3.
На рисунке 5 изображен график функции y=f(x),
определенной на промежутке . Определите количество
целых точек, в которых производная функции f(x)
положительна.
Рис.5

21.

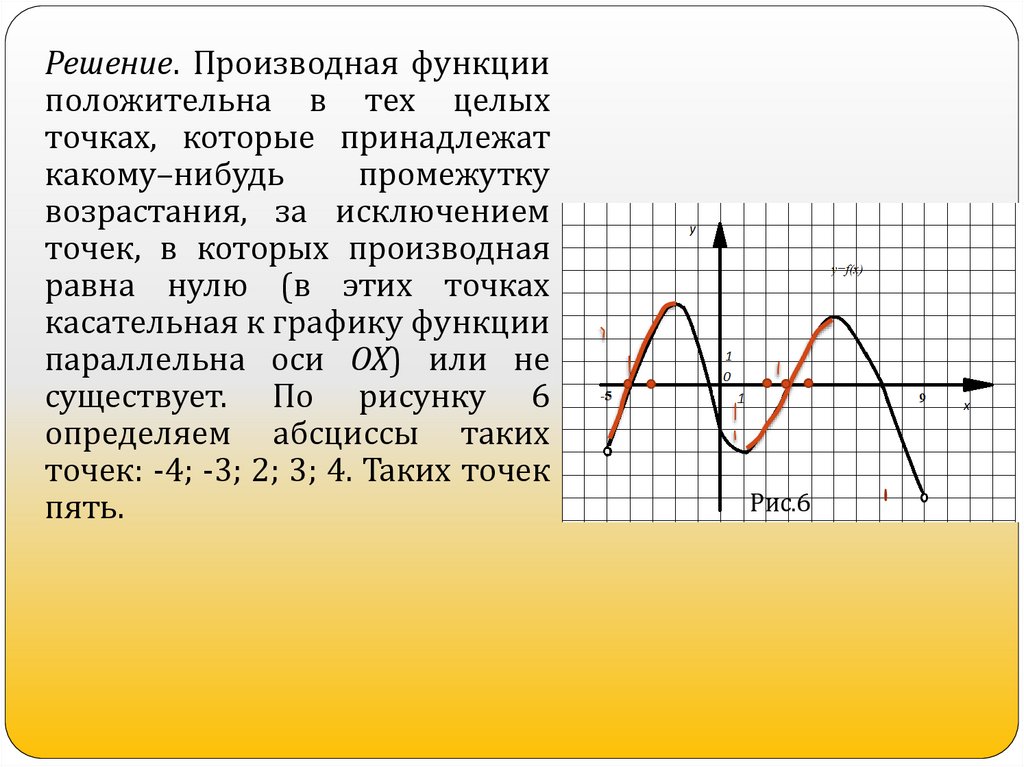
Решение. Производная функции
положительна в тех целых
точках, которые принадлежат
какому–нибудь
промежутку
возрастания, за исключением
точек, в которых производная
равна нулю (в этих точках
касательная к графику функции
параллельна оси ОХ) или не
существует. По рисунку 6
определяем абсциссы таких
точек: -4; -3; 2; 3; 4. Таких точек
пять.
Рис.6

22.

Пример 4.
На рисунке 5 изображен график функции y=f(x),
определенной на интервале (-5;9). Определите
количество целых точек, в которых производная
функции отрицательна.
Решение. Производная функции отрицательна в тех
целых точках, которые принадлежат какому–нибудь
промежутку убывания функции, за исключением
точек, в которых производная равна нулю (в этих
точках касательная к графику функции параллельна
оси ОХ) или не существует. По рисунку определяем
абсциссы таких точек: -1; 0; 6; 7; 8. Таких точек пять.

23.

Рис.6

24.

kкас. f x0
y f x
Рис.7

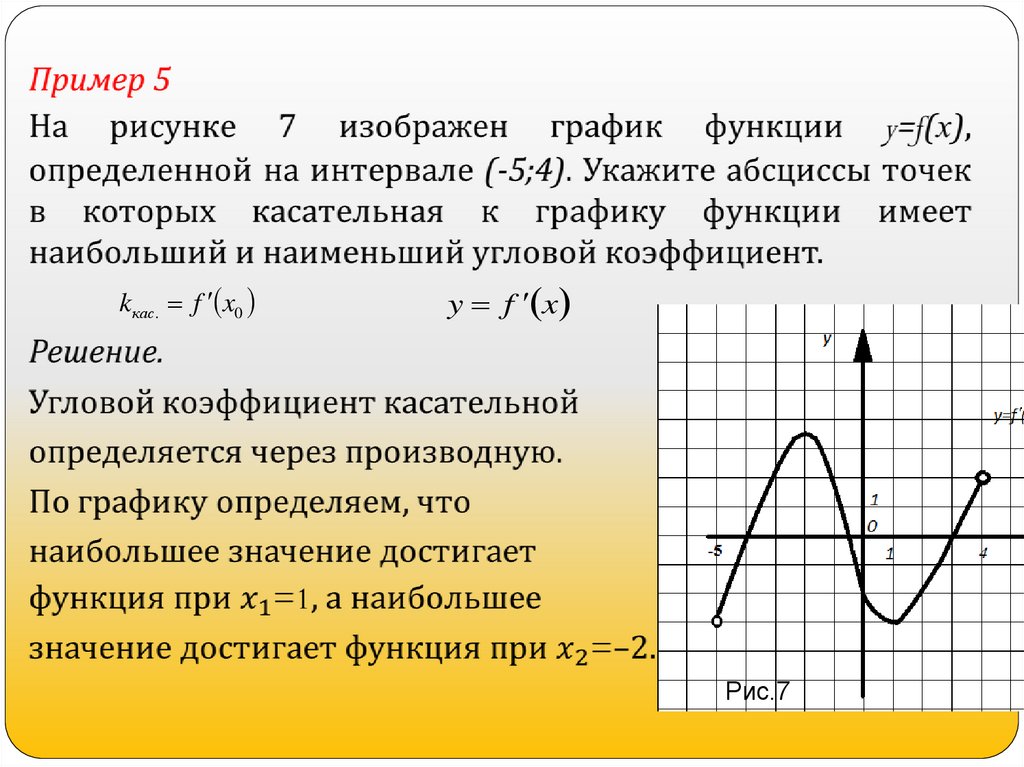
25.

Пример 6.
К графику функции y=f(x) проведена касательная в точке
x0 4 . На рисунке 8 изображен график
с . абсциссой
производной этой функции. Определите градусную меру
угла наклона касательной.
– угол наклона касательной в
данной точке к оси абсцисс. Так как
f 4 1
Решение. Пусть
Отсюда получаем
tg 1 , тогда
135 0
Рис. 8