Similar presentations:
Определение производной от функции
1. Определение производной от функции (К учебнику Колмогорова А.Н. «Алгебра и начала анализа 10-11»)
Цель презентации – обеспечить максимальную наглядностьизучения темы.
Выполнила
учитель математики МОУ «Курлекская СОШ»
Томского района Томской области
Логунова Людмила Васильевна
2006 год
2. Определение производной функции (Содержание)
I.II.
y
Геометрический смысл
x
отношения Слайд 3
Геометрический смысл
отношения y при х 0
Слайды 4,5
III.
IV.
V.
VI.
x
Геометрический смысл
производной функции Слайды 7,8
Определение производной
функции Слайд 6
Физический смысл Слайд 9
производной функции
Примеры вычисления
производной функции Слайд 10
3. Геометрический смысл приращения функции
yBC y
tg
B
y
y
y0
AC
Итак,
y
х
A
С
0
х0
Секущая
х
x
х
y
tg k
x
k – угловой
коэффициент
прямой(секущей)
х
y kx b
4. Геометрический смысл отношения при
yГеометрический смысл отношения
при х 0
x
y f (x)
y
Автоматический показ. Щелкните 1 раз.
y
x
tg k
y
k – угловой
коэффициент
прямой(секущей)
y
y kx b
х0
х
х
х
х
0
При
х стремится
0 угловой
коэффициен
секущей
угловому
Секущая
занять
положение т
касательной.
То к
есть,
касательная есть предельное положение секущей.
коэффициен
ту касательной.
0
5. Геометрический смысл отношения при
yГеометрический смысл отношения
при
x
y f (x)
Конспект
х 0
y
tg k
x
y
k – угловой
коэффициент
прямой(секущей)
y
y kx b
y
0
х0
х 0 х
х
Секущая стремится занять положение касательной. То есть,
касательная есть предельное положение секущей.
При х 0 угловой коэффициен т секущей к угловому
коэффициен ту касательной.
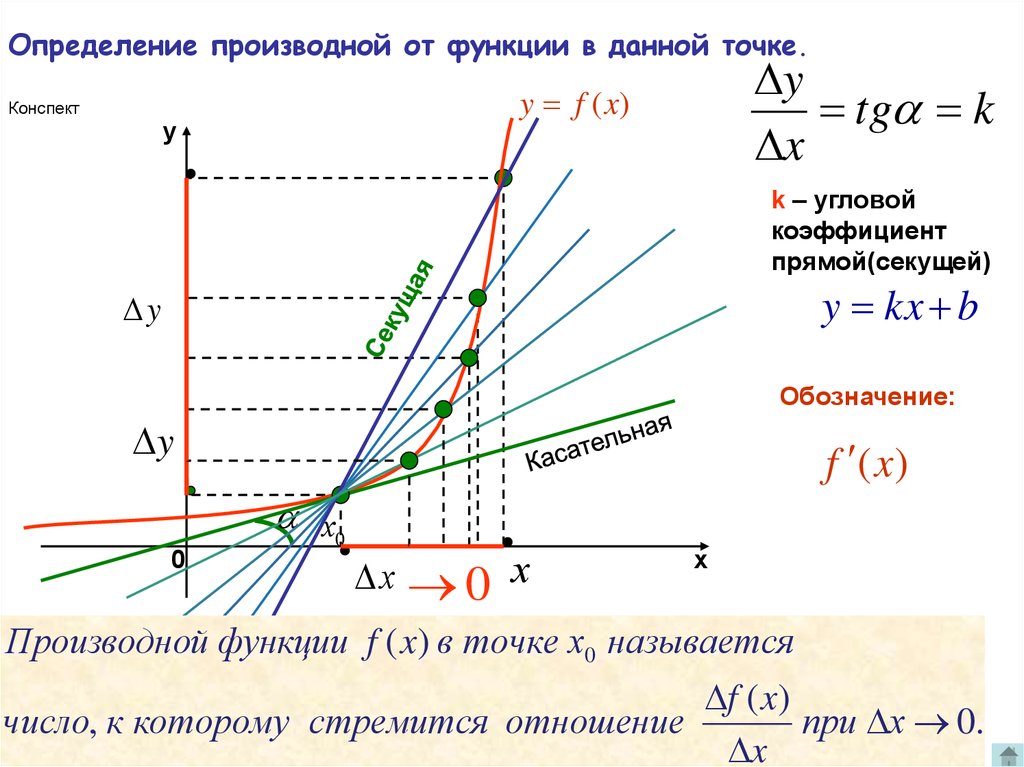
6. Определение производной от функции в данной точке.
ytg k
x
y f (x)
Конспект
y
k – угловой
коэффициент
прямой(секущей)
y kx b
y
Обозначение:
y
0
f (x)
х0
х 0 х
х
Производной функции f ( x) в точке х0 называется
f ( x)
число, к которому стремится отношение
при х 0.
x
7.
Конспектf ( x) tg k
y f (x)
y
k – угловой коэффициент
прямой(касательной)
y kx b
y
0
х0
х
0
х
х
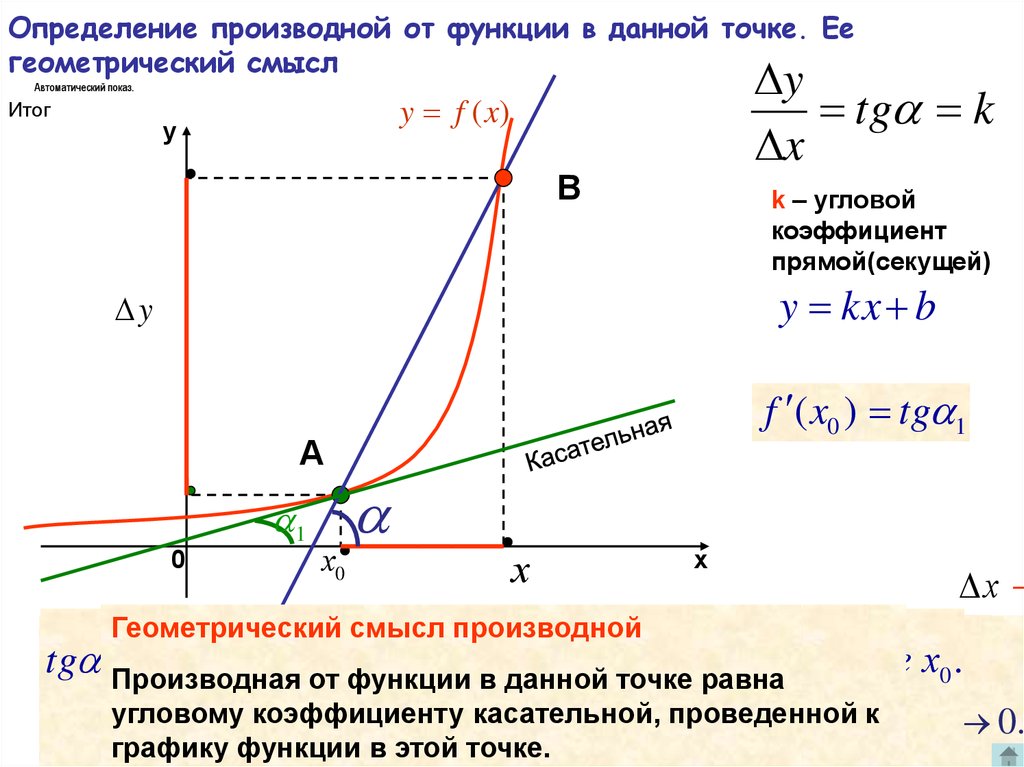
Геометрический смысл производной
Производная от функции в данной точке
равна угловому коэффициенту касательной,
проведенной к графику функции в этой
точке.
8. Определение производной от функции в данной точке. Ее геометрический смысл
Автоматический показ.y
tg k
x
y f (x)
Итог
y
В
k – угловой
коэффициент
прямой(секущей)
y kx b
y
f ( x0 ) tg 1
А
1
0
х0
х
х
х
Геометрический
смысл
производной
При
х
угловой
коэффициен
тх0секущей
к угловому
йy0функции
Производно
f
(
x
)
в
точке
называется
tg Производная
k
от
f (функции
x0 ) (производно
йточке
от равна
f ( x) в точке х0 .
в
данной
коэффициен
x ту касательной.
f ( x) к
угловому
коэффициенту
касательной,
проведенной
число, к которому стремится отношение
при х 0.
прив этой
х точке.
0
графику функции
x
9.
Физический смысл производной функциив данной точке
х
Vср.
t
Или, если х перемещение тела, а t промежуток времени ,
в течении которого выполнялось движение, то
х
средняя скорость движения на промежутке времени t.
t
При t 0 Vcр. к мгновенной скорости V (t ),
следовательно, V (t ) S (t ).
S (t ) V (t )
или х (t ) V (t )
Производная от функции в данной точке это
скорость изменения функции . f ( х) V ( x. )
10.
Пример вычисления производнойКонспект
Дано : f ( x) x 2 1.
Найдем f ( x) в точке х0 2, то есть f ( 2).
Решение
f ( x) f ( x0 x) f ( x0 )
f ( x0 x) f ( 2 x) ( 2 x) 2 1
4 4 x x 2 1 5 4 x x 2
f ( x0 ) ( 2) 2 1 4 1 5
f ( x) 5 4 x x 2 5 4 x x 2
f ( x) 4 x x 2
4 x
x
x
f ( x)
Если x 0, то
4, то есть f ( x) 4.
x
Ответ : f ( x) 4.








 mathematics
mathematics








