Similar presentations:
Функция Производная
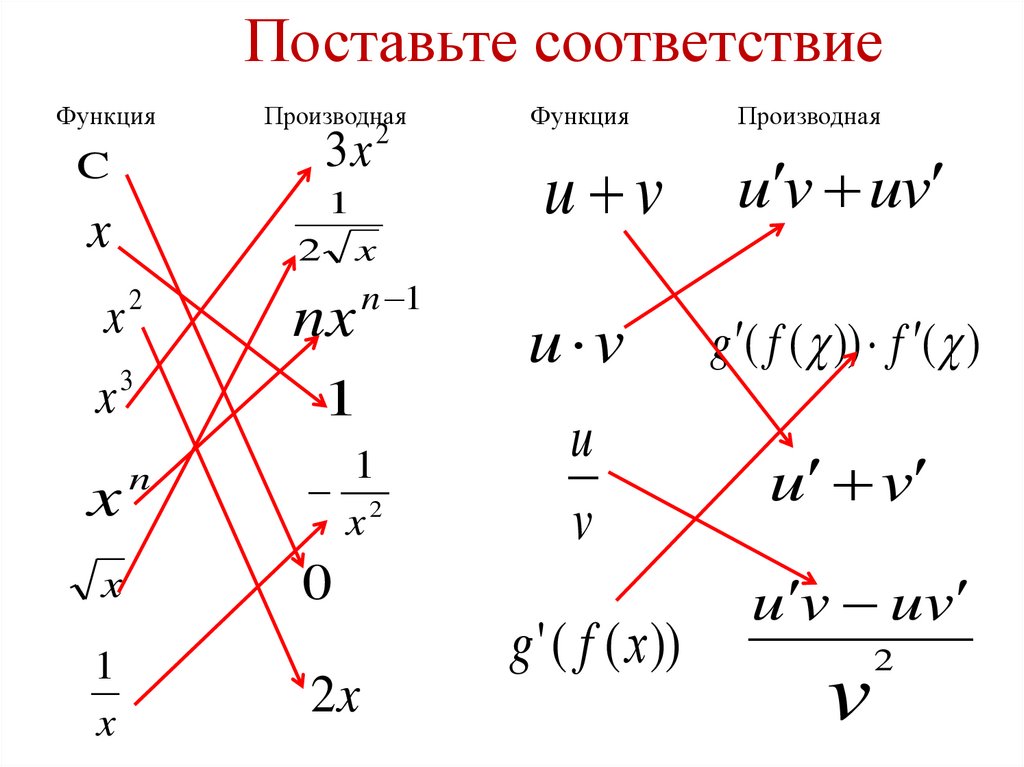
1. Поставьте соответствие
ФункцияПроизводная
3x
C
1
x
2
nx
3
1
x
x
1
x
n
Функция
u v
Производная
u v uv
x
2
x
x
2
n 1
1
2
x
0
2x
u v
g ( f ( )) f ( )
u
v
u v
g ' ( f ( х ))
u v uv
v
2
2. Найти производную функции
• f(x) = х4 - 4х3 + 6х2 _ 7• f(x) = 7x5 – 9x3 +3x -3,5
• f(x) = (x3 _ 2x)(x2 + 3)
x 5
• f(x) =
2x 4
2
3. Ответы
• f’(x) = 4x3 – 12x2 + 12x• f’(x) = 35x4 - 27x2 + 3
• f’(x) = 5x4 + 3x2 – 6
2 x 2 8 x 10
• f’(x) =
(2 x 4) 2
4.
Таблица производныхФункция
Производная
1
2
3
4
5
ax
ex
sin x
cos x
tg x
ax ln a
ex
cos x
-sin x
6
ctg x
7
arcsin x
8
ln x
9
loga x
10
11
12
13
14
sin (kx+b)
cos (kx+b)
akx+b
ekx+b
loga (kx+b)
1
cos 2 x
1
sin 2 x
1
1 x 2
1
x
1
x ln а
k cos (kx+b)
- k sin (kx+b)
k akx+b lna
k ekx+b
k
( kx b ) ln a
5.
Домашнее задание:§46
№ 831-839 (чётные),
№ 845(всё)
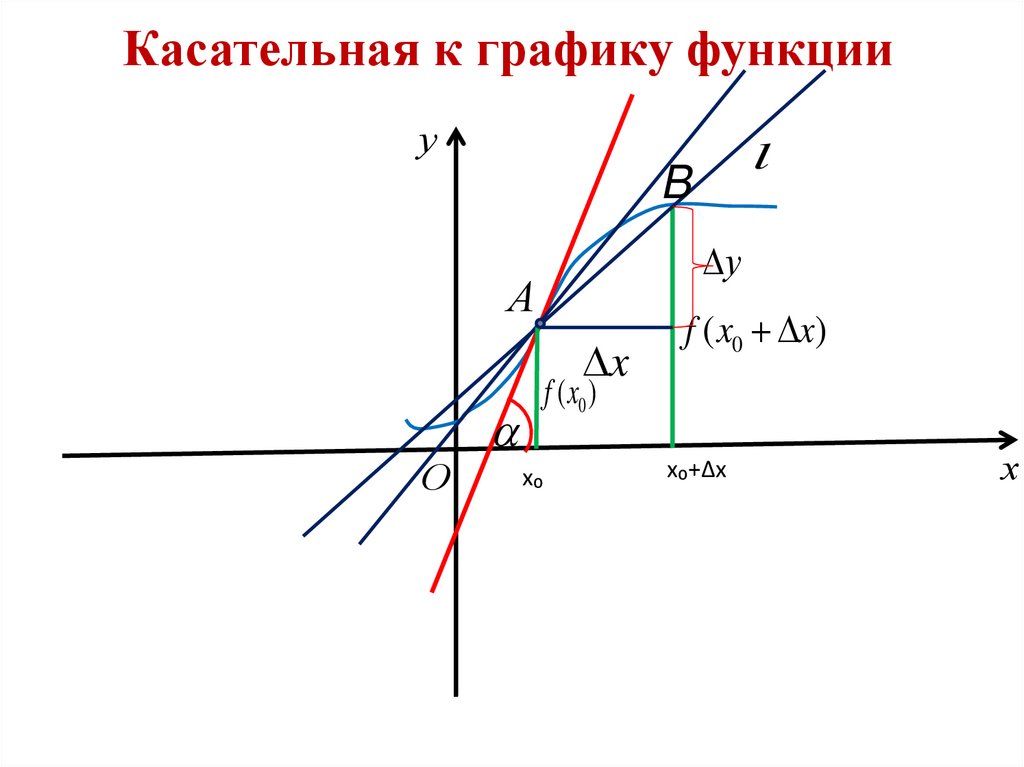
6. Касательная к графику функции
уl
B
у
А
x
f ( x0 )
О
f ( x0 x)
x₀
x₀+∆x
х
7. Геометрический смысл производной
Геометрический смысл производной состоит втом, что значение производной функции y=f(x)
в точке x0 равно угловому коэффициенту
касательной к графику функции в точке с
абсциссой x0 :
f ( x0 ) k tg
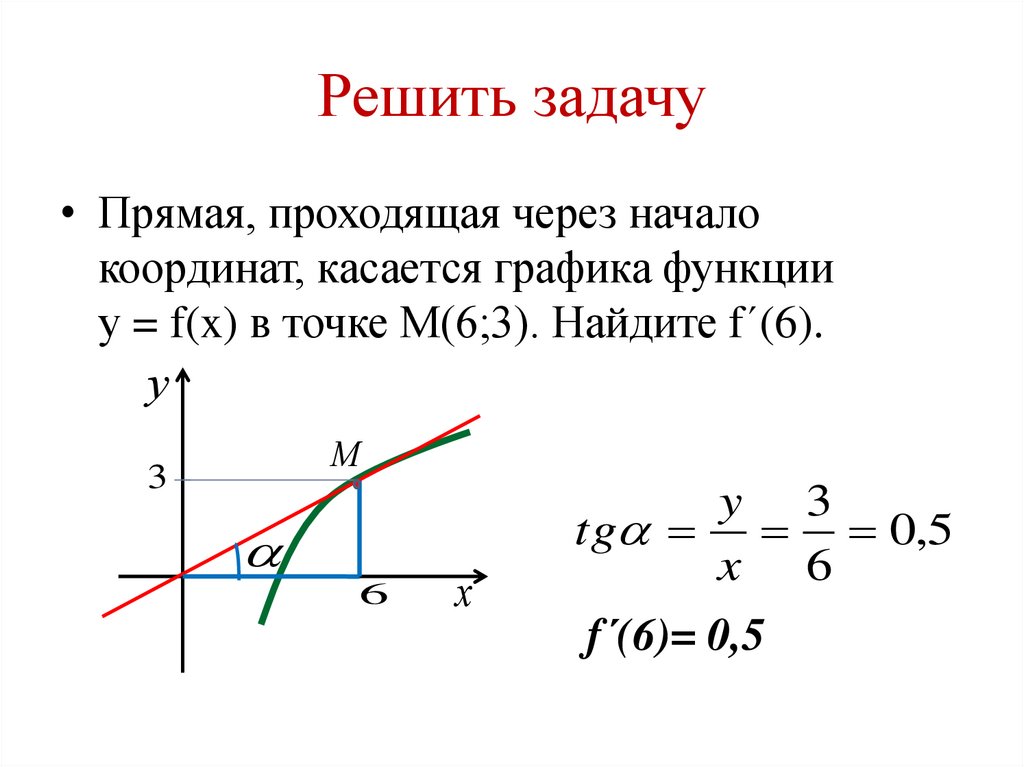
8. Решить задачу
• Прямая, проходящая через началокоординат, касается графика функции
у = f(x) в точке М(6;3). Найдите f´(6).
у
М
3
6
х
y 3
tg 0,5
x 6
f´(6)= 0,5
9.
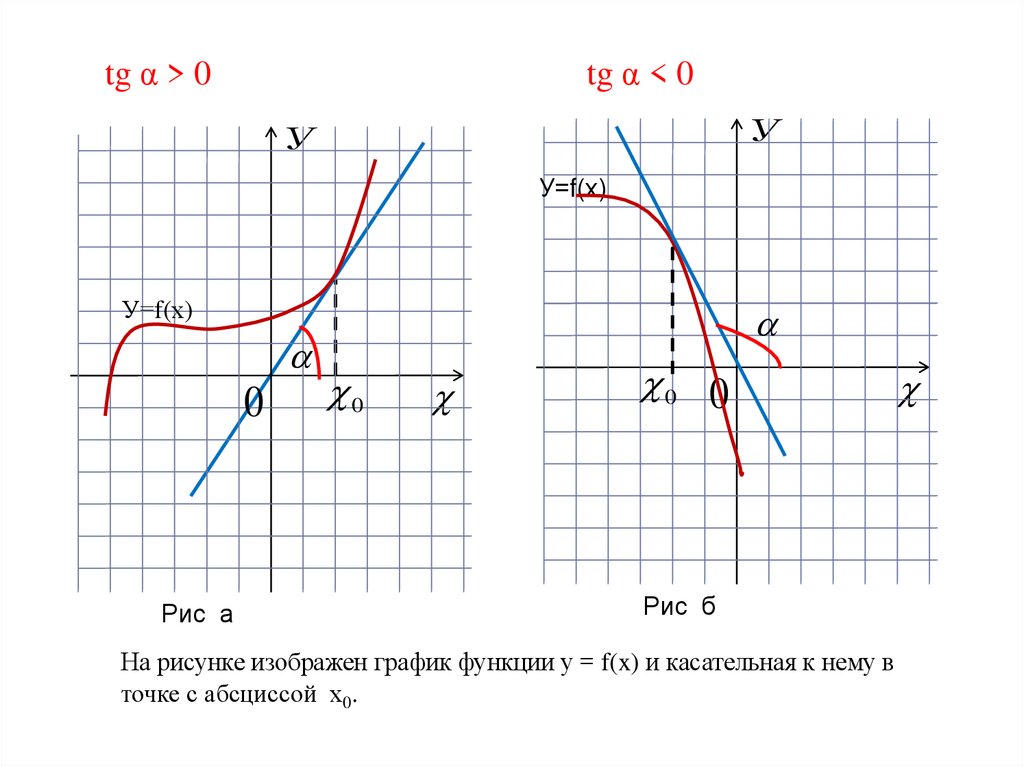
tg α > 0tg α < 0
У
У
У=f(х)
У=f(х)
0
Рис а
0
0 0
Рис б
На рисунке изображен график функции у = f(x) и касательная к нему в
точке с абсциссой х0.
10. Задача. Написать уравнение касательной
Дано: y f ( x), x0Алгоритм составления уравнения
касательной:
1.
2.
3.
4.
Вычислить f ( x0 )
Найти
f (x)
Вычислить f ( x0 )
Составить уравнение касательной:
y f ( x0 ) f ( x0 )( x x0 )
11. Найти уравнение касательной к графику функции
f ( x) x 2 x 1 x0 23
2
1. f ( x0 ) f (2) 2 2 2 1 1
3
2
2. f ( x) 3x 4 x
2
3. f ( x0 ) f (2) 3 2 4 2 4
2
4. y f ( x0 ) f ( x0 )( x x0 )
y 1 4( x 2)
y 4x 7







 mathematics
mathematics








