3.17M

Category: $mathematics$ mathematics

Производная функции

1. 2. Производная

Большинство функций, изучаемых в школьном
курсе алгебры и начал анализа, имеют себе в
пару другую функцию, называемую
производная функция от данной, или просто
производная.

3. Задача

На станции метро расстояние от тормозной
отметки до остановки первого вагона равно 80 м.
С какой скоростью поезд должен подойти к
тормозной отметке, если дальше он двигается
равнозамедленно с ускорением 1,6 м/с²?

4. Решение

Ѵ-?(мгновенная скорость в этот момент времени)
Тормозной путь
Где а- ускорение, t-время торможения.
S=80, a=1,6, поэтому
80=0,8t²
t=10 с
По формуле Ѵ=at.
Ѵ=1,6*10=16 м/с

5.

Задачи, приводящие к понятию
производной

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

C 0
x 1
(kx b) k
( x )
1
2 x
(x ) n x
n
n 1

18.

(sinx ) cosx
(cosx ) sinx
1
(tgx )
2
cos x
1
(ctgx )
2
sin x

19.

20.

21.

22.

23.

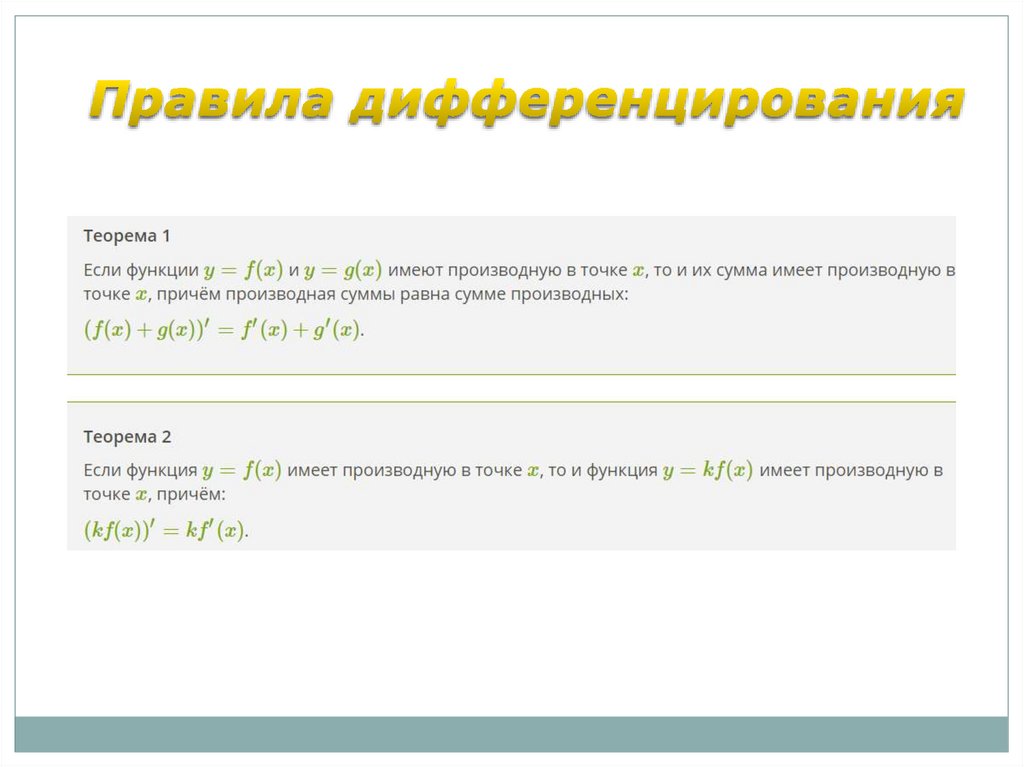
Формулами дифференцирования обычно называют формулы для
нахождения производных конкретных функций, например:
(u v) u v
(С u) C u
(u v) u v u v
u u v u v
2
v
v

24.

25.

1) f ( x) 3x 5 x 2 x 4 x 6
7
5
3
Решение
7
5
3
f (x) 3 (x ) 5 (x ) 2 ( x ) 4 ( x) 6
3 7x 5 5x 2 3x 4 1 0
f (x)
6
4
2
f ( x) 21x 25x 6 x 4
6
4
2

26.

2) f ( x) (5 sin x x )
6
Решение
f ( x) (5 sin x x )
6
5(sin x) ( x )
6
5 cos x 6 x
5

27.

3) f ( x) 12 x tg ( x)
Решение
f (x) 12 (x ) - (tg(x))
1
f (x) 12 1 2
cos x
1
f (x) 12 2
cos x

28.

f(x) x sin x
4
Решение
4
4
f (x) (x ) sinx x (sin x)
f (x) 4x sin x x cos x
3
4

29.

2x
5) f ( x)
4x 3
Решение
(2x) (4x 3) - 2x (4x 3)
f (x)
2
(4x 3)
2(4x 3) - 2x 4 8 x 6 8 x
6
f (x)
2
2
(4x 3)
(4 x 3)
(4 x 3) 2

30.

31.

32.

33.

34.

35.

f(g(x)) f (x) g (x)
Пример
f ( x) ( 5 x 11)
4
Решение
4
f (x) ((-5x 11) ) (5x 11)
f(x) 4 (-5x 11) ( 5) 20 ( 5x 11)
3
3

36.

f(x) cos 5 x
Решение
f (x) (cos5x) (5x) -sin5x 5
f (x) -5sin5x

37.

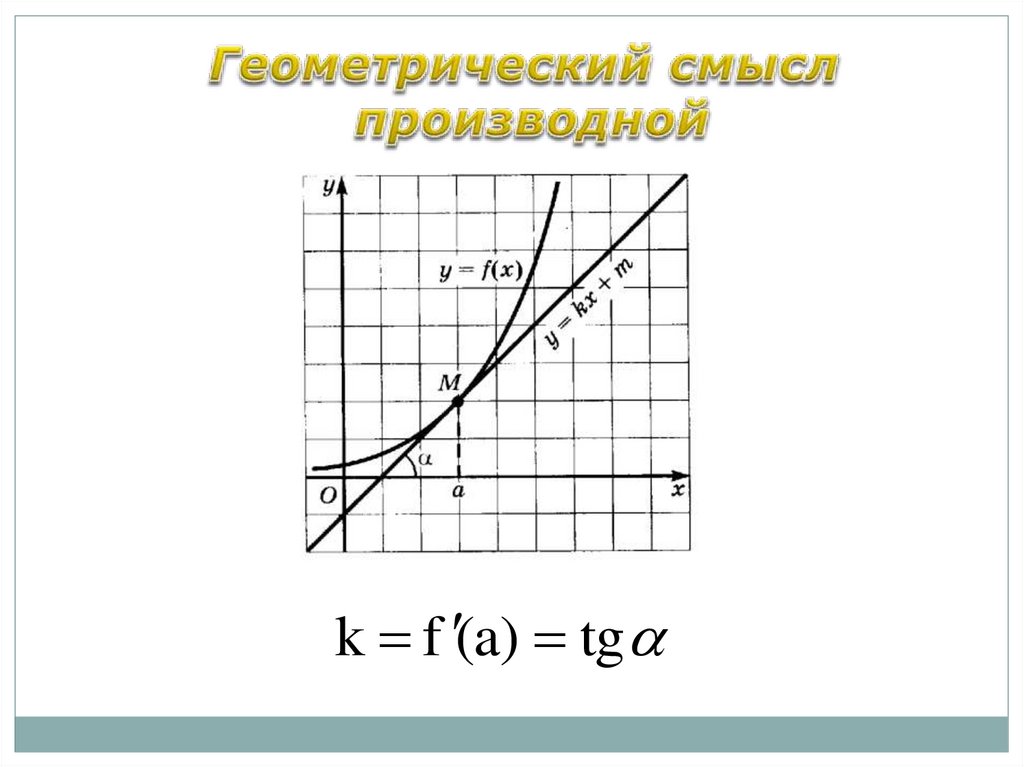
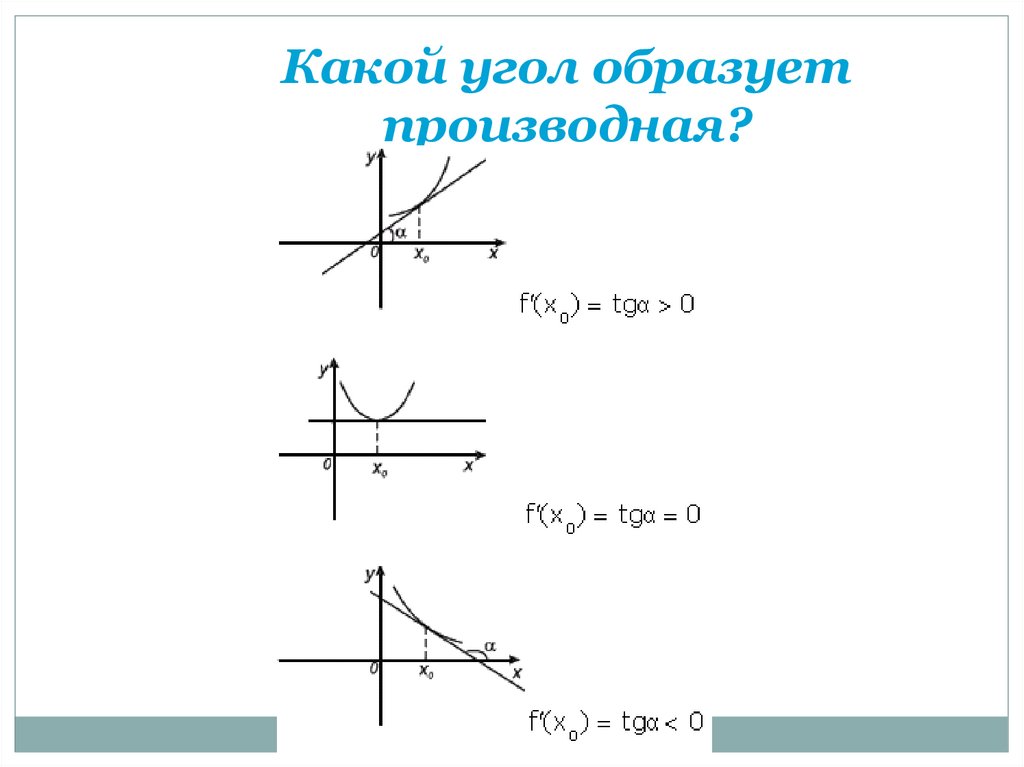
k f (a) tg

38. Какой угол образует производная?

39. Производная на ЕГЭ (задача В8)

f (x 0 ) tg
tg 0,2
f ( x0 ) tg
tg 0,2
Используя определение
f (x0 ) tg получим

40. Производная на ЕГЭ (задача В8)

На рисунке изображены график функции y = f(x) и касательная к
нему в точке с абсциссой x0 Найдите значение производной
функции y = f(x) в точке x.0
Ответ:
tg 1

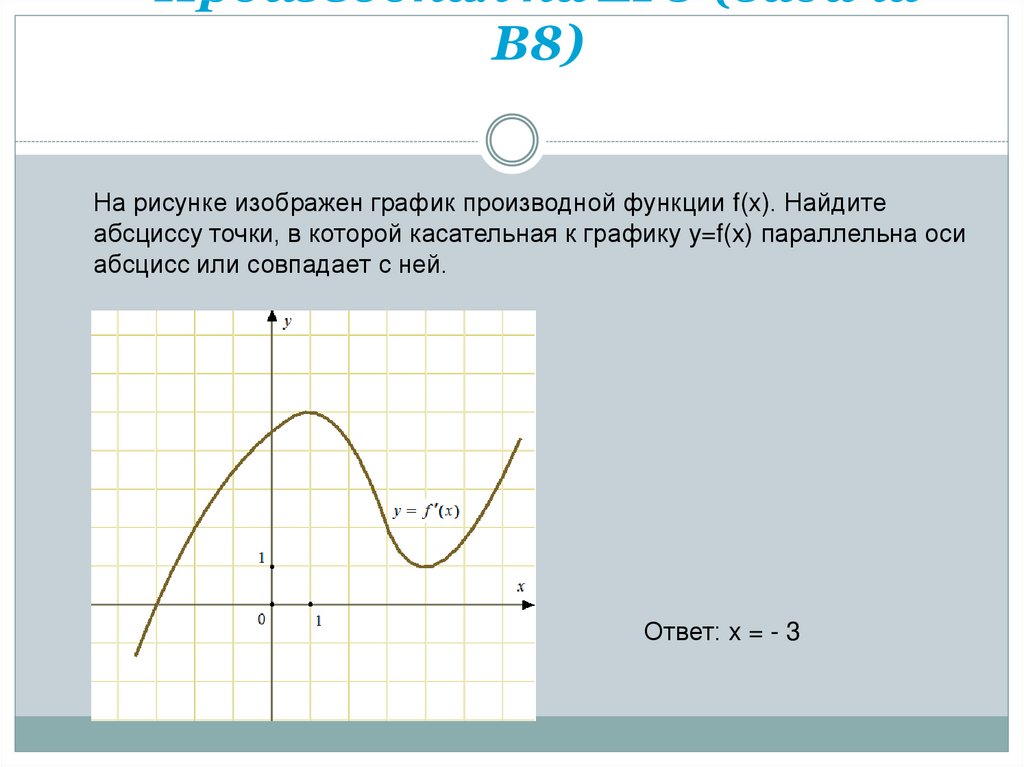
41. Производная на ЕГЭ (задача В8)

На рисунке изображен график производной функции f(x). Найдите
абсциссу точки, в которой касательная к графику y=f(x) параллельна оси
абсцисс или совпадает с ней.
Ответ: x = - 3

42.

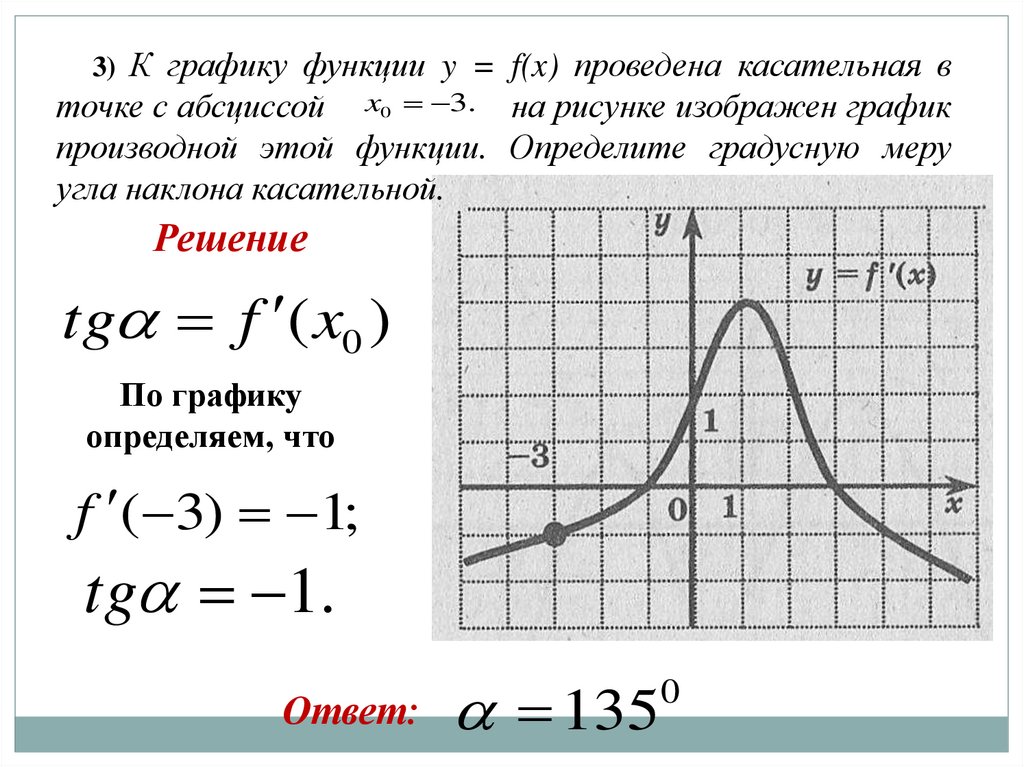
3) К графику функции y = f(x) проведена касательная в
точке с абсциссой x0 3. на рисунке изображен график
производной этой функции. Определите градусную меру
угла наклона касательной.
Решение
tg f ( x0 )
По графику
определяем, что
f ( 3) 1;
tg 1.
Ответ:
135
0

43.

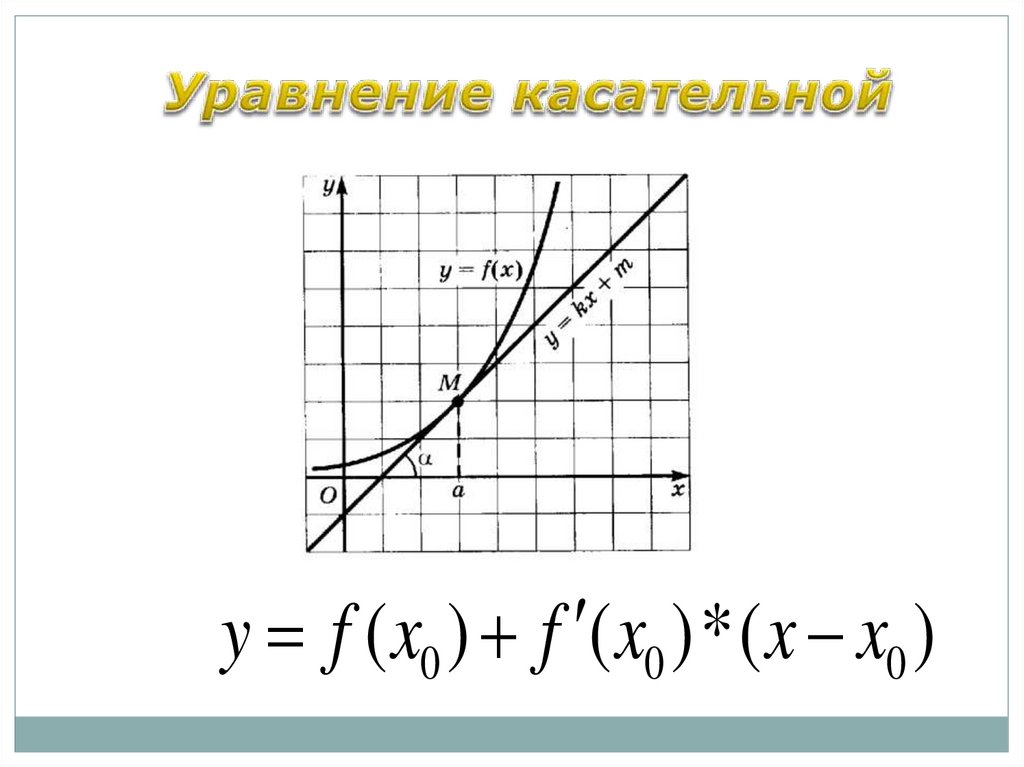
y f ( x0 ) f ( x0 ) * ( x x0 )

44.

Пример
Составить уравнение касательной, проведенной к
графику
функции
графика с абсциссой
y 2 x3 5x 2 2
точке
x0 2.
Решение
y f ( x0 ) f ( x0 ) * ( x x0 )
y ( x) 2 * ( x 3 ) 5 * ( x 2 ) 2 2 * 3x 2 5 * 2 x 0
6 x 2 10 x
y ( x0 ) y (2) 2 * 23 5 * 2 2 2 6
y ( x0 ) y (2) 6 * 2 2 10 * 2 4
y 6 4 * ( x 2) 6 4 x 8 4 x 14
Ответ:
y 4 x 14