Similar presentations:
Производная функции
1.
(По материалам, изученным в 10 классе).2.
C 0x 1
(kx b) k
( x )
1
2 x
(x ) n x
n
n 1
3.
(sinx ) cosx(cosx ) sinx
1
(tgx )
2
cos x
1
(ctgx )
2
sin x
4.
(u v) u v(С u) C u
(u v) u v u v
u u v u v
2
v
v
5.
1) f ( x) 3x 5 x 2 x 4 x 67
5
3
Решение
7
5
3
f (x) 3 (x ) 5 (x ) 2 ( x ) 4 ( x) 6
3 7x 5 5x 2 3x 4 1 0
f (x)
6
4
2
f ( x) 21x 25 x 6 x 4
6
4
2
6.
2) f ( x) (5 sin x x )6
Решение
f ( x) (5 sin x x )
6
5(sin x) ( x )
6
5 cos x 6 x
5
7.
3) f ( x) 12 x tg ( x)Решение
f (x) 12 (x ) - (tg(x))
1
f (x) 12 1 2
cos x
1
f (x) 12 2
cos x
8.
f(x) x sin x4
Решение
4
4
f (x) (x ) sinx x (sin x)
f (x) 4x sin x x cos x
3
4
9.
2x5) f ( x)
4x 3
Решение
(2x) (4x 3) - 2x (4x 3)
f (x)
(4x 3)2
2(4x 3) - 2x 4 8 x 6 8 x
6
f (x)
2
2
(4x 3)
(4 x 3)
(4 x 3) 2
10.
f(g(x)) f (x) g (x)Пример
f ( x) ( 5 x 11)
4
Решение
4
f (x) ((-5x 11) ) (5x 11)
f(x) 4 (-5x 11) ( 5) 20 ( 5x 11)
3
3
11.
f(x) cos 5 xРешение
f (x) (cos5x) (5x) -sin5x 5
f (x) -5sin5x
12.
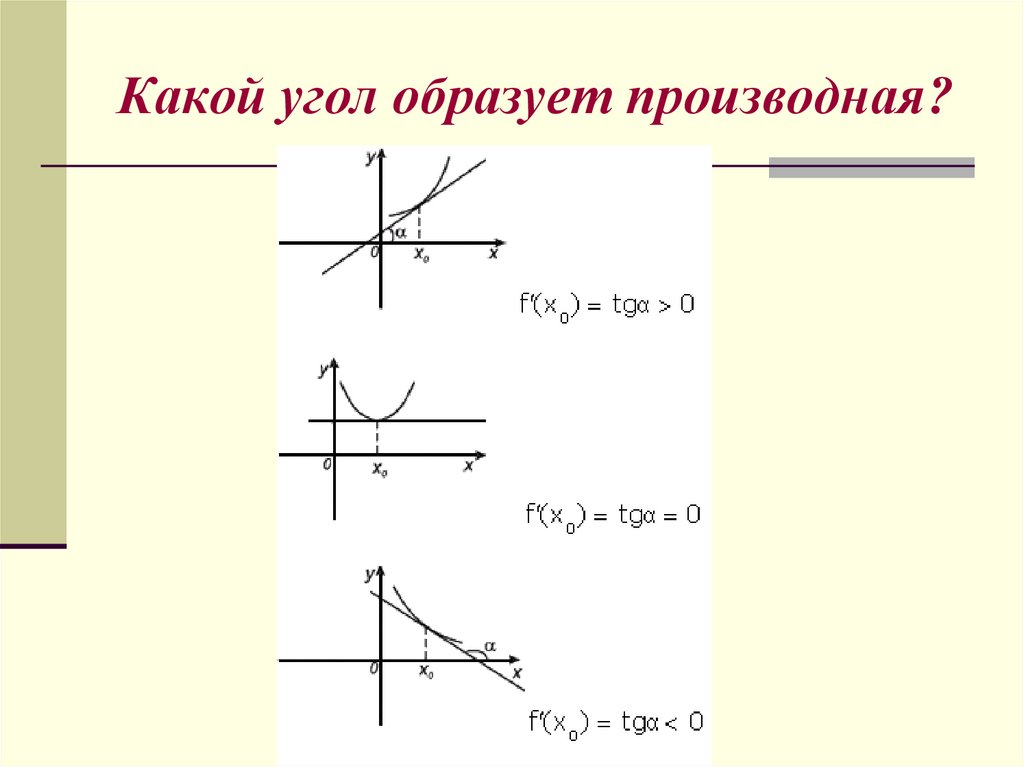
k f (a) tg13. Какой угол образует производная?
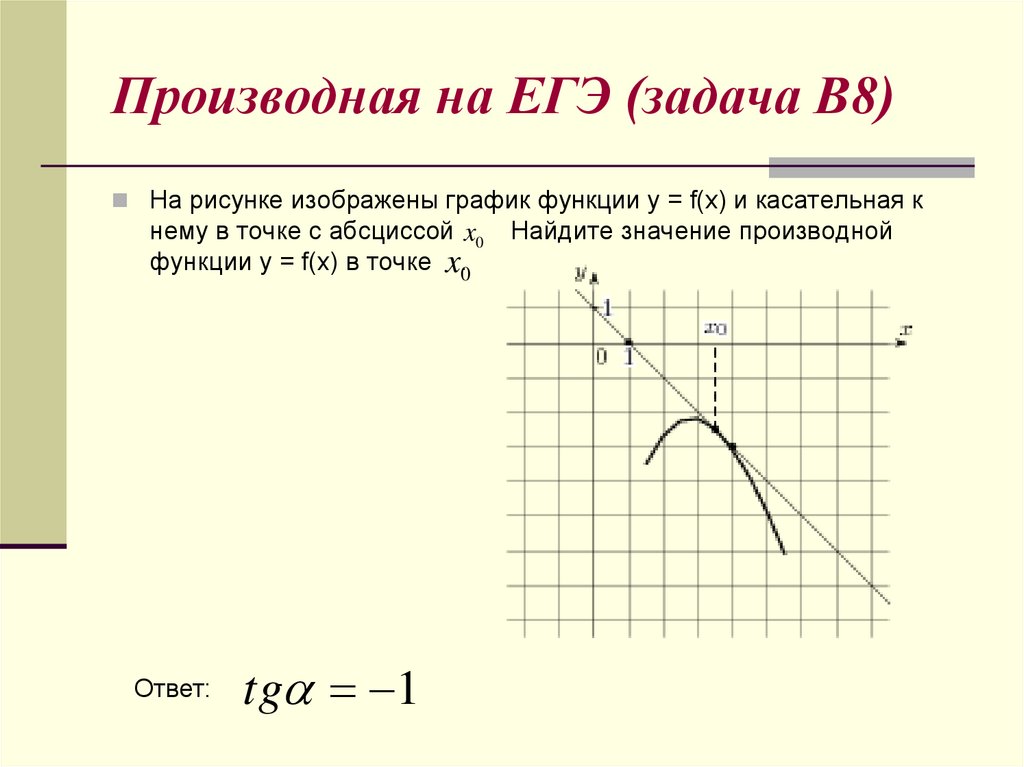
14. Производная на ЕГЭ (задача В8)
На рисунке изображены график функции y = f(x) и касательная кнему в точке с абсциссой x0
функции y = f(x) в точке x.0
Ответ:
tg 1
Найдите значение производной
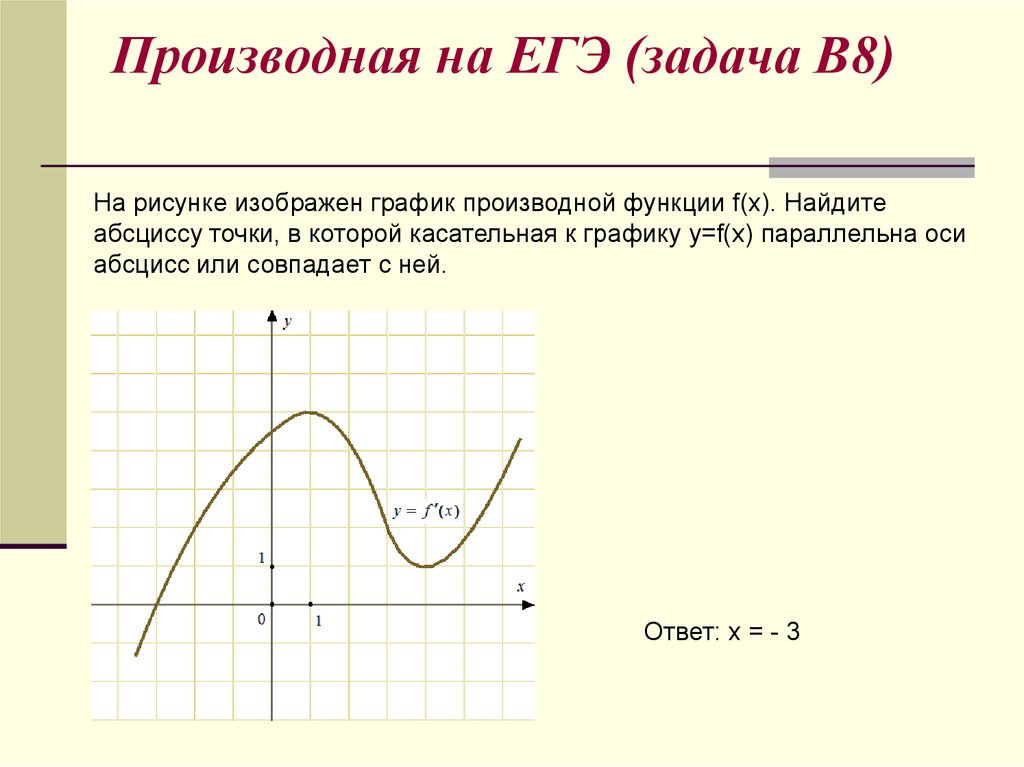
15. Производная на ЕГЭ (задача В8)
На рисунке изображен график производной функции f(x). Найдитеабсциссу точки, в которой касательная к графику y=f(x) параллельна оси
абсцисс или совпадает с ней.
Ответ: x = - 3
16.
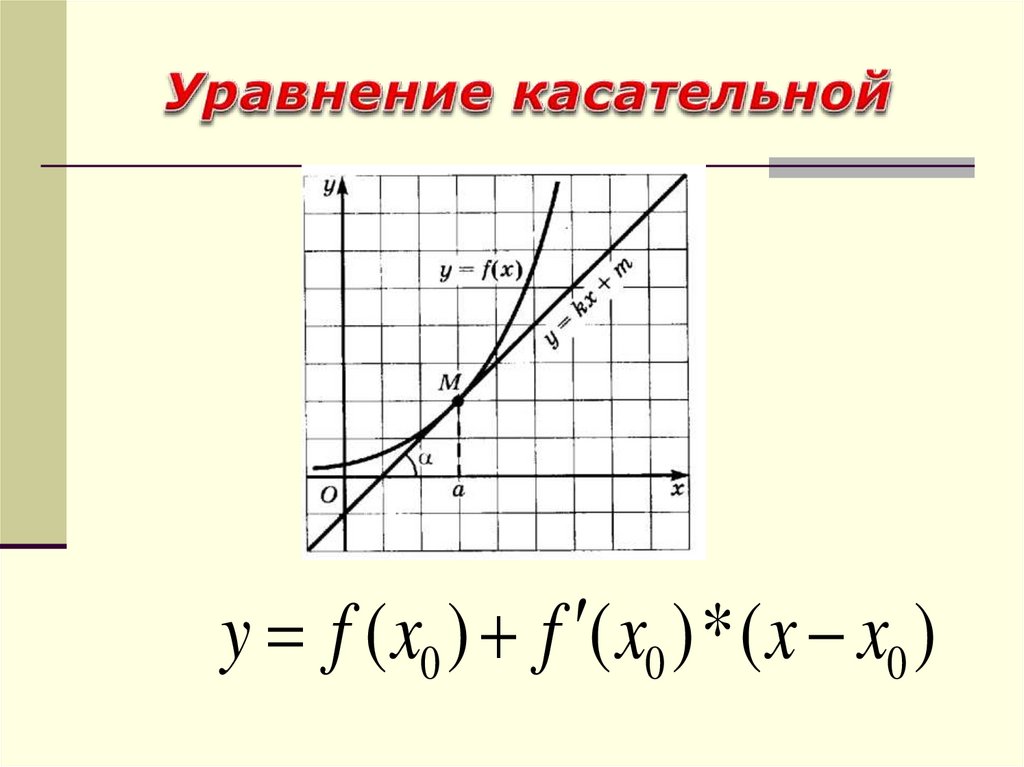
y f ( x0 ) f ( x0 ) * ( x x0 )17.
ПримерСоставить уравнение касательной, проведенной к
графику
функции
графика с абсциссой
y 2 x3 5x 2 2
точке
x0 2.
Решение
y f ( x0 ) f ( x0 ) * ( x x0 )
y ( x) 2 * ( x 3 ) 5 * ( x 2 ) 2 2 * 3x 2 5 * 2 x 0
6 x 2 10 x
y ( x0 ) y (2) 2 * 23 5 * 2 2 2 6
y ( x0 ) y (2) 6 * 2 2 10 * 2 4
y 6 4 * ( x 2) 6 4 x 8 4 x 14
Ответ:
y 4 x 14
18.
S (t ) v(t )v (t ) a(t )
19.
ПримерМатериальная точка движется по прямой
так, что ее скорость в момент времени t равна
v(t ) t 3 2t.
Найдите ускорение точки
времени t = 3.
Решение
a (t ) v (t )
v (t ) (t 2t ) 3 * t 2
3
2
v (3) 3 * 3 2 25
2
Ответ:
a (3) 25
в
момент
20.
Найдите наибольшее значение функцииy x 3x 4
3
на отрезке
1) y ( x) 3 x 3
,
2 ) y ( x) 0
,
2
2;0
y ( 2) ( 2) 3 3( 2) 4
8 6 4 2
y ( 1) ( 1) 3( 1) 4
3
3x2 3 0
1 3 4 6
3( x 2 1) 0
y (0 ) 4
x 1 2;0
x 1
Ответ: 6
21.
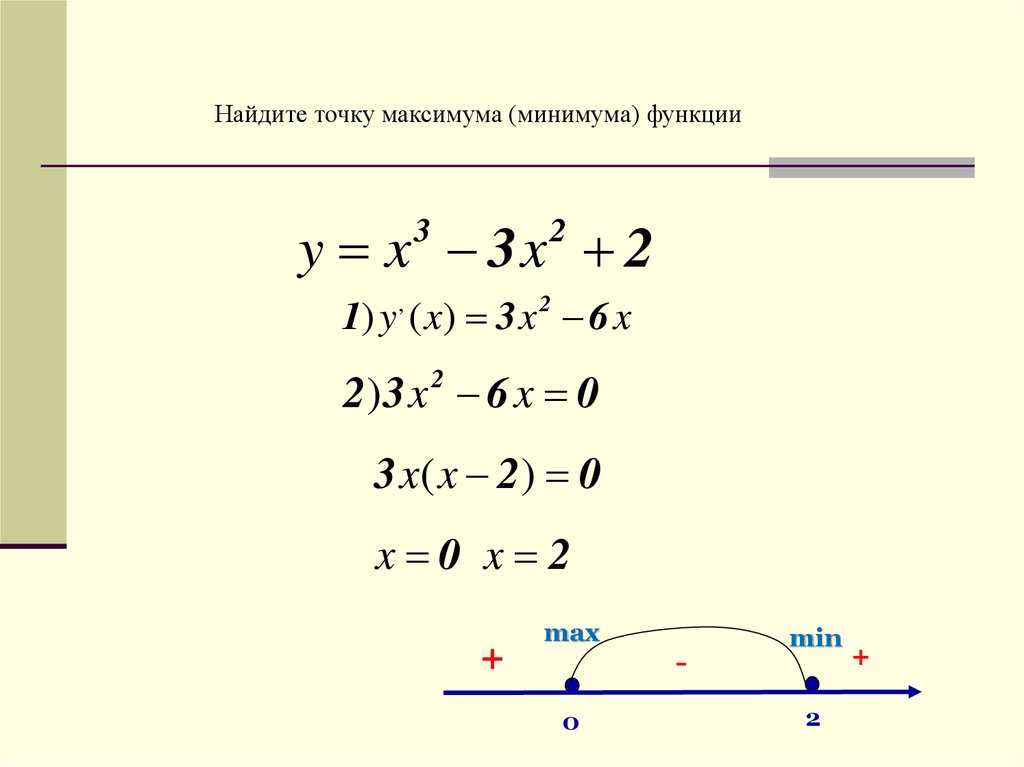
Найдите точку максимума (минимума) функцииy x 3x 2
3
2
1) y , ( x) 3 x 2 6 x
2) 3 x 2 6 x 0
3 x( x 2) 0
x 0 x 2
+
max
0
min
2
+
22.
Постройте график функции , используя подробную схему построения. схему построения.1)
2) Функция не является ни четной, ни нечетной, т. к.
3) х = 1 – вертикальная асимптота
4)
f’(x) = 0 при х = 2, х = 0.
х = 2, х = 0 – стационарные точки.
23.
.5) f’(x)>0 при .
Так как в точках х = 0, х = 2 функция
непрерывна,
то эти точки также включаются в промежутки возрастания.
f’(x) <0 при х(0,1);х(1;2) . Так как в точках х = 0, х = 2 функция
непрерывна,
то эти точки также включаются в промежутки убывания.
Так как в точке х = 0 производная меняет знак с «+» на «-»,
то х = 0 – точка максимума.
Так как в точке х = 2 производная меняет знак с «-» на «+»,
то х = 2 – точка минимума.
х = 1 – не является точкой экстремума
6) Найдем интервалы выпуклости функции.
и. f ’’(x)=2(х-1)3
; f ’’(x) <0 при х <1
при х(-∞;1) функция выпукла вверх.
; f ’’(x) >0 при х ) >1
при х(1;+∞) функция выпукла
вниз.
24.
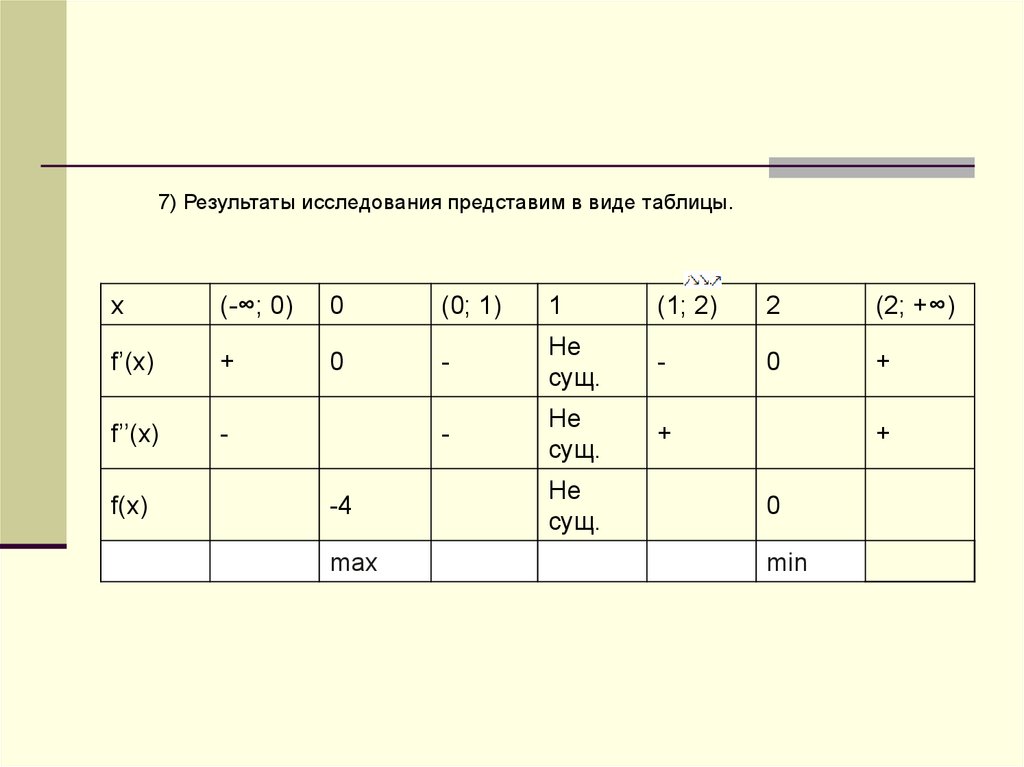
7) Результаты исследования представим в виде таблицы.x
(-∞; 0)
0
(0; 1)
1
(1; 2)
2
(2; +∞)
f’(x)
+
0
-
Не
сущ.
-
0
+
f’’(x)
-
-
Не
сущ.
+
f(x)
-4
max
Не
сущ.
+
0
min
25.
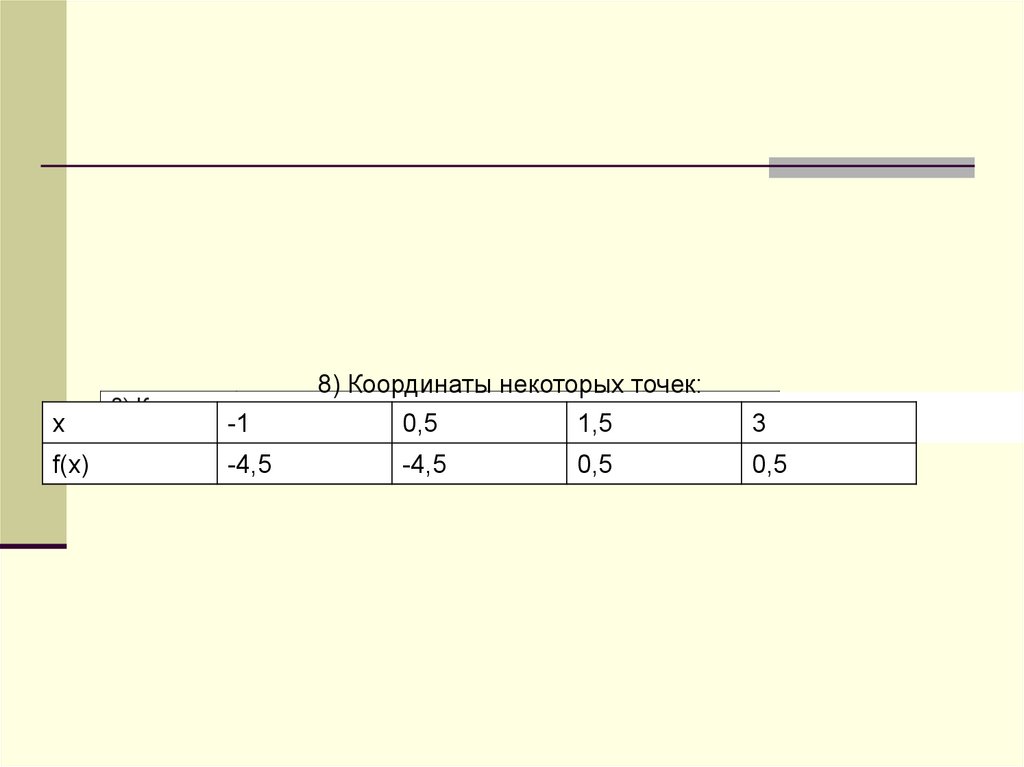
x8) Координаты некоторых точек:
3
8)
некоторых точек:
x Координаты
-1
0,5
-1
0,5 график1,5
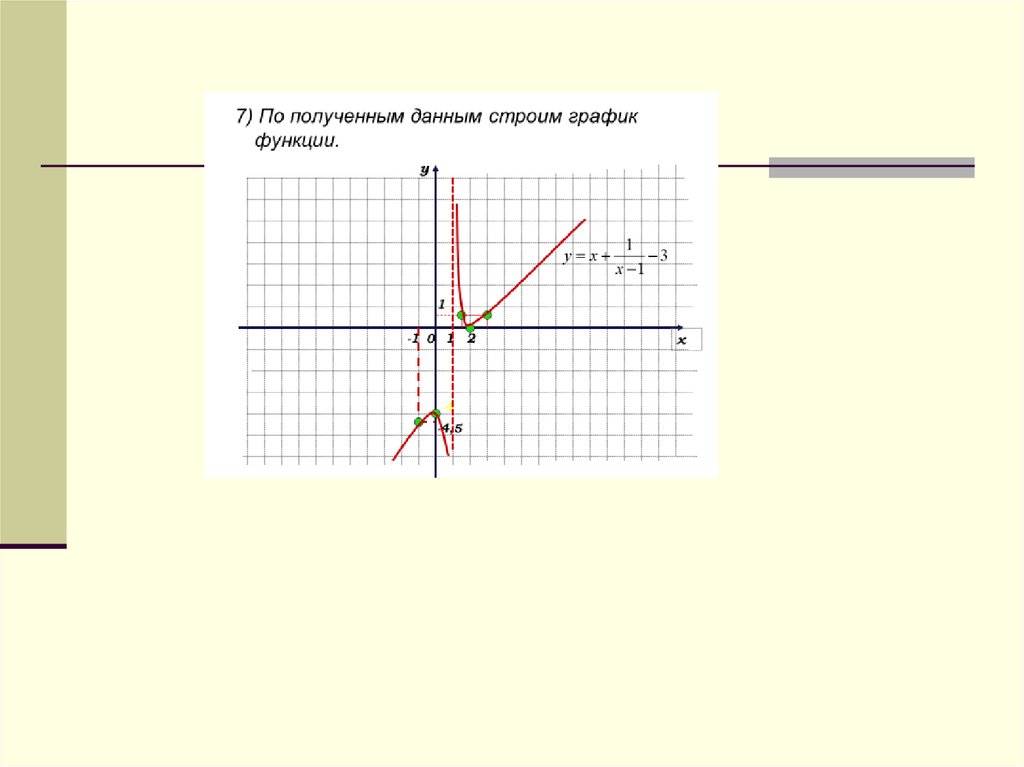
9) По полученным
данным строим
(рис.1,5
2)
f(x) f(x)
-4,5
-4,5
-4,5
-4,5
0,5 0,5
0,5
3
0,5


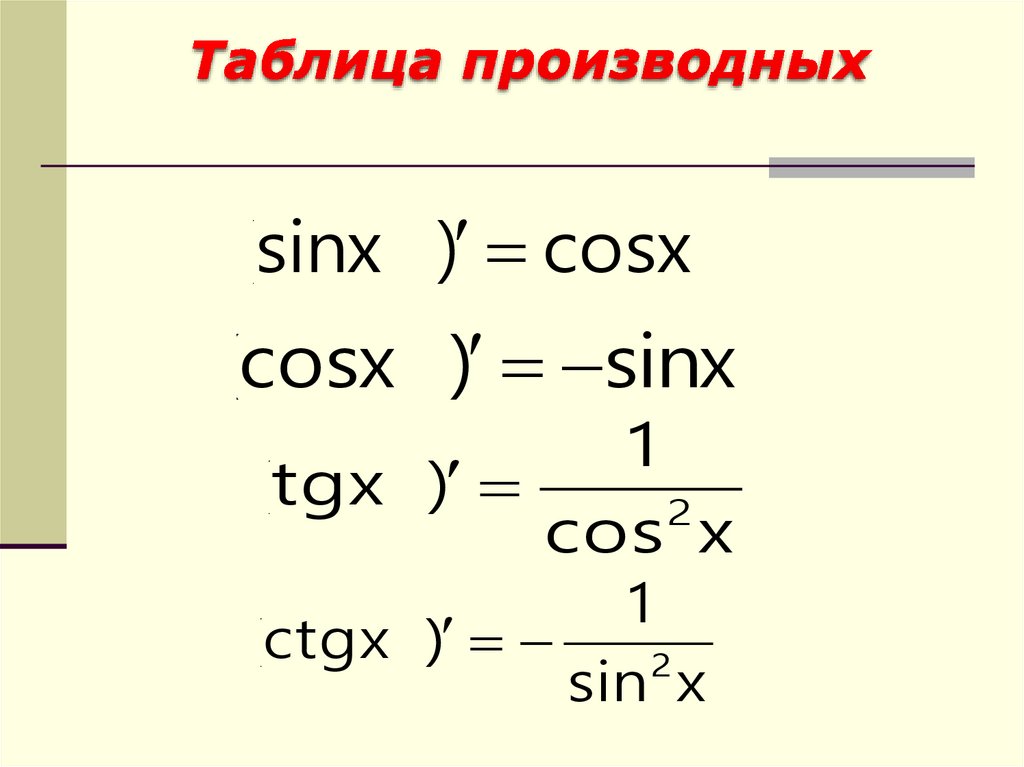















 mathematics
mathematics








