тригонометрические функции

1.

В презентации представлен проект Т.П. Ефремовой
«Тригонометрические функции». Данную работу можно использовать на
уроках алгебры для 9-10 классов.
Работа выполнена в прoграмме PowerPoint.
Проект будет интересен учителям при объяснении нового материала, а
также при систематизации и обобщении его.
Для учащихся эта работа может быть пособием при самостоятельном
изучении темы «Тригонометрические функции», поможет понять
взаимосвязь графического и аналитического решений
тригонометрических уравнений и неравенств.
Вторая СПб Гимназия
Санкт-Петербург, Казанская,27

2.

π
90° 2
1 F
М
R=1
-1
B ABО : ОА 1
AB АВ
sin
АВ ОМ
OA
1
OB ОВ
ОВ
OA
1
По теореме Пифагора :
sin 2 cos 2 1
C
Д
ctg
A cos ; sin
180°π
cos
tg
0
0 1
B N К 360°2π
В ОСК :
tg
270° -1
3π
2
КС КС
КС
ОК
1
В ODN :
ON ON
ctg
ON FD
DN
1
tg
sin
cos
ctg
cos
sin

3. Определения

Синусом числа х называется ордината точки А,
косинусом числа х называется абсцисса точки А,
которая получена поворотом начальной точки
единичной окружности на угол х.
Тангенсом числа х называется отношение
синуса числа х к косинусу числа х,
котангенсом числа х называется отношение
косинуса числа х к синусу числа х.
Функции у=sin x, у=cosx, у=tgx и у= ctg x
называются тригонометрическими

4.

tg
180 радиан
1
180
180
180
-1
3
1 рад
3
4
180
180
рад
3
2
1
cos 120 cos 60
2
sin 120 sin 60
sin 135 sin 45
90
2
3 120
3
3
1
1
60 3
3
2
2
2
135
45
4
2
1
2
1
2
3
2
7 210
6
2
2
sin 180 sin
cos 180 cos
ctg
3
3
0
-1 3 2
2
2
3
30
6
1
2
180
2
cos 135 cos 45
3
3
5
6 150
1
sin 150 sin 30
2
cos150 cos 30
2
3
5 225
240
4
4
3
2
2
3
2
-1 270
3
2
360 2
3
2
1
11
330
6
3
3
1
2
2
2
315 7
300
5
3
sin 90 cos
4
-1
3
cos 90 sin
tg 90 ctg

5.

1 2
x
y
М
1
0 2
0
-1
-y
-1 3
1
2
0
-x
М1
2
3
2
-1
2
1) D y ;
2) E y 1;1
3)T 2
4)Функция нечетная
а) D y симметрична
относительно точки О
б ) y x y x
5) y 0 при х n
6) унаиб. 1 при х
2 n
2
7) yнаим. 1 при х
2
2 n
8) монотонность
а)функция на 2 n; 2 n
2
2
3
б )функция на 2 n;
2 n
2
2
9)промежутки знакопостоянства
а) у 0 на 2 n; 2 n
б ) у 0 на 2 n;2 2 n
n Z
2

6.

1 2
1
x
1 0
-1
2
y
0
2
0
-x
-1
2
-1
3 2
2
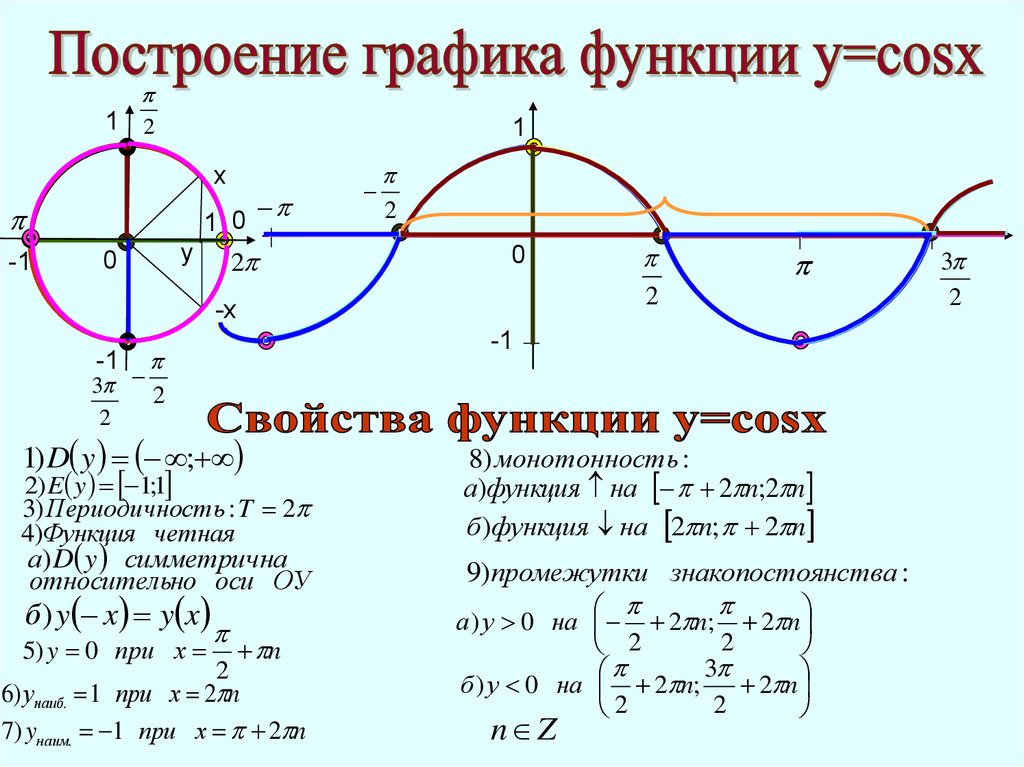
1) D y ;
2) E y 1;1
3) Периодичность : T 2
4)Функция четная
8) монотонность :
а)функция на 2 n;2 n
б )функция на 2 n; 2 n
б) y x y x
9)промежутки знакопостоянства :
а ) у 0 на 2 n; 2 n
а) D y симметрична
относительно оси ОУ
5) y 0 при х
n
2
6) унаиб. 1 при х 2 n
7) yнаим. 1 при х 2 n
2
2
3
б ) у 0 на 2 n;
2 n
2
2
n Z
3
2

7.

tgx
1 2
x у
1 0
2
-1
0
-х -у
-1
3
2
1
2
0
2
3
2
-1
2
1) D y : х n
2
2) E y ;
3) Периодичность : T
4)Функция нечетная.
5) Нули функции :
y 0 при х n
8) монотонность :
а)функция на n; n
2
2
9)промежутки знакопостоянства :
б ) у 0 на n; n
2
а) у 0 на n; n
2
n Z

8.

-y
y
1 2
1
x
1 0 2
-1
0
2
-х
-1
0
2
3
2
2
-1
3 2
2
1) D y : х n
2) E y ;
3) Периодичность : T
4)Функция нечетная
5) Нули функции :
y 0прих n
8) монотонность :
а)функция на n; n
9)промежутки знакопостоянства
б ) у 0на n; n
2
а) у 0на n; n
2
n Z

9.

1
2
arcsin a
a
arccos a
arccos a
arccos a
a
-1
arcsin a x, sin x a
x
x
-1 a
a 1;1
arcsin a arcsin a
2
tgx a
a 1;1
a
arccos a 0;
a ctgx
arcctg a
arccos a
arctga x, tgx a
arctg a
arctg a arctga
a 1
arccos a arccos a
arctga
arccos a x, cos x a
;
2 2
2
x
x
0
arcsin a arcsin a
2
x
arcctga
x
0
a R
arctga ;
2 2
a
arcctg a arcctga
arcctga x, ctgx a
a R
arcctga 0;

10.

2
3
1 2
3
1 2
0
2
3
0
1
2
1
2
-1
1
-1 3
2
2
3
1
2
2
3
Частные случаи:
1) cos x 0
x
x
2
n
2) cos x 1
х 2 n
3) cos x 1
x 2 n
1
2
2 n
3
x 2 n
3
1
2
2
x
2 n
3
2
x
2 n
3
cos x
8
3
2
4
3
3 2
-1
3
1
cos x
2
0
2
3
3 5
2 3
7 5
3 2
cos x a, где 1 a 1
x arccos a 2 n, n Z
x arccos
x
3
1
2 n;
2
2 n
1
x arccos n;
2
1
x arccos 2 n;
2
x
2
2 n
3

11.

1 2
5
6
1
2
6
1
0
0
-1
7
6
Частные случаи:
1) sin x 0
х n
2) sin x 1
2
2
2 n
3) sin x 1
x 2 n
2
7
6
6
0
6
1
2
2
x
1 2
-1 3
2
5
6
-1
2 n
6
5
x
2 n
6
sin x
x
x
6
1
2
2 n
7
2 n
6
13
6
5
2
17
6
3
sin x a, где 1 a 1
1
sin x
2
x
2
3
2
x 1 arcsin a n, n Z
n
x 1 arcsin
n
x 1n n
6
1
n;
2
1
n
x 1 arcsin n;
2
x 1
n 1
6
n

12.

1 2
0
-1
3
2
x а
1
1 0
2
-1
tgx
arctga
2
-х -а
0
arctga
2
3
2
-1
2
arctg a arctga
tgx a, а ;
х
2
n
tgx a, а ;
х
2
n
х arctga n
х arctga n,
tgx 0
х n
1
ctgx a tgx
a
n Z

13.

5
6
6
1
2
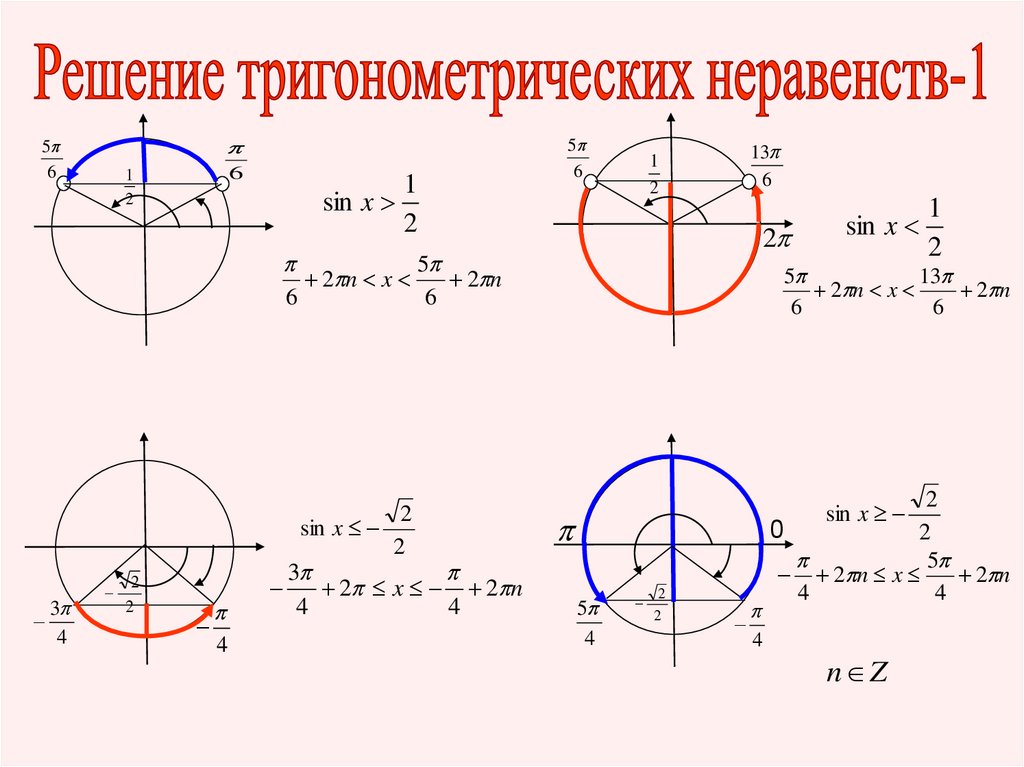
sin x
6
3
4
2
2
4
1
2
2 n x
5
6
13
6
1
2
2
5
2 n
6
2
sin x
2
3
2 x 2 n
4
4
sin x
1
2
5
13
2 n x
2 n
6
6
2
0
2
5
2 n x
2 n
4
4
sin x
5
4
2
2
4
n Z

14.

6
3
2
6
3
cos x
2
2 n x
6
2 n
6
3
2
11
6
6
3
4
3
4
2
2
cos x
5
4
3
2
11
2 n x
2 n
6
6
cos x
2
2
3
5
2 n x
2 n
4
4
2
2
cos x
3
4
2
2
3
3
2 n x
2 n
4
4
n Z

15.

2
tgx
2
6
3
3
6
5
6
3
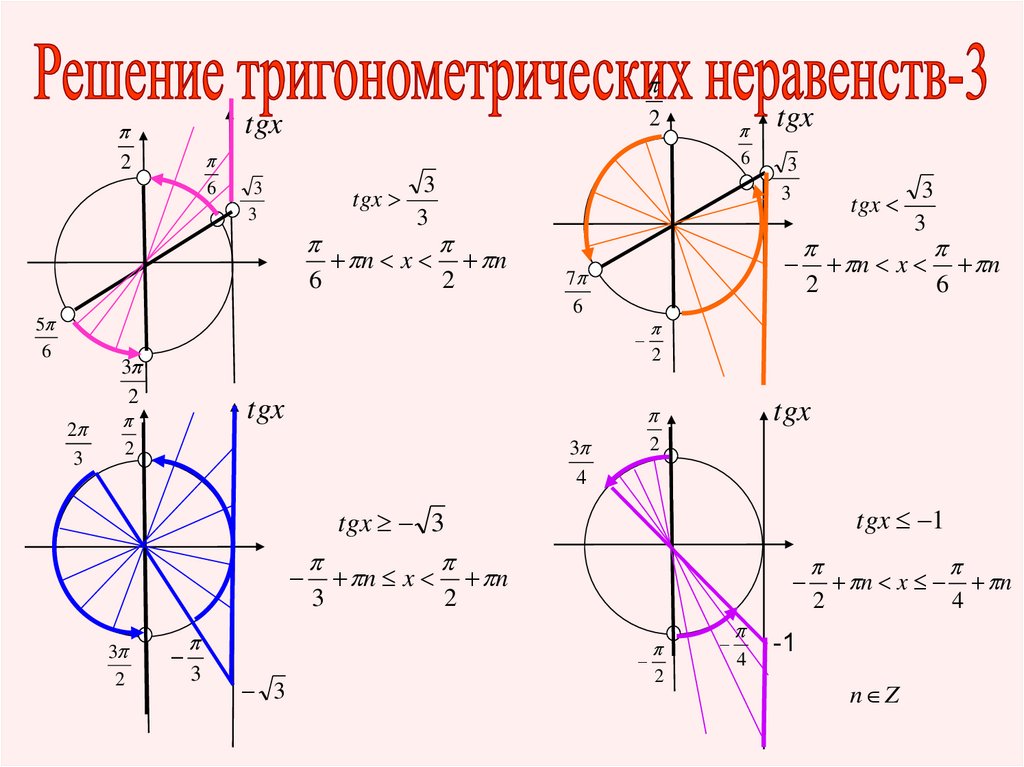
tgx
3
n x
2
n
2
3
7
6
tgx
3
4
2
3
2
3
tgx
2
3
3
n x
6
n
2
tgx
2
tgx 1
2
3
3
3
tgx 3
n x n
3
tgx
3
2
6
2
4
2
n x
-1
n Z
4
n

16.

4
ctgx
1
0
1
5
4
ctgx 1
n x
4
n
3
ctgx 1
2
5
4
ctgx
3
3 2
4
ctgx
4
3
2
3
3
ctgx
0
2
5
3
ctgx
3
3
2
n x n
3
n x n
ctgx
n x
5
3
3
3
2
n
3
n Z