Similar presentations:
Графики и свойства тригонометрических функций
1.
2.
Свойства и график функции y=tgx и y=ctg xПеречень вопросов, рассматриваемых в
Глоссарий по теме
теме
Асимптотой кривой называется прямая,
Изучение и объяснение свойств функций
расстояние до которой от точки, лежащей
y=tgx и y=ctgx с помощью графика;
на кривой, стремится к нулю при
Определение свойств и положения графика
неограниченном удалении от начала
тригонометрических функций вида
координат этой точки по кривой.
y=|tg(k|x|+b)| y=|ctg(k|x|+b|;
Тангенсоида –
Объяснение зависимости свойств и
график функции у = tgx; плоская кривая, изо
положения графика функции вида
бражающая
y=|tg(k|x|+b)| и y=|ctg(k|x|+b| от
изменение тангенса в зависимости от изме
значения коэффициентов k,b.
нения его аргумента (угла).
3.
Теоретический материал для самостоятельного изученияАктуализация знаний
Вычислите:
4.
5.
6.
7.
8.
9.
10.
11.
12.
Исследование функций.Перечень вопросов, рассматриваемых в
теме:
функция, аргумент функции, значение
функции
график функции, преобразование графика
функции
свойства функции, исследование свойств
функции
Глоссарий по теме урока
Определение
Зависимость переменной у от переменной
х называется функцией, если каждому
значению х соответствует единственное
значение у.
х – независимая переменная, аргумент,
у - зависимая переменная, значение
функции
Определение
Множество значений аргумента функции
называется областью определения функции
и обозначается D(y).
13.
ОпределениеМножество значений, которые принимает
сама функция, называется множеством
значений функции и обозначается Е(у).
Определение
Функция у = f(х) называется четной, если
она обладает двумя свойствами:
область определения этой функции
симметрична относительно 0;
для любого х из области определения
выполняется равенство f(-х)=f(х).
Функция у = f(х) называется нечетной, если
она обладает двумя свойствами:
область определения этой функции
симметрична относительно 0;
для любого х из области определения
выполняется равенство f(-х)=-f(х).
Определение
Значения аргумента, при которых значение
функции равно 0, называются корнями
(нулями) функции.
14.
ОпределениеФункция у=f(x) возрастает на промежутке
(а; в), если для любых х1, х2 из этого
промежутка, таких, что х1<х2, выполняется
неравенство у1<у2.
Функция у=f(x) убывает на промежутке (а;
в), если для любых х1, х2 из этого
промежутка, таких что, х1<х2, выполняется
неравенство у1>у2.























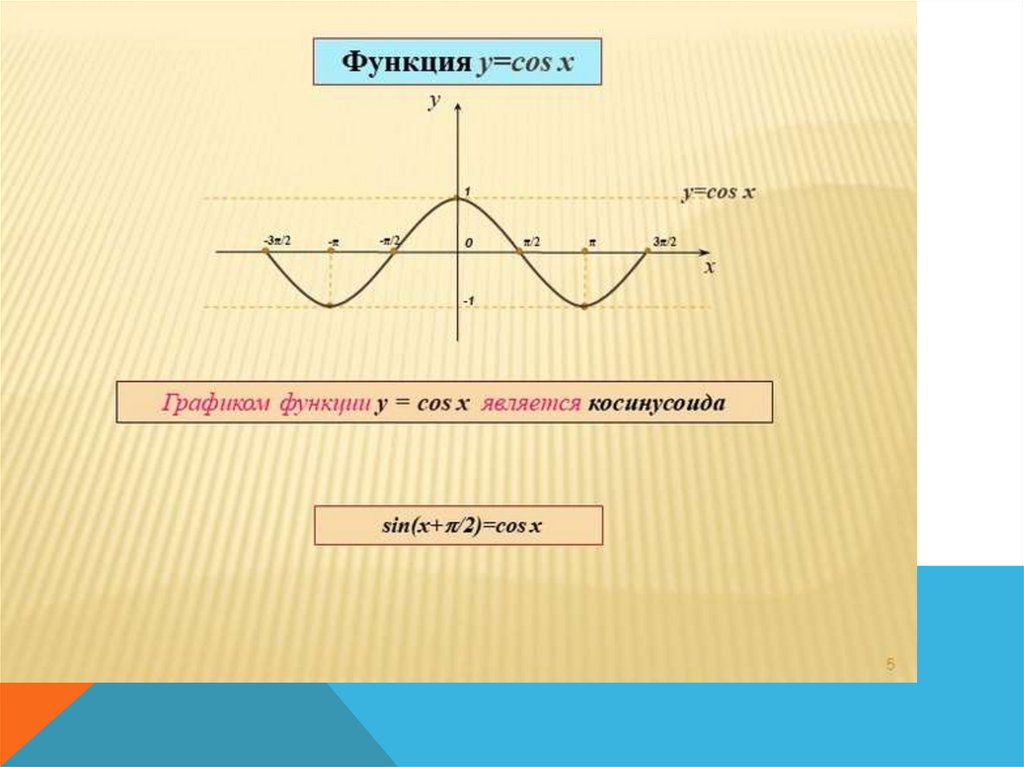






 mathematics
mathematics








