Similar presentations:
Аналитическая геометрия. Глава III
1. Глава III. Аналитическая геометрия
Аналитическая геометрия – раздел геометрии, в которомпростейшие линии и поверхности (прямые, плоскости,
кривые и поверхности второго порядка) исследуются
средствами алгебры.
Линией на плоскости называют геометрическое место точек
M(x;y), координаты которых удовлетворяют уравнению
F(x,y) = 0,
где F(x,y) – многочлен степени n.
пропустить 10 клеточек
2.
Уравнения прямой на плоскостиНазвание
общее уравнение
прямой
Уравнение
Ax + By + C = 0
уравнение прямой в
координатной форме
уравнением прямой в
отрезках
…
параметрические
уравнения прямой
каноническое уравнение
прямой
уравнение прямой,
проходящей через две
точки
уравнение прямой с
угловым
коэффициентом
ЗАПОЛНИТЬ!
Параметры
N={A;B} – вектор
нормали
3. Прямая на плоскости
ЗАДАЧА 1. Записать уравнение прямой, проходящей через точкуM0(x0;y0), перпендикулярно вектору N̄ = {A; B}.
Пусть M(x;y) – произвольная точка на прямой (текущая точка),
r̄ – радиус-вектор точки M ,
r̄0 – радиус-вектор точки
M0 .
y
M0(x0; y0)
M(x; y)
l
O
пропустить 12 клеточек
x
4. ВИДЫ УРАВНЕНИЯ ПРЯМОЙ
Если в уравнении Ax+By+C = 0 все коэффициенты A,B и Cотличны от нуля, то уравнение называют полным; если хотя
бы один из коэффициентов равен нулю – уравнение называют
неполным.
1) Пусть общее уравнение прямой – полное.
Получение уравнения:
y
B(0; b)
пропустить 12 клеточек
A(a; 0)
Смысл a и b –
Уравнение (3) называют уравнением прямой в отрезках.
x
5.
2) Дано Ax+By+C = 0 общее уравнение прямой.A≠0 B ≠0 C = 0, т.е.
Ax+By = 0.
Такая прямая проходит через начало координат O(0;0).
y
O(0; 0)
x
6.
3) Дано Ax+By+C = 0 общее уравнение прямой.A=0 или B =0, а C 0
ИЛИ
и
x=a
y=b.
y
y
B(0; b)
A(a; 0)
x
x
Таким образом, прямая в уравнении которой отсутствует одна
из координат, параллельна оси отсутствующей координаты
7.
4) Дано Ax+By+C = 0 общее уравнение прямой.C = 0 A = 0 или B = 0, т.е. уравнение прямой:
Ax = 0 или By = 0.
Или
x = 0 (уравнения оси Oy)
y = 0 (уравнения оси Ox).
8.
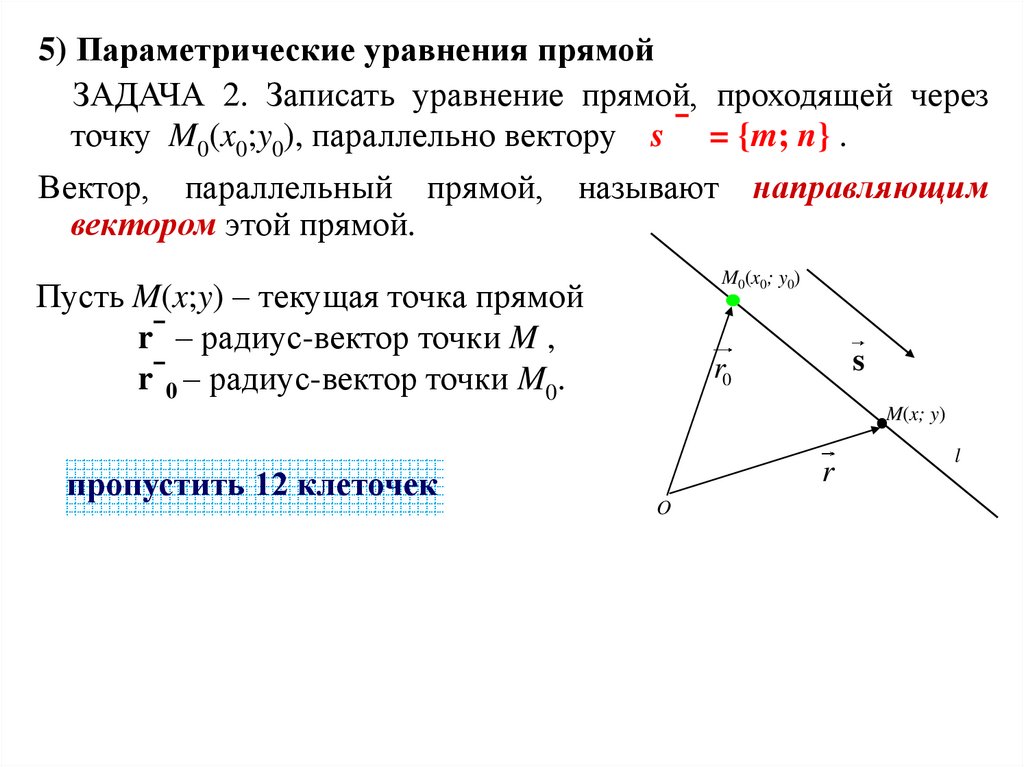
5) Параметрические уравнения прямойЗАДАЧА 2. Записать уравнение прямой, проходящей через
точку M0(x0;y0), параллельно вектору s ̄ = {m; n} .
Вектор, параллельный прямой, называют направляющим
вектором этой прямой.
M0(x0; y0)
Пусть M(x;y) – текущая точка прямой
r̄ – радиус-вектор точки M ,
r̄0 – радиус-вектор точки M0.
s
r0
M(x; y)
пропустить 12 клеточек
r
O
l
9.
6) Каноническое уравнение прямой на плоскостипропустить 10 клеточек
7) Уравнение прямой, проходящей через две точки.
Пусть прямая проходит через две точки M1(x1,y1) и M2(x2,y2) .
M1
M2
пропустить 10 клеточек
10.
8) Уравнение прямой с угловым коэффициентомПусть прямая l задана
x x0 y y0
m
n
пропустить 12 клеточек
11. Взаимное расположение прямых на плоскости
На плоскости две прямые могут:а) быть параллельны,
б) пересекаться.
Рассмотрим 2 прямые:
ℓ1: A1x + B1y + C1 = 0 или y = k1x + b1
ℓ2: A2x + B2y + C2 = 0 или y = k2x + b2
N1 { A1; B1}
N 2 { A2 ; B2 }
1) Пусть прямые параллельны:
(не совпадают):
A1
B1
C1
или k1 = k2 ; b1 ≠ b2
A2 B 2 C 2
Место для
рисунка
(совпадают): A1 B1 C 1
или k1 = k2 ; b1 = b2
A2 B 2 C 2










 mathematics
mathematics








