Similar presentations:
Основы аналитической геометрии
1. Лекция 10 Основы аналитической геометрии (I)
2. Аналитическая геометрия (Analytic geometry)
Аналитическая геометрия - раздел геометрии, вкотором геометрические фигуры и их свойства
исследуются средствами алгебры.
Опр. Линией на плоскости (line in the plane) в
выбранной CК называют геометрическое место
точек
M(x;y),
координаты
которых
удовлетворяют уравнению
F(x,y) = 0,
где F(x,y) – некая функция.
Если F(x,y) – многочлен степени n, то линия
называется алгебраической.
3.
Поверхностью (surface) в выбранной СКназывают геометрическое место точек M(x;y;z),
координаты которых удовлетворяют уравнению
F(x,y,z) = 0.
П. Уравнение x2+y2-1=0 определяет на плоскости
окружность радиуса R=1 с центром в точке
O(0,0).
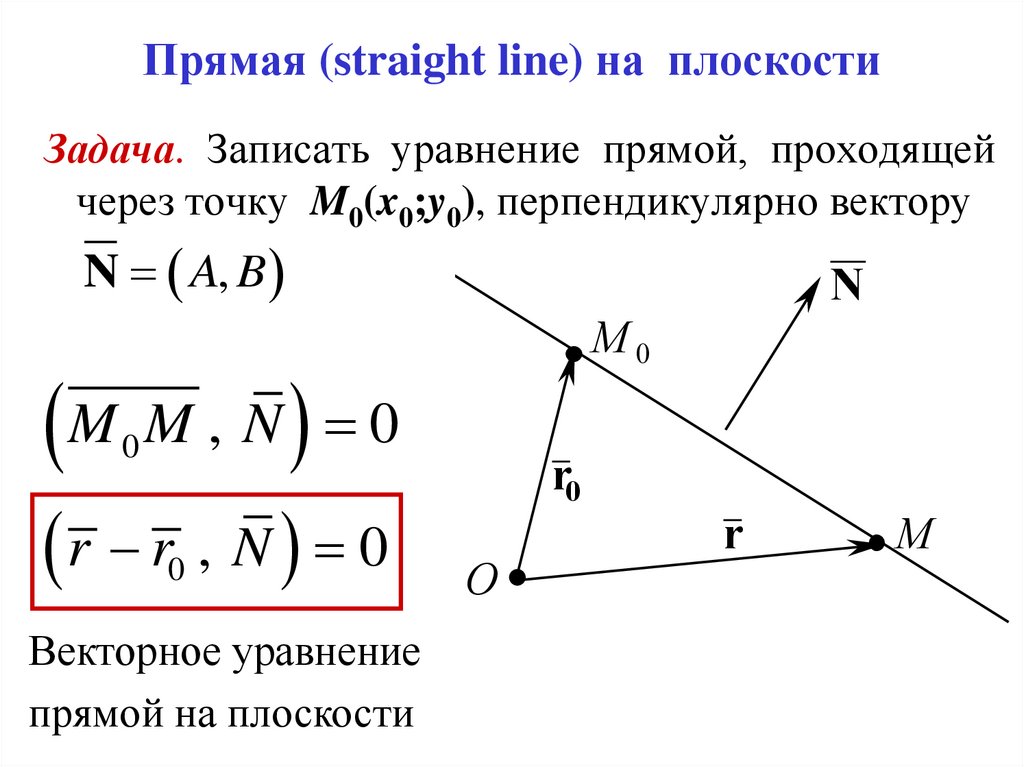
4. Прямая (straight line) на плоскости
Задача. Записать уравнение прямой, проходящейчерез точку M0(x0;y0), перпендикулярно вектору
N A, B
N
M0
M M , N 0
0
r r0 , N 0
Векторное уравнение
прямой на плоскости
r0
O
r
M
5.
r r , N 00
A( x x0 ) B( y y0 ) 0;
Ax By Ax0 By0 0;
Ax By C 0
где
A B 0,
2
2
называется общим уравнением (general equation)
прямой на плоскости.
6. Исследование общего уравнения прямой
Т. В общей ДСК на плоскости каждая прямаяможет быть задана линейным уравнением.
Обратно, каждое линейное уравнение в общей
ДСК на плоскости определяет прямую.
Исследование общего уравнения прямой
1. Рассмотрим полное уравнение
Ax By C 0
A 0, B 0, C 0
A
B
x
y 1
Ax By C
C
C
7.
xy
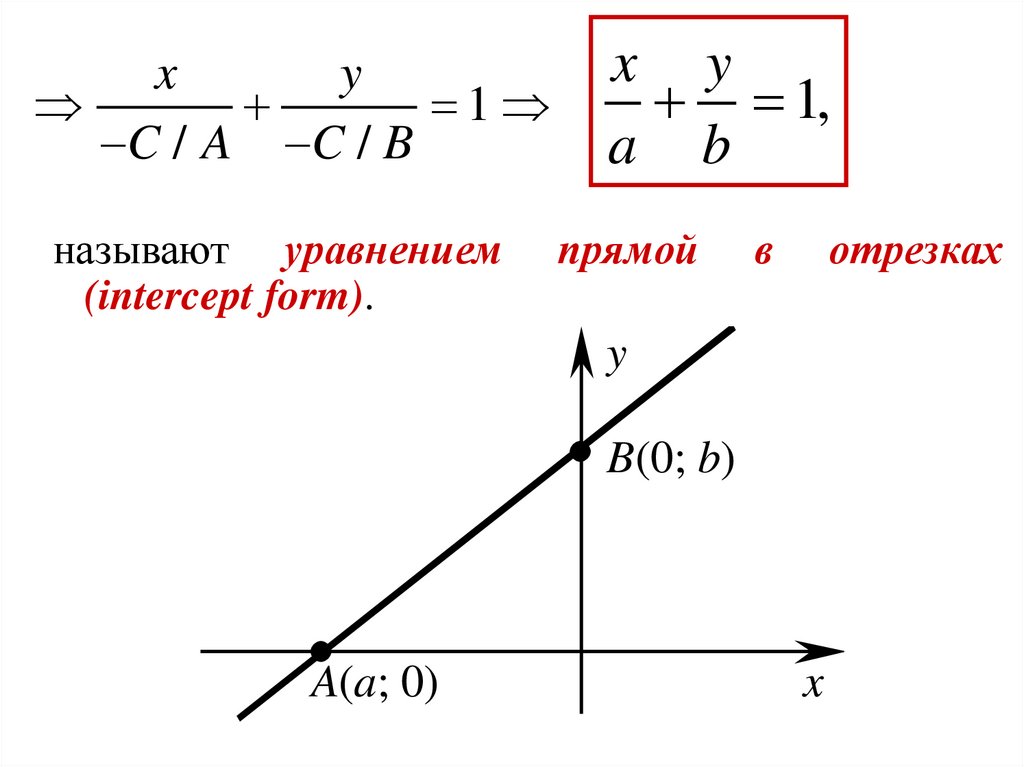
1
C / A C / B
называют уравнением
(intercept form).
x y
1,
a b
прямой
в
отрезках
y
B(0; b)
A(a; 0)
x
8.
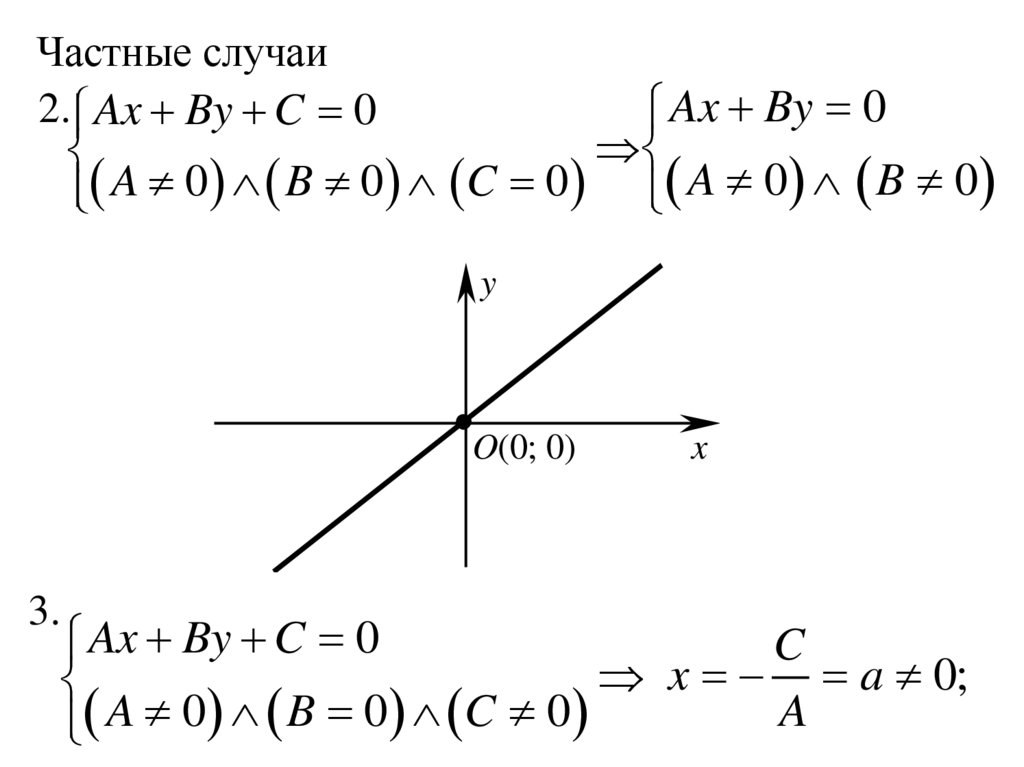
Частные случаи2.
Ax By C 0
Ax By 0
A 0 B 0
A 0 B 0 C 0
y
O(0; 0)
3.
x
C
Ax By C 0
x a 0;
A
A 0 B 0 C 0
9.
Ax By C 0A 0 B 0 C 0
C
y b 0;
B
y
y
B(0; b)
A(a; 0)
x
x
4. Ax By C 0
A 0 B 0 C 0
y 0 (ось ОХ );
Ax By C 0
x 0 (ось ОY ).
A 0 B 0 C 0
10.
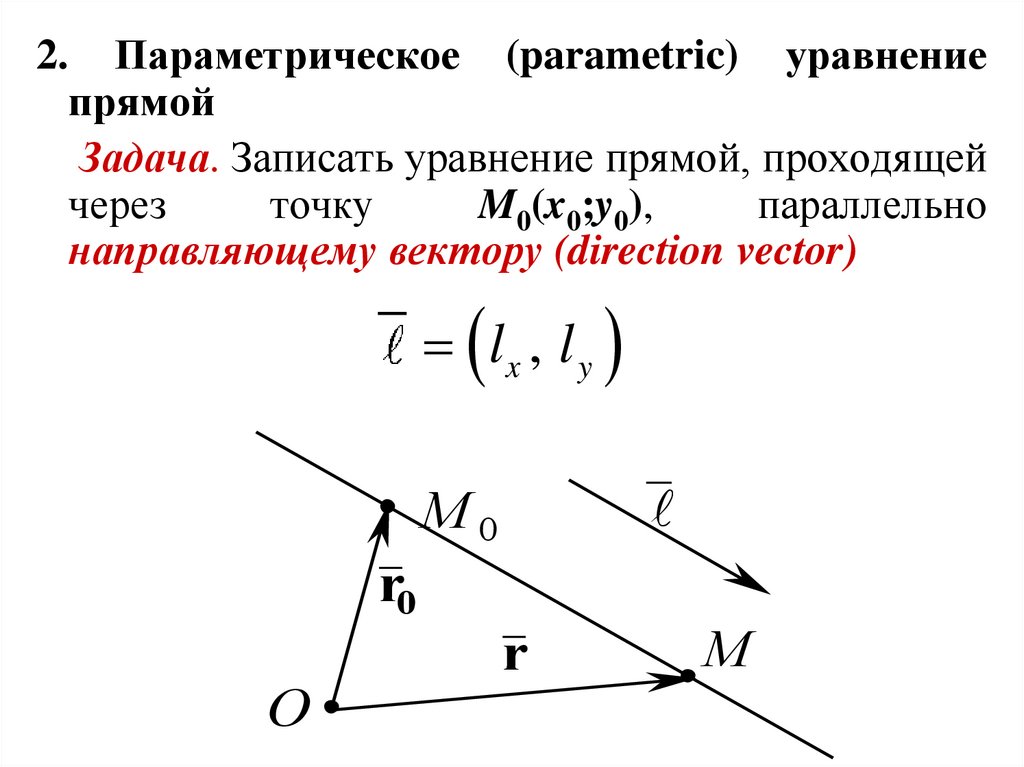
2. Параметрическое (parametric) уравнениепрямой
Задача. Записать уравнение прямой, проходящей
через
точку
M0(x0;y0),
параллельно
направляющему вектору (direction vector)
lx , l y
M0
r0
O
r
M
11.
r r0 tl , tr r0 tl , t
x x0 lx
t
y y0 l y
x x0 tlx
, t .
y
y
tl
0
y
12.
3. Каноническое (standard) уравнение прямой наплоскости
x x0 y y0
ly
lx
4. Уравнение прямой, проходящей через 2 точки
M1(x1,y1) и M2(x2,y2) (two point form)
l lx , l y x2 x1 , y2 y1
x x1
y y1
x2 x1 y2 y1
M1
M2
13.
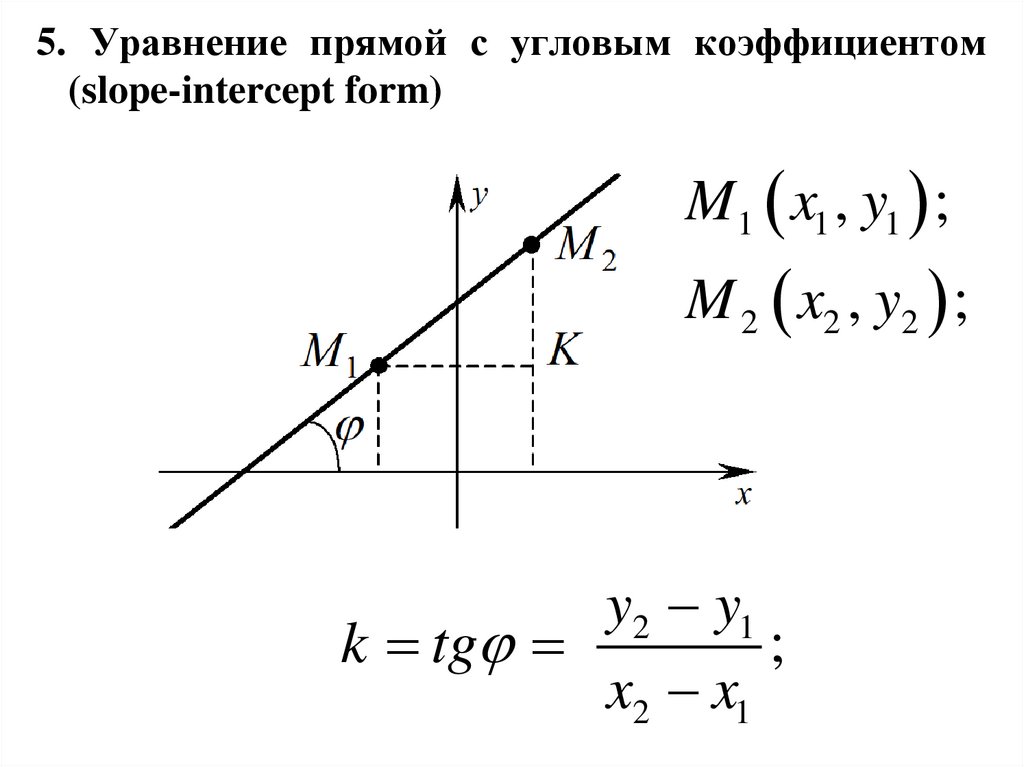
5. Уравнение прямой с угловым коэффициентом(slope-intercept form)
M1 x1 , y1 ;
M 2 x2 , y2 ;
y2 y1
;
k tg
x2 x1
14.
y2 y1y
y
x
x
1
1
x2 x1
k tg y2 y1
x2 x1
y y1 k x x1
y kx y1 kx1
y kx b
15.
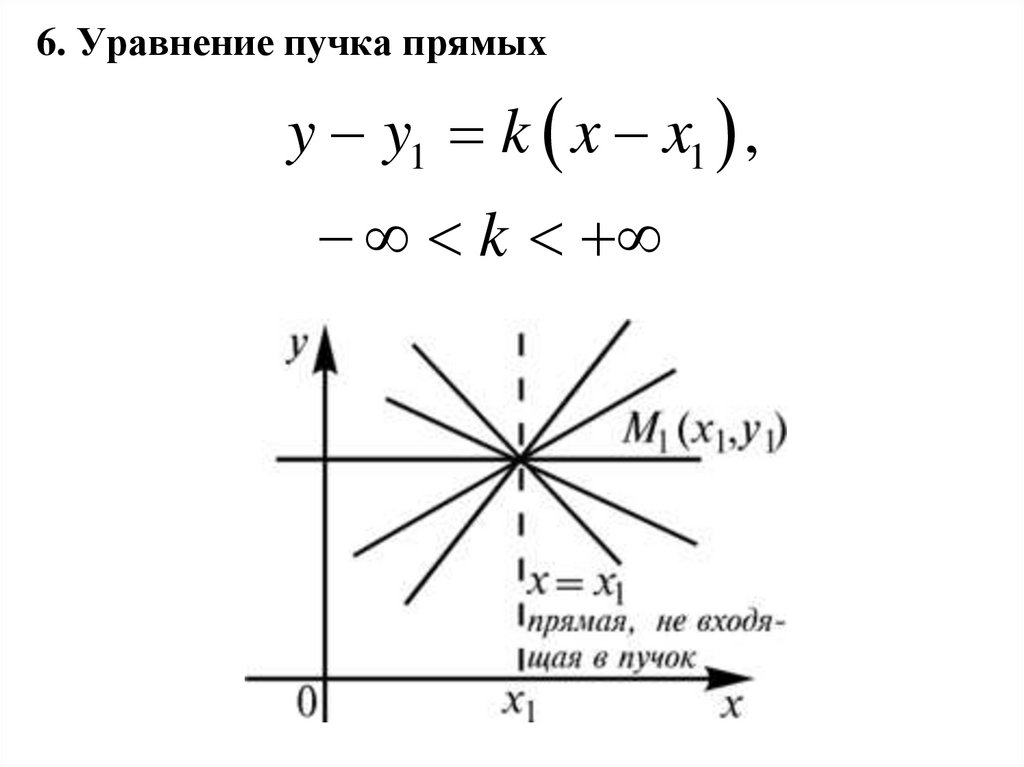
6. Уравнение пучка прямыхy y1 k x x1 ,
k
16. Взаимное расположение прямых на плоскости
На плоскости две прямые могут:а) совпадать,
б) быть параллельными,
в) пересекаться.
l1: A1x + B1y + C1 = 0 или y = k1x + b1
l2: A2x + B2y + C2 = 0 или y = k2x + b2
A1 B1 C1
l1 совпадает с l2 .
A
B
C
2
2
2
17.
N1N2
1
1
2
2
x
1
2
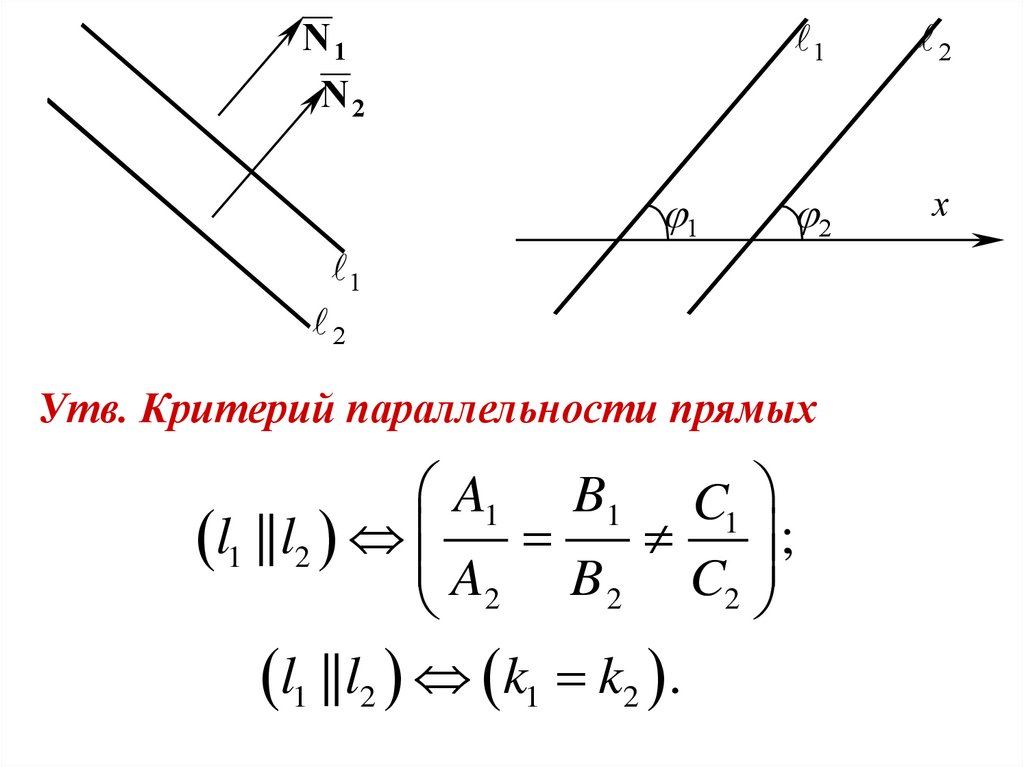
Утв. Критерий параллельности прямых
A1 B1 C1
l1 || l2 ;
A
B
C
2
2
2
l1 || l2 k1 k2 .
18.
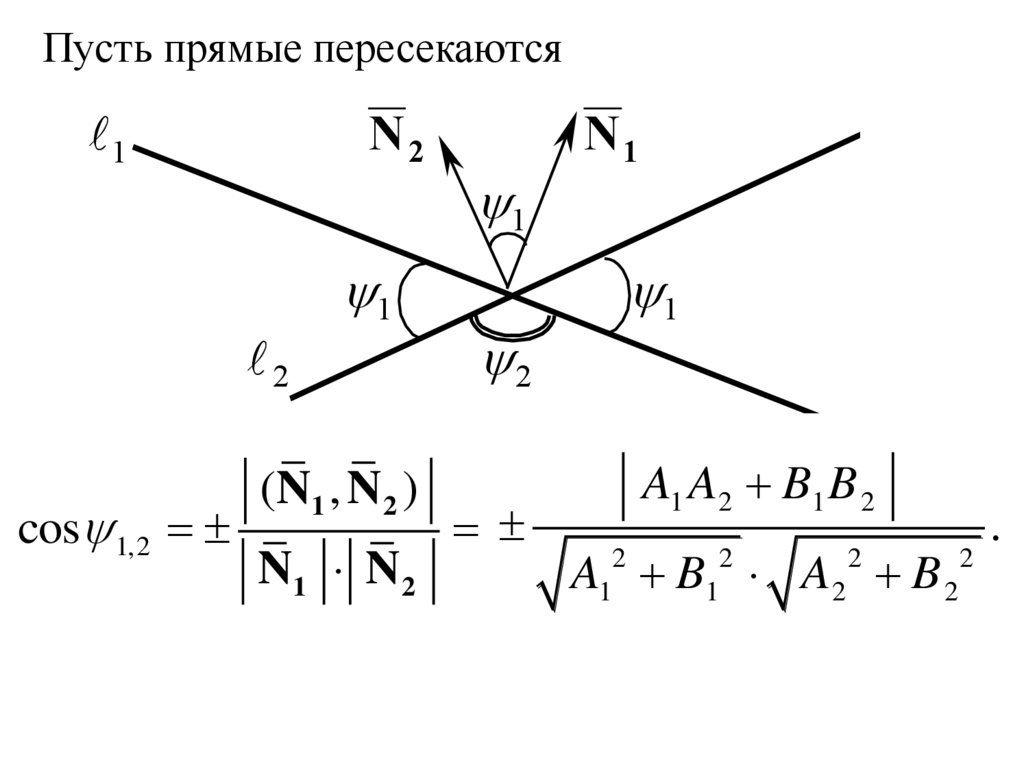
Пусть прямые пересекаютсяN2
1
1
2
cos 1,2
(N1 , N 2 )
N1 N 2
1
N1
1
2
A1 A2 B1 B 2
A B A2 B 2
2
1
2
1
2
2
.
19.
21
1
1
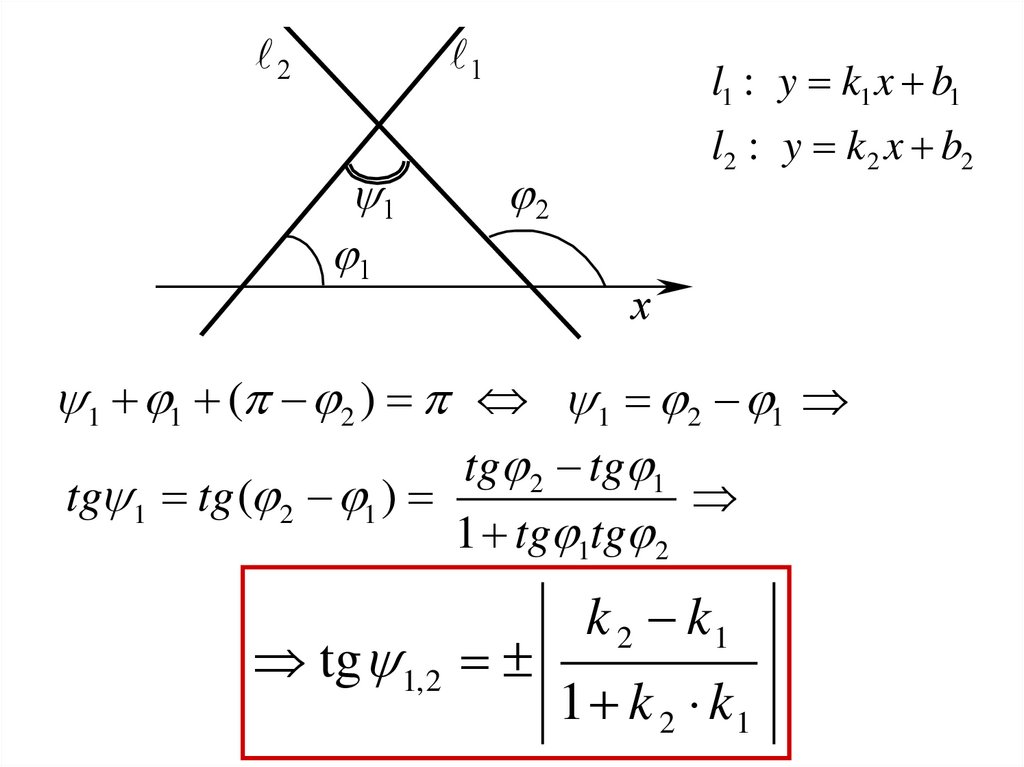
l1 : y k1 x b1
l2 : y k 2 x b2
2
x
1 1 ( 2 ) 1 2 1
tg 2 tg 1
tg 1 tg ( 2 1 )
1 tg 1tg 2
tg 1,2
k 2 k1
1 k 2 k1
20. Расстояние от точки до прямой
Утв. Критерий перпендикулярности прямыхl1 l2 ( N1 , N 2 ) A1 A2 B1 B 2 0 ;
l1 l2 k1 k2 1 .
Расстояние от точки до прямой
Задача. Пусть прямая ℓ задана общим уравнением
Ax + By + C = 0 , M0(x0;y0) – точка, не
принадлежащая прямой ℓ.
Найти расстояние от точки M0 до прямой ℓ.
21.
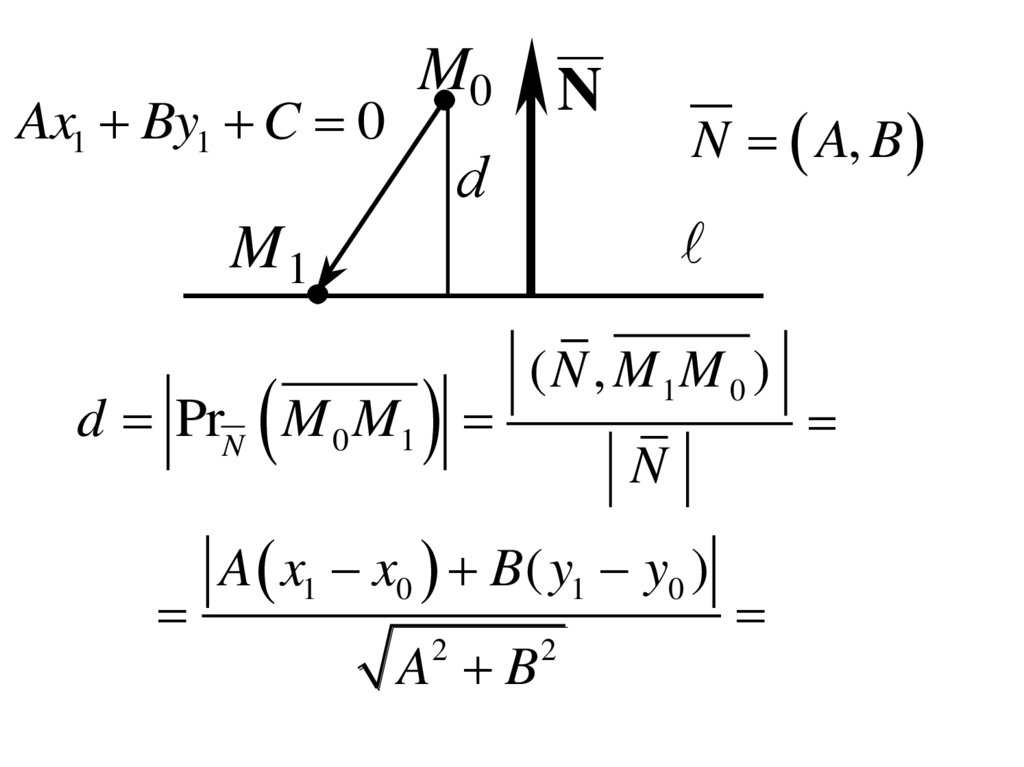
Ax1 By1 C 0M0
N
N A, B
d
M1
d PrN M 0 M1
( N , M 1M 0 )
N
A x1 x0 B( y1 y0 )
A B
2
2
22.
Ax1 By1 Ax0 By0A B
2
2
C Ax0 By0
A B
2
d
2
Ax0 By0 C
A B
2
2
.





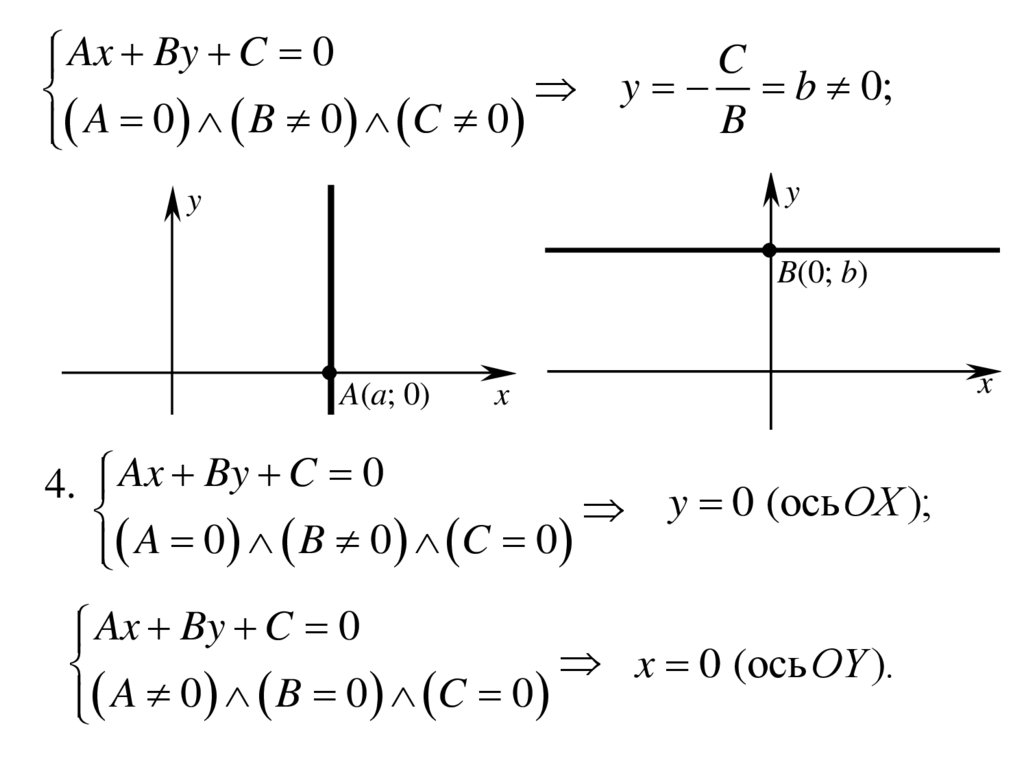
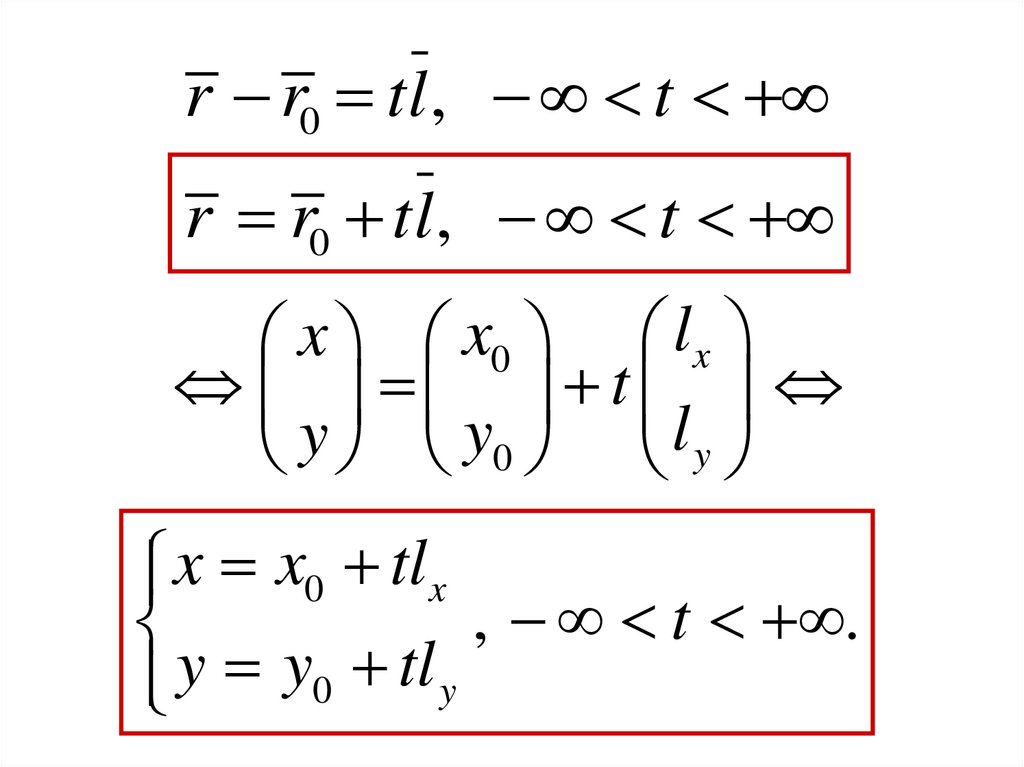

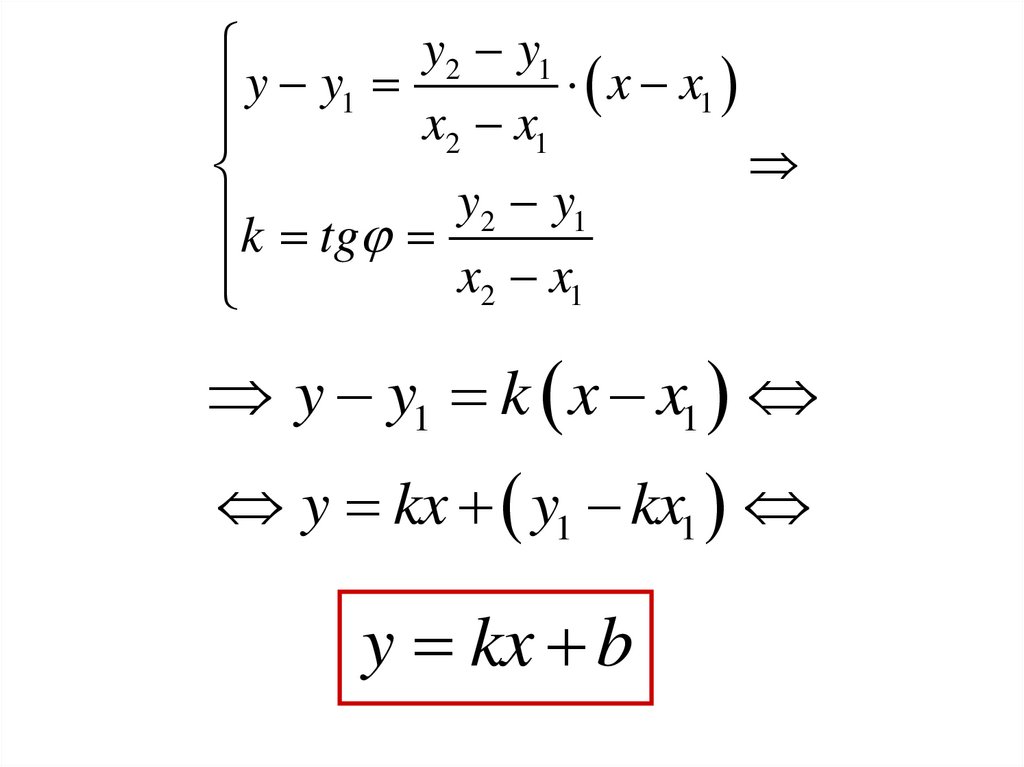



 mathematics
mathematics








