Основы аналитической геометрии

1. Основы аналитической геометрии

2. 1. Уравнение прямой на плоскости

1. УРАВНЕНИЕ ПРЯМОЙ НА
ПЛОСКОСТИ

3.

l
а
М0
r0
М
r
О
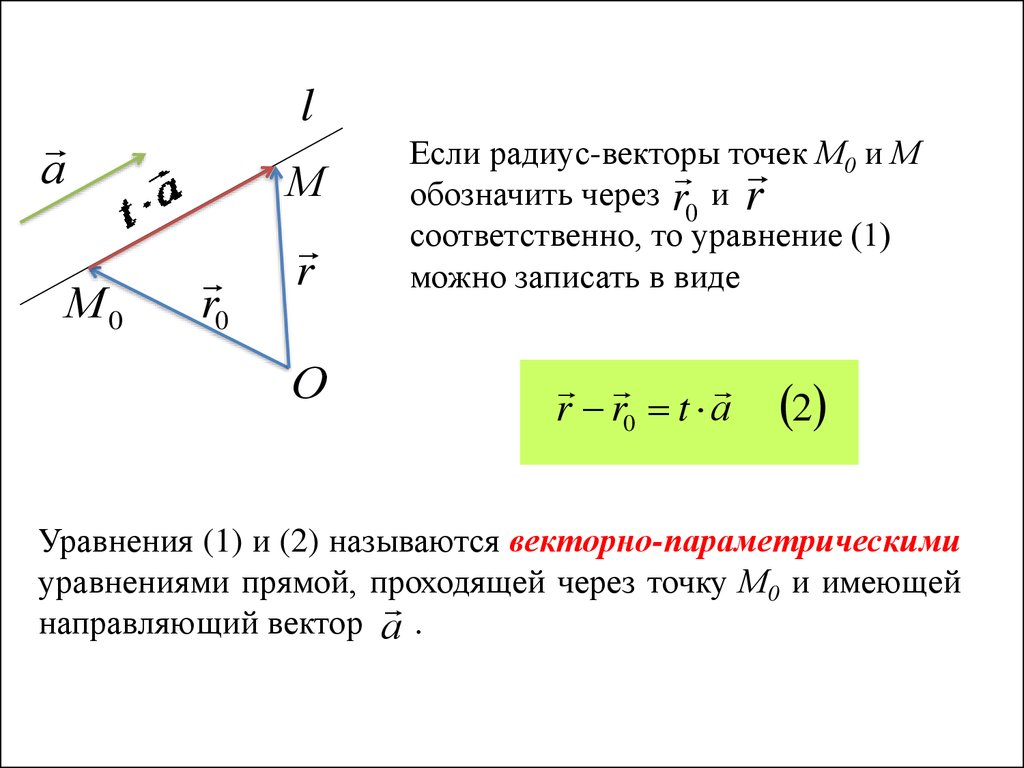
Если радиус-векторы точек
М0 и М
обозначить через r0 и r
соответственно, то уравнение (1)
можно записать в виде
r r0 t а
2
Уравнения (1) и (2) называются векторно-параметрическими
уравнениями прямой, проходящей через точку М0 и имеющей
направляющий вектор а .

4.

В координатной записи уравнение (1) имеет вид:
x x0 , y y0 ta1 , ta2
или
x x0 ta1 ,
y y0 ta2 .
(3)
Система уравнений (3) называется параметрическим
уравнением прямой, проходящей через точку М0(x0, y0) и
имеющей направляющий вектор а а1 , а2 .

5.

Параметрическое уравнение (3) равносильно уравнению, которое
называется каноническим уравнением прямой на плоскости.
x x0 y y0
a1
a2
4
Замечание: в каноническом уравнении (4) допускаются значения а1 = 0 или
а2=0. это не означает, что можно выполнить деление на 0. Из канонического
уравнения получаем информацию о том, что направляющий вектор прямой
имеет координаты, из которых одна нулевая. Причем в случает а1 = 0 уравнение
прямой имеет вид x - x0 = 0 или x = x0, а в случае а2 = 0 уравнение прямой имеет
вид y - y0 = 0 или y = y0.
y
y
x = x0
y = y0
y0
O
x0
x
O
x

6. Задача. Написать уравнение прямой, проходящей через две точки М0(x0, y0) и М1(x1, y1) .

а
М0(x0, y0)
М1(x1, y1)
Решение: вектор a M 0 M1 x1 x0 , y1 y0
является направляющим вектором прямой.
Значит, прямая, проходящая через
заданные две точки М0(x0, y0) и М1(x1, y1) это та же прямая, которая проходит через
точку М0(x0, y0) и имеет направляющий
вектор a M 0 M1 x1 x0 , y1 y0 .
Уравнение этой прямой по формуле (4) имеет вид:
x x0
y y0
x1 x0 y1 y0
5
Уравнение (5) и есть уравнение прямой, проходящей через две
точки М0(x0, y0) и М1(x1, y1).

7.

Теорема. Всякая прямая на плоскости задается некоторым
уравнение первого порядка от двух переменных x и y
Ax By C 0
(6)
и, наоборот, любое такое уравнение является уравнением
некоторой прямой на плоскости.
Уравнение (6) называется общим уравнением прямой на
плоскости.
a B, A
Замечание: Вектор
является направляющим
вектором прямой, заданной общим уравнением.

8.

Замечание.
Пусть в общем уравнении прямой (6) коэффициент В≠0.
Тогда уравнение (6) можно представить в виде
или
A
C
y
Где
B
x
y kx b
(7)
B
A
C
k , b
B
B
Число k называется угловым коэффициентом прямой, а
уравнение (7) – уравнением прямой с угловым
коэффициентом.
Т.о. любая прямая, не параллельная оси Оy (В≠0), может быть
задана уравнением с угловым коэффициентом.

9.

Замечание.
Угловой коэффициент k прямой
определяется однозначно и
равняется тангенсу угла
наклона прямой к оси Ox:
y
А
α
k tg
α
O
-В
x
(8)

10. 2. Нормальный вектор прямой. Расстояние от точки до прямой

2. НОРМАЛЬНЫЙ ВЕКТОР
ПРЯМОЙ. РАССТОЯНИЕ ОТ
ТОЧКИ ДО ПРЯМОЙ

11.

Опр. Если вектор n перпендикулярен
направляющему вектору а прямой l, то он
называется нормальным вектором прямой l.
y
а
n
l
O
x

12.

Теорема. Пусть прямая задана общим
уравнением:
Ax By C 0
(6)
Тогда вектор n
А, В является
нормальным вектором этой прямой.

13.

Задача. Найти уравнение прямой l, которая проходит через
точку М0(x0, y0) и имеет нормальный вектор n А, В .
Решение:
Возьмем на прямой l произвольную точку М(x, y) и
рассмотрим вектор M 0 M x x0 , y y0 .
y
M
M
и
n
Т.к. векторы 0
перпендикулярны,
n
то их скалярное произведение равно нулю:
М(x, y)
M 0 M n 0 , т.е.
А x x0 ) В( y y0 0
М0(x0, y0)
(8)
O
Уравнение (8) называется уравнением прямой, проходящей
через точку М0(x0, y0) перпендикулярно вектору n А, В .
x

14.

Теорема. Расстояние d от точки М0(x0, y0) до прямой,
заданной общим уравнением
Ax By C 0
(6)
вычисляется формулой
d
Ax0 By 0 C
A2 B 2
(9)

15.

Задача. Найти расстояние от точки М0(1, 5) до
прямой, заданной общим уравнением 3x – 4y – 3 = 0.
Решение:
По формуле (9) имеем
d
Ax0 By 0 C
A2 B 2
3 1 4 5 3
32 42
4

16. 3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

3. УГОЛ МЕЖДУ ДВУМЯ
ПРЯМЫМИ. УСЛОВИЕ
ПАРАЛЛЕЛЬНОСТИ И
ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ
ПРЯМЫХ

17.

Пусть l1 и l2 – две произвольные прямые на
плоскости.
Опр. Углом между двумя прямыми l1 и l2 на
плоскости называется угол между их
направляющими векторами.
b
b
а
l1

18.

Пусть l1 и l2 заданы общими уравнениями:
A1 x B1 y C1 0
A2 x B2 y C2 0
a B1 , A1 и b B2 , A2 - направляющие векторы.
Тогда косинус угла между прямыми вычисляется по
формуле:
cos
A1 A2 B1 B2
A12 B12 A22 B22
(10)

19.

условие перпендикулярности прямых: прямые l1 и l2
перпендикулярны, если нормальные векторы
n1 A1 , B1 и n2 A2 , B2 ортогональны, т.е.
n1 n2 A1 A2 B1B2 0
условие параллельности прямых: прямые l1 и l2
параллельны, если их направляющие векторы
a B1 , A1 и b B2 , A2 коллинеарны, т.е.
координаты этих векторов пропорциональны
А1 В1
А2 В2

20.

если прямые l1 и l2 - не параллельны оси Oy и заданы уравнениями с
угловым коэффициентом (7):
y k x b
1
1
y k2 x b2
Тогда угол между двумя прямыми определяется формулой:
k 2 k1
tg
1 k1k 2
(11)
Две прямые параллельны тогда и только тогда, когда тангенс угла
между ними равен нулю: tgφ=0, т.е. выполняется равенство k1 = k2.
Прямые l1 и l2 перпендикулярны тогда и только тогда, когда φ=π/2,
а значит, котангенс угла между ними равен нулю:
ctg
1 k1k 2
0
k 2 k1
Отсюда получаем условие перпендикулярности прямых:
k1 k 2 -1 или k 2
1
k1