триг теңсіздік 7 каз

1.

Қарапайым
тригонометриялық
теңсіздіктерді шешу

2.

I. Қарапайым тригонометриялық
теңсіздіктерді шешу.
Белгісізі тригонометриялық функцияның
аргументі түрінде берілген теңсіздікті
тригонометриалық теңсіздік деп атайды

3.

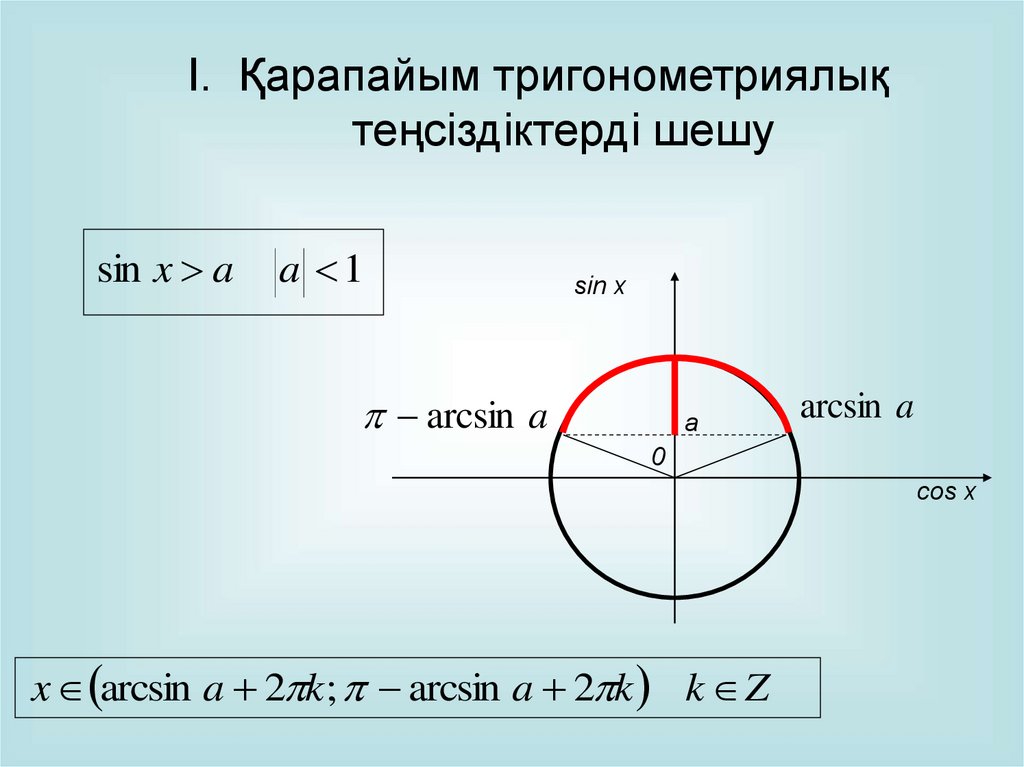
I. Қарапайым тригонометриялық
теңсіздіктерді шешу
sin x a
a 1
sin x
arcsin a
a
arcsin a
0
cos x
x arcsin a 2 k; arcsin a 2 k k Z

4.

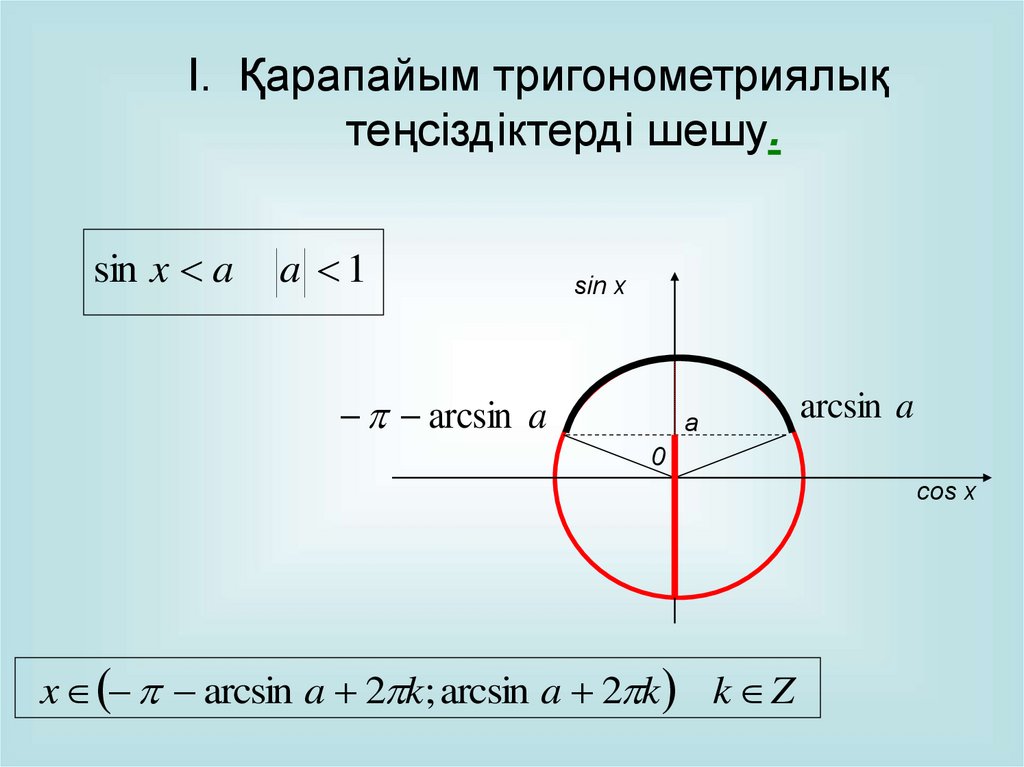
I. Қарапайым тригонометриялық
теңсіздіктерді шешу.
sin x a
a 1
sin x
arcsin a
a
arcsin a
0
cos x
x arcsin a 2 k; arcsin a 2 k k Z

5.

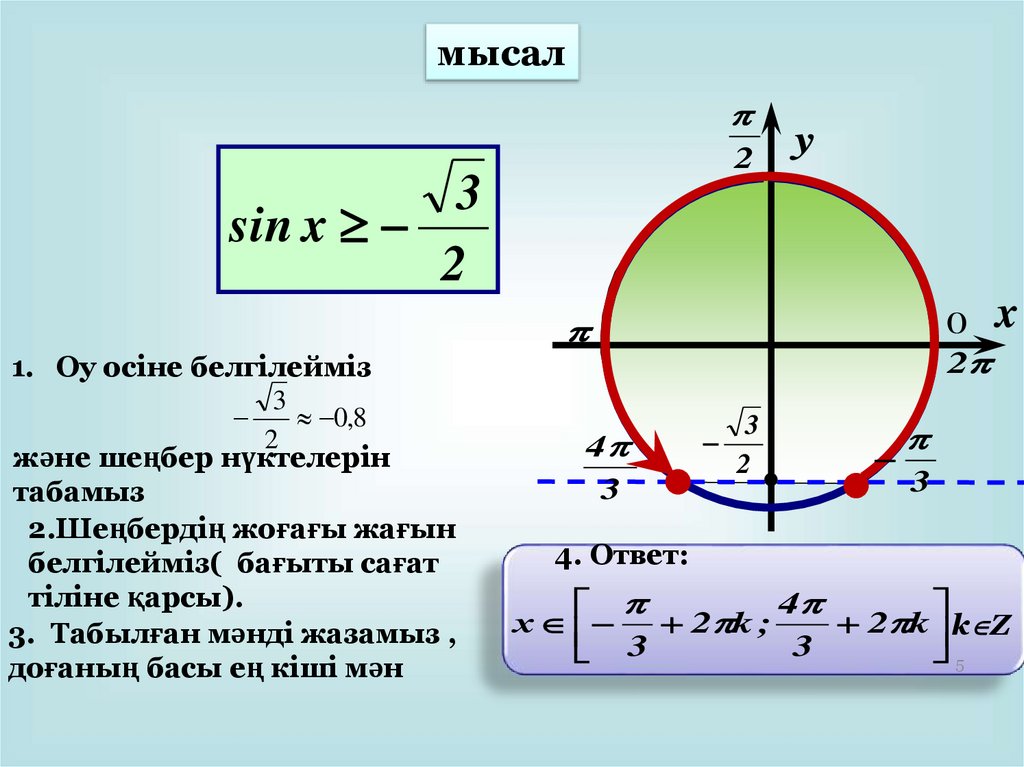
мысал
2
3
sin x
2
y
0 x
2
1. Оу осіне белгілейміз
3
0,8
2
және шеңбер нүктелерін
табамыз
2.Шеңбердің жоғағы жағын
белгілейміз( бағыты сағат
тіліне қарсы).
3. Табылған мәнді жазамыз ,
доғаның басы ең кіші мән
4
3
3
2
3
4. Ответ:
4
х
2 k ;
2 k k Z
3
3
5

6.

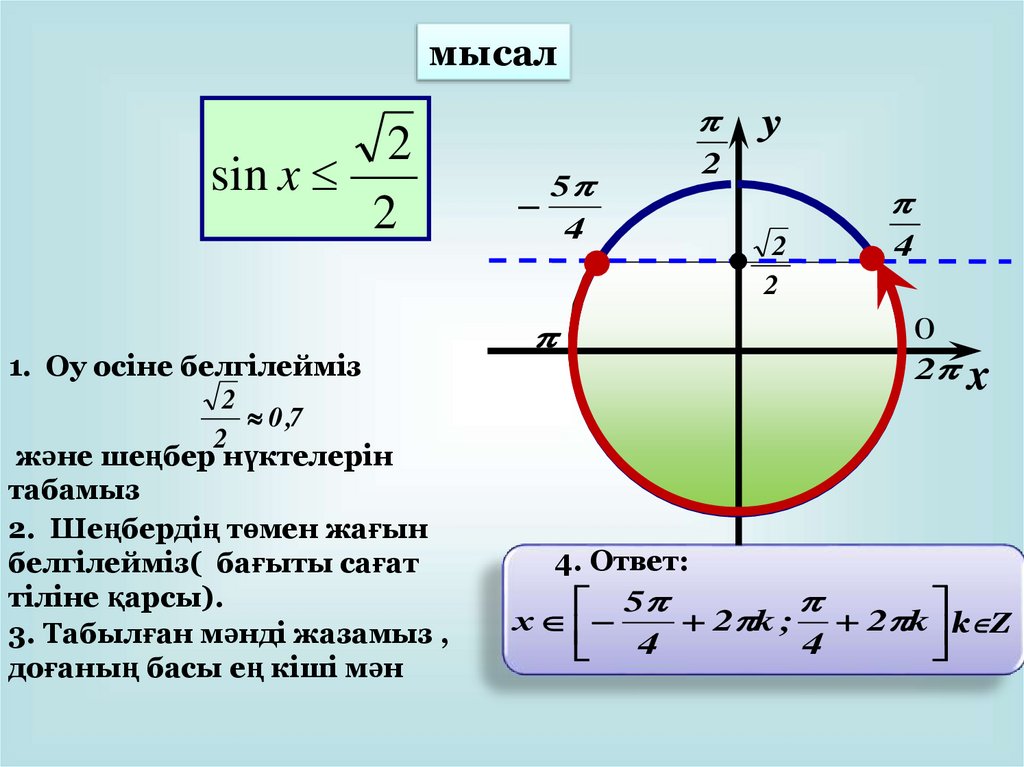
мысал
2
sin x
2
1. Оу осіне белгілейміз
2
0 ,7
2
және шеңбер нүктелерін
табамыз
2. Шеңбердің төмен жағын
белгілейміз( бағыты сағат
тіліне қарсы).
3. Табылған мәнді жазамыз ,
доғаның басы ең кіші мән
5
4
y
2
2
2
4
0
2 x
4. Ответ:
5
х
2 k ; 2 k k Z
4
4

7.

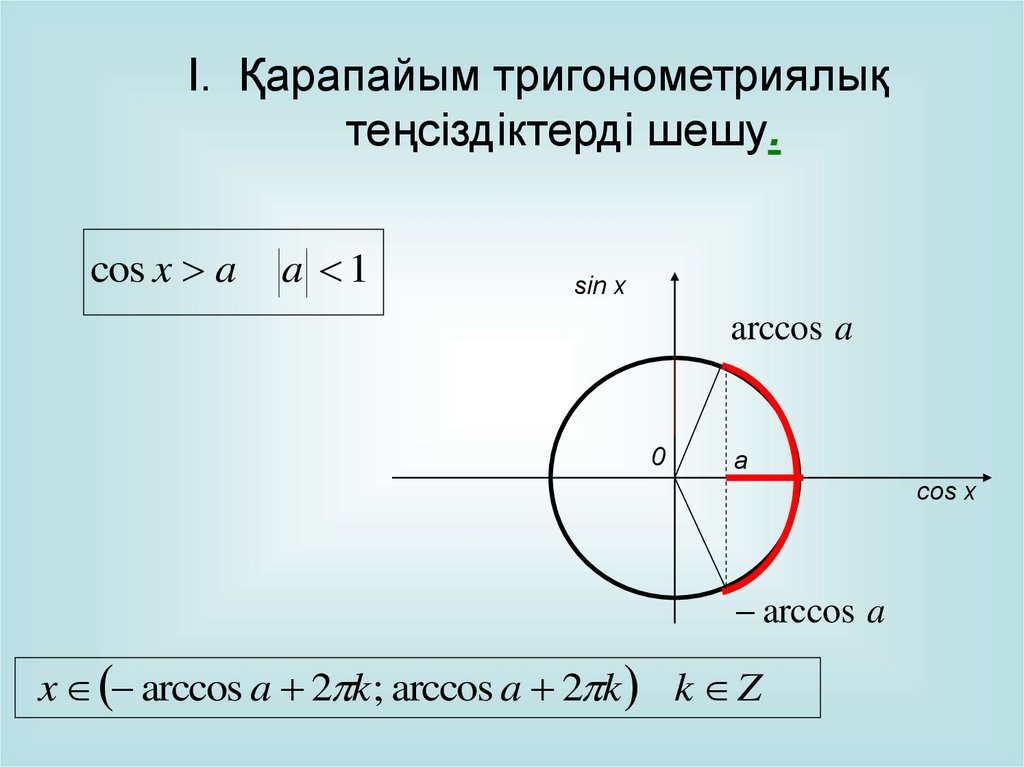
I. Қарапайым тригонометриялық
теңсіздіктерді шешу.
cos x a
a 1
sin x
arccos a
0
a
cos x
arccos a
x arccos a 2 k; arccos a 2 k k Z

8.

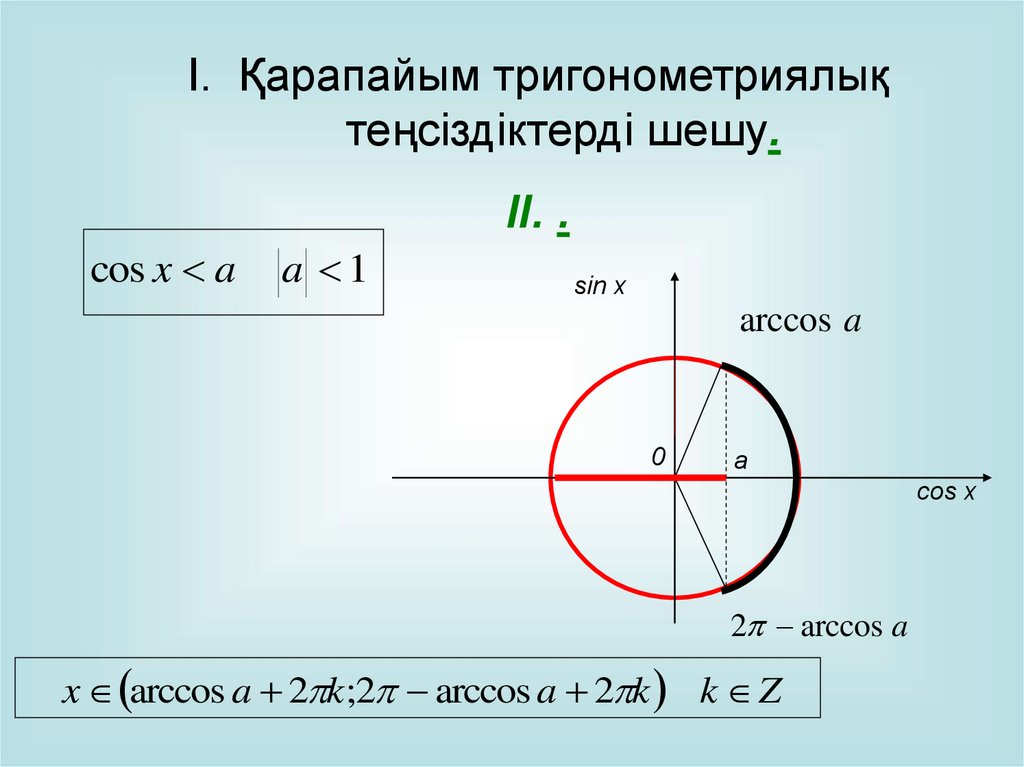
I. Қарапайым тригонометриялық
теңсіздіктерді шешу.
II. .
cos x a
a 1
sin x
arccos a
0
a
cos x
2 arccos a
x arccos a 2 k;2 arccos a 2 k k Z

9.

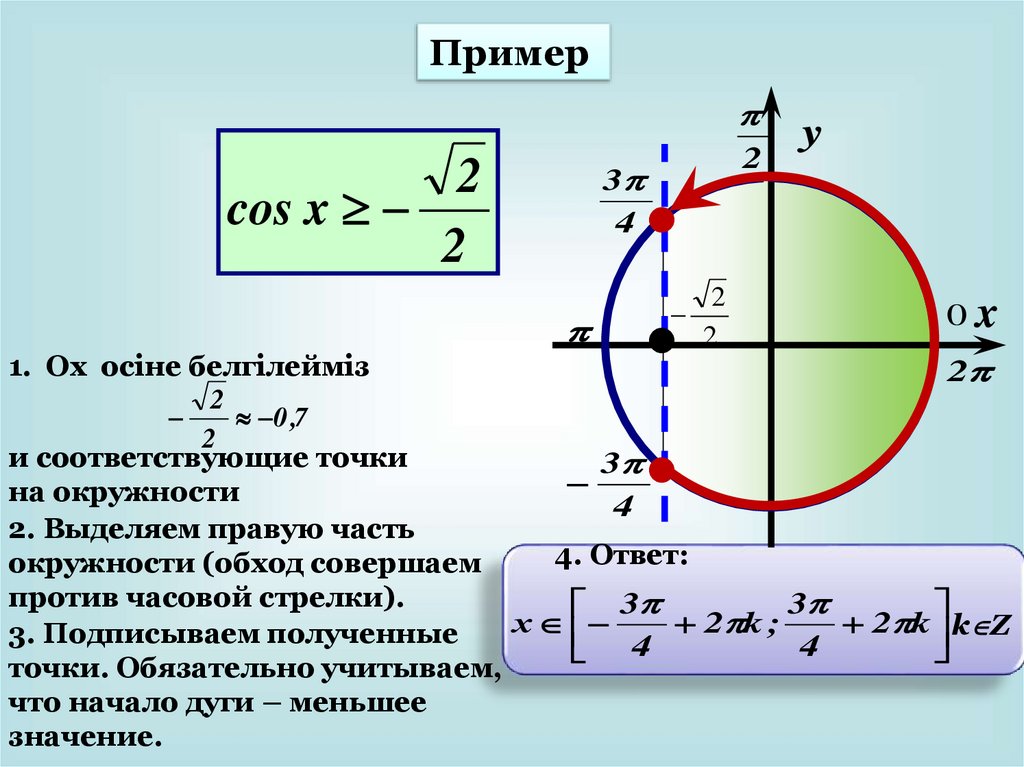
Пример
2
3
4
2
cos x
2
2
2
y
0x
1. Ох осіне белгілейміз
2
2
0 ,7
2
и соответствующие точки
3
на окружности
4
2. Выделяем правую часть
4. Ответ:
окружности (обход совершаем
против часовой стрелки).
3
3
х
2
k
;
2
k
k Z
3. Подписываем полученные
4
4
точки. Обязательно учитываем,
что начало дуги – меньшее
значение.

10.

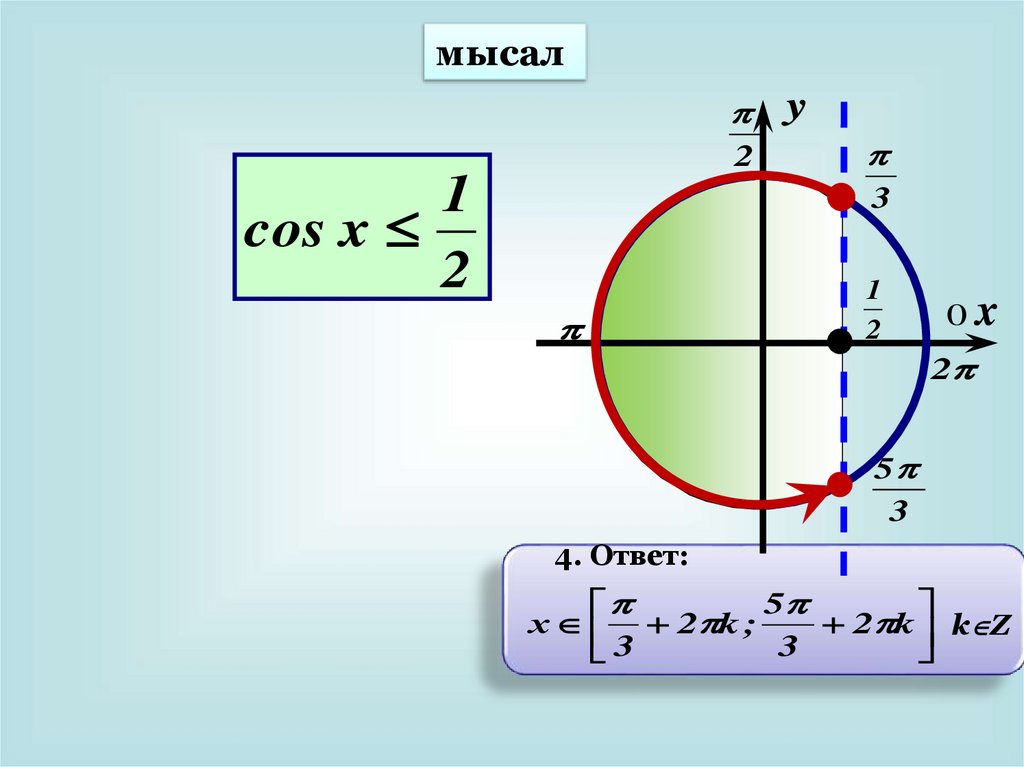
мысал
2
1
cos x
2
y
3
1
2
0x
2
5
3
4. Ответ:
5
х 2 k ;
2 k k Z
3
3

11.

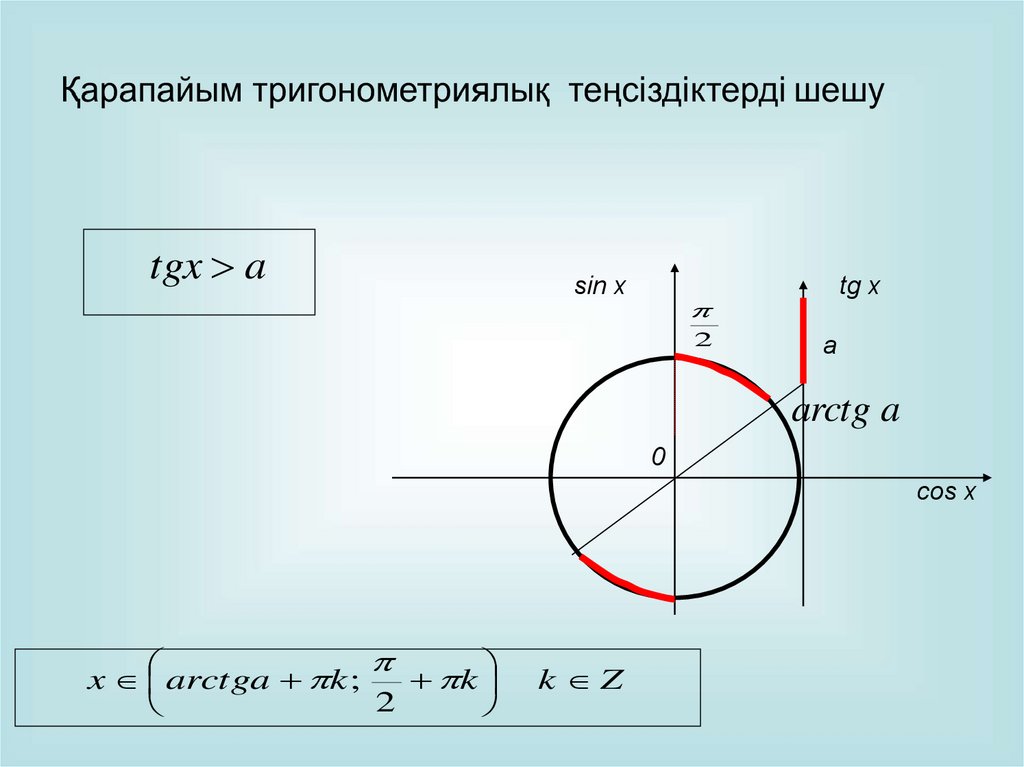
tgx a
sin x
tg x
2
a
arctg a
0
cos x
x arctga k ;
k
2
k Z

12.

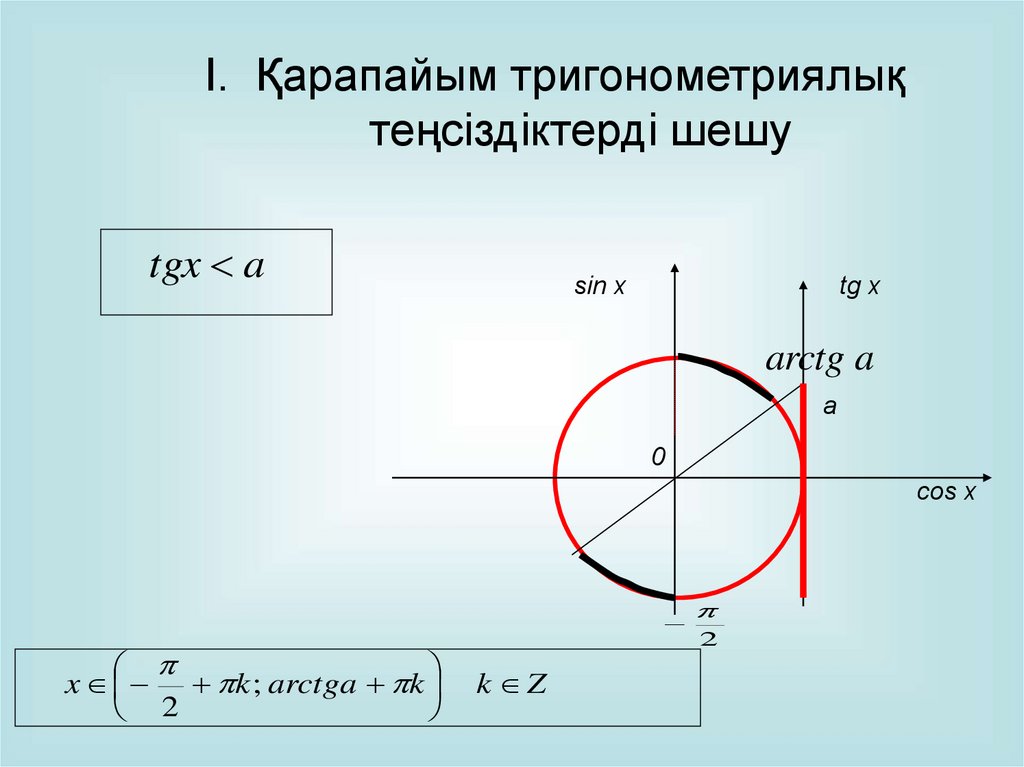
I. Қарапайым тригонометриялық
теңсіздіктерді шешу
tgx a
sin x
tg x
arctg a
a
0
cos x
x k ; arctga k
2
k Z
2

13.

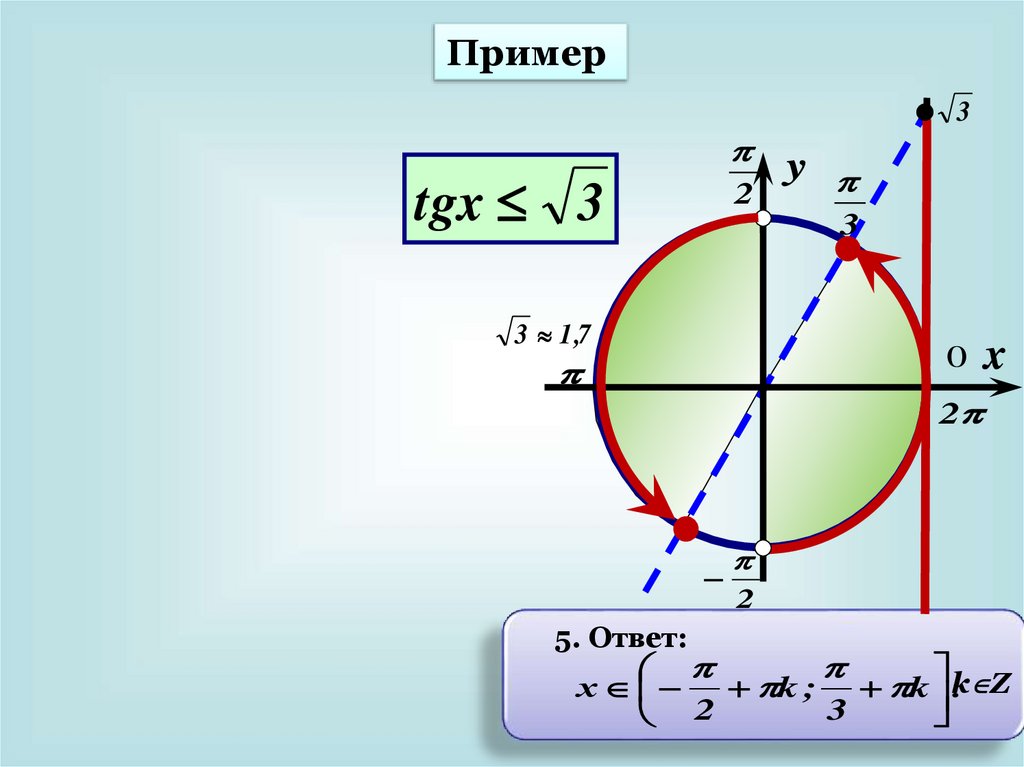
Пример
3
tgx 3
2
3
3 1 ,7
0 x
2
5. Ответ:
y
2
Z
х
k ; k k
.
3
2

14.

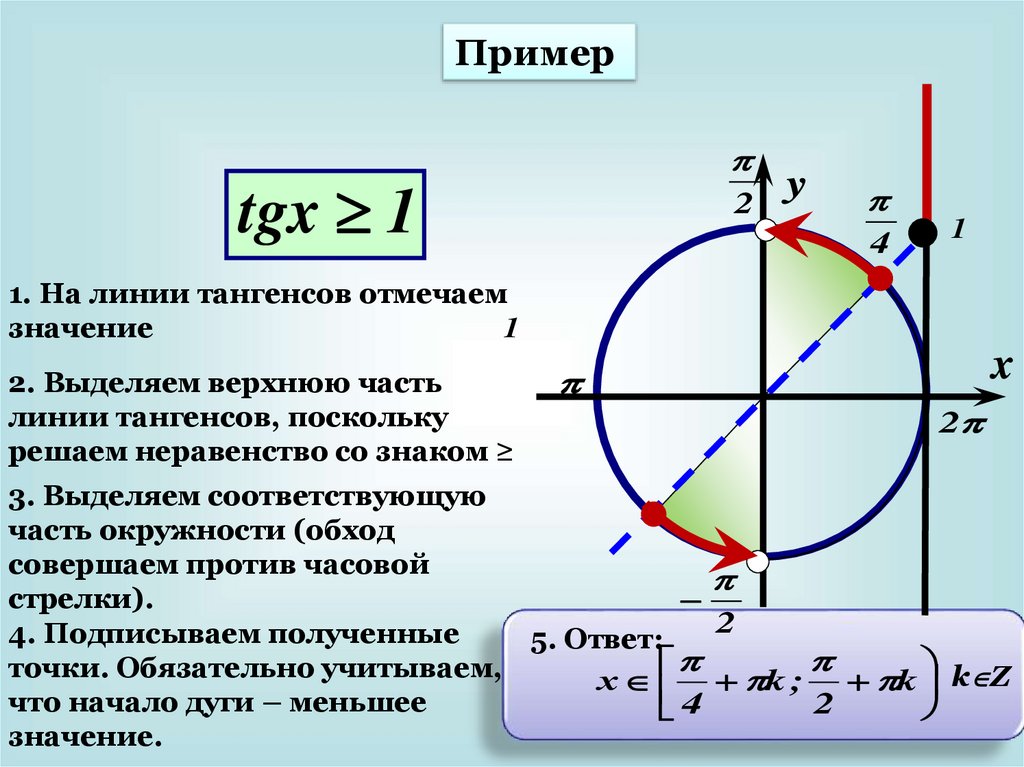
Пример
tgx 1
2
y
4
1
1. На линии тангенсов отмечаем
1
значение
2. Выделяем верхнюю часть
линии тангенсов, поскольку
решаем неравенство со знаком ≥
x
2
3. Выделяем соответствующую
часть окружности (обход
совершаем против часовой
стрелки).
2
4. Подписываем полученные
5. Ответ:
точки. Обязательно учитываем,
х k ; k k Z
что начало дуги – меньшее
2
4
значение.

15.

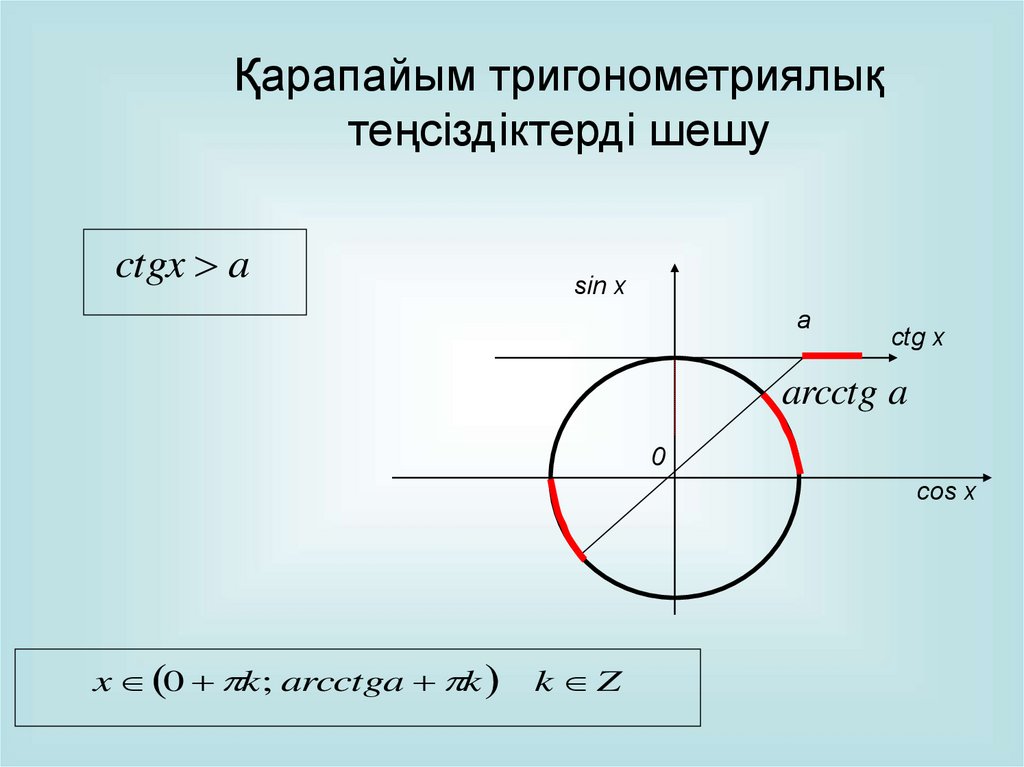
Қарапайым тригонометриялық
теңсіздіктерді шешу
ctgx a
sin x
a
сtg x
arcctg a
0
cos x
x 0 k ; arcctga k
k Z

16.

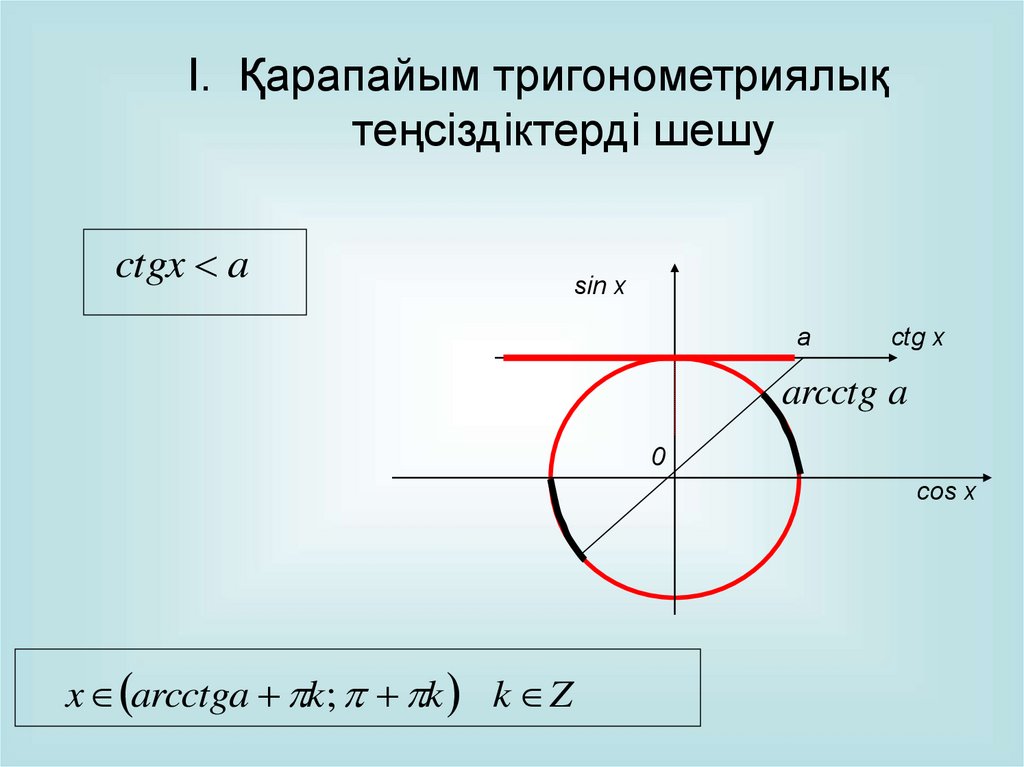
I. Қарапайым тригонометриялық
теңсіздіктерді шешу
ctgx a
sin x
a
сtg x
arcctg a
0
cos x
x arcctga k; k k Z