Similar presentations:
Тригонометриялық теңдеулерді шешудің тәсілдірі
1.
№1 орта мектебіТақырыбы:
Тригонометриялық теңдеулерді
шешудің тәсілдірі
математика пән мұғалімі: Б.А.Кудинова
2.
МақсатыОқушылардың қарапайым тригонометриялық теңдеулердің
түбірлерін анықтау механизмін түсінуін және оны меңгеруін
қалыптастыру арқылы, алған біліктерін тригонометриялық
теңдеулерді шешу барысында қолдана білу бейімділіктерін
қалыптастыру.
Әдісі: Деңгейлеп оқыту технологиясы
Түрі: Біліктілік пен дағдыны игеру және қалыптастыру сабағы
3.
Сабақ құрылымы:І. Оқушылық деңгей;
ІІ. Алгоритімдік деңгей;
ІІІ. Эвристикалық деңгей;
IV. Шығармашылық деңгей.
І. Оқушылық деңгей (Ауызша сұрақ)
1. Тригонометриялық теңдеулерді шешуде не
істейміз?
2. Нені білу керек?
3. Тригонометриялық теңдеулерді шешу үшін қандай
тәсілдерді қолданамыз?
4.
Тақтада берілген теңдеулердің ішінентәсілдермен шығарылатынын көрсетіңдер:
қайсысы
а) Квадрат теңдеуге келтіріп шығаратын теңдеу
мына
(4,10,8)
ә) Біртекті теңдеулерге келтіріп шешу
(1,5,9)
б) Дәрежені төмендету арқылы шығаратын теңдеу
(2)
в)Тригонометриялық функциялардың көбейтіндісін қосындыға (айырмаға)
келтіру арқылы шығарылатын есептер
(6,7)
г) Универсал (әртүрлі) тригонометриялық алмастыру арқылы шығару (11)
1) 2 sin x cos x 5 sin x cos x
2
2
3
2
2)
sin 2 x cos 2 2 x sin 2 3x
3)
cos x sin 7 x cos 3x sin 5x
7)
sin x sin 2 x sin 3x sin 4 x 0
8)
2 cos 2 x 3 sin 2 x 2 sin x 0
9)
cos 2 x 3 sin 2 x 2 3 sin x cos x 3
3
sin 2 x cos 2 x
3
4)
sin 2 x 2 sin x 3 0
10)
sin 2 x
5)
2 cos x sin x 0
11)
sin x cos x 1
6)
sin x sin 3x sin 5x sin x
5.
ІІ. Алгоритмдік деңгей. Тест (Деңгейлік тапсырма)Тапсырма
І нұсқа
sin x
sin 2 x
ІІ нұсқа
1
2
sin x
2
2
sin 2 x
sin x 1
3
Жауаптары
1
2
2
2
sin x 1
3
1
2
1 k k
1 k
1 k
1 k 1
6
8
2
5
2 k
6
k
6
6
8
3
2 k
2
2 k
k
4
1 k 1
k
6
8
6
2
6
k
k
2 k
8
2
k
5
2 k
6
6.
ІІІ. Эвристикалық деңгей (Математикалық диктант)І нұсқа
ІІ нұсқа
1. Анықтамасын тұжырымдаңдар
а) санның арксинусы
ә) санның арккатангисі
а) санның арккосинусы
ә) санның арктангесі
2. Теңдеулердің шешімдерінің жалпы түрінің формулаларын
жазыңдар
sin x a
cos x a
3. Теңдеулердің шешімдерінің дербес түрлерінің формуласын
жазыңдар
cox a
sin x a
7.
IV. Шығармашылық деңгей (Ойлан тап!)Қарапайым тригонометриялық теңдеуді
шешу:
1
cos 3 x
4 2
Өте қолайлы шығару тәсілдері:
sin 3x sin x
Кводрат теңдеуге келтіріп шығаратын
теңдеу:
2 cos 2 x 5 cos x 2 0
Біртекті тригонометриялық теңдеу:
7 sin 2 x 8 sin x cos x 15 cos 2 x 0
1
sin 2 2 x
2
Дәрежені төмендету арқылы
шығарылатын теңдеу:
Тригонометриялық функцияның
көбейтіндісін қосынды арқылы
шығару:
sin 3x cos x sin 5x cos 3x
Тригонометриялық функцияның
қосындыны көбейтіндіге келтіріп
шығару:
cos x cos 5x cos 3x cos 7 x
Қосымша бұрыш енгізу тәсілі:
sin x 3 cos x 1
Универсал тригонометрияның
алмастыру әді:
sin 2 x tgx 2
8.
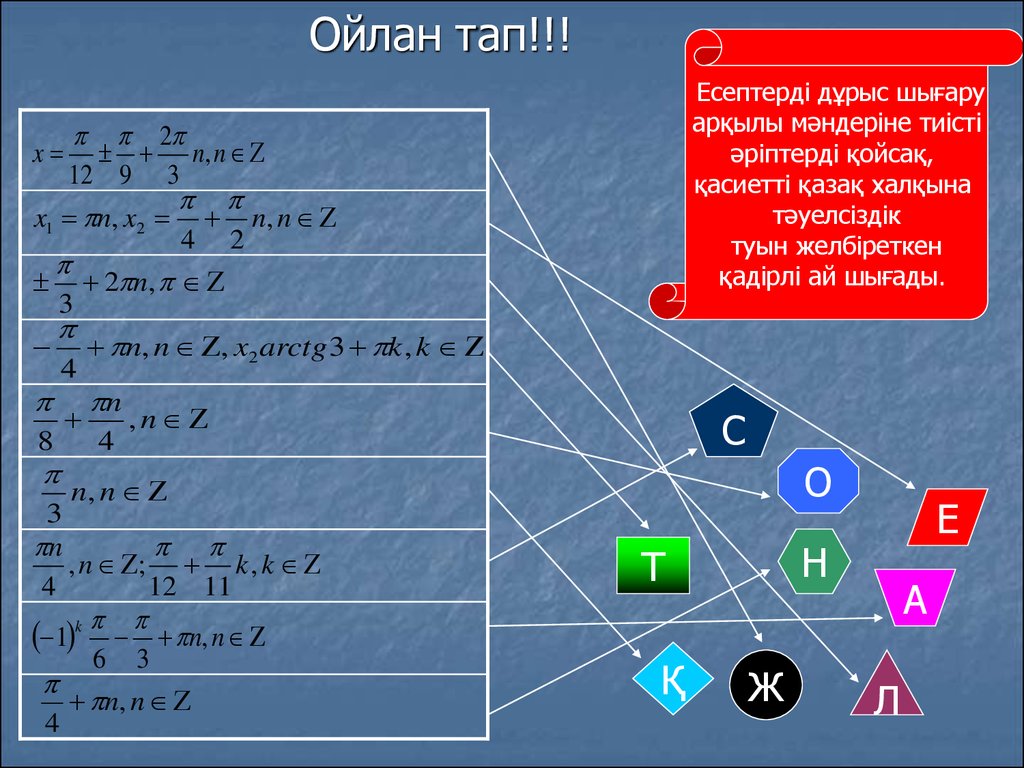
Ойлан тап!!!2
n, n
12 9 3
x1 n, x2 n, n
4 2
2 n,
3
n, n , x2 arctg 3 k , k
4
n
,n
8
4
n, n
3
n
, n ; k , k
4
12 11
1 k n, n
6 3
n, n
4
Есептерді дұрыс шығару
арқылы мәндеріне тиісті
әріптерді қойсақ,
қасиетті қазақ халқына
тәуелсіздік
туын желбіреткен
қадірлі ай шығады.
x
С
О
Н
Т
Қ
Е
Ж
А
Л
9.
Қарапайым тригонометриялық теңдеулершешімдерінің жалпы түрі
sin x a, x 1 arcsin a n, n
n
cos x a, x arccos a 2 n, n
tgx a, x arctga 2 n, n
ctgx a, x arcctga 2 n, n
sin x 1
Шешімдердің дербес түрлері
sin x 1
sin x 0
x 2 n, n
2
x
cos x 1
cos x 1
2
2 n, n
x n, n
cos x 0
x 2 n, n x 2 n, n x
tgx 1
x
4
tgx 1
n, n x
4
2
tgx 0
n, n
n, n x n, n
10.
ҚорытындыБүгінгі сабақта біз тригонометриялық теңдеулерді
шешудің әртүрлі тәсілдерін қолдану арқылы көптеген
есептерді шығарып дағдылану нәтижесінде, тәжірибемен
ғана келетінін көрдік.
11.
Назар қойыптыңдағандарыңызға рахмет!!!










 mathematics
mathematics








