Similar presentations:
Тригонометриялық теңсіздіктерді шешу
1. Тригонометриялық теңсіздіктерді шешу
2.
3. Қарапайым тригонометриялық теңсіздіктер
sinх>asinх<a
sinх≥a
sinх≤a
cosх>a
cosх<a
cosх≥a
cosх≤a
tgх>a
tgх<a
tgх≥a
tgх≤a
ctgх>a
ctgх<a
ctgх≥a
ctgх≤a
4. Теңсіздіктерді шешу алгоритмі
1. Бірлік шеңбер сызамыз.2. Оның бойынан синусы (косинусы, тангенсі) аға тең болатын нүктені табамыз.
3. Сол нүкте арқылы перпендикуляр түзу
жүргіземіз. Шеңбермен қиылысу нүктелерін
белгілейміз.
4. Есептің берілгеніндегі теңсіздік таңбасына
сәйкес, барлық нүктелердің жиыны болатын
доғаны жуан қара сызықпен бояймыз.
5. Шешімін бастапқы нүктеден соңғы нүктесіне
қарай сағат тілінің қозғалысына қарсы бағытта
жүре отырып аламыз.
6. Функцияның периодтылығын ескереміз.
7. Жауабын жазамыз.
5.
yx
7
6
1
2
6
№1
1
sin х
2
7
х [ 2 n;
2 n], n Z .
6
6
6.
y5
4
2
2
4
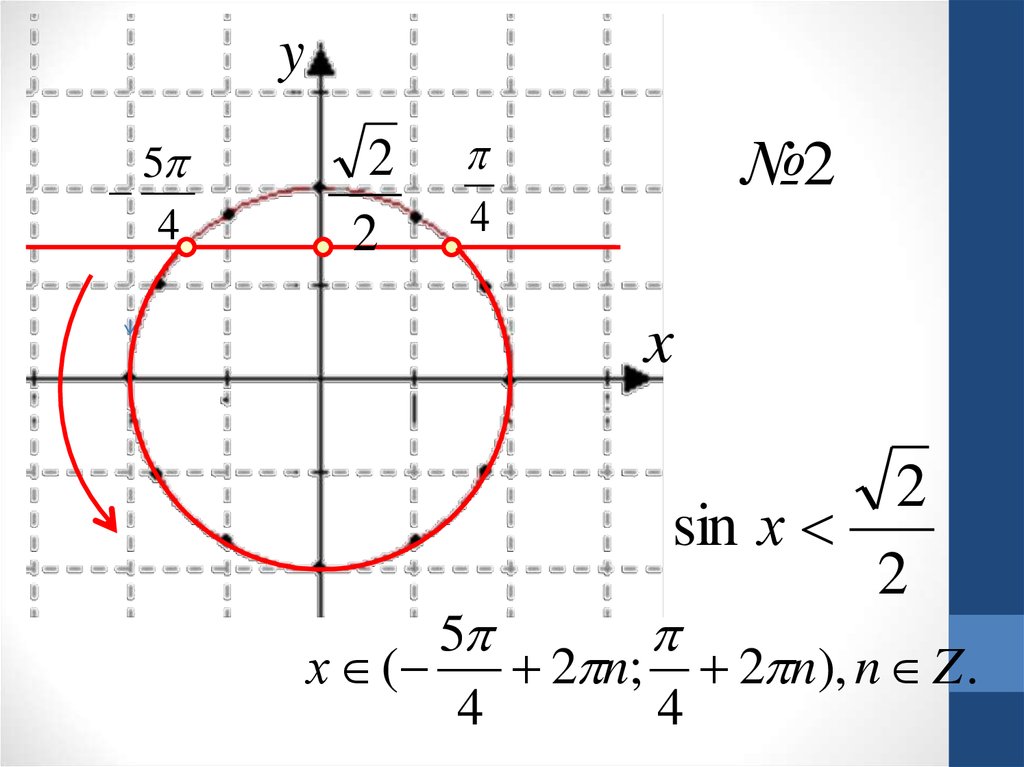
№2
x
2
sin х
2
5
х (
2 n; 2 n), n Z .
4
4
7.
y3
1
2
x
5
3
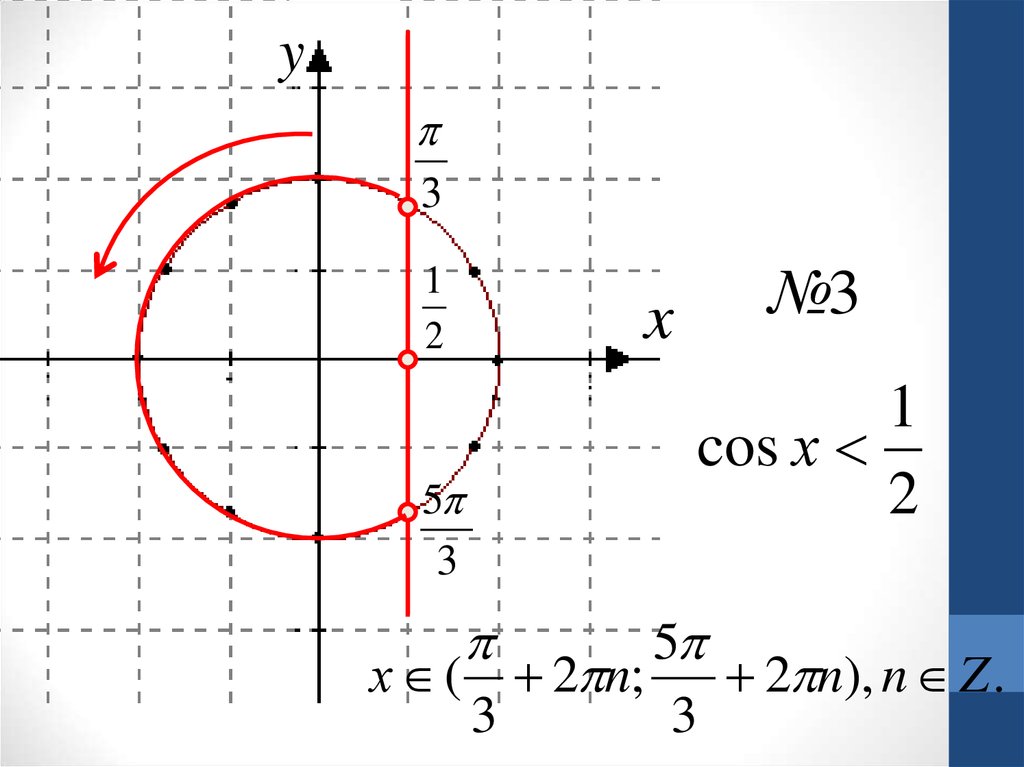
№3
1
cos х
2
5
х ( 2 n;
2 n), n Z .
3
3
8.
y5
6
5
6
3
2
x
№4
3
cos х
2
5
5
х [
2 n;
2 n], n Z .
6
6
9.
№53
2
3
2
tgх 3
х ( n; n), n Z .
2
3
10.
№63
2
tgх 3
3
2
х [ n; n), n Z .
3
2
11.
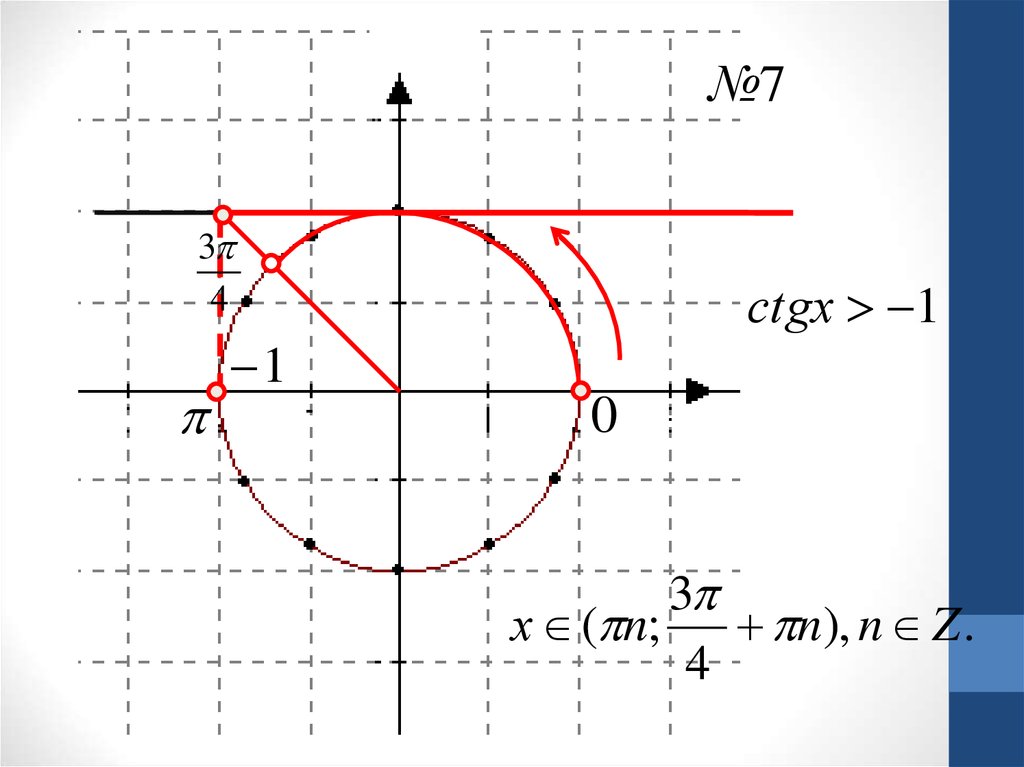
№73
4
сtgх 1
1
0
3
х ( n;
n), n Z .
4
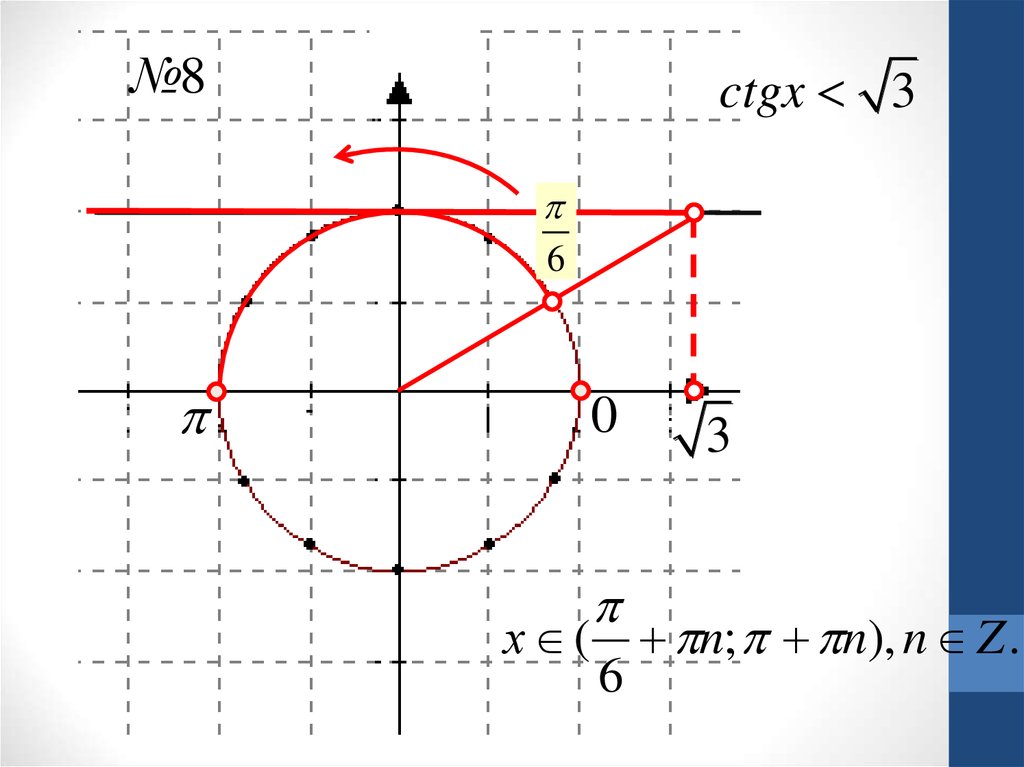
12.
№8ctgx 3
6
0
3
х ( n; n), n Z .
6
13. Өздік жұмыс 1-нұсқа 2-нұсқа 1)sin x<- 1)sin x < 1/2 2)cos x< -1/2 2)cos x≥ /2 3)tg2x -1 3)tg 3x ≤ 1 4)sin(2x–π/6)- /2
Өздік жұмыс1-нұсқа
2-нұсқа
1)sin x<- 2 / 2
1)sin x < 1/2
2)cos x< -1/2
2)cos x≥ 3/2
3)tg2x -1
3)tg 3x ≤ 1
4)sin(2x–π/6) - 3/2 4)cos(3x–π/4)≤- 2/2
5) 2cos(4x–π/6)>1 5)2sin(x/2+π/4) ≥ -1










 mathematics
mathematics








