Similar presentations:
Көрсеткіштік функция. Көрсеткіштік теңдеулер мен теңсіздіктер
1. Көрсеткіштік функция. Көрсеткіштік теңдеулер мен теңсіздіктер.
2. Дәреже
Дәреже қасиеттеріФункция
1. Анықтамасы
2. Қасиеттері
3. График
Теңдеулер
1. Анықтамасы
2. Кейбір көрсеткіштік теңдеулерді шешу жолдары
Теңсіздіктер
1. Көрсеткіштік теңсіздіктерді шешу жолдары
3. Көрсеткіштік функция
f x axтүрінде берілген функция көрсеткіштік деп
аталады, мұндағы a- дәреженің негізі деп аталады және ол
нақты оң сан, a≠0.
4.
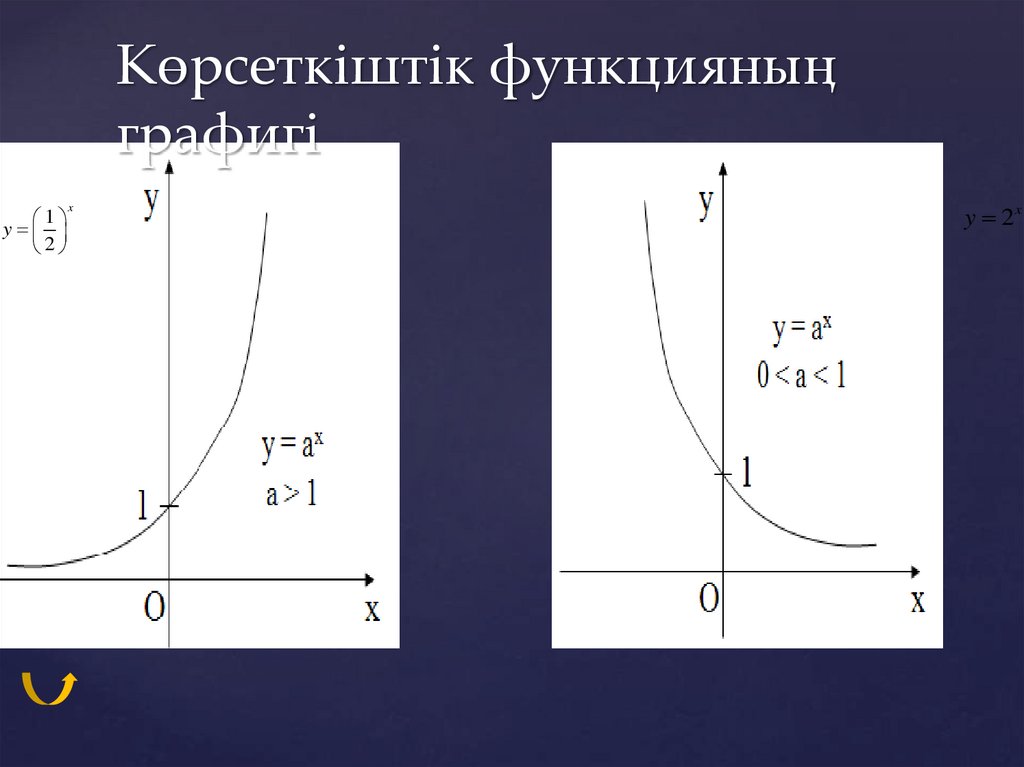
Көрсеткіштік функцияның қасиеттеріa>1
0<a<1
Анықталу облысы
D(y)=R
D(y)=R
Мәндерінің жиыны
Е(y)=(0;+∞)
Е(y)=(0;+∞)
Жұп, тақтығы
Жұп та, тақ та емес
Жұп та, тақ та емес
Функция нольдері
(0;1) OY
OX өсімен қиылысу
нүктесі жоқ
(0;1) OY
OX өсімен қиылысу нүктесі
жоқ
Таңба тұрақты
аралықтары
Бүкіл сан өсінде оң
мәндер қабылдайды
Бүкіл сан өсінде оң мәндер
қабылдайды
Өсу, кему
аралықтары
(-∞;+∞) өседі
(-∞;+∞) кемиді
Экстремум
нүктелері
жоқ
жоқ
асимптотасы
У=0 горизонталь
У=0 горизонталь
E ( y)
5. Көрсеткіштік функцияның графигі
1y
2
x
y 2x
6. Көрсеткіштік теңдеулер
Негізі тұрақты ,ал дәреженің көрсеткішінде айнымалы болса ондайтеңдеулерді көрсеткіштік теңдеу деп атайды.
Қарапайым көрсеткіштік теңдеуге келесі түрдегі теңдеу жатады:
а b
х
мұнда a және b – кез келген оң сан, (а 1), ал х – кезкелген алгебралық
өрнек.
7. Кейбір қарапайым көрсеткіштік теңдеулерді шешу жолдары
f ( x)a
1 , мұнда a 0 , a 1
1.
1 a0
f ( x) 0
a f ( x) a
2.
f ( x)
a f ( x) b
3.
Бұл теңдеуді шешу үшін оның оң және сол жағын бірдей негізге
келтіру керек. Әрі қарай жоғарыдағы 2-түрдегі теңдеу секілді
8.
A0 x kx m0 A1 x kx m1 ... An x kx n B2x
x
A
a
A
a
A2 0
4. 0
1
x b
ax b
x c
Ba
C
5.Aa
жаңа айнымалы енгіземіз:
x
2
x
2
6.A0 a A1a b A2b 0
квадрат теңдеуге келтіреміз:
x
b 0
x
7.
екінші дәрежелі біртекті теңдеу:
,
9. Мысалдар:
2cos 2 x 13
1
x1. R
,
2cos 2 x 1
3
3
0
2cos2 x 1 0
2cos 2 x 1
1
cos 2 x
2
1
2 x arccos( ) 2 n, n Z
2
x n
, n Z
3
жауабы:
x
3
n, n Z
10. Мысалдар:
2.14
27
3
3
9
3
3
3
3
3 x 1
27
1
(3 x 1)
2
1
(3 x 1)
2
2
3
3 2
3 2
1
(3x 1) 2
2
3
3
1
x 2 0
2
2
3
1
x 1
0
2
2
3
3
x
2
2
x 1
жауабы: x=1
11. Тапсырма
2а)3 x 3 23 x 1 2023 x 1 (2 3) 20
2
3 x 1
б)
2
3 x 1
4
2 x
1
2
22
2 x
1
2
42 x 3
24 x 3
3 x 1 2
2 x
1
2
2 x
1
2
3
3
2 x
24 x 2 4 x 1 3
3 x 3
1
2
2 x
4 x 1
1
2
2 4 x 1
2 4 x 1
2 x
3
1
2
x 1 2 (2 1) 3 (1 3)
1
2 x
4 x 1
x 1 3 2 4 3 2
2
2
4 x 3
2 x
3
3
2(2 x )
2
3
2
2 x
3
3
3
2
12. Көрсеткіштік теңсіздіктерді шешу жолдары:
1. а)б)
ax b
ax b
2.
a x m a x n a x b
3.
ax ax b 0
,a 0
,a 0
13. Мысалдар:
1. а)3 81
x
3 3
x
4
y 3t
монотонно өседі (3>1), сондықтан да соңғы теңсіздік келесі
теңсіздікпен бірмәндес:то последнее неравенство равносильно:
X>4
x 4;
жауабы:
x 4;
14.
x1
1
3 81
x
4
1 1
1. б)
3 3
x 4
функция монотонно кемиді , сондықтан теңсіздік келесі теңсіздікпен
бірмәндес:
x ( ;4)
Ответ : x ( ;4)
Жауабы:
15. Дереженің қасиеттері:
а n a a a ... a6)(a ) a
m n
1)a 1
0
2)a
n
4)a a a
n n
n
8)(a / b) a / b
n
n
3)a n a m
n
mn
7)(ab) a b
1
n
a
m
n
m
n N
9) ab a b
n
n
m n
5)a m a n a m n
n
n
10) a n a
n
m
m






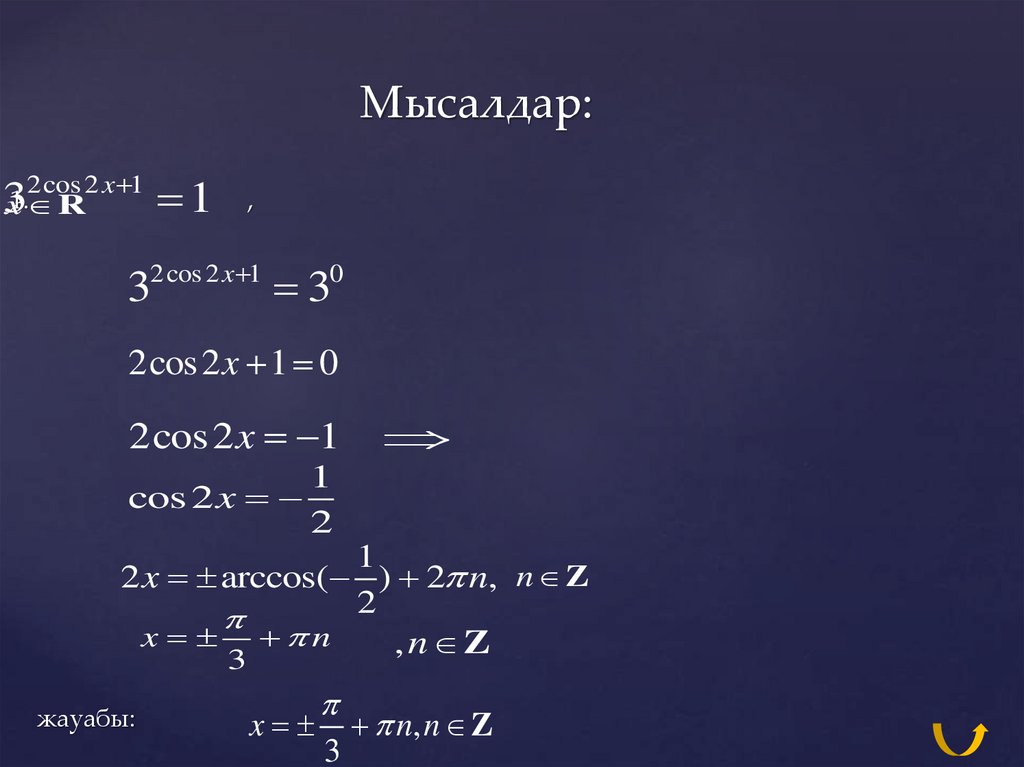






 mathematics
mathematics








