Несобственные интегралы

1.

Несобственные
интегралы
ПОДГОТОВИЛИ СТУДЕНТЫ 2-ТИД-7
ВГ
Романенко П.
Фоменко В.
Гаевский В.
Абаджонов Ф.

2.

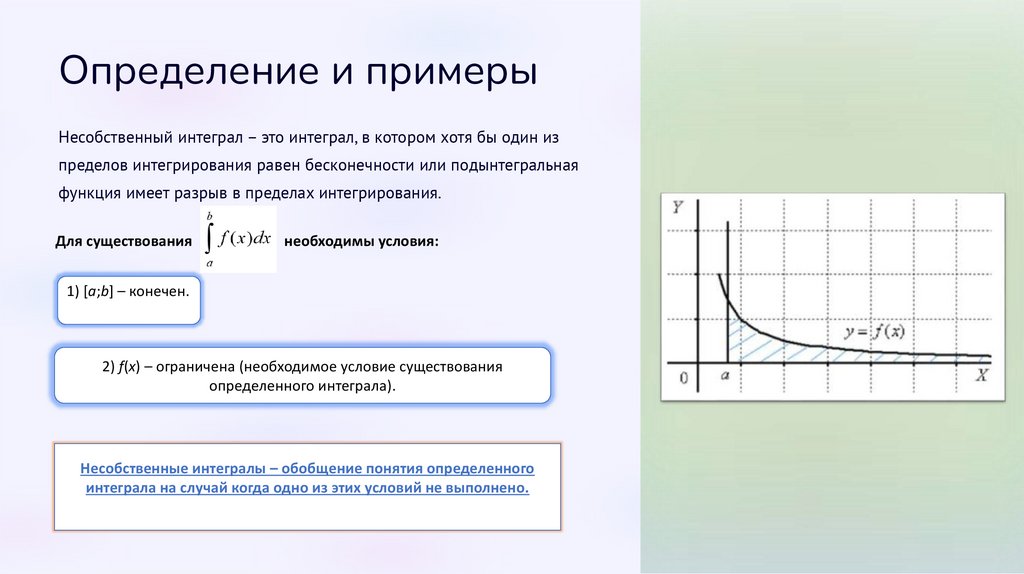
Определение и примеры
Несобственный интеграл – это интеграл, в котором хотя бы один из
пределов интегрирования равен бесконечности или подынтегральная
функция имеет разрыв в пределах интегрирования.
Для существования
необходимы условия:
1) [a;b] – конечен.
2) f(x) – ограничена (необходимое условие существования
определенного интеграла).
Несобственные интегралы – обобщение понятия определенного
интеграла на случай когда одно из этих условий не выполнено.

3.

Типы несобственных интегралов
Несобственные интегралы бывают двух типов:
Интегралы с бесконечными пределами
Интегралы с разрывной функцией
Интеграл, в котором один из пределов интегрирования
Интеграл, в котором подынтегральная функция имеет
равен бесконечности.
разрыв в пределах интегрирования.

4.

Конвергенция и
дивергенция
1
Конвергенция (сходимость)
__
Интеграл имеет конечное значение.
2
Дивергенция (расходимость)
Интеграл имеет бесконечное значение.
__

5.

Методы вычисления
Существуют различные методы вычисления несобственных интегралов:
МЕТОД ПОСТАНОВКИ
ПРИМЕР:

6.

Методы вычисления
Существуют различные методы вычисления несобственных интегралов:
МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
ПРИМЕР:

7.

Свойства неопределённого
интеграла

8.

Применения несобственных
интегралов
Несобственные интегралы имеют широкое применение в различных
областях, включая физику, статистику и вероятность.
Физические задачи
Решение задач, связанных с силами, работой и энергией.
Статистика и вероятность
Вычисление вероятностей и ожидаемых значений.

9.

Практические примеры
Задача 1
1
Решить неопределённый интеграл методом замены переменной
Задача 2
2
Решить неопределённый интеграл методом интегрирования по частям

10.

Практические примеры
ОТВЕТЫ:
Задача 1
1
Решить неопределённый интеграл методом замены переменной
Задача 2
2
Решить неопределённый интеграл методом интегрирования по частям

11.

СПАСИБО ЗА ВНИМАНИЕ