Несобственные интегралы

1. 7. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

b
f ( i ) xi
n
Определенный интеграл f ( x)dx lim
a
1) для непрерывных функций,
2) на конечном промежутке.
n
i 1
существует:

2. 7.1. Несобственные интегралы I-го рода

Определение
. Это интегралы от непрерывных функций в бесконечном промежутке.
Пусть f (x) определена и непрерывна при всех значениях x таких,
что a x . Рассмотрим
b
J (b) f ( x)dx .
a
(7.1.1)
Этот интеграл имеет смысл при любом b a . При изменении b интеграл
меняется, он является непрерывной функцией b . Рассмотрим вопрос о
поведении этого интеграла при b .

3. О п р е д е л е н и е

Определение
Если существует конечный предел
b
lim f ( x)dx ,
b
a
то этот предел называется несобственным интегралом от функции f (x) на
интеграле [a, [ и обозначается
f ( x)dx .
a
Итак:
b
(7.1.2)
f ( x)dx lim f ( x)dx .
a
b
a
Говорят, что в этом случае несобственный интеграл
f ( x)dx
существует
a
b
или сходится. Если
f ( x)dx
при b не имеет конечного предела, то
a
говорят, что
f ( x)dx не существует или расходится.
a

4. ПРИМЕРЫ

П р и м е р 1.
1
b
b
1
1
lim
lim
lim
1 1. Сходится.
2
2
b x
b x 1
b b
x
1
dx
dx
b
dx
dx
lim lim ln x 1b lim ln b ln 1 . Расходится.
П р и м е р 2.
b x
b
b
1 x
1
Аналогично определяются несобственные интегралы и для других
бесконечных интервалов:
b
1)
2)
b
f ( x)dx ,
a
f ( x)dx lim
f (x) непрерывна в ] , b] .
a
f ( x)dx
c
f ( x)dx f ( x)dx , f (x) непрерывна на всей числовой оси.
c

5. 7.2. Несобственные интегралы II-го рода

Это интегралы в конечном промежутке от разрывных функций, а именно
уходящих в .
1) Пусть f (x) определена и непрерывна при a x b , при x b функция
либо не определена, либо терпит разрыв. В этом случае нельзя говорить об
b
интеграле
f ( x)dx
как о переделе интегральных сумм, так как f (x) не
a
непрерывна на [a, b] и поэтому этот предел может и не существовать.
b
Интеграл
f ( x)dx
от функции
f (x) , разрывной в точке
x b
a
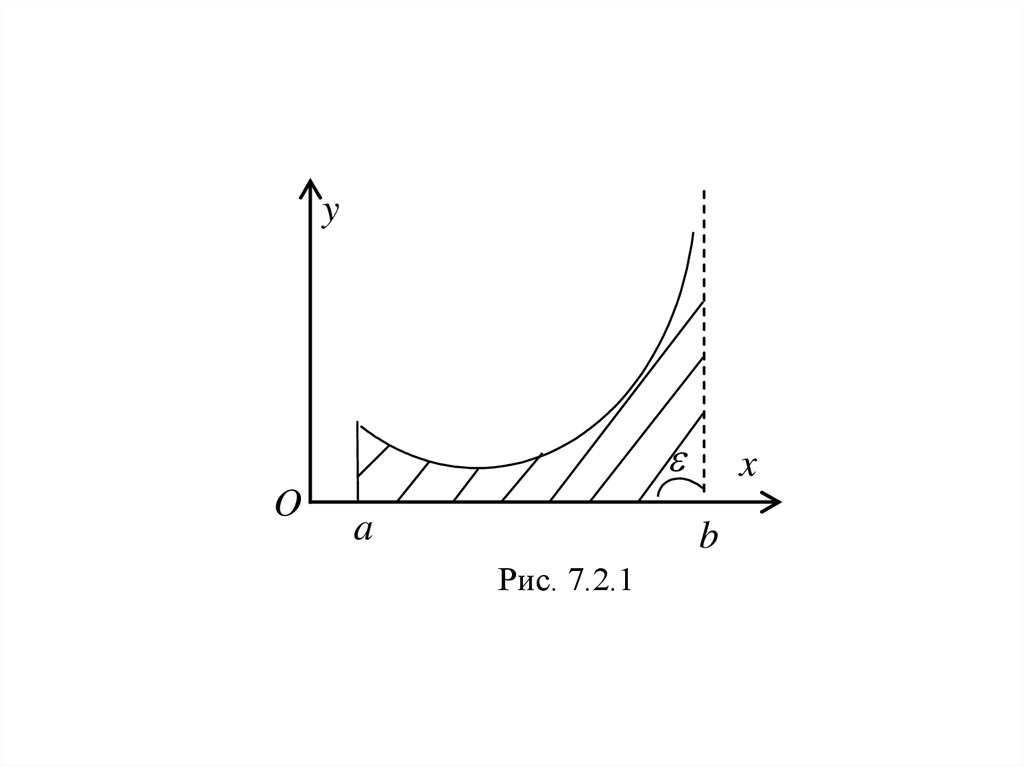
определяется следующим образом (рис. 7.2.1):
b
b
f ( x)dx lim
0
a
f ( x)dx .
(7.2.1)
a
Если предел, стоящий справа существует, то интеграл называется
несобственным интегралом II-го рода. В противном случае говорят, что
несобственный интеграл не существует или расходится.

6.

y
O
a
x
b
Рис. 7.2.1

7.

2) Если f (x) терпит разрыв на левом конце отрезка [a, b] , т.е. при x a , то
по определению (рис. 7.2.2)
b
b
f ( x)dx lim
0
a
f ( x)dx .
(7.2.2)
a
y
x
a
b
Рис. 7.2.2

8.

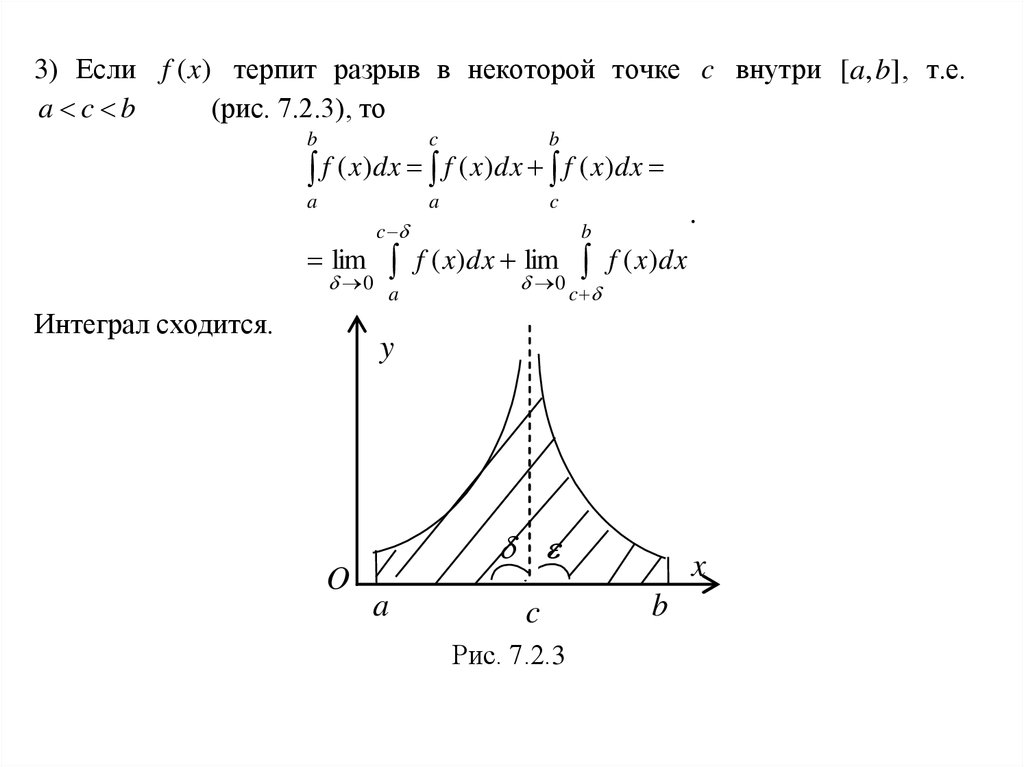
3) Если f (x) терпит разрыв в некоторой точке c внутри [a, b] , т.е.
(рис. 7.2.3), то
a c b
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
lim
c
0
Интеграл сходится.
a
f ( x)dx lim
0
.
b
f ( x) dx
c
y
O
a
c
Рис. 7.2.3
x
b

9. Примеры

1
П р и м е р 1.
0
1
1
dx
dx
lim
lim 2 1 x 0
0
0
1 x
0 1 x
lim 2 1 1 1 2.
0
П р и м е р 2.
1
1
dx 0 dx 1 dx
dx
dx
lim
lim
x 2 x 2 x 2 0 x 2 0 x 2
1
1
0
1
1
1
1
1
1
lim lim lim 1 lim 1 .
0 x 1 0 x 0
0
Интеграл расходится.

10. З а м е ч а н и е

Замечание
Во многих случаях бывает достаточно установить, сходится данный
интеграл или расходится, и оценить его значение. Для этого могут быть
полезными следующие теоремы, которые примем без доказательства.

11. Т е о р е м а 1

Теорема1
Если для всех x ( x a) выполняется неравенство 0 f ( x) ( x) и если
a
a
( x)dx сходится, то f ( x)dx также сходится, при этом
f ( x)dx ( x)dx .
a
a
(7.2.4)

12. Т е о р е м а 2

Теорема2
Если для всех x ( x a) выполняется неравенство 0 ( x) f ( x) , причем
a
a
( x)dx расходится, то f ( x)dx также расходится, при этом
f ( x)dx ( x)dx .
a
a
(7.2.5)

13. З а м е ч а н и е

Замечание
В теоремах 1 и 2 рассматривались несобственные интегралы от
неотрицательных функций. Для случая f (x) , меняющей знак в
бесконечном интервале, имеет место следующая теорема.
Т е о р е м а 3. Если интеграл
f ( x) dx сходится, то сходится и интеграл
a
f ( x)dx .
(7.2.6)
a
В этом случае последний интеграл называется абсолютно сходящимся.
З а м е ч а н и е. Аналогичные теоремы имеются и для интегралов II-го
рода.