Лекция 3(ВМ) (студентам)

1.

ТЕОРИЯ МЕТОДА СЕТОК
ДУЧП - уравнение, в которое входит неизвестная функция нескольких
переменных y(x) и ее частные производные.
Пример.
2u
2u
2
3
t
x
0,5
2
2
t
x
u ' 'tt 3u ' 'xx t x 2 0,5
Также задаются:
• область изменения аргументов;
• начальные условия;
• граничные условия.
Вместо аналитического решения ДУЧП ищется численное решение – значения
функции y(x) в некоторых точках области изменения переменных.

2.

Универсальный метод численного решения ДУЧП - метод конечных разностей.
Процедура преобразования исходной задачи:
Область непрерывного изменения аргумента -> область дискретного изменения.
Дифференциальный оператор -> разностный оператор (уравнение).
Краевые и граничные условия -> разностный аналог.
Задача решения ДУЧП -> задача решения системы алгебраических уравнений.
Совокупность разностных уравнений, аппроксимирующих исходное ДУЧП и
дополнительные условия, называется разностной схемой.

3.

Множество точек непрерывной переменной x называется сеткой wh={xi, i=0,1,…,n},
отдельные точки xi – узлами сетки.
Будем рассматривать равномерные сетки.
Функция yh = {yi} = {y(xi)}, определенная в узлах сетки, называется сеточной.
Выбор сетки влияет на свойства разностного решения: близость к точному
решению и т.д. Метод сеток - замена непрерывных функций на сеточные.
Сеточная функция yh = {yi} = {y(xi)} представляется вектором
Y = (y0, y1, ..., yn-1, yn).
Рассматривается множество сеток {wh}, зависящих от шага h как от параметра. Т.о.,
сеточные функции зависят от параметра h.
Если сетка wh неравномерна, под h следует понимать вектор h = [h1,h2,..,hn].

4.

Функции u(x) непрерывного аргумента
x G
являются элементами некоторого функционального пространства U.
Множество сеточных функций uh(x) образует
конечномерное пространство сеточных функций.
пространство
Uh
Для нормы ||u||U в пространстве U вводится сеточный аналог – норма ||uh||Uh.
Пример.
Пространство непрерывных функций U = C:
u U max y ( x)
x G
____________________
Пространство функций, квадраты которых интегрируемы U=L2: .
uU
u ( x)dx
2
x G
_______________________
-

5.

Пусть u(x) – решение исходной непрерывной задачи, yh – решение
приближённой разностной задачи. Предполагаем, что u(x) – непрерывная
функция.
Основной интерес: близость u(x) к yh.
1) Пространство U отображается в Uh (каждой функции u ( x) U
ставится в соответствие сеточная функция uh(x), x wh ). Обычно
uh(xi) = u(xi)
для всех xi wh . Иногда: uh(xi) – интегральное среднее значение по некоторой
окрестности данного узла xi.
2) Образуем разность
yh uh U h
Близость u(x) к yh характеризуется числом
yh uh U
h
Требуется, чтобы норма ||∙||Uh аппроксимировала норму ||∙||U в следующем
смысле:
u
u
h Uh
U
при h->0. Это условие согласованности норм.

6.

Пусть L – дифференциальный оператор, действующий на u=u(x). Заменяя в Lu
производные разностными отношениями, получим вместо Lu разностное
выражение Lhuh - линейную комбинацию значений сеточной функции uh на
некотором множестве соседних с x узлов сетки, называемых шаблоном:
Lhuh ( x) Ah ( x, )uh ( )
или
S ( x )
Lhuh ( x) i Ah ( xi , x j )uh ( x j )
x j S ( xi )
где h – шаг сетки, Ah(…) – коэффициенты, S(x) – шаблон в x. Такая
приближенная замена - разностная аппроксимация оператора L.
du
Пример.
Lu u 'x
dx
Двухточечные шаблоны:
u ( x ) u ( x h)
u ( x h) u ( x )
L hu
L hu
h
h
Можно рассмотреть линейную комбинацию:
При s=0,5:
Lshu sL h (1 s ) L h , s R
L0hu
u ( x h) u ( x h )
2h

7.

Разностная схема характеризуется понятиями:
АППРОКСИМАЦИЯ
УСТОЙЧИВОСТЬ
СХОДИМОСТЬ
Погрешностью разностной аппроксимации Lu в точке x называется
ψ(x) = Lhu(x)–Lu(x).
Lh аппроксимирует дифференциальный оператор L с порядком m>0 в точке
x, если
ψ(x) = Lhu(x)–Lu(x) = O(hm).

8.

Lu u ' ( x)
Пример.
L hu
u ( x h) u ( x )
h
По формуле Тейлора:
L hu
u ( x ) u ( x h)
h
L0hu
u ( x h) u ( x h )
2h
h2
u ( x h) u ( x) hu ' ( x) u ' ' ( x) O(h3 )
2
h2
u ( x h) u ( x) hu ' ( x) u ' ' ( x) O(h3 )
2
Получаем:
h
L hu ___________________ ( x) u ' ' ( x) O(h 2 ) O(h)
2
h
L hu __________________ ( x) u ' ' ( x) O(h 2 ) O(h)
2
L0hu ____________ 0 ( x) O(h 2 )
Т.о.,
левый и правый разностные операторы – 1-й порядок точности,
центральный разностный оператор – 2-й порядок точности.

9.

Определение.
Погрешность аппроксимации оператора L разностным
оператором Lh – сеточная функция
ψh = Lhyh–(Lu)h.
Разностный оператор Lh аппроксимирует дифференциальный оператор L,
если при h->0
h U 0
h
Разностный оператор Lh аппроксимирует дифференциальный оператор L с
порядком m>0, если
||ψh||Uh = || Lhyh–(Lu)h||Uh = O(hm)
или:
|| Lhyh–(Lu)h||Uh ≤ Mhm,
где M=const>0 не зависит от h.
Если h – вектор, под h понимается его норма (длина).

10.

Решается задача:
Lu = f,
где f – некоторая функция (правая часть).
Погрешность аппроксимации разностной схемы =
погрешность аппроксимации дифференциального оператора +
погрешность правой части ДУЧП
Lhyh=fh+δfh,
где δfh – невязка, которая для устойчивой схемы ->0 или:
|| δfh || ≤ Mhm.

11.

Ищется решение u(x,t), т.е. выделяется переменная t. Задается:
1) сетка wh в области пространства G={x=(x0,…,xn)};
2) сетка wτ на отрезке 0<=t<=t0.
Сеточная функция:
определена на сетке
y(x,t)= yh,τ(x,t)
wh,τ=wh x wτ.
Разностный оператор Lh аппроксимирует дифференциальный оператор L с
порядком m>0 по x и с порядком n>0 по t, если
||ψhτ||Uhτ=||Lhτyhτ –(Lu)hτ||Uhτ =O(hm+τn)
или
||ψhτ||Uhτ ≤ M(hm+τn),
где M=const>0 не зависит от h и τ.

12.

Меняя h, получается множество решений {yh}, зависящих от параметра h.
Выясним возможность приближения решения u задачи решением yh с любой
заданной точностью ε>0 в зависимости от шага h.
Погрешность разностной схемы:
zh = yh-uh.
Решение разностной задачи сходится, если
||zh||Uh=|| yh-uh || → 0
при h→0.
Разностная схема сходится со скоростью O(hn) или имеет n-й порядок
точности, если при достаточно малом h<h0
||zh||Uh ≤ Mhn
где M=const>0 не зависит от h.

13.

Разностная схема устойчива по входным данным ω (по правой части,
граничным, начальным условиям), если решение непрерывно зависит от
входных данных, т.е. сущ. M>0, не зависящее от h, такое что при достаточно
малом h ≤ h0
~
y ~
y
M
h
h Uh
h
h Uh
Если Lh - линеен, то устойчивость можно записать так:
1) существует (Lh)-1;
2) (Lh)-1 ограничен.
Разностная схема корректна, если
1) решение разностной задачи существует и единственно для всех входных
данных ω из некоторого допустимого семейства;
2) схема устойчива.

14.

Теорема (Филиппова). Если L линеен, разностная схема устойчива и
аппроксимирует исходную задачу, то она сходится, причем порядок точности
(скорость сходимости) определяется порядком ее аппроксимации.
Доказательство.
Пусть для Lu=f построена разностная схема Lhyh=fh.
Из аппроксимации:
|| δfh || = || Lhyh–fh || = || Lhyh– Lhuh || ≤ Mhn.
|| yh - uh ||=|| Lh-1Lhyh– Lh-1Lhuh || ≤ || Lh-1||*||Lhyh –Lhuh || ≤ M1M2hn.
(1-я константа из устойчивости, 2-я - из аппроксимации).
АППРОКСИМАЦИЯ + УСТОЙЧИВОСТЬ => СХОДИМОСТЬ
14

15.

Численные методы решений дифференциальных уравнений в
частных производных гиперболического типа
ДУЧП гиперболического типа: найти u(t,x)
2
2u
2 u
a
f (t , x)
t 2
x 2
0 x s
0 t T
Начальные условия:
u(0, x) 1 ( x)
u
u 't (0, x) (0, x) 2 ( x)
t
Граничные условия:
u(t ,0) 3 (t )
u(t , s) 4 (t )
x [0; s]
t [0;T ]

16.

Равномерная прямоугольная сетка по t, x с шагами τ и h соответственно:
ti = iτ, i=0,…,M;
xj = jh, j=0,…,N.
t
T
0
s
x

17.

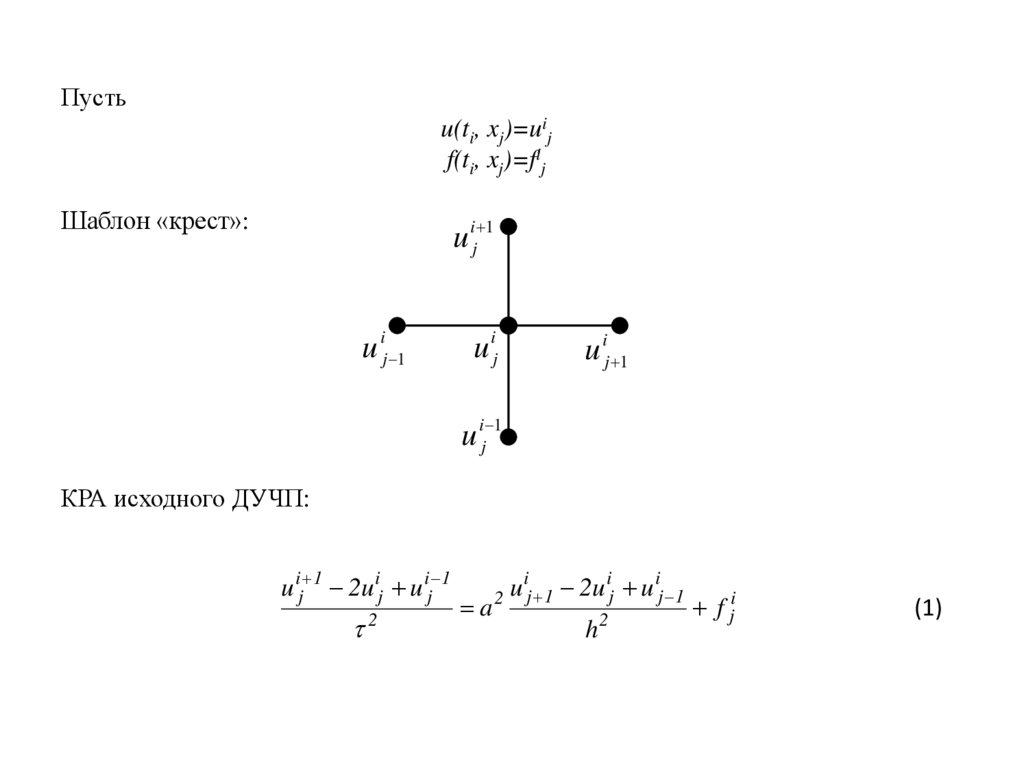
Пусть
u(ti, xj)=uij
f(ti, xj)=fij
Шаблон «крест»:
u ij 1
u ij 1
u ij
u ij 1
u ij 1
КРА исходного ДУЧП:
u ij 1 2u ij u ij 1
2
a
i
i
i
u
2
u
u
j
1
j
j 1
2
h
2
f ji
(1)

18.

Граничные условия и первое начальное условие
u(0,x)=μ1(x)
аппроксимируются точно.
Второе начальное условие
u
u 't (0, x) (0, x) 2 ( x)
t
Способ 1: точность O(τ)
u 't (0, x j )
Способ 2: точность O(τ2)
u1j u 0j
2 ( x j ), j 1, , N 1
(2а)
u u u 't (0, x j )
1
j
0
j
2
2
u ' 'tt (0, x j )
Подставляем исходное ДУЧП:
2 2 2u (0, x)
a
f
(
0
,
x
)
x
x
j
2
2
x
2 2 2 1 ( x)
0
0
u j u 't (0, x j ) a
f
x x
j
2
x 2
где 2-я производная μ1(x) заменяется КРА 2-го порядка точности
u u u 't (0, x j )
1
j
0
j
j
j
(2б)

19.

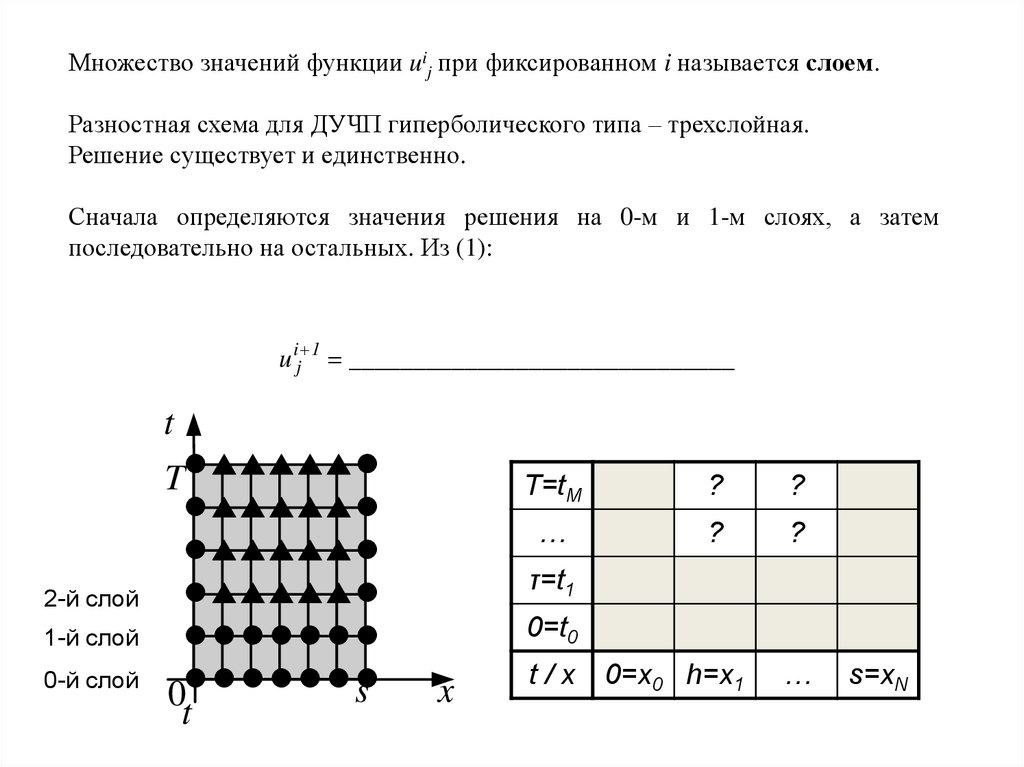
Множество значений функции uij при фиксированном i называется слоем.
Разностная схема для ДУЧП гиперболического типа – трехслойная.
Решение существует и единственно.
Сначала определяются значения решения на 0-м и 1-м слоях, а затем
последовательно на остальных. Из (1):
u ij 1 ______________________________
t
T
T=tM
?
?
…
?
?
2-й слой
τ=t1
1-й слой
0=t0
0-й слой
0
t
s
x
t/x
0=x0 h=x1
…
s=xN

20.

Аппроксимация. Разложим точное решение в (ti, xj), предполагая наличие
четвертых непрерывных производных:
u
i 1
j
u u 't
2
u ' 'tt
3
u ' ' 'ttt
4
u ' ' ' 'tttt ( 1 )
2
3!
4!
h2
h3
h4
i
u j 1 u hu ' x u ' 'xx u ' ' ' xxx u ' ' ' 'xxxx ( 2 )
2
3!
4!
Найдём невязку схемы (1):
f u ' 'tt a 2u ' ' xx
u ij 1 2u ij u ij 1
2
a
i
i
i
u
2
u
u
j
j 1
2 j 1
______________________ O( 2 h 2 )
При (2а) аппроксимация схемы O(τ2+h2).
При (2б) аппроксимация схемы O(τ+h2) - ухудшается.
h
2
...

21.

Устойчивость. Схема является условно устойчивой - при выполнении условия
Куранта,
a 1
h
Сходимость. Следует из аппроксимации и устойчивости схемы при
выполнении условия Куранта (т. Филиппова).

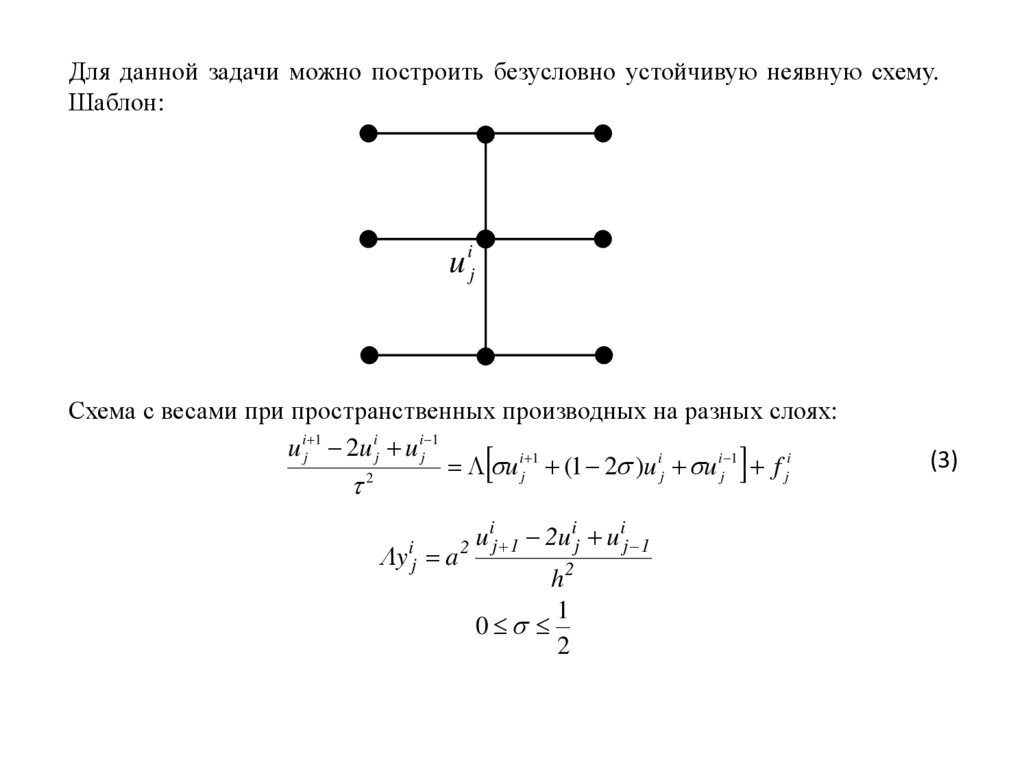
22.

Для данной задачи можно построить безусловно устойчивую неявную схему.
Шаблон:
u ij
Схема с весами при пространственных производных на разных слоях:
u ij 1 2u ij u ij 1
u ij 1 (1 2 )u ij u ij 1 f ji
2
y ij a
i
i
i
u
2
u
u
j
1
j
j 1
2
h2
1
0
2
(3)

23.

Значения на 0-м и 1-м слоях вычисляют по формулам аппроксимации 1-го
начального условия и (2б). На остальных слоях (3) с граничными условиями СЛАУ с 3-диагональной матрицей относительно yi+1j с диагональным
преобладанием. Решение этой системы существует, единственно и
вычисляется методом прогонки.
Аппроксимация: O(τ2+h2) при любом σ.
При
1
1
4
2
схема безусловно устойчива.
При
0
1
4
схема условно устойчива при
a h 1 4 2
1
При σ=0 – схема «крест», а условие устойчивости – условие Куранта.